|
Wavenumber
In the physical sciences, the wavenumber (or wave number), also known as repetency, is the spatial frequency of a wave. Ordinary wavenumber is defined as the number of wave cycles divided by length; it is a physical quantity with dimension of reciprocal length, expressed in SI units of cycles per metre or reciprocal metre (m−1). Angular wavenumber, defined as the wave phase divided by time, is a quantity with dimension of angle per length and SI units of radians per metre. They are analogous to temporal frequency, respectively the '' ordinary frequency'', defined as the number of wave cycles divided by time (in cycles per second or reciprocal seconds), and the ''angular frequency'', defined as the phase angle divided by time (in radians per second). In multidimensional systems, the wavenumber is the magnitude of the '' wave vector''. The space of wave vectors is called ''reciprocal space''. Wave numbers and wave vectors play an essential role in optics and the physics ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wave Vector
In physics, a wave vector (or wavevector) is a vector used in describing a wave, with a typical unit being cycle per metre. It has a magnitude and direction. Its magnitude is the wavenumber of the wave (inversely proportional to the wavelength), and its direction is perpendicular to the wavefront. In isotropic media, this is also the direction of wave propagation. A closely related vector is the angular wave vector (or angular wavevector), with a typical unit being radian per metre. The wave vector and angular wave vector are related by a fixed constant of proportionality, 2 radians per cycle. It is common in several fields of physics to refer to the angular wave vector simply as the ''wave vector'', in contrast to, for example, crystallography. It is also common to use the symbol for whichever is in use. In the context of special relativity, a '' wave four-vector'' can be defined, combining the (angular) wave vector and (angular) frequency. Definition The terms ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spatial Frequency
In mathematics, physics, and engineering, spatial frequency is a characteristic of any structure that is periodic across position in space. The spatial frequency is a measure of how often sinusoidal components (as determined by the Fourier transform) of the structure repeat per unit of distance. The SI unit of spatial frequency is the reciprocal metre (m−1), (11 pages) although cycle (rotational unit), cycles per (c/m) is also common. In image-processing applications, spatial freque ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reciprocal Space
Reciprocal lattice is a concept associated with solids with translational symmetry which plays a major role in many areas such as X-ray diffraction, X-ray and Electron diffraction, electron diffraction as well as the Electronic band structure, energies of electrons in a solid. It emerges from the Fourier transform of the lattice (group), lattice associated with the arrangement of the atoms. The ''direct lattice'' or ''real lattice'' is a periodic function in Space (physics), physical space, such as a crystal system (usually a Bravais lattice). The reciprocal lattice exists in the mathematical space of spatial frequencies or wavenumbers ''k'', known as reciprocal space or ''k'' space; it is the dual of physical space considered as a vector space. In other words, the reciprocal lattice is the sublattice which Dual lattice, is dual to the direct lattice. The reciprocal lattice is the set of all vector (geometric), vectors \mathbf_m, that are wave vector, wavevectors k of plane waves ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wave
In physics, mathematics, engineering, and related fields, a wave is a propagating dynamic disturbance (change from List of types of equilibrium, equilibrium) of one or more quantities. ''Periodic waves'' oscillate repeatedly about an equilibrium (resting) value at some frequency. When the entire waveform moves in one direction, it is said to be a travelling wave; by contrast, a pair of superposition principle, superimposed periodic waves traveling in opposite directions makes a ''standing wave''. In a standing wave, the amplitude of vibration has nulls at some positions where the wave amplitude appears smaller or even zero. There are two types of waves that are most commonly studied in classical physics: mechanical waves and electromagnetic waves. In a mechanical wave, Stress (mechanics), stress and Strain (mechanics), strain fields oscillate about a mechanical equilibrium. A mechanical wave is a local deformation (physics), deformation (strain) in some physical medium that propa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reduced Planck Constant
The Planck constant, or Planck's constant, denoted by h, is a fundamental physical constant of foundational importance in quantum mechanics: a photon's energy is equal to its frequency multiplied by the Planck constant, and the wavelength of a matter wave equals the Planck constant divided by the associated particle momentum. The constant was postulated by Max Planck in 1900 as a proportionality constant needed to explain experimental black-body radiation. Planck later referred to the constant as the "quantum of action". In 1905, Albert Einstein associated the "quantum" or minimal element of the energy to the electromagnetic wave itself. Max Planck received the 1918 Nobel Prize in Physics "in recognition of the services he rendered to the advancement of Physics by his discovery of energy quanta". In metrology, the Planck constant is used, together with other constants, to define the kilogram, the SI unit of mass. The SI units are defined in such a way that, when the Pla ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reciprocal Length
Reciprocal length or inverse length is a quantity or measurement used in several branches of science and mathematics, defined as the reciprocal of length. Common units used for this measurement include the reciprocal metre or inverse metre (symbol: m−1), the reciprocal centimetre or inverse centimetre (symbol: cm−1). In optics, the dioptre is a unit equivalent to reciprocal metre. List of quantities Quantities measured in reciprocal length include: * absorption coefficient or attenuation coefficient, in materials science * curvature of a line, in mathematics * gain, in laser physics * magnitude of vectors in reciprocal space, in crystallography * more generally any spatial frequency e.g. in cycles per unit length * optical power of a lens, in optics * rotational constant of a rigid rotor, in quantum mechanics * wavenumber, or magnitude of a wavevector, in spectroscopy * density of a linear feature in hydrology and other fields; see kilometre per square kil ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Neutron Diffraction
Neutron diffraction or elastic neutron scattering is the application of neutron scattering to the determination of the atomic and/or magnetic structure of a material. A sample to be examined is placed in a beam of Neutron temperature, thermal or cold neutron radiation, neutrons to obtain a diffraction pattern that provides information of the structure of the material. The technique is similar to X-ray diffraction but due to their different scattering properties, neutrons and X-rays provide complementary information: X-Rays are suited for superficial analysis, strong x-rays from synchrotron radiation are suited for shallow depths or thin specimens, while neutrons having high penetration depth are suited for bulk samples.Measurement of residual stress in materials using neutrons IAEA, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Optics
Optics is the branch of physics that studies the behaviour and properties of light, including its interactions with matter and the construction of optical instruments, instruments that use or Photodetector, detect it. Optics usually describes the behaviour of visible light, visible, ultraviolet, and infrared light. Light is a type of electromagnetic radiation, and other forms of electromagnetic radiation such as X-rays, microwaves, and radio waves exhibit similar properties. Most optical phenomena can be accounted for by using the Classical electromagnetism, classical electromagnetic description of light, however complete electromagnetic descriptions of light are often difficult to apply in practice. Practical optics is usually done using simplified models. The most common of these, geometric optics, treats light as a collection of Ray (optics), rays that travel in straight lines and bend when they pass through or reflect from surfaces. Physical optics is a more comprehensive mo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scattering
In physics, scattering is a wide range of physical processes where moving particles or radiation of some form, such as light or sound, are forced to deviate from a straight trajectory by localized non-uniformities (including particles and radiation) in the medium through which they pass. In conventional use, this also includes deviation of reflected radiation from the angle predicted by the law of reflection. Reflections of radiation that undergo scattering are often called ''diffuse reflections'' and unscattered reflections are called ''specular'' (mirror-like) reflections. Originally, the term was confined to light scattering (going back at least as far as Isaac Newton in the 17th century). As more "ray"-like phenomena were discovered, the idea of scattering was extended to them, so that William Herschel could refer to the scattering of "heat rays" (not then recognized as electromagnetic in nature) in 1800. John Tyndall, a pioneer in light scattering research, noted the connecti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
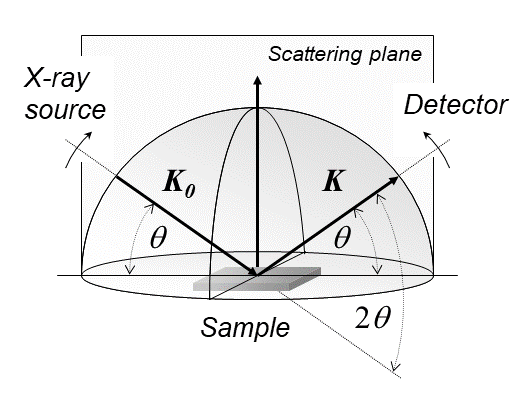
X-ray Diffraction
X-ray diffraction is a generic term for phenomena associated with changes in the direction of X-ray beams due to interactions with the electrons around atoms. It occurs due to elastic scattering, when there is no change in the energy of the waves. The resulting map of the directions of the X-rays far from the sample is called a diffraction pattern. It is different from X-ray crystallography which exploits X-ray diffraction to determine the arrangement of atoms in materials, and also has other components such as ways to map from experimental diffraction measurements to the positions of atoms. This article provides an overview of X-ray diffraction, starting with the early #History, history of x-rays and the discovery that they have the right spacings to be diffracted by crystals. In many cases these diffraction patterns can be #Introduction to x-ray diffraction theory, Interpreted using a single scattering or kinematical theory with conservation of energy (#Ewald's sphere, wave vecto ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Commutative Diagram Of Harmonic Wave Properties
In mathematics, a binary operation is commutative if changing the order of the operands does not change the result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it. Perhaps most familiar as a property of arithmetic, e.g. or , the property can also be used in more advanced settings. The name is needed because there are operations, such as division (mathematics), division and subtraction, that do not have it (for example, ); such operations are ''not'' commutative, and so are referred to as noncommutative operations. The idea that simple operations, such as the multiplication (mathematics), multiplication and addition of numbers, are commutative was for many centuries implicitly assumed. Thus, this property was not named until the 19th century, when new algebraic structures started to be studied. Definition A binary operation * on a Set (mathematics), set ''S'' is ''commutative'' if x * y = y * x for all x,y \in S. An operat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electron Diffraction
Electron diffraction is a generic term for phenomena associated with changes in the direction of electron beams due to elastic interactions with atoms. It occurs due to elastic scattering, when there is no change in the energy of the electrons. The negatively charged electrons are scattered due to Coulomb forces when they interact with both the positively charged atomic core and the negatively charged electrons around the atoms. The resulting map of the directions of the electrons far from the sample is called a diffraction pattern, see for instance Figure 1. Beyond patterns showing the directions of electrons, electron diffraction also plays a major role in the contrast of images in electron microscopes. This article provides an overview of electron diffraction and electron diffraction patterns, collective referred to by the generic name electron diffraction. This includes aspects of how in a general way electrons can act as waves, and diffract and interact with matter. It a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |