Reciprocal space

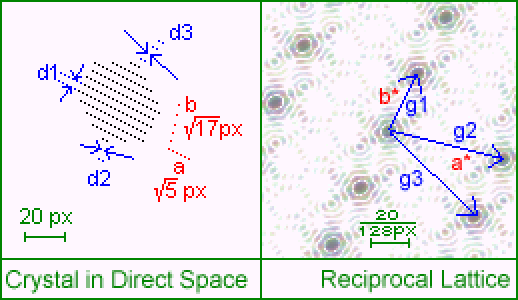Reciprocal lattice is a concept associated with solids with translational symmetry which plays a major role in many areas such as X-ray and electron diffraction as well as the energies of electrons in a solid. It emerges from the Fourier transform of the lattice associated with the arrangement of the atoms. The ''direct lattice'' or ''real lattice'' is a periodic function in physical space, such as a crystal system (usually a Bravais lattice). The reciprocal lattice exists in the mathematical space of spatial frequencies or wavenumbers ''k'', known as reciprocal space or ''k'' space; it is the dual of physical space considered as a vector space. In other words, the reciprocal lattice is the sublattice which is dual to the direct lattice.

The reciprocal lattice is the set of all vectors $\mathbf_m$, that are wavevectors k of plane waves in the Fourier series of a spatial function whose periodicity is the same as that of a direct lattice $\mathbf_n$. Each plane wave in this Fourier series has the same phase or phases that are differed by multiples of $2\pi$, at each direct lattice point (so essentially same phase at all the direct lattice points).

The reciprocal lattice of a reciprocal lattice is equivalent to the original direct lattice, because the defining equations are symmetrical with respect to the vectors in real and reciprocal space. Mathematically, direct and reciprocal lattice vectors represent covariant and contravariant vectors, respectively.

The Brillouin zone is a Wigner–Seitz cell of the reciprocal lattice.

Wave-based description

Reciprocal space

Reciprocal space (also called -space) provides a way to visualize the results of the Fourier transform of a spatial function. It is similar in role to the frequency domain arising from the Fourier transform of a time dependent function; reciprocal space is a space over which the Fourier transform of a spatial function is represented at spatial frequencies or wavevectors of plane waves of the Fourier transform. The domain of the spatial function itself is often referred to as spatial domain or real space. In physical applications, such as crystallography, both real and reciprocal space will often each be two or three dimensional. Whereas the number of spatial dimensions of these two associated spaces will be the same, the spaces will differ in their quantity dimension, so that when the real space has the dimension length (L), its reciprocal space will have inverse length, so L⁻¹ (the reciprocal of length).

Reciprocal space comes into play regarding waves, both classical and quantum mechanical. Because a sinusoidal plane wave with unit amplitude can be written as an oscillatory term $\cos(kx - \omega t + \varphi_0)$, with initial phase $\varphi_0$, angular wavenumber $k$ and angular frequency $\omega$, it can be regarded as a function of both $k$ and $x$ (and the time-varying part as a function of both $\omega$ and $t$). This complementary role of $k$ and $x$ leads to their visualization within complementary spaces (the real space and the reciprocal space). The spatial periodicity of this wave is defined by its wavelength $\lambda$, where $k \lambda = 2\pi$; hence the corresponding wavenumber in reciprocal space will be $k = 2\pi / \lambda$.

In three dimensions, the corresponding plane wave term becomes $\cos(\mathbf \cdot \mathbf - \omega t + \varphi_0)$, which simplifies to $\cos(\mathbf \cdot \mathbf + \varphi)$ at a fixed time $t$, where $\mathbf$ is the position vector of a point in real space and now $\mathbf=2\pi \mathbf / \lambda$ is the wavevector in the three dimensional reciprocal space. (The magnitude of a wavevector is called wavenumber.) The constant $\varphi$ is the phase of the wavefront (a plane of a constant phase) through the origin $\mathbf=0$ at time $t$, and $\mathbf$ is a unit normal vector to this wavefront. The wavefronts with phases $\varphi + (2\pi)n$, where $n$ represents any integer, comprise a set of parallel planes, equally spaced by the wavelength $\lambda$.

Reciprocal lattice

In general, a geometric lattice is an infinite, regular array of vertices (points) in space, which can be modelled vectorially as a Bravais lattice. Some lattices may be skew, which means that their primary lines may not necessarily be at right angles. In reciprocal space, a reciprocal lattice is defined as the set of wavevectors $\mathbf$ of plane waves in the Fourier series of any function $f(\mathbf)$ whose periodicity is compatible with that of an initial direct lattice in real space. Equivalently, a wavevector is a vertex of the reciprocal lattice if it corresponds to a plane wave in real space whose phase at any given time is the same (actually differs by $(2\pi)n$ with an integer $n$) at every direct lattice vertex.

One heuristic approach to constructing the reciprocal lattice in three dimensions is to write the position vector of a vertex of the direct lattice as $\mathbf = n_1\mathbf_1 + n_2\mathbf_2 + n_3\mathbf_3$, where the $n_i$ are integers defining the vertex and the $\mathbf_i$ are linearly independent primitive translation vectors (or shortly called primitive vectors) that are characteristic of the lattice. There is then a unique plane wave (up to a factor of negative one), whose wavefront through the origin $\mathbf = 0$ contains the direct lattice points at $\mathbf_2$ and $\mathbf_3$, and with its adjacent wavefront (whose phase differs by $2\pi$ or $-2\pi$ from the former wavefront passing the origin) passing through $\mathbf_1$. Its angular wavevector takes the form $\mathbf_1 = 2\pi \mathbf_1 / \lambda_$, where $\mathbf_1$ is the unit vector perpendicular to these two adjacent wavefronts and the wavelength $\lambda_1$ must satisfy $\lambda_1 = \mathbf_1 \cdot \mathbf_1$, means that $\lambda_1$ is equal to the distance between the two wavefronts. Hence by construction $\mathbf_1 \cdot \mathbf_1 = 2\pi$ and $\mathbf_2 \cdot \mathbf_1 = \mathbf_3 \cdot \mathbf_1 = 0$.

Cycling through the indices in turn, the same method yields three wavevectors $\mathbf_j$ with $\mathbf_i \cdot \mathbf_j = 2\pi \, \delta_$, where the Kronecker delta $\delta_$ equals one when $i=j$ and is zero otherwise. The $\mathbf_j$ comprise a set of three primitive wavevectors or three primitive translation vectors for the reciprocal lattice, each of whose vertices takes the form $\mathbf = m_1\mathbf_1 + m_2\mathbf_2 + m_3\mathbf_3$, where the $m_j$ are integers. The reciprocal lattice is also a Bravais lattice as it is formed by integer combinations of the primitive vectors, that are $\mathbf_1$, $\mathbf_2$, and $\mathbf_3$ in this case. Simple algebra then shows that, for any plane wave with a wavevector $\mathbf$ on the reciprocal lattice, the total phase shift $\mathbf \cdot \mathbf$ between the origin and any point $\mathbf$ on the direct lattice is a multiple of $2\pi$ (that can be possibly zero if the multiplier is zero), so the phase of the plane wave with $\mathbf$ will essentially be equal for every direct lattice vertex, in conformity with the reciprocal lattice definition above. (Although any wavevector $\mathbf$ on the reciprocal lattice does always take this form, this derivation is motivational, rather than rigorous, because it has omitted the proof that no other possibilities exist.)

The Brillouin zone is a primitive cell (more specifically a Wigner–Seitz cell) of the reciprocal lattice, which plays an important role in solid state physics due to Bloch's theorem. In pure mathematics, the dual space of linear forms and the dual lattice provide more abstract generalizations of reciprocal space and the reciprocal lattice.

Mathematical description

Assuming a three-dimensional Bravais lattice and labelling each lattice vector (a vector indicating a lattice point) by the subscript $n = (n_1, n_2, n_3)$ as 3-tuple of integers,

:$\mathbf_n = n_1 \mathbf_1 + n_2 \mathbf_2 + n_3 \mathbf_3$ where $n_1, n_2, n_3 \in \mathbb$

where $\mathbb$ is the set of integers and $\mathbf_i$ is a primitive translation vector or shortly primitive vector. Taking a function $f(\mathbf)$ where $\mathbf$ is a position vector from the origin $\mathbf_n = 0$ to any position, if $f(\mathbf)$ follows the periodicity of this lattice, e.g. the function describing the electronic density in an atomic crystal, it is useful to write $f(\mathbf)$ as a multi-dimensional Fourier series

:$\sum_m f_m e^ = f\left(\mathbf\right)$

where now the subscript $m = (m_1, m_2, m_3)$, so this is a triple sum.

As $f(\mathbf)$ follows the periodicity of the lattice, translating $\mathbf$ by any lattice vector $\mathbf_n$ we get the same value, hence

:$f(\mathbf + \mathbf_n) = f(\mathbf).$

Expressing the above instead in terms of their Fourier series we have
$\sum_m f_m e^ = \sum_m f_m e^ = \sum_m f_m e^ \, e^.$

Because equality of two Fourier series implies equality of their coefficients, $e^ = 1$, which only holds when

:$\mathbf_m \cdot \mathbf_n = 2\pi N$ where $N \in \mathbb.$

Mathematically, the reciprocal lattice is the set of all vectors $\mathbf_m$, that are wavevectors of plane waves in the Fourier series of a spatial function whose periodicity is the same as that of a direct lattice as the set of all direct lattice point position vectors $\mathbf_n$, and $\mathbf_m$ satisfy this equality for all $\mathbf_n$. Each plane wave in the Fourier series has the same phase (actually can be differed by a multiple of $2\pi$) at all the lattice point $\mathbf_n$.

As shown in the section multi-dimensional Fourier series, $\mathbf_m$ can be chosen in the form of $\mathbf_m = m_1 \mathbf_1 + m_2 \mathbf_2 + m_3 \mathbf_3$ where $\mathbf_i \cdot \mathbf_j = 2\pi \, \delta_$. With this form, the reciprocal lattice as the set of all wavevectors $\mathbf_m$ for the Fourier series of a spatial function which periodicity follows $\mathbf_n$, is itself a Bravais lattice as it is formed by integer combinations of its own primitive translation vectors $\left(\mathbf, \mathbf_2, \mathbf_3\right)$, and the reciprocal of the reciprocal lattice is the original lattice, which reveals the Pontryagin duality of their respective vector spaces. (There may be other form of $\mathbf_m$. Any valid form of $\mathbf_m$ results in the same reciprocal lattice.)

Two dimensions

For an infinite two-dimensional lattice, defined by its primitive vectors $\left(\mathbf_1, \mathbf_2\right)$, its reciprocal lattice can be determined by generating its two reciprocal primitive vectors, through the following formulae,

:$\mathbf_m = m_1 \mathbf_1 + m_2 \mathbf_2$

where $m_i$ is an integer and

:\begin
\mathbf_1 &= 2\pi \frac = 2\pi \frac \\ pt \mathbf_2 &= 2\pi \frac
\end

Here $\mathbf$ represents a 90 degree rotation matrix, i.e. a ''q''uarter turn. The anti-clockwise rotation and the clockwise rotation can both be used to determine the reciprocal lattice: If $\mathbf$ is the anti-clockwise rotation and $\mathbf$ is the clockwise rotation, $\mathbf\,\mathbf=-\mathbf\,\mathbf$ for all vectors $\mathbf$. Thus, using the permutation
: $\sigma = \begin 1 & 2 \\ 2 & 1 \end$
we obtain
:$\mathbf_n = 2\pi \frac=2\pi \frac.$

Notably, in a 3D space this 2D reciprocal lattice is an infinitely extended set of Bragg rods—described by Sung et al.

Three dimensions

For an infinite three-dimensional lattice $\mathbf_n = n_1 \mathbf_1 + n_2 \mathbf_2 + n_3 \mathbf_3$, defined by its primitive vectors $\left(\mathbf, \mathbf_2, \mathbf_3\right)$ and the subscript of integers $n = \left( n_1, n_2, n_3 \right)$, its reciprocal lattice $\mathbf_m = m_1 \mathbf_1 + m_2 \mathbf_2 + m_3 \mathbf_3$ with the integer subscript $m = (m_1, m_2, m_3)$ can be determined by generating its three reciprocal primitive vectors $\left(\mathbf, \mathbf_2, \mathbf_3\right)$
\begin
\mathbf_1 &= \frac \ \mathbf_2 \times \mathbf_3 \\ pt \mathbf_2 &= \frac \ \mathbf_3 \times \mathbf_1 \\ pt \mathbf_3 &= \frac \ \mathbf_1 \times \mathbf_2
\end
where $V = \mathbf_1 \cdot \left(\mathbf_2 \times \mathbf_3\right) = \mathbf_2 \cdot \left(\mathbf_3 \times \mathbf_1\right) = \mathbf_3 \cdot \left(\mathbf_1 \times \mathbf_2\right)$ is the scalar triple product. The choice of these $\left(\mathbf, \mathbf_2, \mathbf_3\right)$ is to satisfy $\mathbf_i \cdot \mathbf_j = 2\pi \, \delta_$ as the known condition (There may be other condition.) of primitive translation vectors for the reciprocal lattice derived in the heuristic approach above and the section multi-dimensional Fourier series. This choice also satisfies the requirement of the reciprocal lattice $e^ = 1$ mathematically derived above. Using column vector representation of (reciprocal) primitive vectors, the formulae above can be rewritten using matrix inversion:

:\left mathbf_1\mathbf_2\mathbf_3\right\mathsf = 2\pi\left mathbf_1\mathbf_2\mathbf_3\right.

This method appeals to the definition, and allows generalization to arbitrary dimensions. The cross product formula dominates introductory materials on crystallography.

The above definition is called the "physics" definition, as the factor of $2 \pi$ comes naturally from the study of periodic structures. An essentially equivalent definition, the "crystallographer's" definition, comes from defining the reciprocal lattice $\mathbf_m = \mathbf_m / 2\pi$. which changes the reciprocal primitive vectors to be

:$\mathbf_1 = \frac$
and so on for the other primitive vectors. The crystallographer's definition has the advantage that the definition of $\mathbf_1$ is just the reciprocal magnitude of $\mathbf_1$ in the direction of $\mathbf_2 \times \mathbf_3$, dropping the factor of $2 \pi$. This can simplify certain mathematical manipulations, and expresses reciprocal lattice dimensions in units of spatial frequency. It is a matter of taste which definition of the lattice is used, as long as the two are not mixed.

$m = (m_1, m_2, m_3)$ is conventionally written as $(h, k, \ell)$ or $(hk\ell)$, called Miller indices; $m_1$ is replaced with $h$, $m_2$ replaced with $k$, and $m_3$ replaced with $\ell$. Each lattice point $(hk\ell)$ in the reciprocal lattice corresponds to a set of lattice planes $(hk\ell)$ in the real space lattice. (A lattice plane is a plane crossing lattice points.) The direction of the reciprocal lattice vector corresponds to the normal to the real space planes. The magnitude of the reciprocal lattice vector $\mathbf_m$ is given in reciprocal length and is equal to the reciprocal of the interplanar spacing of the real space planes.

Higher dimensions

The formula for $n$ dimensions can be derived assuming an $n$-dimensional real vector space $V$ with a basis $(\mathbf_1,\ldots,\mathbf_n)$ and an inner product $g\colon V\times V\to\mathbf$. The reciprocal lattice vectors are uniquely determined by the formula $g(\mathbf_i,\mathbf_j)=2\pi\delta_$. Using the permutation
: $\sigma = \begin 1 & 2 & \cdots &n\\ 2 & 3 & \cdots &1 \end,$
they can be determined with the following formula:
:$\mathbf_i = 2\pi\fracg^(\mathbf_\,\lrcorner\ldots\mathbf_\,\lrcorner\,\omega)\in V$
Here, $\omega\colon V^n \to \mathbf$ is the volume form, $g^$ is the inverse of the vector space isomorphism $\hat\colon V \to V^*$ defined by $\hat(v)(w) = g(v,w)$ and $\lrcorner$ denotes the inner multiplication.

One can verify that this formula is equivalent to the known formulas for the two- and three-dimensional case by using the following facts: In three dimensions, $\omega(u,v,w) = g(u \times v, w)$ and in two dimensions, $\omega(v,w) = g(Rv,w)$, where $R \in \text(2) \subset L(V,V)$ is the rotation by 90 degrees (just like the volume form, the angle assigned to a rotation depends on the choice of orientation).

Reciprocal lattices of various crystals

Reciprocal lattices for the cubic crystal system are as follows.

Simple cubic lattice

The simple cubic Bravais lattice, with cubic primitive cell of side $a$, has for its reciprocal a simple cubic lattice with a cubic primitive cell of side $\frac$ (or $\frac$ in the crystallographer's definition). The cubic lattice is therefore said to be self-dual, having the same symmetry in reciprocal space as in real space.

Face-centered cubic (FCC) lattice

The reciprocal lattice to an FCC lattice is the body-centered cubic (BCC) lattice, with a cube side of $\frac$.

Consider an FCC compound unit cell. Locate a primitive unit cell of the FCC; i.e., a unit cell with one lattice point. Now take one of the vertices of the primitive unit cell as the origin. Give the basis vectors of the real lattice. Then from the known formulae, you can calculate the basis vectors of the reciprocal lattice. These reciprocal lattice vectors of the FCC represent the basis vectors of a BCC real lattice. The basis vectors of a real BCC lattice and the reciprocal lattice of an FCC resemble each other in direction but not in magnitude.

Body-centered cubic (BCC) lattice

The reciprocal lattice to a BCC lattice is the FCC lattice, with a cube side of $4\pi/a$.

It can be proven that only the Bravais lattices which have 90 degrees between $\left(\mathbf_1, \mathbf_2, \mathbf_3\right)$ (cubic, tetragonal, orthorhombic) have primitive translation vectors for the reciprocal lattice, $\left(\mathbf_1, \mathbf_2, \mathbf_3\right)$, parallel to their real-space vectors.

Simple hexagonal lattice

The reciprocal to a simple hexagonal Bravais lattice with lattice constants $a$ and $c$ is another simple hexagonal lattice with lattice constants $2\pi/c$ and $4\pi/(a\sqrt3)$ rotated through 90° about the ''c'' axis with respect to the direct lattice. The simple hexagonal lattice is therefore said to be self-dual, having the same symmetry in reciprocal space as in real space. Primitive translation vectors for this simple hexagonal Bravais lattice vectors are

\begin
a_1 & = \frac a \hat + \frac a \hat, \\ pta_2 & = - \frac a \hat + \fraca\hat, \\ pta_3 & = c \hat.
\end

Arbitrary collection of atoms

One path to the reciprocal lattice of an arbitrary collection of atoms comes from the idea of scattered waves in the Fraunhofer (long-distance or lens back-focal-plane) limit as a Huygens-style sum of amplitudes from all points of scattering (in this case from each individual atom).B. E. Warren (1969/1990) ''X-ray diffraction'' (Addison-Wesley, Reading MA/Dover, Mineola NY). This sum is denoted by the complex amplitude $F$ in the equation below, because it is also the Fourier transform (as a function of spatial frequency or reciprocal distance) of an effective scattering potential in direct space:

:F vec= \sum_^N f_j\!\left vec\righte^.

Here g = q/(2) is the scattering vector q in crystallographer units, ''N'' is the number of atoms, ''f''_''j'' ''gis the atomic scattering factor for atom ''j'' and scattering vector g, while r_''j'' is the vector position of atom ''j''. The Fourier phase depends on one's choice of coordinate origin.

For the special case of an infinite periodic crystal, the scattered amplitude ''F'' = ''M'' ''F_h,k,ℓ'' from ''M'' unit cells (as in the cases above) turns out to be non-zero only for integer values of $(h,k,\ell)$, where

:F_ = \sum_^m f_j\left _\righte^

when there are ''j'' = 1,''m'' atoms inside the unit cell whose fractional lattice indices are respectively . To consider effects due to finite crystal size, of course, a shape convolution for each point or the equation above for a finite lattice must be used instead.

Whether the array of atoms is finite or infinite, one can also imagine an "intensity reciprocal lattice" I ''g which relates to the amplitude lattice F via the usual relation ''I'' = ''F''^*''F'' where ''F''^* is the complex conjugate of F. Since Fourier transformation is reversible, of course, this act of conversion to intensity tosses out "all except 2nd moment" (i.e. the phase) information. For the case of an arbitrary collection of atoms, the intensity reciprocal lattice is therefore:

:I vec= \sum_^N \sum_^N f_j \left vec\rightf_k \left vec\righte^.

Here r_''jk'' is the vector separation between atom ''j'' and atom ''k''. One can also use this to predict the effect of nano-crystallite shape, and subtle changes in beam orientation, on detected diffraction peaks even if in some directions the cluster is only one atom thick. On the down side, scattering calculations using the reciprocal lattice basically consider an incident plane wave. Thus after a first look at reciprocal lattice (kinematic scattering) effects, beam broadening and multiple scattering (i.e. dynamical) effects may be important to consider as well.

Generalization of a dual lattice

There are actually two versions in mathematics of the abstract dual lattice concept, for a given lattice ''L'' in a real vector space ''V'', of finite dimension.

The first, which generalises directly the reciprocal lattice construction, uses Fourier analysis. It may be stated simply in terms of Pontryagin duality. The dual group ''V''^ to ''V'' is again a real vector space, and its closed subgroup ''L''^ dual to ''L'' turns out to be a lattice in ''V''^. Therefore, ''L''^ is the natural candidate for ''dual lattice'', in a different vector space (of the same dimension).

The other aspect is seen in the presence of a quadratic form ''Q'' on ''V''; if it is non-degenerate it allows an identification of the dual space ''V''^* of ''V'' with ''V''. The relation of ''V''^* to ''V'' is not intrinsic; it depends on a choice of Haar measure (volume element) on ''V''. But given an identification of the two, which is in any case well-defined up to a scalar, the presence of ''Q'' allows one to speak to the dual lattice to ''L'' while staying within ''V''.

In mathematics, the dual lattice of a given lattice ''L'' in an abelian locally compact topological group ''G'' is the subgroup ''L''^∗ of the dual group of ''G'' consisting of all continuous characters that are equal to one at each point of ''L''.

In discrete mathematics, a lattice is a locally discrete set of points described by all integral linear combinations of linearly independent vectors in R^''n''. The dual lattice is then defined by all points in the linear span of the original lattice (typically all of R^''n'') with the property that an integer results from the inner product with all elements of the original lattice. It follows that the dual of the dual lattice is the original lattice.

Furthermore, if we allow the matrix ''B'' to have columns as the linearly independent vectors that describe the lattice, then the matrix $A = B\left(B^\mathsf B\right)^$ has columns of vectors that describe the dual lattice.

In quantum physics

In quantum physics, reciprocal space is closely related to '' momentum space'' according to the proportionality $\mathbf = \hbar \mathbf$, where $\mathbf$ is the momentum vector and $\hbar$ is the reduced Planck constant.

See also

*
*
*
*
*
*
*
*

References

External links

* http://newton.umsl.edu/run//nano/known.html – Jmol-based electron diffraction simulator lets you explore the intersection between reciprocal lattice and Ewald sphere during tilt.

DoITPoMS Teaching and Learning Package on Reciprocal Space and the Reciprocal Lattice

{{DEFAULTSORT:Reciprocal Lattice
Crystallography
Fourier analysis
Lattice points
Neutron-related techniques
Synchrotron-related techniques
Diffraction
Condensed matter physics