|
Repetition Code
In coding theory, the repetition code is one of the most basic linear error-correcting codes. In order to transmit a message over a noisy channel that may corrupt the transmission in a few places, the idea of the repetition code is to just repeat the message several times. The hope is that the channel corrupts only a minority of these repetitions. This way the receiver will notice that a transmission error occurred since the received data stream is not the repetition of a single message, and moreover, the receiver can recover the original message by looking at the received message in the data stream that occurs most often. Because of the bad error correcting performance coupled with the low code rate (ratio between useful information symbols and actual transmitted symbols), other error correction codes are preferred in most cases. The chief attraction of the repetition code is the ease of implementation. Code parameters In the case of a binary repetition code, there exist two co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coding Theory
Coding theory is the study of the properties of codes and their respective fitness for specific applications. Codes are used for data compression, cryptography, error detection and correction, data transmission and computer data storage, data storage. Codes are studied by various scientific disciplines—such as information theory, electrical engineering, mathematics, linguistics, and computer science—for the purpose of designing efficient and reliable data transmission methods. This typically involves the removal of redundancy and the correction or detection of errors in the transmitted data. There are four types of coding: # Data compression (or ''source coding'') # Error detection and correction, Error control (or ''channel coding'') # Cryptography, Cryptographic coding # Line code, Line coding Data compression attempts to remove unwanted redundancy from the data from a source in order to transmit it more efficiently. For example, DEFLATE data compression makes files small ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Block Code
In coding theory, block codes are a large and important family of Channel coding, error-correcting codes that encode data in blocks. There is a vast number of examples for block codes, many of which have a wide range of practical applications. The abstract definition of block codes is conceptually useful because it allows coding theorists, mathematicians, and computer scientists to study the limitations of ''all'' block codes in a unified way. Such limitations often take the form of ''bounds'' that relate different parameters of the block code to each other, such as its rate and its ability to detect and correct errors. Examples of block codes are Reed–Solomon codes, Hamming codes, Hadamard codes, Expander codes, Golay code (other), Golay codes, Reed–Muller codes and Polar code (coding theory), Polar codes. These examples also belong to the class of linear codes, and hence they are called linear block codes. More particularly, these codes are known as algebraic block ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
FlexRay
FlexRay is an automotive network communications protocol developed by the FlexRay Consortium to govern on-board automotive computing. It is designed to be faster and more reliable than CAN and TTP, but it is also more expensive. The FlexRay consortium disbanded in 2009, but the FlexRay standard is now a set of ISO standards, ISO 17458-1 to 17458-5. FlexRay is a communication bus designed to ensure high data rates, fault tolerance, operating on a time cycle, split into static and dynamic segments for event-triggered and time-triggered communications. It is mainly used in aeronautic and automotive sectors. Features FlexRay supports data rates up to , explicitly supports both star and bus physical topologies, and can have two independent data channels for fault-tolerance (communication can continue with reduced bandwidth if one channel is inoperative). The bus operates on a time cycle, divided into two parts: the static segment and the dynamic segment. The static segment is preal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
UART
A universal asynchronous receiver-transmitter (UART ) is a peripheral device for asynchronous serial communication in which the data format and transmission speeds are configurable. It sends data bits one by one, from the least significant to the most significant, framed by start and stop bits so that precise timing is handled by the communication channel. The electric signaling levels are handled by a driver circuit external to the UART. Common signal levels are RS-232, RS-485, and raw TTL for short debugging links. Early teletypewriters used current loops. It was one of the earliest computer communication devices, used to attach teletypewriters for an operator console. It was also an early hardware system for the Internet. A UART is usually implemented in an integrated circuit (IC) and used for serial communications over a computer or peripheral device serial port. One or more UART peripherals are commonly integrated in microcontroller chips. Specialised UARTs are used ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fountain Code
In coding theory, fountain codes (also known as rateless erasure codes) are a class of erasure codes with the property that a potentially limitless sequence of encoding symbols can be generated from a given set of source symbols such that the original source symbols can ideally be recovered from any subset of the encoding symbols of size equal to or only slightly larger than the number of source symbols. The term ''fountain'' or ''rateless'' refers to the fact that these codes do not exhibit a fixed code rate. A fountain code is optimal if the original ''k'' source symbols can be recovered from any ''k'' successfully received encoding symbols (i.e., excluding those that were erased). Fountain codes are known that have efficient encoding and decoding algorithms and that allow the recovery of the original ''k'' source symbols from any ''k’'' of the encoding symbols with high probability, where ''k’'' is just slightly larger than ''k''. LT codes were the first practical realizat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binary Erasure Channel
In coding theory and information theory, a binary erasure channel (BEC) is a communications channel model. A transmitter sends a bit (a zero or a one), and the receiver either receives the bit correctly, or with some probability P_e receives a message that the bit was not received ("erased") . Definition A binary erasure channel with erasure probability P_e is a channel with binary input, ternary output, and probability of erasure P_e. That is, let X be the transmitted random variable with alphabet \. Let Y be the received variable with alphabet \, where \text is the erasure symbol. Then, the channel is characterized by the conditional probabilities: :\begin \operatorname X = 0 &= 1 - P_e \\ \operatorname X = 1 &= 0 \\ \operatorname X = 0 &= 0 \\ \operatorname X = 1 &= 1 - P_e \\ \operatorname X = 0 &= P_e \\ \operatorname X = 1 &= P_e \end Capacity The channel capacity of a BEC is 1-P_e, attained with a uniform distribution for X (i.e. half of the inputs ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
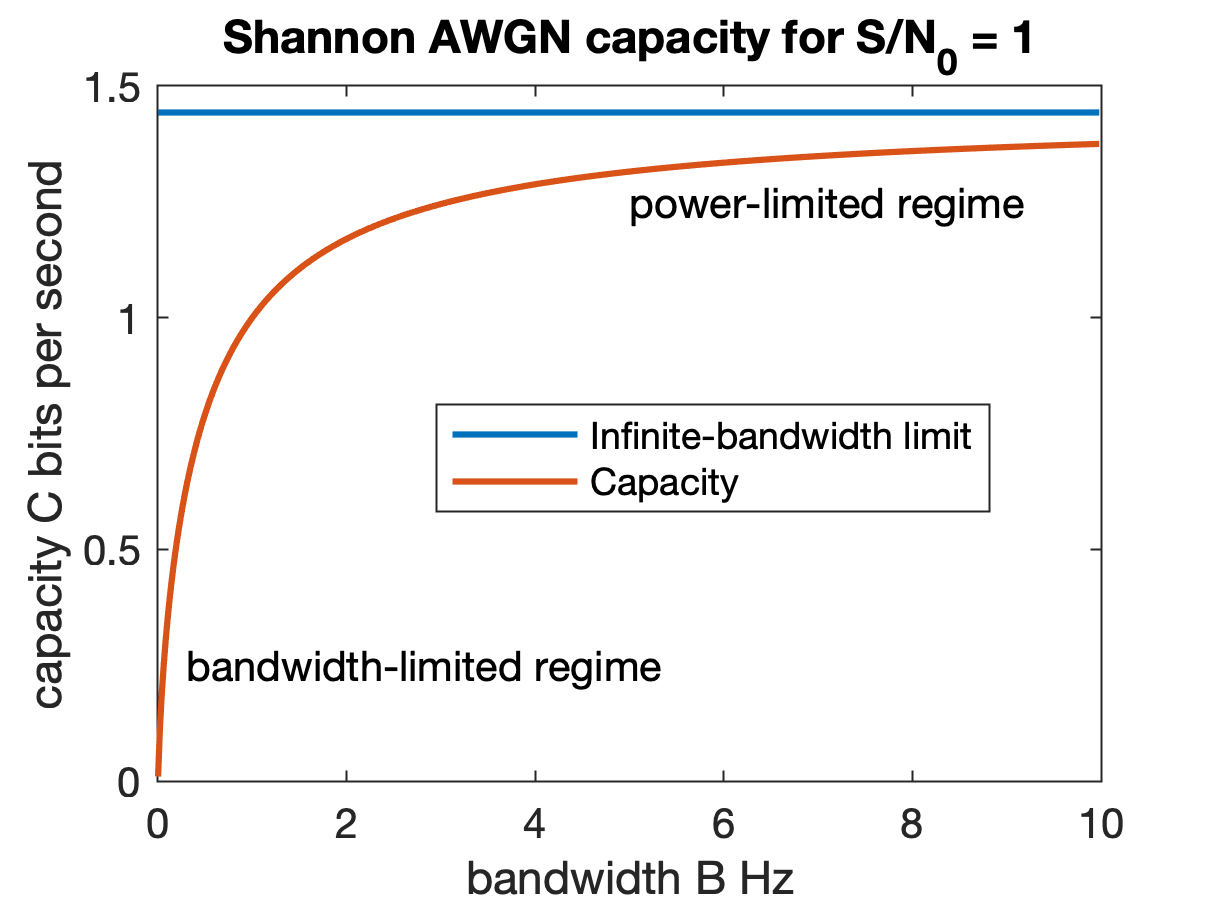
Channel Capacity
Channel capacity, in electrical engineering, computer science, and information theory, is the theoretical maximum rate at which information can be reliably transmitted over a communication channel. Following the terms of the noisy-channel coding theorem, the channel capacity of a given Channel (communications), channel is the highest information rate (in units of information entropy, information per unit time) that can be achieved with arbitrarily small error probability. Information theory, developed by Claude E. Shannon in 1948, defines the notion of channel capacity and provides a mathematical model by which it may be computed. The key result states that the capacity of the channel, as defined above, is given by the maximum of the mutual information between the input and output of the channel, where the maximization is with respect to the input distribution. The notion of channel capacity has been central to the development of modern wireline and wireless communication system ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Repeat-accumulate Code
In computer science, repeat-accumulate codes (RA codes) are a low complexity class of error-correcting codes. They were devised so that their ensemble weight distributions are easy to derive. RA codes were introduced by Divsalar ''et al.'' In an RA code, an information block of length is repeated times, scrambled by an interleaver of size , and then encoded by a rate 1 accumulator. The accumulator can be viewed as a truncated rate 1 recursive convolutional encoder with transfer function , but Divsalar ''et al.'' prefer to think of it as a block code whose input block and output block are related by the formula and x_i = x_+z_i for i > 1. The encoding time for RA codes is linear and their rate is 1/q. They are nonsystematic. Irregular repeat accumulate codes Irregular repeat accumulate (IRA) codes build on top of the ideas of RA codes. IRA replaces the outer code in RA code with a low density generator matrix code. IRA codes first repeats information bits different time ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Concatenated Error Correction Codes
In coding theory, concatenated codes form a class of error-correcting codes that are derived by combining an inner code and an outer code. They were conceived in 1966 by Dave Forney as a solution to the problem of finding a code that has both exponentially decreasing error probability with increasing block length and polynomial-time decoding complexity. Concatenated codes became widely used in space communications in the 1970s. Background The field of channel coding is concerned with sending a stream of data at the highest possible rate over a given communications channel, and then decoding the original data reliably at the receiver, using encoding and decoding algorithms that are feasible to implement in a given technology. Shannon's channel coding theorem shows that over many common channels there exist channel coding schemes that are able to transmit data reliably at all rates R less than a certain threshold C, called the channel capacity of the given channel. In fact, the p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Majority Logic Decoding
In error detection and correction, majority logic decoding is a method to decode repetition codes, based on the assumption that the largest number of occurrences of a symbol was the transmitted symbol. Theory In a binary alphabet made of 0,1, if a (n,1) repetition code is used, then each input bit is mapped to the code word as a string of n-replicated input bits. Generally n=2t + 1, an odd number. The repetition codes can detect up to /2/math> transmission errors. Decoding errors occur when more than these transmission errors occur. Thus, assuming bit-transmission errors are independent, the probability of error for a repetition code is given by P_e = \sum_^ \epsilon^ (1-\epsilon)^{(n-k)}, where \epsilon is the error over the transmission channel. Algorithm Assumption: the code word is (n,1), where n=2t+1, an odd number. * Calculate the d_H Hamming weight of the repetition code. * if d_H \le t , decode code word to be all 0's * if d_H \ge t+1 , decode code word to be all 1's ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Code
In coding theory, a linear code is an error-correcting code for which any linear combination of Code word (communication), codewords is also a codeword. Linear codes are traditionally partitioned into block codes and convolutional codes, although turbo codes can be seen as a hybrid of these two types. Linear codes allow for more efficient encoding and decoding algorithms than other codes (cf. syndrome decoding). Linear codes are used in forward error correction and are applied in methods for transmitting symbols (e.g., bits) on a communications channel so that, if errors occur in the communication, some errors can be corrected or detected by the recipient of a message block. The codewords in a linear block code are blocks of symbols that are encoded using more symbols than the original value to be sent. A linear code of length ''n'' transmits blocks containing ''n'' symbols. For example, the [7,4,3] Hamming code is a linear binary code which represents 4-bit messages using 7-bit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |