Channel capacity on:
[Wikipedia]
[Google]
[Amazon]
Channel capacity, in
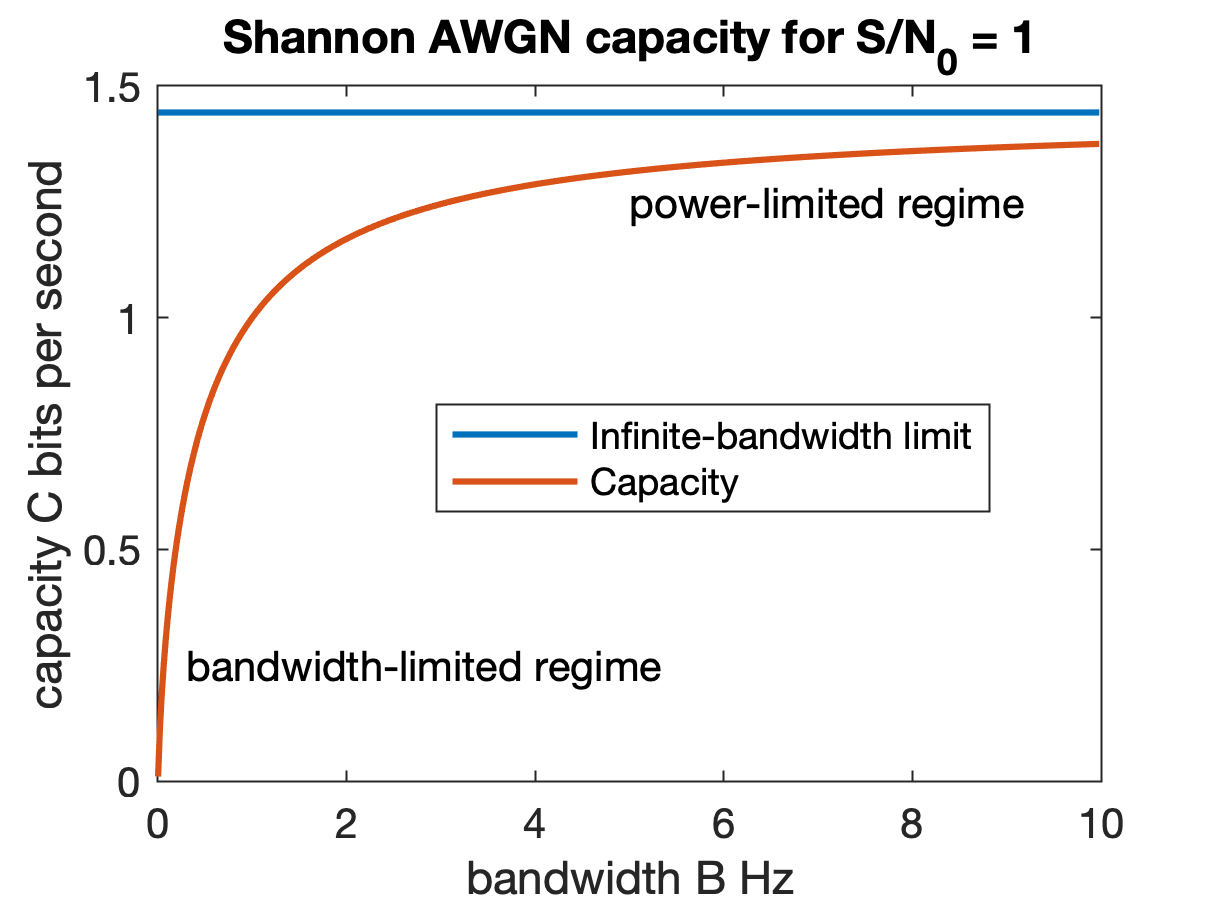 If the average received power is the total bandwidth is in Hertz, and the noise power spectral density is /Hz the AWGN channel capacity is
: its/s
where is the received signal-to-noise ratio (SNR). This result is known as the Shannon–Hartley theorem.
When the SNR is large (SNR ≫ 0 dB), the capacity is logarithmic in power and approximately linear in bandwidth. This is called the ''bandwidth-limited regime''.
When the SNR is small (SNR ≪ 0 dB), the capacity is linear in power but insensitive to bandwidth. This is called the ''power-limited regime''.
The bandwidth-limited regime and power-limited regime are illustrated in the figure.
If the average received power is the total bandwidth is in Hertz, and the noise power spectral density is /Hz the AWGN channel capacity is
: its/s
where is the received signal-to-noise ratio (SNR). This result is known as the Shannon–Hartley theorem.
When the SNR is large (SNR ≫ 0 dB), the capacity is logarithmic in power and approximately linear in bandwidth. This is called the ''bandwidth-limited regime''.
When the SNR is small (SNR ≪ 0 dB), the capacity is linear in power but insensitive to bandwidth. This is called the ''power-limited regime''.
The bandwidth-limited regime and power-limited regime are illustrated in the figure.
electrical engineering
Electrical engineering is an engineering discipline concerned with the study, design, and application of equipment, devices, and systems that use electricity, electronics, and electromagnetism. It emerged as an identifiable occupation in the l ...
, computer science
Computer science is the study of computation, information, and automation. Computer science spans Theoretical computer science, theoretical disciplines (such as algorithms, theory of computation, and information theory) to Applied science, ...
, and information theory
Information theory is the mathematical study of the quantification (science), quantification, Data storage, storage, and telecommunications, communication of information. The field was established and formalized by Claude Shannon in the 1940s, ...
, is the theoretical maximum rate at which information
Information is an Abstraction, abstract concept that refers to something which has the power Communication, to inform. At the most fundamental level, it pertains to the Interpretation (philosophy), interpretation (perhaps Interpretation (log ...
can be reliably transmitted over a communication channel
A communication channel refers either to a physical transmission medium such as a wire, or to a logical connection over a multiplexed medium such as a radio channel in telecommunications and computer networking. A channel is used for infor ...
.
Following the terms of the noisy-channel coding theorem
In information theory, the noisy-channel coding theorem (sometimes Shannon's theorem or Shannon's limit), establishes that for any given degree of noise contamination of a communication channel, it is possible (in theory) to communicate discrete ...
, the channel capacity of a given channel is the highest information rate (in units of information
Information is an Abstraction, abstract concept that refers to something which has the power Communication, to inform. At the most fundamental level, it pertains to the Interpretation (philosophy), interpretation (perhaps Interpretation (log ...
per unit time) that can be achieved with arbitrarily small error probability.
Information theory
Information theory is the mathematical study of the quantification (science), quantification, Data storage, storage, and telecommunications, communication of information. The field was established and formalized by Claude Shannon in the 1940s, ...
, developed by Claude E. Shannon in 1948, defines the notion of channel capacity and provides a mathematical model by which it may be computed. The key result states that the capacity of the channel, as defined above, is given by the maximum of the mutual information
In probability theory and information theory, the mutual information (MI) of two random variables is a measure of the mutual Statistical dependence, dependence between the two variables. More specifically, it quantifies the "Information conten ...
between the input and output of the channel, where the maximization is with respect to the input distribution.
The notion of channel capacity has been central to the development of modern wireline and wireless communication systems, with the advent of novel error correction coding mechanisms that have resulted in achieving performance very close to the limits promised by channel capacity.
Formal definition
The basic mathematical model for a communication system is the following: : where: * is the message to be transmitted; * is the channel input symbol ( is a sequence of symbols) taken in analphabet
An alphabet is a standard set of letter (alphabet), letters written to represent particular sounds in a spoken language. Specifically, letters largely correspond to phonemes as the smallest sound segments that can distinguish one word from a ...
;
* is the channel output symbol ( is a sequence of symbols) taken in an alphabet ;
* is the estimate of the transmitted message;
* is the encoding function for a block of length ;
* is the noisy channel, which is modeled by a conditional probability distribution
In probability theory and statistics, the conditional probability distribution is a probability distribution that describes the probability of an outcome given the occurrence of a particular event. Given two jointly distributed random variables X ...
; and,
* is the decoding function for a block of length .
Let and be modeled as random variables. Furthermore, let be the conditional probability distribution
In probability theory and statistics, the conditional probability distribution is a probability distribution that describes the probability of an outcome given the occurrence of a particular event. Given two jointly distributed random variables X ...
function of given , which is an inherent fixed property of the communication channel. Then the choice of the marginal distribution
In probability theory and statistics, the marginal distribution of a subset of a collection of random variables is the probability distribution of the variables contained in the subset. It gives the probabilities of various values of the variable ...
completely determines the joint distribution
A joint or articulation (or articular surface) is the connection made between bones, ossicles, or other hard structures in the body which link an animal's skeletal system into a functional whole.Saladin, Ken. Anatomy & Physiology. 7th ed. McGraw- ...
due to the identity
:
which, in turn, induces a mutual information
In probability theory and information theory, the mutual information (MI) of two random variables is a measure of the mutual Statistical dependence, dependence between the two variables. More specifically, it quantifies the "Information conten ...
. The channel capacity is defined as
:
where the supremum
In mathematics, the infimum (abbreviated inf; : infima) of a subset S of a partially ordered set P is the greatest element in P that is less than or equal to each element of S, if such an element exists. If the infimum of S exists, it is unique, ...
is taken over all possible choices of .
Additivity of channel capacity
Channel capacity is additive over independent channels. It means that using two independent channels in a combined manner provides the same theoretical capacity as using them independently. More formally, let and be two independent channels modelled as above; having an input alphabet and an output alphabet . Idem for . We define the product channel as This theorem states:Shannon capacity of a graph
If ''G'' is anundirected graph
In discrete mathematics, particularly in graph theory, a graph is a structure consisting of a set of objects where some pairs of the objects are in some sense "related". The objects are represented by abstractions called '' vertices'' (also call ...
, it can be used to define a communications channel in which the symbols are the graph vertices, and two codewords may be confused with each other if their symbols in each position are equal or adjacent. The computational complexity of finding the Shannon capacity of such a channel remains open, but it can be upper bounded by another important graph invariant, the Lovász number.
Noisy-channel coding theorem
Thenoisy-channel coding theorem
In information theory, the noisy-channel coding theorem (sometimes Shannon's theorem or Shannon's limit), establishes that for any given degree of noise contamination of a communication channel, it is possible (in theory) to communicate discrete ...
states that for any error probability ε > 0 and for any transmission rate ''R'' less than the channel capacity ''C'', there is an encoding and decoding scheme transmitting data at rate ''R'' whose error probability is less than ε, for a sufficiently large block length. Also, for any rate greater than the channel capacity, the probability of error at the receiver goes to 0.5 as the block length goes to infinity.
Example application
An application of the channel capacity concept to anadditive white Gaussian noise
Additive white Gaussian noise (AWGN) is a basic noise model used in information theory to mimic the effect of many random processes that occur in nature. The modifiers denote specific characteristics:
* ''Additive'' because it is added to any nois ...
(AWGN) channel with ''B'' Hz bandwidth and signal-to-noise ratio
Signal-to-noise ratio (SNR or S/N) is a measure used in science and engineering that compares the level of a desired signal to the level of background noise. SNR is defined as the ratio of signal power to noise power, often expressed in deci ...
''S/N'' is the Shannon–Hartley theorem
In information theory, the Shannon–Hartley theorem tells the maximum rate at which information can be transmitted over a communications channel of a specified bandwidth in the presence of noise. It is an application of the noisy-channel coding ...
:
:
''C'' is measured in bits per second
In telecommunications and computing, bit rate (bitrate or as a variable ''R'') is the number of bits that are conveyed or processed per unit of time.
The bit rate is expressed in the unit bit per second (symbol: bit/s), often in conjunction ...
if the logarithm
In mathematics, the logarithm of a number is the exponent by which another fixed value, the base, must be raised to produce that number. For example, the logarithm of to base is , because is to the rd power: . More generally, if , the ...
is taken in base 2, or nats per second if the natural logarithm
The natural logarithm of a number is its logarithm to the base of a logarithm, base of the e (mathematical constant), mathematical constant , which is an Irrational number, irrational and Transcendental number, transcendental number approxima ...
is used, assuming ''B'' is in hertz
The hertz (symbol: Hz) is the unit of frequency in the International System of Units (SI), often described as being equivalent to one event (or Cycle per second, cycle) per second. The hertz is an SI derived unit whose formal expression in ter ...
; the signal and noise powers ''S'' and ''N'' are expressed in a linear power unit (like watts or volts2). Since ''S/N'' figures are often cited in dB, a conversion may be needed. For example, a signal-to-noise ratio of 30 dB corresponds to a linear power ratio of .
Channel capacity estimation
To determine the channel capacity, it is necessary to find the capacity-achieving distribution and evaluate themutual information
In probability theory and information theory, the mutual information (MI) of two random variables is a measure of the mutual Statistical dependence, dependence between the two variables. More specifically, it quantifies the "Information conten ...
. Research has mostly focused on studying additive noise channels under certain power constraints and noise distributions, as analytical methods are not feasible in the majority of other scenarios. Hence, alternative approaches such as, investigation on the input support, relaxations and capacity bounds, have been proposed in the literature.
The capacity of a discrete memoryless channel can be computed using the Blahut-Arimoto algorithm.
Deep learning
Deep learning is a subset of machine learning that focuses on utilizing multilayered neural networks to perform tasks such as classification, regression, and representation learning. The field takes inspiration from biological neuroscience a ...
can be used to estimate the channel capacity. In fact, the channel capacity and the capacity-achieving distribution of any discrete-time continuous memoryless vector channel can be obtained using CORTICAL, a cooperative framework inspired by generative adversarial networks. CORTICAL consists of two cooperative networks: a generator with the objective of learning to sample from the capacity-achieving input distribution, and a discriminator with the objective to learn to distinguish between paired and unpaired channel input-output samples and estimates .
Channel capacity in wireless communications
This section focuses on the single-antenna, point-to-point scenario. For channel capacity in systems with multiple antennas, see the article onMIMO
In radio, multiple-input and multiple-output (MIMO) () is a method for multiplying the capacity of a radio link using multiple transmission and receiving antennas to exploit multipath propagation. MIMO has become an essential element of wirel ...
.
Bandlimited AWGN channel
 If the average received power is the total bandwidth is in Hertz, and the noise power spectral density is /Hz the AWGN channel capacity is
: its/s
where is the received signal-to-noise ratio (SNR). This result is known as the Shannon–Hartley theorem.
When the SNR is large (SNR ≫ 0 dB), the capacity is logarithmic in power and approximately linear in bandwidth. This is called the ''bandwidth-limited regime''.
When the SNR is small (SNR ≪ 0 dB), the capacity is linear in power but insensitive to bandwidth. This is called the ''power-limited regime''.
The bandwidth-limited regime and power-limited regime are illustrated in the figure.
If the average received power is the total bandwidth is in Hertz, and the noise power spectral density is /Hz the AWGN channel capacity is
: its/s
where is the received signal-to-noise ratio (SNR). This result is known as the Shannon–Hartley theorem.
When the SNR is large (SNR ≫ 0 dB), the capacity is logarithmic in power and approximately linear in bandwidth. This is called the ''bandwidth-limited regime''.
When the SNR is small (SNR ≪ 0 dB), the capacity is linear in power but insensitive to bandwidth. This is called the ''power-limited regime''.
The bandwidth-limited regime and power-limited regime are illustrated in the figure.
Frequency-selective AWGN channel
The capacity of the frequency-selective channel is given by so-called water filling power allocation, : where and is the gain of subchannel , with chosen to meet the power constraint.Slow-fading channel
In a slow-fading channel, where the coherence time is greater than the latency requirement, there is no definite capacity as the maximum rate of reliable communications supported by the channel, , depends on the random channel gain , which is unknown to the transmitter. If the transmitter encodes data at rate its/s/Hz there is a non-zero probability that the decoding error probability cannot be made arbitrarily small, :