|
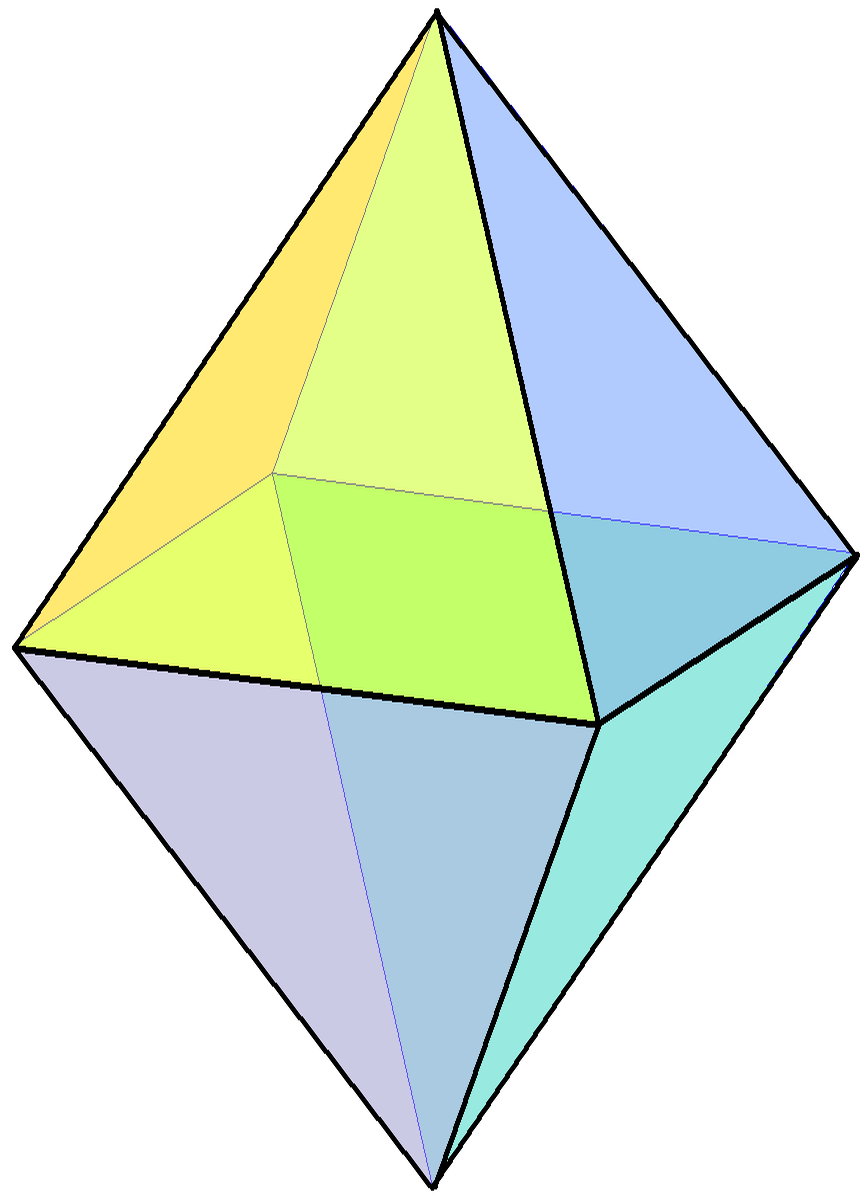
Octahedral
In geometry, an octahedron (: octahedra or octahedrons) is any polyhedron with eight faces. One special case is the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. Many types of irregular octahedra also exist, including both convex set, convex and non-convex shapes. Combinatorially equivalent to the regular octahedron The following polyhedra are combinatorially equivalent to the regular octahedron. They all have six vertices, eight triangular faces, and twelve edges that correspond one-for-one with the features of it: * Triangular antiprisms: Two faces are equilateral, lie on parallel planes, and have a common axis of symmetry. The other six triangles are isosceles. The regular octahedron is a special case in which the six lateral triangles are also equilateral. * Tetragonal bipyramids, in which at least one of the equatorial quadrilaterals lies on a plane. The regular octahedron is a special case in which all thr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regular Octahedron
In geometry, a regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. Regular octahedra occur in nature as crystal structures. An octahedron, more generally, can be any eight-sided polyhedron; many types of irregular octahedra also exist. A regular octahedron is convex, meaning that for any two points within it, the line segment connecting them lies entirely within it. It is one of the eight convex deltahedra because all of the faces are equilateral triangles. It is a composite polyhedron made by attaching two equilateral square pyramids. Its dual polyhedron is the cube, and they have the same three-dimensional symmetry groups, the octahedral symmetry \mathrm_\mathrm . A regular octahedron is a special case of an octahedron, any eight-sided polyhedron. It is the three-dimensional case of the more general concept of a cross-polytope. As a Platonic solid The regular octahedron is one of the Platonic solids, a s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Uniform Polyhedron
In geometry, a uniform polyhedron has regular polygons as Face (geometry), faces and is vertex-transitive—there is an isometry mapping any vertex onto any other. It follows that all vertices are congruence (geometry), congruent. Uniform polyhedra may be Regular polyhedron, regular (if also Isohedral figure, face- and Isotoxal figure, edge-transitive), Quasiregular polyhedron, quasi-regular (if also edge-transitive but not face-transitive), or Semiregular polyhedron, semi-regular (if neither edge- nor face-transitive). The faces and vertices don't need to be Convex polyhedron, convex, so many of the uniform polyhedra are also Star polyhedron, star polyhedra. There are two infinite classes of uniform polyhedra, together with 75 other polyhedra. They are 2 infinite classes of Prism (geometry), prisms and antiprisms, the convex polyhedrons as in 5 Platonic solids and 13 Archimedean solids—2 Quasiregular polyhedron, quasiregular and 11 Semiregular polyhedron, semiregular&m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Platonic Solid
In geometry, a Platonic solid is a Convex polytope, convex, regular polyhedron in three-dimensional space, three-dimensional Euclidean space. Being a regular polyhedron means that the face (geometry), faces are congruence (geometry), congruent (identical in shape and size) regular polygons (all angles congruent and all edge (geometry), edges congruent), and the same number of faces meet at each Vertex (geometry), vertex. There are only five such polyhedra: Geometers have studied the Platonic solids for thousands of years. They are named for the ancient Greek philosopher Plato, who hypothesized in one of his dialogues, the ''Timaeus (dialogue), Timaeus'', that the classical elements were made of these regular solids. History The Platonic solids have been known since antiquity. It has been suggested that certain carved stone balls created by the late Neolithic people of Scotland represent these shapes; however, these balls have rounded knobs rather than being polyhedral, the num ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangular Prisms
In geometry, a triangular prism or trigonal prism is a prism with 2 triangular bases. If the edges pair with each triangle's vertex and if they are perpendicular to the base, it is a ''right triangular prism''. A right triangular prism may be both semiregular and uniform. The triangular prism can be used in constructing another polyhedron. Examples are some of the Johnson solids, the truncated right triangular prism, and Schönhardt polyhedron. Properties A triangular prism has 6 vertices, 9 edges, and 5 faces. Every prism has 2 congruent faces known as its ''bases'', and the bases of a triangular prism are triangles. The triangle has 3 vertices, each of which pairs with another triangle's vertex, making up another 3 edges. These edges form 3 parallelograms as other faces. If the prism's edges are perpendicular to the base, the lateral faces are rectangles, and the prism is called a ''right triangular prism''. This prism may also be considered a special case of a wedge. If ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Octahedron
In geometry, an octahedron (: octahedra or octahedrons) is any polyhedron with eight faces. One special case is the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. Many types of irregular octahedra also exist, including both convex set, convex and non-convex shapes. Combinatorially equivalent to the regular octahedron The following polyhedra are combinatorially equivalent to the regular octahedron. They all have six vertices, eight triangular faces, and twelve edges that correspond one-for-one with the features of it: * Triangular antiprisms: Two faces are equilateral, lie on parallel planes, and have a common axis of symmetry. The other six triangles are isosceles. The regular octahedron is a special case in which the six lateral triangles are also equilateral. * Tetragonal bipyramids, in which at least one of the equatorial quadrilaterals lies on a plane. The regular octahedron is a special case in which all thr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangular Cupola
In geometry, the triangular cupola is the cupola with hexagon as its base and triangle as its top. If the edges are equal in length, the triangular cupola is the Johnson solid. It can be seen as half a cuboctahedron. The triangular cupola can be applied to construct many polyhedrons. Properties The triangular cupola has 4 triangles, 3 squares, and 1 hexagon as their faces; the hexagon is the base and one of the four triangles is the top. If all of the edges are equal in length, the triangles and the hexagon becomes regular. The dihedral angle between each triangle and the hexagon is approximately 70.5°, that between each square and the hexagon is 54.7°, and that between square and triangle is 125.3°. A convex polyhedron in which all of the faces are regular is a Johnson solid, and the triangular cupola is among them, enumerated as the third Johnson solid J_ . Given that a is the edge length of a triangular cupola. Its surface area A can be calculated by adding t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dual Polyhedron
In geometry, every polyhedron is associated with a second dual structure, where the vertices of one correspond to the faces of the other, and the edges between pairs of vertices of one correspond to the edges between pairs of faces of the other. Such dual figures remain combinatorial or abstract polyhedra, but not all can also be constructed as geometric polyhedra. Starting with any given polyhedron, the dual of its dual is the original polyhedron. Duality preserves the symmetries of a polyhedron. Therefore, for many classes of polyhedra defined by their symmetries, the duals belong to a corresponding symmetry class. For example, the regular polyhedrathe (convex) Platonic solids and (star) Kepler–Poinsot polyhedraform dual pairs, where the regular tetrahedron is self-dual. The dual of an isogonal polyhedron (one in which any two vertices are equivalent under symmetries of the polyhedron) is an isohedral polyhedron (one in which any two faces are equivalent .., and vice ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Augmented Triangular Prism
In geometry, the augmented triangular prism is a polyhedron constructed by attaching an equilateral square pyramid onto the square face of a triangular prism. As a result, it is an example of Johnson solid. It can be visualized as the chemical compound, known as capped trigonal prismatic molecular geometry. Construction The augmented triangular prism can be constructed from a triangular prism by attaching an equilateral square pyramid to one of its square faces, a process known as augmentation. This square pyramid covers the square face of the prism, so the resulting polyhedron has 6 equilateral triangles and 2 squares as its faces. A convex polyhedron in which all faces are regular is Johnson solid, and the augmented triangular prism is among them, enumerated as 49th Johnson solid J_ . Properties An augmented triangular prism with edge length a has a surface area, calculated by adding six equilateral triangles and two squares' area: \fraca^2 \approx 4.598a^2. Its v ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square Pyramid
In geometry, a square pyramid is a Pyramid (geometry), pyramid with a square base and four triangles, having a total of five faces. If the Apex (geometry), apex of the pyramid is directly above the center of the square, it is a ''right square pyramid'' with four isosceles triangles; otherwise, it is an ''oblique square pyramid''. When all of the pyramid's edges are equal in length, its triangles are all equilateral triangle, equilateral. It is called an ''equilateral square pyramid'', an example of a Johnson solid. Square pyramids have appeared throughout the history of architecture, with examples being Egyptian pyramids and many other similar buildings. They also occur in chemistry in Square pyramidal molecular geometry, square pyramidal molecular structures. Square pyramids are often used in the construction of other polyhedra. Many mathematicians in ancient times discovered the formula for the volume of a square pyramid with different approaches. Special cases Right squar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isosceles Triangle
In geometry, an isosceles triangle () is a triangle that has two Edge (geometry), sides of equal length and two angles of equal measure. Sometimes it is specified as having ''exactly'' two sides of equal length, and sometimes as having ''at least'' two sides of equal length, the latter version thus including the equilateral triangle as a special case. Examples of isosceles triangles include the isosceles right triangle, the Golden triangle (mathematics), golden triangle, and the faces of bipyramids and certain Catalan solids. The mathematical study of isosceles triangles dates back to ancient Egyptian mathematics and Babylonian mathematics. Isosceles triangles have been used as decoration from even earlier times, and appear frequently in architecture and design, for instance in the pediments and gables of buildings. The two equal sides are called the ''legs'' and the third side is called the base (geometry), ''base'' of the triangle. The other dimensions of the triangle, such ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pyramid (geometry)
In geometry, a pyramid is a polyhedron formed by connecting a polygonal base and a point, called the apex (geometry), apex. Each base edge (geometry), edge and apex form a triangle, called a lateral face. A pyramid is a cone, conic solid with a polygonal base. Many types of pyramids can be found by determining the shape of bases, either by based on a regular polygon (regular pyramids) or by cutting off the apex (truncated pyramid). It can be generalized into higher dimensions, known as hyperpyramid. All pyramids are Self-dual polyhedron, self-dual. Etymology The word "pyramid" derives from the ancient Greek term "πυραμίς" (pyramis), which referred to a pyramid-shaped structure and a type of wheat cake. The term is rooted in the Greek "πυρ" (pyr, 'fire') and "άμις" (amis, 'vessel'), highlighting the shape's pointed, flame-like appearance. In Byzantine Greek, the term evolved to "πυραμίδα" (pyramída), continuing to denote pyramid structures. The Greek term " ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heptagon
In geometry, a heptagon or septagon is a seven-sided polygon or 7-gon. The heptagon is sometimes referred to as the septagon, using ''Wikt:septa-, septa-'' (an elision of ''Wikt:septua-, septua-''), a Latin-derived numerical prefix, rather than ''Wikt:hepta-, hepta-'', a Greek language, Greek-derived numerical prefix (both are cognate), together with the suffix ''-gon'' for , meaning angle. Regular heptagon A regular polygon, regular heptagon, in which all sides and all angles are equal, has internal angles of 5π/7 radians (128 degree (angle), degrees). Its Schläfli symbol is . Area The area (''A'') of a regular heptagon of side length ''a'' is given by: :A = \fraca^2 \cot \frac \simeq 3.634 a^2. This can be seen by subdividing the unit-sided heptagon into seven triangular "pie slices" with Vertex (geometry), vertices at the center and at the heptagon's vertices, and then halving each triangle using the apothem as the common side. The apothem is half the cotangent of \pi/7 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |