square pyramid on:
[Wikipedia]
[Google]
[Amazon]
In
 If all triangular edges are of equal length, the four triangles are
If all triangular edges are of equal length, the four triangles are
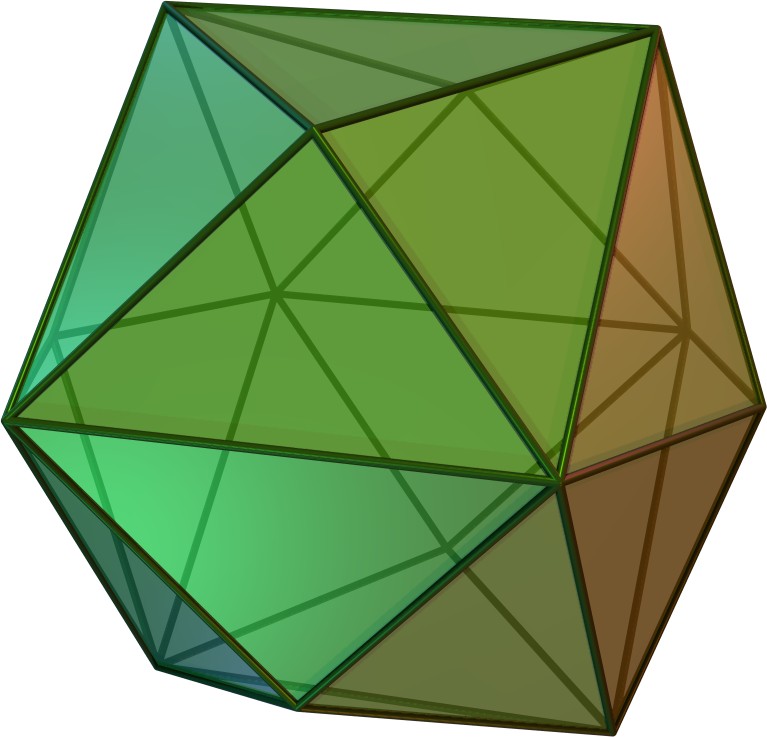 The base of a square pyramid can be attached to a square face of another polyhedron to construct new polyhedra, an example of augmentation. For example, a tetrakis hexahedron can be constructed by attaching the base of an equilateral square pyramid onto each face of a cube. Attaching prisms or antiprisms to pyramids is known as elongation or gyroelongation, respectively. Some of the other Johnson solids can be constructed by either augmenting square pyramids or augmenting other shapes with square pyramids: elongated square pyramid , gyroelongated square pyramid , elongated square bipyramid , gyroelongated square bipyramid , augmented triangular prism , biaugmented triangular prism , triaugmented triangular prism ,
The base of a square pyramid can be attached to a square face of another polyhedron to construct new polyhedra, an example of augmentation. For example, a tetrakis hexahedron can be constructed by attaching the base of an equilateral square pyramid onto each face of a cube. Attaching prisms or antiprisms to pyramids is known as elongation or gyroelongation, respectively. Some of the other Johnson solids can be constructed by either augmenting square pyramids or augmenting other shapes with square pyramids: elongated square pyramid , gyroelongated square pyramid , elongated square bipyramid , gyroelongated square bipyramid , augmented triangular prism , biaugmented triangular prism , triaugmented triangular prism ,
84–89
See Table 12.3, where denotes the prism and denotes the antiprism.
Square Pyramid
– Interactive Polyhedron Model
georgehart.com: The Encyclopedia of Polyhedra ( VRMLbr>model
) {{Johnson solids Elementary polyhedron Johnson solids Prismatoid polyhedra Pyramids (geometry) Self-dual polyhedra
geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician w ...
, a square pyramid is a pyramid
A pyramid () is a structure whose visible surfaces are triangular in broad outline and converge toward the top, making the appearance roughly a pyramid in the geometric sense. The base of a pyramid can be of any polygon shape, such as trian ...
with a square base and four triangles, having a total of five faces. If the apex
The apex is the highest point of something. The word may also refer to:
Arts and media Fictional entities
* Apex (comics)
A-Bomb
Abomination
Absorbing Man
Abraxas
Abyss
Abyss is the name of two characters appearing in Ameri ...
of the pyramid is directly above the center of the square, it is a ''right square pyramid'' with four isosceles triangle
In geometry, an isosceles triangle () is a triangle that has two Edge (geometry), sides of equal length and two angles of equal measure. Sometimes it is specified as having ''exactly'' two sides of equal length, and sometimes as having ''at le ...
s; otherwise, it is an ''oblique square pyramid''. When all of the pyramid's edges are equal in length, its triangles are all equilateral
An equilateral triangle is a triangle in which all three sides have the same length, and all three angles are equal. Because of these properties, the equilateral triangle is a regular polygon, occasionally known as the regular triangle. It is the ...
. It is called an ''equilateral square pyramid'', an example of a Johnson solid
In geometry, a Johnson solid, sometimes also known as a Johnson–Zalgaller solid, is a convex polyhedron whose faces are regular polygons. They are sometimes defined to exclude the uniform polyhedrons. There are ninety-two Solid geometry, s ...
.
Square pyramids have appeared throughout the history of architecture, with examples being Egyptian pyramids and many other similar buildings. They also occur in chemistry in square pyramidal molecular structures. Square pyramids are often used in the construction of other polyhedra
In geometry, a polyhedron (: polyhedra or polyhedrons; ) is a three-dimensional figure with flat polygonal faces, straight edges and sharp corners or vertices. The term "polyhedron" may refer either to a solid figure or to its boundary su ...
. Many mathematicians in ancient times discovered the formula for the volume of a square pyramid with different approaches.
Special cases
Right square pyramid
A square pyramid has five vertices, eight edges, and five faces. One face, called the ''base'' of the pyramid, is asquare
In geometry, a square is a regular polygon, regular quadrilateral. It has four straight sides of equal length and four equal angles. Squares are special cases of rectangles, which have four equal angles, and of rhombuses, which have four equal si ...
; the four other faces are triangle
A triangle is a polygon with three corners and three sides, one of the basic shapes in geometry. The corners, also called ''vertices'', are zero-dimensional points while the sides connecting them, also called ''edges'', are one-dimension ...
s. Four of the edges make up the square by connecting its four vertices. The other four edges are known as the lateral edges of the pyramid; they meet at the fifth vertex, called the apex
The apex is the highest point of something. The word may also refer to:
Arts and media Fictional entities
* Apex (comics)
A-Bomb
Abomination
Absorbing Man
Abraxas
Abyss
Abyss is the name of two characters appearing in Ameri ...
. If the pyramid's apex lies on a line erected perpendicularly from the center of the square, it is called a ''right square pyramid'', and the four triangular faces are isosceles triangle
In geometry, an isosceles triangle () is a triangle that has two Edge (geometry), sides of equal length and two angles of equal measure. Sometimes it is specified as having ''exactly'' two sides of equal length, and sometimes as having ''at le ...
s. Otherwise, the pyramid has two or more non-isosceles triangular faces and is called an ''oblique square pyramid''.
The ''slant height'' of a right square pyramid is defined as the height of one of its isosceles triangles. It can be obtained via the Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite t ...
:
where is the length of the triangle's base, also one of the square's edges, and is the length of the triangle's legs, which are lateral edges of the pyramid. The height of a right square pyramid can be similarly obtained, with a substitution of the slant height formula giving:
A polyhedron
In geometry, a polyhedron (: polyhedra or polyhedrons; ) is a three-dimensional figure with flat polygonal Face (geometry), faces, straight Edge (geometry), edges and sharp corners or Vertex (geometry), vertices. The term "polyhedron" may refer ...
's surface area
The surface area (symbol ''A'') of a solid object is a measure of the total area that the surface of the object occupies. The mathematical definition of surface area in the presence of curved surfaces is considerably more involved than the d ...
is the sum of the areas of its faces. The surface area of a right square pyramid can be expressed as , where and are the areas of one of its triangles and its base, respectively. The area of a triangle is half of the product of its base and side, with the area of a square being the length of the side squared. This gives the expression:
In general, the volume of a pyramid is equal to one-third of the area of its base multiplied by its height. Expressed in a formula for a square pyramid, this is:
Many mathematicians have discovered the formula for calculating the volume of a square pyramid in ancient times. In the Moscow Mathematical Papyrus
The Moscow Mathematical Papyrus, also named the Golenishchev Mathematical Papyrus after its first non-Egyptian owner, Egyptologist Vladimir Golenishchev, is an ancient Egyptian mathematical papyrus containing several problems in arithmetic, ge ...
, Egyptian mathematicians demonstrated knowledge of the formula for calculating the volume of a truncated square pyramid, suggesting that they were also acquainted with the volume of a square pyramid, but it is unknown how the formula was derived. Beyond the discovery of the volume of a square pyramid, the problem of finding the slope and height of a square pyramid can be found in the Rhind Mathematical Papyrus
The Rhind Mathematical Papyrus (RMP; also designated as papyrus British Museum 10057, pBM 10058, and Brooklyn Museum 37.1784Ea-b) is one of the best known examples of ancient Egyptian mathematics.
It is one of two well-known mathematical papyri ...
. The Babylonian mathematicians also considered the volume of a frustum, but gave an incorrect formula for it. One Chinese mathematician Liu Hui
Liu Hui () was a Chinese mathematician who published a commentary in 263 CE on ''Jiu Zhang Suan Shu ( The Nine Chapters on the Mathematical Art).'' He was a descendant of the Marquis of Zixiang of the Eastern Han dynasty and lived in the state ...
also discovered the volume by the method of dissecting a rectangular solid into pieces.
Equilateral square pyramid
equilateral
An equilateral triangle is a triangle in which all three sides have the same length, and all three angles are equal. Because of these properties, the equilateral triangle is a regular polygon, occasionally known as the regular triangle. It is the ...
, and the pyramid's faces are all regular polygon
In Euclidean geometry, a regular polygon is a polygon that is Equiangular polygon, direct equiangular (all angles are equal in measure) and Equilateral polygon, equilateral (all sides have the same length). Regular polygons may be either ''convex ...
s, it is an ''equilateral square pyramid.'' The dihedral angles between adjacent triangular faces are , and that between the base and each triangular face being half of that, . A convex
Convex or convexity may refer to:
Science and technology
* Convex lens, in optics
Mathematics
* Convex set, containing the whole line segment that joins points
** Convex polygon, a polygon which encloses a convex set of points
** Convex polytop ...
polyhedron in which all of the faces are regular polygons
In Euclidean geometry, a regular polygon is a polygon that is Equiangular polygon, direct equiangular (all angles are equal in measure) and Equilateral polygon, equilateral (all sides have the same length). Regular polygons may be either ''convex ...
is called a Johnson solid
In geometry, a Johnson solid, sometimes also known as a Johnson–Zalgaller solid, is a convex polyhedron whose faces are regular polygons. They are sometimes defined to exclude the uniform polyhedrons. There are ninety-two Solid geometry, s ...
. The equilateral square pyramid is among them, enumerated as the first Johnson solid .
Because its edges are all equal in length (that is, ), its slant, height, surface area, and volume can be derived by substituting the formulas of a right square pyramid:
Like other right pyramids with a regular polygon as a base, a right square pyramid has pyramidal symmetry. For the square pyramid, this is the symmetry of cyclic group
In abstract algebra, a cyclic group or monogenous group is a Group (mathematics), group, denoted C_n (also frequently \Z_n or Z_n, not to be confused with the commutative ring of P-adic number, -adic numbers), that is Generating set of a group, ge ...
: the pyramid is left invariant by rotations of one-, two-, and three-quarters of a full turn around its axis of symmetry
An axis (: axes) may refer to:
Mathematics
*A specific line (often a directed line) that plays an important role in some contexts. In particular:
** Coordinate axis of a coordinate system
*** ''x''-axis, ''y''-axis, ''z''-axis, common names f ...
, the line connecting the apex to the center of the base; and is also mirror symmetric relative to any perpendicular plane passing through a bisector of the base. It can be represented as the wheel graph , meaning its skeleton
A skeleton is the structural frame that supports the body of most animals. There are several types of skeletons, including the exoskeleton, which is a rigid outer shell that holds up an organism's shape; the endoskeleton, a rigid internal fra ...
can be interpreted as a square in which its four vertices connects a vertex in the center called the universal vertex
In graph theory, a universal vertex is a Vertex (graph theory), vertex of an undirected graph that is adjacent to all other vertices of the graph. It may also be called a dominating vertex, as it forms a one-element dominating set in the graph. A ...
. It is self-dual, meaning its dual polyhedron
In geometry, every polyhedron is associated with a second dual structure, where the vertices of one correspond to the faces of the other, and the edges between pairs of vertices of one correspond to the edges between pairs of faces of the other ...
is the square pyramid itself.
An equilateral square pyramid is an elementary polyhedron. This means it cannot be separated by a plane to create two small convex polyhedrons with regular faces.
Applications
In architecture, the pyramids built in ancient Egypt are examples of buildings shaped like square pyramids. Pyramidologists have put forward various suggestions for the design of theGreat Pyramid of Giza
The Great Pyramid of Giza is the largest Egyptian pyramid. It served as the tomb of pharaoh Khufu, who ruled during the Fourth Dynasty of Egypt, Fourth Dynasty of the Old Kingdom of Egypt, Old Kingdom. Built , over a period of about 26 years ...
, including a theory based on the Kepler triangle and the golden ratio
In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their summation, sum to the larger of the two quantities. Expressed algebraically, for quantities and with , is in a golden ratio to if
\fr ...
. However, modern scholars favor descriptions using integer ratios, as being more consistent with the knowledge of Egyptian mathematics and proportion. The Mesoamerican pyramids
Mesoamerican pyramids form a prominent part of ancient Mesoamerican architecture. Although similar in some ways to Egyptian pyramids, these New World structures have flat tops (many with temples on the top) and stairs ascending their faces, more ...
are also ancient pyramidal buildings similar to the Egyptian; they differ in having flat tops and stairs ascending their faces. Modern buildings whose designs imitate the Egyptian pyramids include the Louvre Pyramid
The Louvre Pyramid () is a large glass-and-metal entrance way and skylight designed by the Chinese-American architect I. M. Pei. The pyramid is in the main courtyard (Cour Napoléon) of the Louvre Palace in Paris, surrounded by three smaller pyr ...
and the casino hotel Luxor Las Vegas.
In stereochemistry
Stereochemistry, a subdiscipline of chemistry, studies the spatial arrangement of atoms that form the structure of molecules and their manipulation. The study of stereochemistry focuses on the relationships between stereoisomers, which are defined ...
, an atom cluster
Nanoclusters are atomically precise, crystalline materials most often existing on the 0-2 nanometer scale. They are often considered kinetically stable intermediates that form during the synthesis of comparatively larger materials such as semic ...
can have a square pyramidal geometry. A square pyramidal molecule has a main-group element
In chemistry and atomic physics, the main group is the group (periodic table), group of chemical element, elements (sometimes called the representative elements) whose lightest members are represented by helium, lithium, beryllium, boron, carbon ...
with one active lone pair
In chemistry, a lone pair refers to a pair of valence electrons that are not shared with another atom in a covalent bondIUPAC ''Gold Book'' definition''lone (electron) pair''/ref> and is sometimes called an unshared pair or non-bonding pair. Lone ...
, which can be described by a model that predicts the geometry of molecules known as VSEPR theory
Valence shell electron pair repulsion (VSEPR) theory ( , ) is a conceptual model, model used in chemistry to predict the geometry of individual molecules from the number of electron pairs surrounding their central atoms. It is also named the Gill ...
. Examples of molecules with this structure include chlorine pentafluoride, bromine pentafluoride, and iodine pentafluoride.
 The base of a square pyramid can be attached to a square face of another polyhedron to construct new polyhedra, an example of augmentation. For example, a tetrakis hexahedron can be constructed by attaching the base of an equilateral square pyramid onto each face of a cube. Attaching prisms or antiprisms to pyramids is known as elongation or gyroelongation, respectively. Some of the other Johnson solids can be constructed by either augmenting square pyramids or augmenting other shapes with square pyramids: elongated square pyramid , gyroelongated square pyramid , elongated square bipyramid , gyroelongated square bipyramid , augmented triangular prism , biaugmented triangular prism , triaugmented triangular prism ,
The base of a square pyramid can be attached to a square face of another polyhedron to construct new polyhedra, an example of augmentation. For example, a tetrakis hexahedron can be constructed by attaching the base of an equilateral square pyramid onto each face of a cube. Attaching prisms or antiprisms to pyramids is known as elongation or gyroelongation, respectively. Some of the other Johnson solids can be constructed by either augmenting square pyramids or augmenting other shapes with square pyramids: elongated square pyramid , gyroelongated square pyramid , elongated square bipyramid , gyroelongated square bipyramid , augmented triangular prism , biaugmented triangular prism , triaugmented triangular prism , augmented pentagonal prism
Augment or augmentation may refer to:
Language
*Augment (Indo-European), a syllable added to the beginning of the word in certain Indo-European languages
* Augment (Bantu languages), a morpheme that is prefixed to the noun class prefix of nouns ...
, biaugmented pentagonal prism , augmented hexagonal prism , parabiaugmented hexagonal prism , metabiaugmented hexagonal prism , triaugmented hexagonal prism , and augmented sphenocorona ., pp84–89
See Table 12.3, where denotes the prism and denotes the antiprism.
See also
* Square pyramidal number, a natural number that counts the number of stacked spheres in a square pyramid.References
Notes
Works cited
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *External links
*Square Pyramid
– Interactive Polyhedron Model
georgehart.com: The Encyclopedia of Polyhedra ( VRMLbr>model
) {{Johnson solids Elementary polyhedron Johnson solids Prismatoid polyhedra Pyramids (geometry) Self-dual polyhedra