|
Spinor Bundle
In differential geometry, given a spin structure on an n-dimensional orientable Riemannian manifold (M, g),\, one defines the spinor bundle to be the complex vector bundle \pi_\colon\to M\, associated to the corresponding principal bundle \pi_\colon\to M\, of spin frames over M and the spin representation of its structure group (n)\, on the space of spinors \Delta_n. A section of the spinor bundle \, is called a spinor field. Formal definition Let (,F_) be a spin structure on a Riemannian manifold (M, g),\,that is, an equivariant lift of the oriented orthonormal frame bundle \mathrm F_(M)\to M with respect to the double covering \rho\colon (n)\to (n) of the special orthogonal group by the spin group. The spinor bundle \, is defined to be the complex vector bundle =\times_\Delta_n\, associated to the spin structure via the spin representation \kappa\colon (n)\to (\Delta_n),\, where ()\, denotes the group of unitary operators acting on a Hilbert space .\, The spin repr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differential Geometry
Differential geometry is a Mathematics, mathematical discipline that studies the geometry of smooth shapes and smooth spaces, otherwise known as smooth manifolds. It uses the techniques of Calculus, single variable calculus, vector calculus, linear algebra and multilinear algebra. The field has its origins in the study of spherical geometry as far back as classical antiquity, antiquity. It also relates to astronomy, the geodesy of the Earth, and later the study of hyperbolic geometry by Nikolai Lobachevsky, Lobachevsky. The simplest examples of smooth spaces are the Differential geometry of curves, plane and space curves and Differential geometry of surfaces, surfaces in the three-dimensional Euclidean space, and the study of these shapes formed the basis for development of modern differential geometry during the 18th and 19th centuries. Since the late 19th century, differential geometry has grown into a field concerned more generally with geometric structures on differentiable ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unitary Operator
In functional analysis, a unitary operator is a surjective bounded operator on a Hilbert space that preserves the inner product. Non-trivial examples include rotations, reflections, and the Fourier operator. Unitary operators generalize unitary matrices. Unitary operators are usually taken as operating ''on'' a Hilbert space, but the same notion serves to define the concept of isomorphism ''between'' Hilbert spaces. Definition Definition 1. A ''unitary operator'' is a bounded linear operator on a Hilbert space that satisfies , where is the adjoint of , and is the identity operator. The weaker condition defines an ''isometry''. The other weaker condition, , defines a ''coisometry''. Thus a unitary operator is a bounded linear operator that is both an isometry and a coisometry, or, equivalently, a surjective isometry. An equivalent definition is the following: Definition 2. A ''unitary operator'' is a bounded linear operator on a Hilbert space for which the followi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebraic Topology
Algebraic topology is a branch of mathematics that uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariant (mathematics), invariants that classification theorem, classify topological spaces up to homeomorphism, though usually most classify up to Homotopy#Homotopy equivalence and null-homotopy, homotopy equivalence. Although algebraic topology primarily uses algebra to study topological problems, using topology to solve algebraic problems is sometimes also possible. Algebraic topology, for example, allows for a convenient proof that any subgroup of a free group is again a free group. Main branches Below are some of the main areas studied in algebraic topology: Homotopy groups In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space. Intuitively, homotopy groups record information ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Princeton University Press
Princeton University Press is an independent publisher with close connections to Princeton University. Its mission is to disseminate scholarship within academia and society at large. The press was founded by Whitney Darrow, with the financial support of Charles Scribner, as a printing press to serve the Princeton community in 1905. Its distinctive building was constructed in 1911 on William Street in Princeton. Its first book was a new 1912 edition of John Witherspoon's ''Lectures on Moral Philosophy.'' History Princeton University Press was founded in 1905 by a recent Princeton graduate, Whitney Darrow, with financial support from another Princetonian, Charles Scribner II. Darrow and Scribner purchased the equipment and assumed the operations of two already existing local publishers, that of the ''Princeton Alumni Weekly'' and the Princeton Press. The new press printed both local newspapers, university documents, '' The Daily Princetonian'', and later added book publishing ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
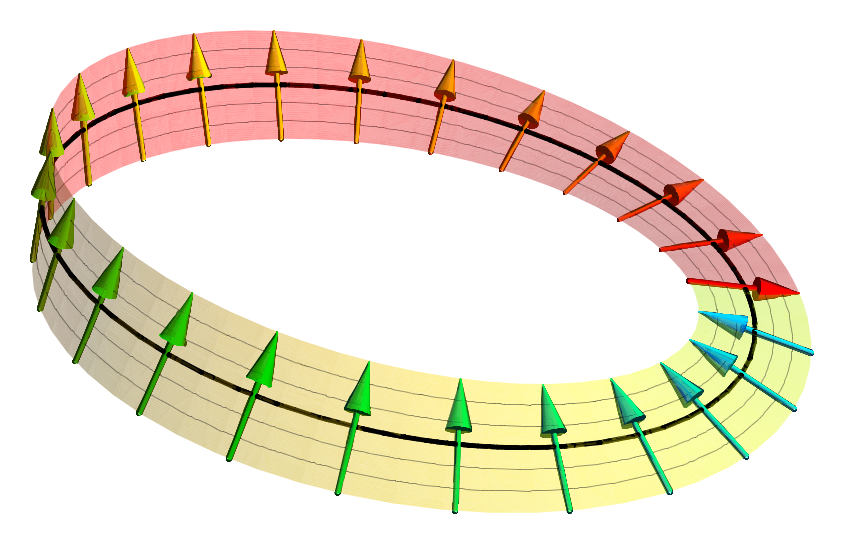
Spinor Representation
In geometry and physics, spinors (pronounced "spinner" IPA ) are elements of a complex vector space that can be associated with Euclidean space. A spinor transforms linearly when the Euclidean space is subjected to a slight (infinitesimal) rotation, but unlike geometric vectors and tensors, a spinor transforms to its negative when the space rotates through 360° (see picture). It takes a rotation of 720° for a spinor to go back to its original state. This property characterizes spinors: spinors can be viewed as the "square roots" of vectors (although this is inaccurate and may be misleading; they are better viewed as "square roots" of sections of vector bundles – in the case of the exterior algebra bundle of the cotangent bundle, they thus become "square roots" of differential forms). It is also possible to associate a substantially similar notion of spinor to Minkowski space, in which case the Lorentz transformations of special relativity play the role of rotations. Spinors ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spinor
In geometry and physics, spinors (pronounced "spinner" IPA ) are elements of a complex numbers, complex vector space that can be associated with Euclidean space. A spinor transforms linearly when the Euclidean space is subjected to a slight (infinitesimal transformation, infinitesimal) rotation, but unlike Euclidean vector, geometric vectors and tensors, a spinor transforms to its negative when the space rotates through 360° (see picture). It takes a rotation of 720° for a spinor to go back to its original state. This property characterizes spinors: spinors can be viewed as the "square roots" of vectors (although this is inaccurate and may be misleading; they are better viewed as "square roots" of Section (fiber bundle), sections of vector bundles – in the case of the exterior algebra bundle of the cotangent bundle, they thus become "square roots" of differential forms). It is also possible to associate a substantially similar notion of spinor to Minkowski space, in which cas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spin Geometry
In mathematics, spin geometry is the area of differential geometry and topology where objects like spin manifolds and Dirac operators, and the various associated index theorems have come to play a fundamental role both in mathematics and in mathematical physics. An important generalisation is the theory of symplectic Dirac operators in symplectic spin geometry and symplectic topology, which have become important fields of mathematical research. See also * Contact geometry * Symplectic topology * Spinor * Spinor bundle In differential geometry, given a spin structure on an n-dimensional orientable Riemannian manifold (M, g),\, one defines the spinor bundle to be the complex vector bundle \pi_\colon\to M\, associated to the corresponding principal bundle \pi_\co ... * Spin manifold Books * * Differential topology Differential geometry {{physics-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orthonormal Frame Bundle
In mathematics, a frame bundle is a principal fiber bundle F(E) associated with any vector bundle ''E''. The fiber of F(E) over a point ''x'' is the set of all ordered bases, or ''frames'', for ''E_x''. The general linear group acts naturally on F(E) via a change of basis, giving the frame bundle the structure of a principal ''\mathrm(k,\mathbb)''-bundle (where ''k'' is the rank of ''E''). The frame bundle of a smooth manifold is the one associated with its tangent bundle. For this reason it is sometimes called the tangent frame bundle. Definition and construction Let ''E \to X'' be a real vector bundle of rank ''k'' over a topological space ''X''. A frame at a point ''x \in X'' is an ordered basis for the vector space ''E_x''. Equivalently, a frame can be viewed as a linear isomorphism :p : \mathbf^k \to E_x. The set of all frames at ''x'', denoted ''F_x'', has a natural right action by the general linear group ''\mathrm(k,\mathbb)'' of invertible ''k \times k'' matrices: a gr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Clifford Module Bundle
In differential geometry, a Clifford module bundle, a bundle of Clifford modules or just Clifford module is a vector bundle whose fibers are Clifford modules, the representations of Clifford algebras. The canonical example is a spinor bundle. In fact, on a Spin manifold, every Clifford module is obtained by twisting the spinor bundle. The notion "Clifford module bundle" should not be confused with a Clifford bundle, which is a bundle of Clifford algebras. Spinor bundles Given an oriented Riemannian manifold ''M'' one can ask whether it is possible to construct a bundle of irreducible Clifford modules over ''Cℓ''(''T''*''M''). In fact, such a bundle can be constructed if and only if ''M'' is a spin manifold. Let ''M'' be an ''n''-dimensional spin manifold with spin structure ''F''Spin(''M'') → ''F''SO(''M'') on ''M''. Given any ''Cℓ''''n''R-module ''V'' one can construct the associated spinor bundle :S(M) = F_(M) \times_\sigma V\, where σ : Spin(''n'') → GL(''V'') i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Clifford Bundle
In mathematics, a Clifford bundle is an algebra bundle whose fibers have the structure of a Clifford algebra and whose local trivializations respect the algebra structure. There is a natural Clifford bundle associated to any (pseudo) Riemannian manifold ''M'' which is called the Clifford bundle of ''M''. This is commonly referred to as the Hopf fibration of S3, a topological construction pointed out by Heinz Hopf (1931). But Hopf’s procedure was explicitly based (with due reference) on an earlier geometrical construction of ‘ Clifford parallels’. General construction Let ''V'' be a ( real or complex) vector space together with a symmetric bilinear form . The Clifford algebra ''Cℓ''(''V'') is a natural ( unital associative) algebra generated by ''V'' subject only to the relation :v^2 = \langle v,v\rangle for all ''v'' in ''V''. One can construct ''Cℓ''(''V'') as a quotient of the tensor algebra of ''V'' by the ideal generated by the above relation. Like other tensor ope ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unitary Representation
In mathematics, a unitary representation of a group ''G'' is a linear representation π of ''G'' on a complex Hilbert space ''V'' such that π(''g'') is a unitary operator for every ''g'' ∈ ''G''. The general theory is well-developed in the case that ''G'' is a locally compact ( Hausdorff) topological group and the representations are strongly continuous. The theory has been widely applied in quantum mechanics since the 1920s, particularly influenced by Hermann Weyl's 1928 book '' Gruppentheorie und Quantenmechanik''. One of the pioneers in constructing a general theory of unitary representations, for any group ''G'' rather than just for particular groups useful in applications, was George Mackey. Context in harmonic analysis The theory of unitary representations of topological groups is closely connected with harmonic analysis. In the case of an abelian group ''G'', a fairly complete picture of the representation theory of ''G'' is given by Pontryagin duality. In genera ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hilbert Space
In mathematics, a Hilbert space is a real number, real or complex number, complex inner product space that is also a complete metric space with respect to the metric induced by the inner product. It generalizes the notion of Euclidean space. The inner product allows lengths and angles to be defined. Furthermore, Complete metric space, completeness means that there are enough limit (mathematics), limits in the space to allow the techniques of calculus to be used. A Hilbert space is a special case of a Banach space. Hilbert spaces were studied beginning in the first decade of the 20th century by David Hilbert, Erhard Schmidt, and Frigyes Riesz. They are indispensable tools in the theories of partial differential equations, mathematical formulation of quantum mechanics, quantum mechanics, Fourier analysis (which includes applications to signal processing and heat transfer), and ergodic theory (which forms the mathematical underpinning of thermodynamics). John von Neumann coined the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |