|
Skolem–Noether Theorem
In ring theory, a branch of mathematics, the Skolem–Noether theorem characterizes the automorphisms of simple rings. It is a fundamental result in the theory of central simple algebras. The theorem was first published by Thoralf Skolem in 1927 in his paper ''Zur Theorie der assoziativen Zahlensysteme'' (German: ''On the theory of associative number systems'') and later rediscovered by Emmy Noether. Statement In a general formulation, let ''A'' and ''B'' be simple unitary rings, and let ''k'' be the center of ''B''. The center ''k'' is a field since given ''x'' nonzero in ''k'', the simplicity of ''B'' implies that the nonzero two-sided ideal is the whole of ''B'', and hence that ''x'' is a unit. If the dimension of ''B'' over ''k'' is finite, i.e. if ''B'' is a central simple algebra of finite dimension, and ''A'' is also a ''k''-algebra, then given ''k''-algebra homomorphisms :''f'', ''g'' : ''A'' → ''B'', there exists a unit ''b'' in ''B'' such that for all ''a'' in '' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
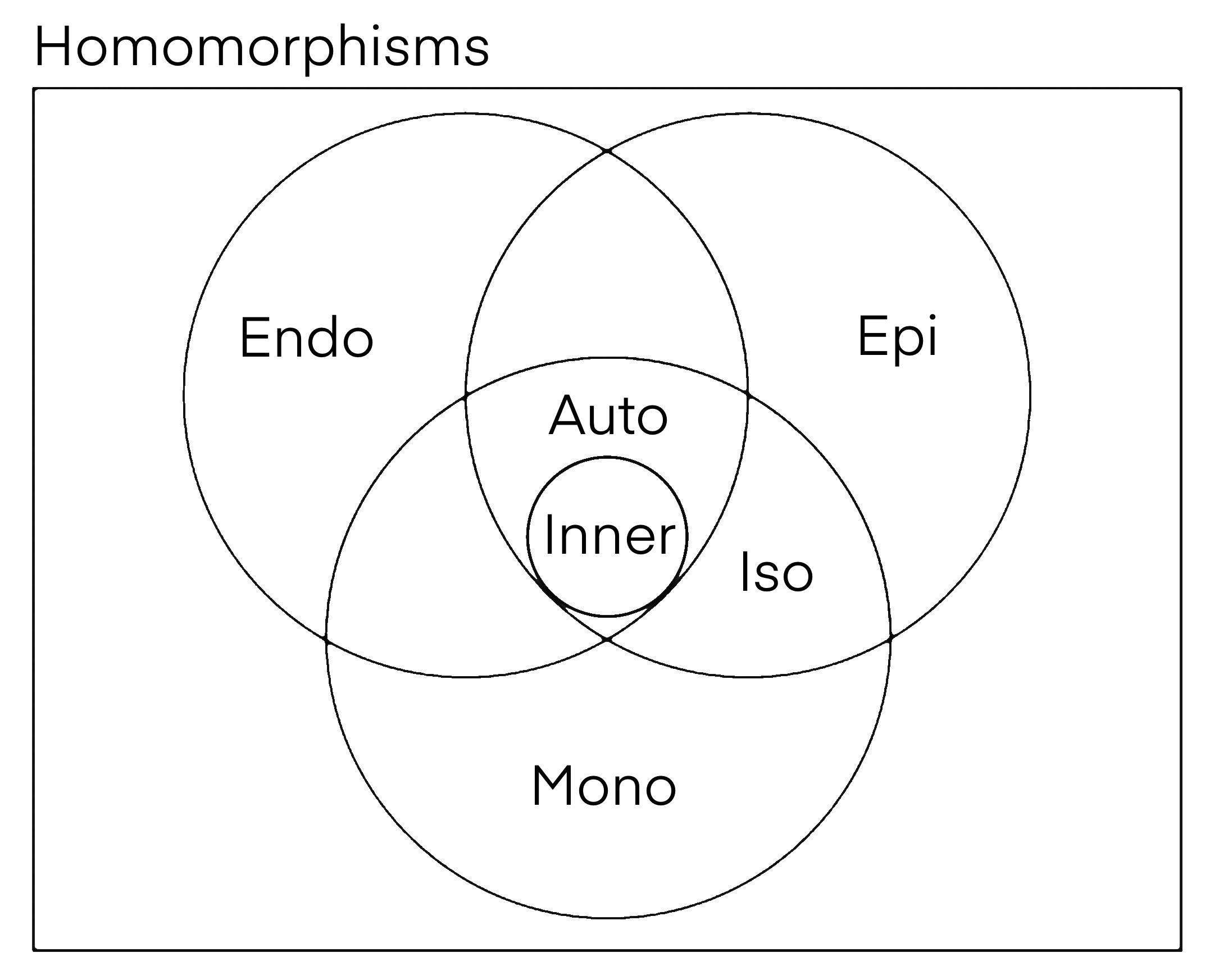
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism group. It is, loosely speaking, the symmetry group of the object. Definition In an algebraic structure such as a group, a ring, or vector space, an ''automorphism'' is simply a bijective homomorphism of an object into itself. (The definition of a homomorphism depends on the type of algebraic structure; see, for example, group homomorphism, ring homomorphism, and linear operator.) More generally, for an object in some category, an automorphism is a morphism of the object to itself that has an inverse morphism; that is, a morphism f: X\to X is an automorphism if there is a morphism g: X\to X such that g\circ f= f\circ g = \operatorname _X, where \operatorname _X is the identity ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Simple Ring
In abstract algebra, a branch of mathematics, a simple ring is a non-zero ring that has no two-sided ideal besides the zero ideal and itself. In particular, a commutative ring is a simple ring if and only if it is a field. The center of a simple ring is necessarily a field. It follows that a simple ring is an associative algebra over this field. It is then called a simple algebra over this field. Several references (e.g., or ) require in addition that a simple ring be left or right Artinian (or equivalently semi-simple). Under such terminology a non-zero ring with no non-trivial two-sided ideals is called quasi-simple. Rings which are simple as rings but are not a simple module over themselves do exist: a full matrix ring over a field does not have any nontrivial two-sided ideals (since any ideal of M_n(R) is of the form M_n(I) with I an ideal of R), but it has nontrivial left ideals (for example, the sets of matrices which have some fixed zero columns). An immediate e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Central Simple Algebra
In ring theory and related areas of mathematics a central simple algebra (CSA) over a field ''K'' is a finite-dimensional associative ''K''-algebra ''A'' that is simple, and for which the center is exactly ''K''. (Note that ''not'' every simple algebra is a central simple algebra over its center: for instance, if ''K'' is a field of characteristic 0, then the Weyl algebra K ,\partial_X/math> is a simple algebra with center ''K'', but is ''not'' a central simple algebra over ''K'' as it has infinite dimension as a ''K''-module.) For example, the complex numbers C form a CSA over themselves, but not over the real numbers R (the center of C is all of C, not just R). The quaternions H form a 4-dimensional CSA over R, and in fact represent the only non-trivial element of the Brauer group of the reals (see below). Given two central simple algebras ''A'' ~ ''M''(''n'',''S'') and ''B'' ~ ''M''(''m'',''T'') over the same field ''F'', ''A'' and ''B'' are called ''similar'' (or '' Brauer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thoralf Skolem
Thoralf Albert Skolem (; 23 May 1887 – 23 March 1963) was a Norwegian mathematician who worked in mathematical logic and set theory. Life Although Skolem's father was a primary school teacher, most of his extended family were farmers. Skolem attended secondary school in Kristiania (later renamed Oslo), passing the university entrance examinations in 1905. He then entered Det Kongelige Frederiks Universitet to study mathematics, also taking courses in physics, chemistry, zoology and botany. In 1909, he began working as an assistant to the physicist Kristian Birkeland, known for bombarding magnetized spheres with electrons and obtaining aurora-like effects; thus Skolem's first publications were physics papers written jointly with Birkeland. In 1913, Skolem passed the state examinations with distinction, and completed a dissertation titled ''Investigations on the Algebra of Logic''. He also traveled with Birkeland to the Sudan to observe the zodiacal light. He spent the wint ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
German Language
German (, ) is a West Germanic language in the Indo-European language family, mainly spoken in Western Europe, Western and Central Europe. It is the majority and Official language, official (or co-official) language in Germany, Austria, Switzerland, and Liechtenstein. It is also an official language of Luxembourg, German-speaking Community of Belgium, Belgium and the Italian autonomous province of South Tyrol, as well as a recognized national language in Namibia. There are also notable German-speaking communities in other parts of Europe, including: Poland (Upper Silesia), the Czech Republic (North Bohemia), Denmark (South Jutland County, North Schleswig), Slovakia (Krahule), Germans of Romania, Romania, Hungary (Sopron), and France (European Collectivity of Alsace, Alsace). Overseas, sizeable communities of German-speakers are found in the Americas. German is one of the global language system, major languages of the world, with nearly 80 million native speakers and over 130 mi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Emmy Noether
Amalie Emmy Noether (23 March 1882 – 14 April 1935) was a German mathematician who made many important contributions to abstract algebra. She also proved Noether's theorem, Noether's first and Noether's second theorem, second theorems, which are fundamental in mathematical physics. Noether was described by Pavel Alexandrov, Albert Einstein, Jean Dieudonné, Hermann Weyl and Norbert Wiener as the most important List of women in mathematics, woman in the history of mathematics. Transcribeonlineat the MacTutor History of Mathematics Archive. As one of the leading mathematicians of her time, she developed theories of ring (mathematics), rings, field (mathematics), fields, and algebras. In physics, Noether's theorem explains the connection between Symmetry (physics), symmetry and conservation laws. in . Noether was born to a Jewish family in the Franconian town of Erlangen; her father was the mathematician Max Noether. She originally planned to teach French and English after passin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Field (mathematics)
In mathematics, a field is a set (mathematics), set on which addition, subtraction, multiplication, and division (mathematics), division are defined and behave as the corresponding operations on rational number, rational and real numbers. A field is thus a fundamental algebraic structure which is widely used in algebra, number theory, and many other areas of mathematics. The best known fields are the field of rational numbers, the field of real numbers and the field of complex numbers. Many other fields, such as field of rational functions, fields of rational functions, algebraic function fields, algebraic number fields, and p-adic number, ''p''-adic fields are commonly used and studied in mathematics, particularly in number theory and algebraic geometry. Most cryptographic protocols rely on finite fields, i.e., fields with finitely many element (set), elements. The theory of fields proves that angle trisection and squaring the circle cannot be done with a compass and straighte ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unit (ring Theory)
In algebra, a unit or invertible element of a ring is an invertible element for the multiplication of the ring. That is, an element of a ring is a unit if there exists in such that vu = uv = 1, where is the multiplicative identity; the element is unique for this property and is called the multiplicative inverse of . The set of units of forms a group under multiplication, called the group of units or unit group of . Other notations for the unit group are , , and (from the German term ). Less commonly, the term ''unit'' is sometimes used to refer to the element of the ring, in expressions like ''ring with a unit'' or ''unit ring'', and also unit matrix. Because of this ambiguity, is more commonly called the "unity" or the "identity" of the ring, and the phrases "ring with unity" or a "ring with identity" may be used to emphasize that one is considering a ring instead of a rng. Examples The multiplicative identity and its additive inverse are always units. More ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dimension (vector Space)
In mathematics, the dimension of a vector space ''V'' is the cardinality (i.e., the number of vectors) of a Basis (linear algebra), basis of ''V'' over its base Field (mathematics), field. p. 44, §2.36 It is sometimes called Hamel dimension (after Georg Hamel) or algebraic dimension to distinguish it from other types of dimension. For every vector space there exists a basis, and all bases of a vector space have equal cardinality; as a result, the dimension of a vector space is uniquely defined. We say V is if the dimension of V is wiktionary:finite, finite, and if its dimension is infinity, infinite. The dimension of the vector space V over the field F can be written as \dim_F(V) or as [V : F], read "dimension of V over F". When F can be inferred from context, \dim(V) is typically written. Examples The vector space \R^3 has \left\ as a standard basis, and therefore \dim_(\R^3) = 3. More generally, \dim_(\R^n) = n, and even more generally, \dim_(F^n) = n for any Field (mathe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inner Automorphism
In abstract algebra, an inner automorphism is an automorphism of a group, ring, or algebra Algebra is a branch of mathematics that deals with abstract systems, known as algebraic structures, and the manipulation of expressions within those systems. It is a generalization of arithmetic that introduces variables and algebraic ope ... given by the conjugation action of a fixed element, called the ''conjugating element''. They can be realized via operations from within the group itself, hence the adjective "inner". These inner automorphisms form a subgroup of the automorphism group, and the Quotient_group, quotient of the automorphism group by this subgroup is defined as the outer automorphism group. Definition If is a group and is an element of (alternatively, if is a ring, and is a Unit (ring theory), unit), then the function :\begin \varphi_g\colon G&\to G \\ \varphi_g(x)&:= g^xg \end is called (right) conjugation by (see also conjugacy class). This func ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
James Milne (mathematician)
James S. Milne (born 10 October 1942 in Invercargill, New Zealand) is a New Zealand mathematician working in arithmetic geometry. Life Milne attended high school in Invercargill in New Zealand until 1959, and then studied at the University of Otago in Dunedin (B.A. 1964) and Harvard University (Masters 1966, Ph.D. 1967 under John Tate). From then to 1969 he was a lecturer at University College London. After that he was at the University of Michigan, as Assistant Professor (1969–1972), Associate Professor (1972–1977), Professor (1977–2000), and Professor Emeritus (since 2000). He has also been a visiting professor at King's College London, at the Institut des hautes études scientifiques in Paris (1975, 1978), at the Mathematical Sciences Research Institute in Berkeley, California (1986–87), and the Institute for Advanced Study in Princeton, New Jersey (1976–77, 1982, 1988). In his dissertation, entitled "The conjectures of Birch and Swinnerton-Dyer for constant ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |