|
Settling Velocity
Terminal velocity is the maximum speed attainable by an object as it falls through a fluid (air is the most common example). It is reached when the sum of the drag force (''Fd'') and the buoyancy is equal to the downward force of gravity (''FG'') acting on the object. Since the net force on the object is zero, the object has zero acceleration. For objects falling through air at normal pressure, the buoyant force is usually dismissed and not taken into account, as its effects are negligible. As the speed of an object increases, so does the drag force acting on it, which also depends on the substance it is passing through (for example air or water). At some speed, the drag or force of resistance will be equal to the gravitational pull on the object. At this point the object stops accelerating and continues falling at a constant speed called the terminal velocity (also called settling velocity). An object moving downward faster than the terminal velocity (for example because it ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Aviation, Space, And Environmental Medicine
''Aerospace Medicine and Human Performance'' (''AMHP'') is a peer-reviewed scientific journal in the field of aviation and aerospace medicine. It was founded as the ''Journal of Aviation Medicine'' in 1930 by Louis H. Bauer, M.D., and is published monthly by the Aerospace Medical Association.The ''Aviation, Space, and Environmental Medicine'' masthead. ''Aerospace Medicine and Human Performance'' is the most used and cited journal in its field, and is distributed to more than 80 nations. The journal was first published, under the title ''Journal of Aviation Medicine'' in 1930. In 1959 the title changed to ''Aerospace Medicine'', was renamed ''Aviation, Space, and Envir ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Types Of Equilibrium
This is a list presents the various articles at Wikipedia that use the term equilibrium (or an associated prefix or derivative) in their titles or leads. It is not necessarily complete; further examples may be found by using the Wikipedia search function, and this term. Biology * Equilibrioception, the sense of a balance present in human beings and animals * Equilibrium unfolding, the process of unfolding a protein or RNA molecule by gradually changing its environment * Genetic equilibrium, theoretical state in which a population is not evolving * Homeostasis, the ability of an open system, especially living organisms, to regulate its internal environment * Punctuated equilibrium, theory in evolutionary biology * Sedimentation equilibrium, analytical ultracentrifugation method for measuring protein molecular masses in solution * Equilibrium Theory ( Island biogeography), MacArthur-Wilson theory explaining biodiversity character of ecological islands * Osmotic equilibrium, ba ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Drag Equation
In fluid dynamics, the drag equation is a formula used to calculate the force of drag (physics), drag experienced by an object due to movement through a fully enclosing fluid. The equation is: F_\, =\, \tfrac12\, \rho\, u^2\, c_\, A where *F_ is the drag force, which is by definition the force component in the direction of the flow velocity, *\rho is the mass density of the fluid, *u is the flow velocity relative to the object, *A is the reference area, and *c_ is the drag coefficient – a dimensionless number, dimensionless physical coefficient, coefficient related to the object's geometry and taking into account both skin friction and form drag. If the fluid is a liquid, c_ depends on the Reynolds number; if the fluid is a gas, c_ depends on both the Reynolds number and the Mach number. The equation is attributed to Lord Rayleigh, who originally used ''L''2 in place of ''A'' (with ''L'' being some linear dimension). The reference area ''A'' is typically defined as the area of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Barometric Formula
The barometric formula is a formula used to model how the air pressure (or air density) changes with altitude. Pressure equations There are two equations for computing pressure as a function of height. The first equation is applicable to the atmospheric layers in which the temperature is assumed to vary with altitude at a non null lapse rate of L_b: P = P_ \left 1 - \frac (h - h_)\right The second equation is applicable to the atmospheric layers in which the temperature is assumed not to vary with altitude ( lapse rate is null): P = P_b \exp \left frac\right/math> where: *P_b = reference pressure *T_ = reference temperature ( K) *L_ = temperature lapse rate (K/m) in ISA *h = geopotential height at which pressure is calculated (m) *h_b = geopotential height of reference level ''b'' (meters; e.g., ''hb'' = 11 000 m) *R^* = universal gas constant: 8.3144598 J/(mol·K) *g_0 = gravitational acceleration: 9.80665 m/s2 *M = molar mass of Earth's air: 0.0289644&nb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Surface Area
The surface area (symbol ''A'') of a solid object is a measure of the total area that the surface of the object occupies. The mathematical definition of surface area in the presence of curved surfaces is considerably more involved than the definition of arc length of one-dimensional curves, or of the surface area for polyhedra (i.e., objects with flat polygonal faces), for which the surface area is the sum of the areas of its faces. Smooth surfaces, such as a sphere, are assigned surface area using their representation as parametric surfaces. This definition of surface area is based on methods of infinitesimal calculus and involves partial derivatives and double integration. A general definition of surface area was sought by Henri Lebesgue and Hermann Minkowski at the turn of the twentieth century. Their work led to the development of geometric measure theory, which studies various notions of surface area for irregular objects of any dimension. An important example is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Volume
Volume is a measure of regions in three-dimensional space. It is often quantified numerically using SI derived units (such as the cubic metre and litre) or by various imperial or US customary units (such as the gallon, quart, cubic inch). The definition of length and height (cubed) is interrelated with volume. The volume of a container is generally understood to be the capacity of the container; i.e., the amount of fluid (gas or liquid) that the container could hold, rather than the amount of space the container itself displaces. By metonymy, the term "volume" sometimes is used to refer to the corresponding region (e.g., bounding volume). In ancient times, volume was measured using similar-shaped natural containers. Later on, standardized containers were used. Some simple three-dimensional shapes can have their volume easily calculated using arithmetic formulas. Volumes of more complicated shapes can be calculated with integral calculus if a formula exists for the shape ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
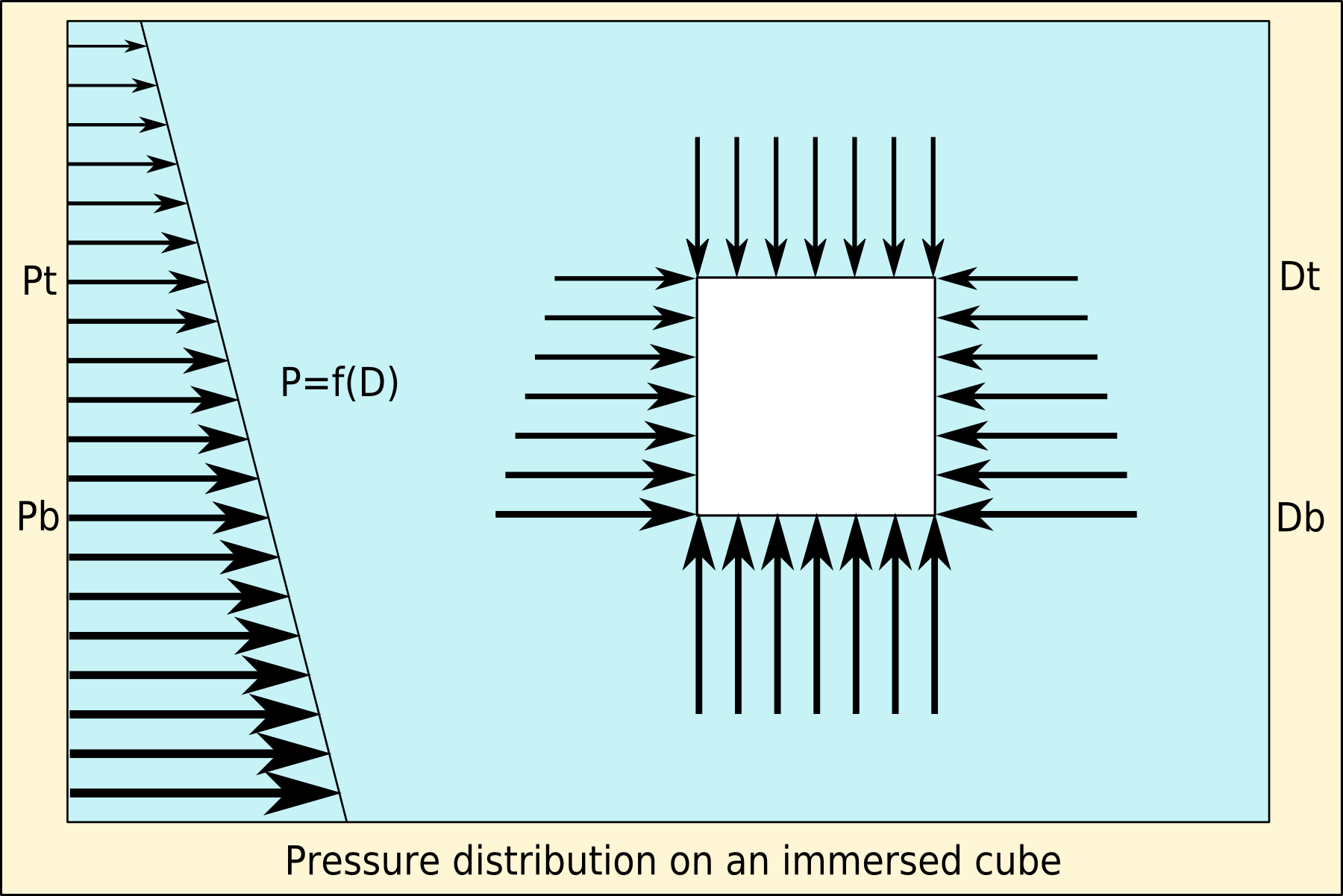
Archimedes' Principle
Archimedes' principle states that the upward buoyant force that is exerted on a body immersed in a fluid, whether fully or partially, is equal to the weight of the fluid that the body displaces. Archimedes' principle is a law of physics fundamental to fluid mechanics. It was formulated by Archimedes of Syracuse. Explanation In '' On Floating Bodies'', Archimedes suggested that (c. 246 BC): Archimedes' principle allows the buoyancy of any floating object partially or fully immersed in a fluid to be calculated. The downward force on the object is simply its weight. The upward, or buoyant, force on the object is that stated by Archimedes' principle above. Thus, the net force on the object is the difference between the magnitudes of the buoyant force and its weight. If this net force is positive, the object rises; if negative, the object sinks; and if zero, the object is neutrally buoyant—that is, it remains in place without either rising or sinking. In simple words, Archim ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Asymptotically
In analytic geometry, an asymptote () of a curve is a line such that the distance between the curve and the line approaches zero as one or both of the ''x'' or ''y'' coordinates tends to infinity. In projective geometry and related contexts, an asymptote of a curve is a line which is tangent to the curve at a point at infinity. The word asymptote is derived from the Greek ἀσύμπτωτος (''asumptōtos'') which means "not falling together", from ἀ priv. + σύν "together" + πτωτ-ός "fallen". The term was introduced by Apollonius of Perga in his work on conic sections, but in contrast to its modern meaning, he used it to mean any line that does not intersect the given curve. There are three kinds of asymptotes: ''horizontal'', ''vertical'' and ''oblique''. For curves given by the graph of a function , horizontal asymptotes are horizontal lines that the graph of the function approaches as ''x'' tends to Vertical asymptotes are vertical lines near which the fu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Oxford University Press
Oxford University Press (OUP) is the publishing house of the University of Oxford. It is the largest university press in the world. Its first book was printed in Oxford in 1478, with the Press officially granted the legal right to print books by decree in 1586. It is the second-oldest university press after Cambridge University Press, which was founded in 1534. It is a department of the University of Oxford. It is governed by a group of 15 academics, the Delegates of the Press, appointed by the Vice Chancellor, vice-chancellor of the University of Oxford. The Delegates of the Press are led by the Secretary to the Delegates, who serves as OUP's chief executive and as its major representative on other university bodies. Oxford University Press has had a similar governance structure since the 17th century. The press is located on Walton Street, Oxford, Walton Street, Oxford, opposite Somerville College, Oxford, Somerville College, in the inner suburb of Jericho, Oxford, Jericho. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Density
Density (volumetric mass density or specific mass) is the ratio of a substance's mass to its volume. The symbol most often used for density is ''ρ'' (the lower case Greek letter rho), although the Latin letter ''D'' (or ''d'') can also be used: \rho = \frac, where ''ρ'' is the density, ''m'' is the mass, and ''V'' is the volume. In some cases (for instance, in the United States oil and gas industry), density is loosely defined as its weight per unit volume, although this is scientifically inaccurate this quantity is more specifically called specific weight. For a pure substance, the density is equal to its mass concentration. Different materials usually have different densities, and density may be relevant to buoyancy, purity and packaging. Osmium is the densest known element at standard conditions for temperature and pressure. To simplify comparisons of density across different systems of units, it is sometimes replaced by the dimensionless quantity "relative den ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |