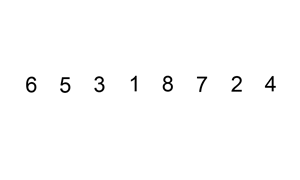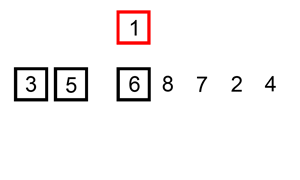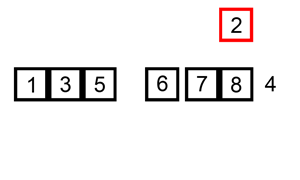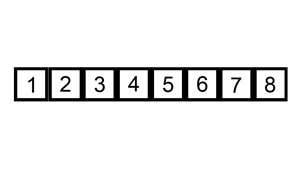|
Quicksort
Quicksort is an efficient, general-purpose sorting algorithm. Quicksort was developed by British computer scientist Tony Hoare in 1959 and published in 1961. It is still a commonly used algorithm for sorting. Overall, it is slightly faster than merge sort and heapsort for randomized data, particularly on larger distributions. Quicksort is a divide-and-conquer algorithm. It works by selecting a "pivot" element from the array and partitioning the other elements into two sub-arrays, according to whether they are less than or greater than the pivot. For this reason, it is sometimes called partition-exchange sort. The sub-arrays are then sorted recursively. This can be done in-place, requiring small additional amounts of memory to perform the sorting. Quicksort is a comparison sort, meaning that it can sort items of any type for which a "less-than" relation (formally, a total order) is defined. It is a comparison-based sort since elements ''a'' and ''b'' are only swapped in ca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sorting Algorithm
In computer science, a sorting algorithm is an algorithm that puts elements of a List (computing), list into an Total order, order. The most frequently used orders are numerical order and lexicographical order, and either ascending or descending. Efficient sorting is important for optimizing the Algorithmic efficiency, efficiency of other algorithms (such as search algorithm, search and merge algorithm, merge algorithms) that require input data to be in sorted lists. Sorting is also often useful for Canonicalization, canonicalizing data and for producing human-readable output. Formally, the output of any sorting algorithm must satisfy two conditions: # The output is in monotonic order (each element is no smaller/larger than the previous element, according to the required order). # The output is a permutation (a reordering, yet retaining all of the original elements) of the input. Although some algorithms are designed for sequential access, the highest-performing algorithms assum ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heapsort
In computer science, heapsort is an efficient, comparison-based sorting algorithm that reorganizes an input array into a heap (a data structure where each node is greater than its children) and then repeatedly removes the largest node from that heap, placing it at the end of the array in a similar manner to Selection sort. Although somewhat slower in practice on most machines than a well-implemented quicksort, it has the advantages of very simple implementation and a more favorable worst-case runtime. Most real-world quicksort variants include an implementation of heapsort as a fallback should they detect that quicksort is becoming degenerate. Heapsort is an in-place algorithm, but it is not a stable sort. Heapsort was invented by J. W. J. Williams in 1964. The paper also introduced the binary heap as a useful data structure in its own right. In the same year, Robert W. Floyd published an improved version that could sort an array in-place, continuing his earlier research ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Merge Sort
In computer science, merge sort (also commonly spelled as mergesort and as ) is an efficient, general-purpose, and comparison sort, comparison-based sorting algorithm. Most implementations of merge sort are Sorting algorithm#Stability, stable, which means that the relative order of equal elements is the same between the input and output. Merge sort is a divide-and-conquer algorithm that was invented by John von Neumann in 1945. A detailed description and analysis of bottom-up merge sort appeared in a report by Herman Goldstine, Goldstine and von Neumann as early as 1948. Algorithm Conceptually, a merge sort works as follows: #Divide the unsorted list into ''n'' sub-lists, each containing one element (a list of one element is considered sorted). #Repeatedly Merge algorithm, merge sublists to produce new sorted sublists until there is only one sublist remaining. This will be the sorted list. Top-down implementation Example C-like code using indices for top-down merge sort algorit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Samplesort
Samplesort is a sorting algorithm that is a divide and conquer algorithm often used in parallel processing systems. Conventional divide and conquer sorting algorithms partitions the array into sub-intervals or buckets. The buckets are then sorted individually and then concatenated together. However, if the array is non-uniformly distributed, the performance of these sorting algorithms can be significantly throttled. Samplesort addresses this issue by selecting a sample of size from the -element sequence, and determining the range of the buckets by sorting the sample and choosing elements from the result. These elements (called splitters) then divide the array into approximately equal-sized buckets. Samplesort is described in the 1970 paper, "Samplesort: A Sampling Approach to Minimal Storage Tree Sorting", by W. D. Frazer and A. C. McKellar. Algorithm Samplesort is a generalization of quicksort. Where quicksort partitions its input into two parts at each step, based on a single ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Divide-and-conquer Algorithm
In computer science, divide and conquer is an algorithm design paradigm. A divide-and-conquer algorithm recursively breaks down a problem into two or more sub-problems of the same or related type, until these become simple enough to be solved directly. The solutions to the sub-problems are then combined to give a solution to the original problem. The divide-and-conquer technique is the basis of efficient algorithms for many problems, such as sorting (e.g., quicksort, merge sort), multiplying large numbers (e.g., the Karatsuba algorithm), finding the closest pair of points, syntactic analysis (e.g., top-down parsers), and computing the discrete Fourier transform ( FFT). Designing efficient divide-and-conquer algorithms can be difficult. As in mathematical induction, it is often necessary to generalize the problem to make it amenable to a recursive solution. The correctness of a divide-and-conquer algorithm is usually proved by mathematical induction, and its computational cos ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
In-place Algorithm
In computer science, an in-place algorithm is an algorithm that operates directly on the input data structure without requiring extra space proportional to the input size. In other words, it modifies the input in place, without creating a separate copy of the data structure. An algorithm which is not in-place is sometimes called not-in-place or out-of-place. In-place can have slightly different meanings. In its strictest form, the algorithm can only have a constant amount of extra space, counting everything including function calls and pointers. However, this form is very limited as simply having an index to a length array requires bits. More broadly, in-place means that the algorithm does not use extra space for manipulating the input but may require a small though nonconstant extra space for its operation. Usually, this space is , though sometimes anything in is allowed. Note that space complexity also has varied choices in whether or not to count the index lengths as part ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Insertion Sort
Insertion sort is a simple sorting algorithm that builds the final sorted array (or list) one item at a time by comparisons. It is much less efficient on large lists than more advanced algorithms such as quicksort, heapsort, or merge sort. However, insertion sort provides several advantages: * Simple implementation: Jon Bentley shows a version that is three lines in C-like pseudo-code, and five lines when optimized. * Efficient for (quite) small data sets, much like other quadratic (i.e., O(''n''2)) sorting algorithms * More efficient in practice than most other simple quadratic algorithms such as selection sort or bubble sort * Adaptive, i.e., efficient for data sets that are already substantially sorted: the time complexity is O(''kn'') when each element in the input is no more than places away from its sorted position * Stable; i.e., does not change the relative order of elements with equal keys * In-place; i.e., only requires a constant amount O(1) of additional me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Qsort
qsort is a C standard library function that implements a sorting algorithm for arrays of arbitrary objects according to a user-provided comparison function. It is named after the "quicker sort" algorithm (a quicksort variant due to R. S. Scowen), which was originally used to implement it in the Unix C library, although the C standard does not require it to implement quicksort. The ability to operate on different kinds of data ('' polymorphism'') is achieved by taking a function pointer to a three-way comparison function, as well as a parameter that specifies the size of its individual input objects. The C standard requires the comparison function to implement a total order on the items in the input array. History A qsort function appears in Version 2 Unix in 1972 as a library assembly language subroutine. Its interface is unlike the modern version, in that it can be pseudo-prototyped as qsort(void * start, void * end, unsigned length) – sorting contiguously-stored length-l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shellsort
Shellsort, also known as Shell sort or Shell's method, is an in-place algorithm, in-place comparison sort. It can be understood as either a generalization of sorting by exchange (bubble sort) or sorting by insertion (insertion sort). The method starts by sorting pairs of elements far apart from each other, then progressively reducing the gap between elements to be compared. By starting with far-apart elements, it can move some out-of-place elements into the position faster than a simple nearest-neighbor exchange. The running time of Shellsort is heavily dependent on the gap sequence it uses. For many practical variants, determining their time complexity remains an open problem. The algorithm was first published by Donald Shell in 1959, and has nothing to do with shells. Description Shellsort is an optimization of insertion sort that allows the exchange of items that are far apart. The idea is to arrange the list of elements so that, starting anywhere, taking every ''h''th elem ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Robert Sedgewick (computer Scientist)
Robert Sedgewick (born December 20, 1946) is an American computer scientist. He is the founding chair and the William O. Baker Professor in Computer Science at Princeton University and was a member of the board of directors of Adobe Systems (1990–2016). He previously served on the faculty at Brown University and has held visiting research positions at Xerox PARC, Institute for Defense Analyses, and INRIA. His research expertise is in algorithm science, data structures, and analytic combinatorics. He is also active in developing college curriculums in computer science. Early life Sedgewick was born on December 20, 1946, in Willimantic, Connecticut. During his childhood he lived in Storrs, Connecticut, where his parents Charles Hill Wallace Sedgewick and Rose Whelan Sedgewick were professors at the University of Connecticut. In 1958, he moved with his parents to Wheaton, Maryland, a suburb of Washington, D.C., where he attended Wheaton High School, graduating in 1964. Ed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Analysis Of Algorithms
In computer science, the analysis of algorithms is the process of finding the computational complexity of algorithms—the amount of time, storage, or other resources needed to execute them. Usually, this involves determining a function that relates the size of an algorithm's input to the number of steps it takes (its time complexity) or the number of storage locations it uses (its space complexity). An algorithm is said to be efficient when this function's values are small, or grow slowly compared to a growth in the size of the input. Different inputs of the same size may cause the algorithm to have different behavior, so best, worst and average case descriptions might all be of practical interest. When not otherwise specified, the function describing the performance of an algorithm is usually an upper bound, determined from the worst case inputs to the algorithm. The term "analysis of algorithms" was coined by Donald Knuth. Algorithm analysis is an important part of a broa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |