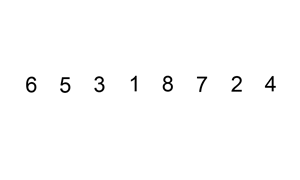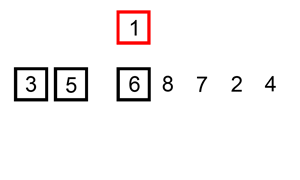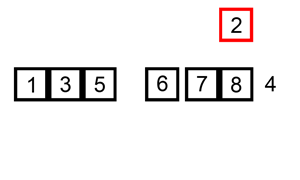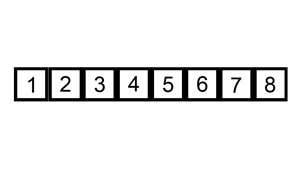|
Insertion Sort
Insertion sort is a simple sorting algorithm that builds the final sorted array (or list) one item at a time by comparisons. It is much less efficient on large lists than more advanced algorithms such as quicksort, heapsort, or merge sort. However, insertion sort provides several advantages: * Simple implementation: Jon Bentley shows a version that is three lines in C-like pseudo-code, and five lines when optimized. * Efficient for (quite) small data sets, much like other quadratic (i.e., O(''n''2)) sorting algorithms * More efficient in practice than most other simple quadratic algorithms such as selection sort or bubble sort * Adaptive, i.e., efficient for data sets that are already substantially sorted: the time complexity is O(''kn'') when each element in the input is no more than places away from its sorted position * Stable; i.e., does not change the relative order of elements with equal keys * In-place; i.e., only requires a constant amount O(1) of additional me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sorting Algorithm
In computer science, a sorting algorithm is an algorithm that puts elements of a List (computing), list into an Total order, order. The most frequently used orders are numerical order and lexicographical order, and either ascending or descending. Efficient sorting is important for optimizing the Algorithmic efficiency, efficiency of other algorithms (such as search algorithm, search and merge algorithm, merge algorithms) that require input data to be in sorted lists. Sorting is also often useful for Canonicalization, canonicalizing data and for producing human-readable output. Formally, the output of any sorting algorithm must satisfy two conditions: # The output is in monotonic order (each element is no smaller/larger than the previous element, according to the required order). # The output is a permutation (a reordering, yet retaining all of the original elements) of the input. Although some algorithms are designed for sequential access, the highest-performing algorithms assum ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
In-place Algorithm
In computer science, an in-place algorithm is an algorithm that operates directly on the input data structure without requiring extra space proportional to the input size. In other words, it modifies the input in place, without creating a separate copy of the data structure. An algorithm which is not in-place is sometimes called not-in-place or out-of-place. In-place can have slightly different meanings. In its strictest form, the algorithm can only have a constant amount of extra space, counting everything including function calls and pointers. However, this form is very limited as simply having an index to a length array requires bits. More broadly, in-place means that the algorithm does not use extra space for manipulating the input but may require a small though nonconstant extra space for its operation. Usually, this space is , though sometimes anything in is allowed. Note that space complexity also has varied choices in whether or not to count the index lengths as part ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Flash Memory
Flash memory is an Integrated circuit, electronic Non-volatile memory, non-volatile computer memory storage medium that can be electrically erased and reprogrammed. The two main types of flash memory, NOR flash and NAND flash, are named for the NOR gate, NOR and NAND gate, NAND logic gates. Both use the same cell design, consisting of floating-gate MOSFETs. They differ at the circuit level, depending on whether the state of the bit line or word lines is pulled high or low; in NAND flash, the relationship between the bit line and the word lines resembles a NAND gate; in NOR flash, it resembles a NOR gate. Flash memory, a type of floating-gate memory, was invented by Fujio Masuoka at Toshiba in 1980 and is based on EEPROM technology. Toshiba began marketing flash memory in 1987. EPROMs had to be erased completely before they could be rewritten. NAND flash memory, however, may be erased, written, and read in blocks (or pages), which generally are much smaller than the entire devi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
EEPROM
EEPROM or E2PROM (electrically erasable programmable read-only memory) is a type of non-volatile memory. It is used in computers, usually integrated in microcontrollers such as smart cards and remote keyless systems, or as a separate chip device, to store relatively small amounts of data by allowing individual bytes to be erased and reprogrammed. EEPROMs are organized as arrays of floating-gate transistors. EEPROMs can be programmed and erased in-circuit, by applying special programming signals. Originally, EEPROMs were limited to single-byte operations, which made them slower, but modern EEPROMs allow multi-byte page operations. An EEPROM has a limited life for erasing and reprogramming, reaching a million operations in modern EEPROMs. In an EEPROM that is frequently reprogrammed, the life of the EEPROM is an important design consideration. Flash memory is a type of EEPROM designed for high speed and high density, at the expense of large erase blocks (typically 512 b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bounds Checking
In computer programming, bounds checking is any method of detecting whether a variable is within some bounds before it is used. It is usually used to ensure that a number fits into a given type (range checking), or that a variable being used as an array index is within the bounds of the array (index checking). A failed bounds check usually results in the generation of some sort of exception signal. As performing bounds checking during each use can be time-consuming, it is not always done. Bounds-checking elimination is a compiler optimization technique that eliminates unneeded bounds checking. Range checking A range check is a check to make sure a number is within a certain range; for example, to ensure that a value about to be assigned to a 16-bit integer is within the capacity of a 16-bit integer (i.e. checking against wrap-around). This is not quite the same as type checking. Other range checks may be more restrictive; for example, a variable to hold the number of a calen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Short-circuit Evaluation
Short-circuit evaluation, minimal evaluation, or McCarthy evaluation (after John McCarthy) is the semantics of some Boolean operators in some programming languages in which the second argument is executed or evaluated only if the first argument does not suffice to determine the value of the expression: when the first argument of the AND function evaluates to false, the overall value must be false; and when the first argument of the OR function evaluates to true, the overall value must be true. In programming languages with lazy evaluation (Lisp, Perl, Haskell), the usual Boolean operators short-circuit. In others ( Ada, Java, Delphi), both short-circuit and standard Boolean operators are available. For some Boolean operations, like ''exclusive or'' (XOR), it is impossible to short-circuit, because both operands are always needed to determine a result. Short-circuit operators are, in effect, control structures rather than simple arithmetic operators, as they are not strict. I ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Invariant (computer Science)
In mathematics, an invariant is a property of a mathematical object (or a class of mathematical objects) which remains unchanged after operations or transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used. For example, the area of a triangle is an invariant with respect to isometries of the Euclidean plane. The phrases "invariant under" and "invariant to" a transformation are both used. More generally, an invariant with respect to an equivalence relation is a property that is constant on each equivalence class. Invariants are used in diverse areas of mathematics such as geometry, topology, algebra and discrete mathematics. Some important classes of transformations are defined by an invariant they leave unchanged. For example, conformal maps are defined as transformations of the plane that preserve angles. The discovery of invariants is an important ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zero-based Numbering
Zero-based numbering is a way of numbering in which the initial element of a sequence is assigned the index 0, rather than the index 1 as is typical in everyday non-mathematical or non-programming circumstances. Under zero-based numbering, the initial element is sometimes termed the '' zeroth'' element, rather than the ''first'' element; ''zeroth'' is a coined word for the ordinal number zero. In some cases, an object or value that does not (originally) belong to a given sequence, but which could be naturally placed before its initial element, may be termed the zeroth element. There is no wide agreement regarding the correctness of using zero as an ordinal (nor regarding the use of the term ''zeroth''), as it creates ambiguity for all subsequent elements of the sequence when lacking context. Numbering sequences starting at 0 is quite common in mathematics notation, in particular in combinatorics, though programming languages for mathematics usually index from 1. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pseudocode
In computer science, pseudocode is a description of the steps in an algorithm using a mix of conventions of programming languages (like assignment operator, conditional operator, loop) with informal, usually self-explanatory, notation of actions and conditions. Although pseudocode shares features with regular programming languages, it is intended for human reading rather than machine control. Pseudocode typically omits details that are essential for machine implementation of the algorithm, meaning that pseudocode can only be verified by hand. The programming language is augmented with natural language description details, where convenient, or with compact mathematical notation. The reasons for using pseudocode are that it is easier for people to understand than conventional programming language code and that it is an efficient and environment-independent description of the key principles of an algorithm. It is commonly used in textbooks and scientific publications to document ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Iteration
Iteration is the repetition of a process in order to generate a (possibly unbounded) sequence of outcomes. Each repetition of the process is a single iteration, and the outcome of each iteration is then the starting point of the next iteration. In mathematics and computer science, iteration (along with the related technique of recursion) is a standard element of algorithms. Mathematics In mathematics, iteration may refer to the process of iterated function, iterating a function, i.e. applying a function repeatedly, using the output from one iteration as the input to the next. Iteration of apparently simple functions can produce complex behaviors and difficult problems – for examples, see the Collatz conjecture and juggler sequences. Another use of iteration in mathematics is in iterative methods which are used to produce approximate numerical solutions to certain mathematical problems. Newton's method is an example of an iterative method. Manual calculation of a number's sq ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |