|
Orthonormal Basis
In mathematics, particularly linear algebra, an orthonormal basis for an inner product space V with finite Dimension (linear algebra), dimension is a Basis (linear algebra), basis for V whose vectors are orthonormal, that is, they are all unit vectors and Orthogonality_(mathematics), orthogonal to each other. For example, the standard basis for a Euclidean space \R^n is an orthonormal basis, where the relevant inner product is the dot product of vectors. The Image (mathematics), image of the standard basis under a Rotation (mathematics), rotation or Reflection (mathematics), reflection (or any orthogonal transformation) is also orthonormal, and every orthonormal basis for \R^n arises in this fashion. An orthonormal basis can be derived from an orthogonal basis via Normalize (linear algebra), normalization. The choice of an origin (mathematics), origin and an orthonormal basis forms a coordinate frame known as an ''orthonormal frame''. For a general inner product space V, an orthono ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orthogonality (mathematics)
In mathematics, orthogonality is the generalization of the geometric notion of ''perpendicularity'' to linear algebra of bilinear forms. Two elements and of a vector space with bilinear form B are orthogonal when B(\mathbf,\mathbf)= 0. Depending on the bilinear form, the vector space may contain null vectors, non-zero self-orthogonal vectors, in which case perpendicularity is replaced with hyperbolic orthogonality. In the case of function spaces, families of functions are used to form an orthogonal basis (linear algebra), basis, such as in the contexts of orthogonal polynomials, orthogonal functions, and combinatorics. Definitions * In geometry, two Euclidean vectors are orthogonal if they are perpendicular, ''i.e.'' they form a right angle. * Two vector space, vectors and in an inner product space V are ''orthogonal'' if their inner product \langle \mathbf, \mathbf \rangle is zero. This relationship is denoted \mathbf \perp \mathbf. * A set of vectors in an inner produ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orthogonal Transformation
In linear algebra, an orthogonal transformation is a linear transformation ''T'' : ''V'' → ''V'' on a real inner product space ''V'', that preserves the inner product. That is, for each pair of elements of ''V'', we have : \langle u,v \rangle = \langle Tu,Tv \rangle \, . Since the lengths of vectors and the angles between them are defined through the inner product, orthogonal transformations preserve lengths of vectors and angles between them. In particular, orthogonal transformations map orthonormal bases to orthonormal bases. Orthogonal transformations are injective: if Tv = 0 then 0 = \langle Tv,Tv \rangle = \langle v,v \rangle, hence v = 0, so the kernel of T is trivial. Orthogonal transformations in two- or three- dimensional Euclidean space are stiff rotations, reflections, or combinations of a rotation and a reflection (also known as improper rotations). Reflections are transformations that reverse the direction front to back, orthogonal to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dense Set
In topology and related areas of mathematics, a subset ''A'' of a topological space ''X'' is said to be dense in ''X'' if every point of ''X'' either belongs to ''A'' or else is arbitrarily "close" to a member of ''A'' — for instance, the rational numbers are a dense subset of the real numbers because every real number either is a rational number or has a rational number arbitrarily close to it (see Diophantine approximation). Formally, A is dense in X if the smallest closed subset of X containing A is X itself. The of a topological space X is the least cardinality of a dense subset of X. Definition A subset A of a topological space X is said to be a of X if any of the following equivalent conditions are satisfied: The smallest closed subset of X containing A is X itself. The closure of A in X is equal to X. That is, \operatorname_X A = X. The interior of the complement of A is empty. That is, \operatorname_X (X \setminus A) = \varnothing. Every point in X eith ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Span
In mathematics, the linear span (also called the linear hull or just span) of a set S of elements of a vector space V is the smallest linear subspace of V that contains S. It is the set of all finite linear combinations of the elements of , and the intersection of all linear subspaces that contain S. It is often denoted pp. 29-30, §§ 2.5, 2.8 or \langle S \rangle. For example, in geometry, two linearly independent vectors span a plane. To express that a vector space is a linear span of a subset , one commonly uses one of the following phrases: spans ; is a spanning set of ; is spanned or generated by ; is a generator set or a generating set of . Spans can be generalized to many mathematical structures, in which case, the smallest substructure containing S is generally called the substructure ''generated'' by S. Definition Given a vector space over a field , the span of a set of vectors (not necessarily finite) is defined to be the intersection of all subsp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hamel Basis
In mathematics, a set of elements of a vector space is called a basis (: bases) if every element of can be written in a unique way as a finite linear combination of elements of . The coefficients of this linear combination are referred to as components or coordinates of the vector with respect to . The elements of a basis are called . Equivalently, a set is a basis if its elements are linearly independent and every element of is a linear combination of elements of . In other words, a basis is a linearly independent spanning set. A vector space can have several bases; however all the bases have the same number of elements, called the dimension of the vector space. This article deals mainly with finite-dimensional vector spaces. However, many of the principles are also valid for infinite-dimensional vector spaces. Basis vectors find applications in the study of crystal structures and frames of reference. Definition A basis of a vector space over a field (such as t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Infinite Linear Combination
In mathematics, a linear combination or superposition is an expression constructed from a set of terms by multiplying each term by a constant and adding the results (e.g. a linear combination of ''x'' and ''y'' would be any expression of the form ''ax'' + ''by'', where ''a'' and ''b'' are constants). The concept of linear combinations is central to linear algebra and related fields of mathematics. Most of this article deals with linear combinations in the context of a vector space over a field, with some generalizations given at the end of the article. Definition Let ''V'' be a vector space over the field ''K''. As usual, we call elements of ''V'' ''vectors'' and call elements of ''K'' ''scalars''. If v1,...,v''n'' are vectors and ''a''1,...,''a''''n'' are scalars, then the ''linear combination of those vectors with those scalars as coefficients'' is :a_1 \mathbf v_1 + a_2 \mathbf v_2 + a_3 \mathbf v_3 + \cdots + a_n \mathbf v_n. There is some ambiguity in the use of the term "l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
McGraw-Hill
McGraw Hill is an American education science company that provides educational content, software, and services for students and educators across various levels—from K-12 to higher education and professional settings. They produce textbooks, digital learning tools, and adaptive technology to enhance learning experiences and outcomes. It is one of the "big three" educational publishers along with Houghton Mifflin Harcourt and Pearson Education. McGraw Hill also publishes reference and trade publications for the medical, business, and engineering professions. Formerly a division of The McGraw Hill Companies (later renamed McGraw Hill Financial, now S&P Global), McGraw Hill Education was divested and acquired by Apollo Global Management in March 2013 for $2.4 billion in cash. McGraw Hill was sold in 2021 to Platinum Equity for $4.5 billion. History McGraw Hill was founded in 1888, when James H. McGraw, co-founder of McGraw Hill, purchased the ''American Journal of Railway ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Functional Analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure (for example, Inner product space#Definition, inner product, Norm (mathematics)#Definition, norm, or Topological space#Definitions, topology) and the linear transformation, linear functions defined on these spaces and suitably respecting these structures. The historical roots of functional analysis lie in the study of function space, spaces of functions and the formulation of properties of transformations of functions such as the Fourier transform as transformations defining, for example, continuous function, continuous or unitary operator, unitary operators between function spaces. This point of view turned out to be particularly useful for the study of differential equations, differential and integral equations. The usage of the word ''functional (mathematics), functional'' as a noun goes back to the calculus of v ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
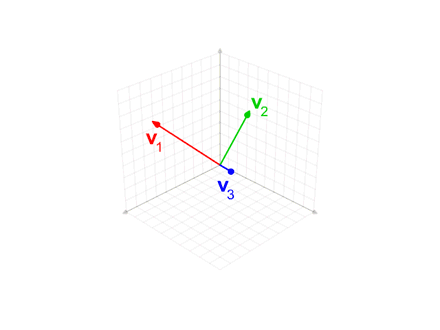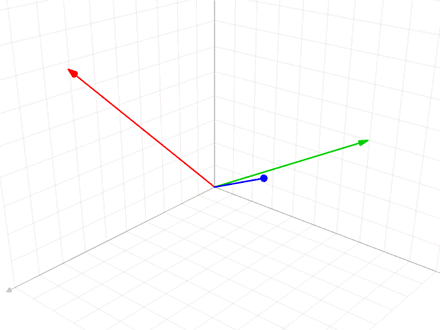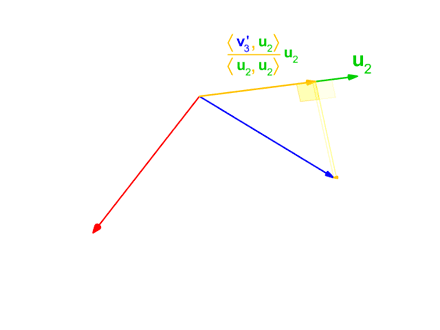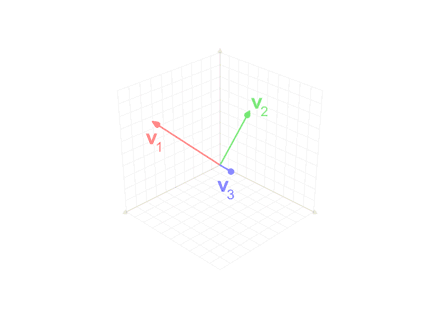
Gram–Schmidt Process
In mathematics, particularly linear algebra and numerical analysis, the Gram–Schmidt process or Gram-Schmidt algorithm is a way of finding a set of two or more vectors that are perpendicular to each other. By technical definition, it is a method of constructing an orthonormal basis from a set of vector (geometry), vectors in an inner product space, most commonly the Euclidean space \mathbb^n equipped with the standard inner product. The Gram–Schmidt process takes a finite set, finite, linearly independent set of vectors S = \ for and generates an orthogonal set S' = \ that spans the same k-dimensional subspace of \mathbb^n as S. The method is named after Jørgen Pedersen Gram and Erhard Schmidt, but Pierre-Simon Laplace had been familiar with it before Gram and Schmidt. In the theory of Lie group decompositions, it is generalized by the Iwasawa decomposition. The application of the Gram–Schmidt process to the column vectors of a full column rank (linear algebra), rank mat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dimension (vector Space)
In mathematics, the dimension of a vector space ''V'' is the cardinality (i.e., the number of vectors) of a Basis (linear algebra), basis of ''V'' over its base Field (mathematics), field. p. 44, §2.36 It is sometimes called Hamel dimension (after Georg Hamel) or algebraic dimension to distinguish it from other types of dimension. For every vector space there exists a basis, and all bases of a vector space have equal cardinality; as a result, the dimension of a vector space is uniquely defined. We say V is if the dimension of V is wiktionary:finite, finite, and if its dimension is infinity, infinite. The dimension of the vector space V over the field F can be written as \dim_F(V) or as [V : F], read "dimension of V over F". When F can be inferred from context, \dim(V) is typically written. Examples The vector space \R^3 has \left\ as a standard basis, and therefore \dim_(\R^3) = 3. More generally, \dim_(\R^n) = n, and even more generally, \dim_(F^n) = n for any Field (mathe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orthogonal Coordinates
In mathematics Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ..., orthogonal coordinates are defined as a set of coordinates \mathbf q = (q^1, q^2, \dots, q^d) in which the Coordinate system#Coordinate surface, coordinate hypersurfaces all meet at right angles (note that superscripts are Einstein notation, indices, not exponents). A coordinate surface for a particular coordinate is the curve, surface, or hypersurface on which is a constant. For example, the three-dimensional Cartesian coordinate system, Cartesian coordinates is an orthogonal coordinate system, since its coordinate surfaces constant, constant, and constant are planes that meet at right angles to one another, i.e., are perpendicular. Orthogonal coordinates are a special but extremely common case of curvilinear ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |