Gram–Schmidt Process

In mathematics, particularly linear algebra and numerical analysis, the Gram–Schmidt process or Gram-Schmidt algorithm is a way of finding a set of two or more vectors that are perpendicular to each other.

By technical definition, it is a method of constructing an orthonormal basis from a set of vectors in an inner product space, most commonly the Euclidean space $\mathbb^n$ equipped with the standard inner product. The Gram–Schmidt process takes a finite, linearly independent set of vectors $S = \$ for and generates an orthogonal set $S' = \$ that spans the same $k$-dimensional subspace of $\mathbb^n$ as $S$.

The method is named after Jørgen Pedersen Gram and Erhard Schmidt, but Pierre-Simon Laplace had been familiar with it before Gram and Schmidt. In the theory of Lie group decompositions, it is generalized by the Iwasawa decomposition.

The application of the Gram–Schmidt process to the column vectors of a full column rank matrix yields the QR decomposition (it is decomposed into an orthogonal and a triangular matrix).

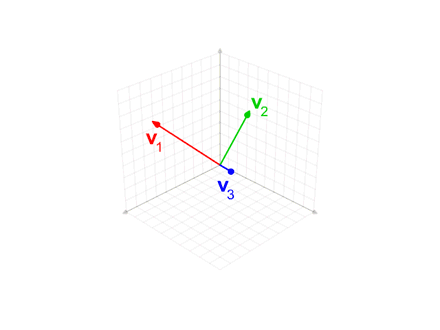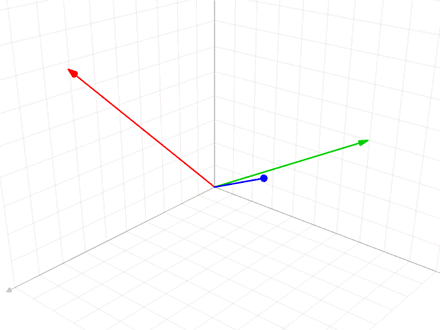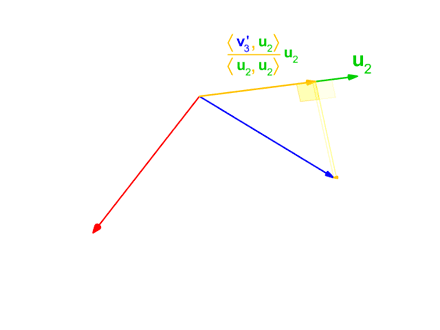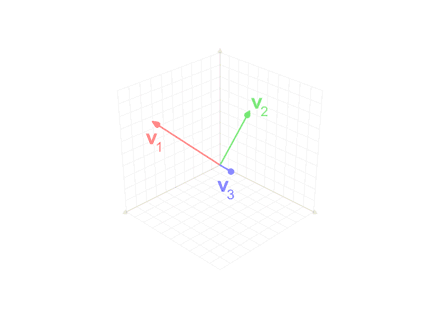
The Gram–Schmidt process

The vector projection of a vector $\mathbf v$ on a nonzero vector $\mathbf u$ is defined asIn the complex case, this assumes that the inner product is linear in the first argument and conjugate-linear in the second. In physics a more common convention is linearity in the second argument, in which case we define $\operatorname_ (\mathbf) = \frac \,\mathbf.$
$\operatorname_ (\mathbf) = \frac \,\mathbf ,$
where $\langle \mathbf, \mathbf\rangle$ denotes the inner product of the vectors $\mathbf u$ and $\mathbf v$. This means that $\operatorname_ (\mathbf)$ is the orthogonal projection of $\mathbf v$ onto the line spanned by $\mathbf u$. If $\mathbf u$ is the zero vector, then $\operatorname_ (\mathbf)$ is defined as the zero vector.

Given $k$ nonzero linearly-independent vectors $\mathbf_1, \ldots, \mathbf_k$ the Gram–Schmidt process defines the vectors $\mathbf_1, \ldots, \mathbf_k$ as follows:
$\begin \mathbf_1 & = \mathbf_1, & \!\mathbf_1 & = \frac \\ \mathbf_2 & = \mathbf_2-\operatorname_ (\mathbf_2), & \!\mathbf_2 & = \frac \\ \mathbf_3 & = \mathbf_3-\operatorname_ (\mathbf_3) - \operatorname_ (\mathbf_3), & \!\mathbf_3 & = \frac \\ \mathbf_4 & = \mathbf_4-\operatorname_ (\mathbf_4)-\operatorname_ (\mathbf_4)-\operatorname_ (\mathbf_4), & \!\mathbf_4 & = \\ & \ \ \vdots & & \ \ \vdots \\ \mathbf_k & = \mathbf_k - \sum_^\operatorname_ (\mathbf_k), & \!\mathbf_k & = \frac. \end$

The sequence $\mathbf_1, \ldots, \mathbf_k$ is the required system of orthogonal vectors, and the normalized vectors $\mathbf_1, \ldots, \mathbf_k$ form an orthonormal set. The calculation of the sequence $\mathbf_1, \ldots, \mathbf_k$ is known as ''Gram–Schmidt orthogonalization'', and the calculation of the sequence $\mathbf_1, \ldots, \mathbf_k$ is known as ''Gram–Schmidt orthonormalization''.

To check that these formulas yield an orthogonal sequence, first compute $\langle \mathbf_1, \mathbf_2 \rangle$ by substituting the above formula for $\mathbf_2$: we get zero. Then use this to compute $\langle \mathbf_1, \mathbf_3 \rangle$ again by substituting the formula for $\mathbf_3$: we get zero. For arbitrary $k$ the proof is accomplished by mathematical induction.

Geometrically, this method proceeds as follows: to compute $\mathbf_i$, it projects $\mathbf_i$ orthogonally onto the subspace $U$ generated by $\mathbf_1, \ldots, \mathbf_$, which is the same as the subspace generated by $\mathbf_1, \ldots, \mathbf_$. The vector $\mathbf_i$ is then defined to be the difference between $\mathbf_i$ and this projection, guaranteed to be orthogonal to all of the vectors in the subspace $U$.

The Gram–Schmidt process also applies to a linearly independent countably infinite sequence . The result is an orthogonal (or orthonormal) sequence such that for natural number : the algebraic span of $\mathbf_1, \ldots, \mathbf_$ is the same as that of $\mathbf_1, \ldots, \mathbf_$.

If the Gram–Schmidt process is applied to a linearly dependent sequence, it outputs the vector on the $i$th step, assuming that $\mathbf_i$ is a linear combination of $\mathbf_1, \ldots, \mathbf_$. If an orthonormal basis is to be produced, then the algorithm should test for zero vectors in the output and discard them because no multiple of a zero vector can have a length of 1. The number of vectors output by the algorithm will then be the dimension of the space spanned by the original inputs.

A variant of the Gram–Schmidt process using transfinite recursion applied to a (possibly uncountably) infinite sequence of vectors $(v_\alpha)_$ yields a set of orthonormal vectors $(u_\alpha)_$ with $\kappa\leq\lambda$ such that for any $\alpha\leq\lambda$, the completion of the span of $\$ is the same as that of In particular, when applied to a (algebraic) basis of a Hilbert space (or, more generally, a basis of any dense subspace), it yields a (functional-analytic) orthonormal basis. Note that in the general case often the strict inequality $\kappa < \lambda$ holds, even if the starting set was linearly independent, and the span of $(u_\alpha)_$ need not be a subspace of the span of $(v_\alpha)_$ (rather, it's a subspace of its completion).

Example

Euclidean space

Consider the following set of vectors in $\mathbb^2$ (with the conventional inner product)
$S = \left\.$

Now, perform Gram–Schmidt, to obtain an orthogonal set of vectors:
$\mathbf_1=\mathbf_1=\begin3\\1\end$
$\mathbf_2 = \mathbf_2 - \operatorname_ (\mathbf_2) = \begin2\\2\end - \operatorname_ = \begin2\\2\end - \frac \begin 3 \\1 \end = \begin -2/5 \\6/5 \end.$

We check that the vectors $\mathbf_1$ and $\mathbf_2$ are indeed orthogonal:
$\langle\mathbf_1,\mathbf_2\rangle = \left\langle \begin3\\1\end, \begin -2/5 \\ 6/5 \end \right\rangle = -\frac + \frac = 0,$
noting that if the dot product of two vectors is 0 then they are orthogonal.

For non-zero vectors, we can then normalize the vectors by dividing out their sizes as shown above:
$\mathbf_1 = \frac\begin3\\1\end$
$\mathbf_2 = \frac \begin-2/5\\6/5\end = \frac \begin-1\\3\end.$

Properties

Denote by $\operatorname(\mathbf_1, \dots, \mathbf_k)$ the result of applying the Gram–Schmidt process to a collection of vectors $\mathbf_1, \dots, \mathbf_k$. This yields a map $\operatorname \colon (\R^n)^ \to (\R^n)^$.

It has the following properties:

* It is continuous
* It is orientation preserving in the sense that $\operatorname(\mathbf_1,\dots,\mathbf_k) = \operatorname(\operatorname(\mathbf_1,\dots,\mathbf_k))$.
* It commutes with orthogonal maps:

Let $g \colon \R^n \to \R^n$ be orthogonal (with respect to the given inner product). Then we have
$\operatorname(g(\mathbf_1),\dots,g(\mathbf_k)) = \left( g(\operatorname(\mathbf_1,\dots,\mathbf_k)_1),\dots,g(\operatorname(\mathbf_1,\dots,\mathbf_k)_k) \right)$

Further, a parametrized version of the Gram–Schmidt process yields a (strong) deformation retraction of the general linear group $\mathrm(\R^n)$ onto the orthogonal group $O(\R^n)$.

Numerical stability

When this process is implemented on a computer, the vectors $\mathbf_k$ are often not quite orthogonal, due to rounding errors. For the Gram–Schmidt process as described above (sometimes referred to as "classical Gram–Schmidt") this loss of orthogonality is particularly bad; therefore, it is said that the (classical) Gram–Schmidt process is numerically unstable.

The Gram–Schmidt process can be stabilized by a small modification; this version is sometimes referred to as modified Gram-Schmidt or MGS. This approach gives the same result as the original formula in exact arithmetic and introduces smaller errors in finite-precision arithmetic.

Instead of computing the vector as
$\mathbf_k = \mathbf_k - \operatorname_ (\mathbf_k) - \operatorname_ (\mathbf_k) - \cdots - \operatorname_ (\mathbf_k),$
it is computed as
$\begin \mathbf_k^ &= \mathbf_k - \operatorname_ (\mathbf_k), \\ \mathbf_k^ &= \mathbf_k^ - \operatorname_ \left(\mathbf_k^\right), \\ & \;\; \vdots \\ \mathbf_k^ &= \mathbf_k^ - \operatorname_ \left(\mathbf_k^\right), \\ \mathbf_k^ &= \mathbf_k^ - \operatorname_ \left(\mathbf_k^\right), \\ \mathbf_k &= \frac \end$

This method is used in the previous animation, when the intermediate $\mathbf'_3$ vector is used when orthogonalizing the blue vector $\mathbf_3$.

Here is another description of the modified algorithm. Given the vectors $\mathbf_1, \mathbf_2, \dots, \mathbf_n$, in our first step we produce vectors $\mathbf_1, \mathbf_2^, \dots, \mathbf_n^$by removing components along the direction of $\mathbf_1$. In formulas, $\mathbf_k^ := \mathbf_k - \frac \mathbf_1$. After this step we already have two of our desired orthogonal vectors $\mathbf_1, \dots, \mathbf_n$, namely $\mathbf_1 = \mathbf_1, \mathbf_2 = \mathbf_2^$, but we also made $\mathbf_3^, \dots, \mathbf_n^$ already orthogonal to $\mathbf_1$. Next, we orthogonalize those remaining vectors against $\mathbf_2 = \mathbf_2^$. This means we compute $\mathbf_3^, \mathbf_4^, \dots, \mathbf_n^$ by subtraction $\mathbf_k^ := \mathbf_k^ - \frac \mathbf_2$. Now we have stored the vectors $\mathbf_1, \mathbf_2^, \mathbf_3^, \mathbf_4^, \dots, \mathbf_n^$ where the first three vectors are already $\mathbf_1, \mathbf_2, \mathbf_3$ and the remaining vectors are already orthogonal to $\mathbf_1, \mathbf_2$. As should be clear now, the next step orthogonalizes $\mathbf_4^, \dots, \mathbf_n^$ against $\mathbf_3 = \mathbf_3^$. Proceeding in this manner we find the full set of orthogonal vectors $\mathbf_1, \dots, \mathbf_n$. If orthonormal vectors are desired, then we normalize as we go, so that the denominators in the subtraction formulas turn into ones.

Algorithm

The following MATLAB algorithm implements classical Gram–Schmidt orthonormalization. The vectors (columns of matrix V, so that V(:,j) is the $j$th vector) are replaced by orthonormal vectors (columns of U) which span the same subspace.

function U = gramschmidt(V)
, k= size(V);
U = zeros(n,k);
U(:,1) = V(:,1) / norm(V(:,1));
for i = 2:k
U(:,i) = V(:,i);
for j = 1:i-1
U(:,i) = U(:,i) - (U(:,j)'*U(:,i)) * U(:,j);
end
U(:,i) = U(:,i) / norm(U(:,i));
end
end

The cost of this algorithm is asymptotically floating point operations, where is the dimensionality of the vectors.

Via Gaussian elimination

If the rows are written as a matrix $A$, then applying Gaussian elimination to the augmented matrix \left A \right/math> will produce the orthogonalized vectors in place of $A$. However the matrix $A A^\mathsf$ must be brought to row echelon form, using only the row operation of adding a scalar multiple of one row to another. For example, taking $\mathbf_1 = \begin 3 & 1\end, \mathbf_2=\begin2 & 2\end$ as above, we have
\left A \right= \left begin 10 & 8 & 3 & 1 \\ 8 & 8 & 2 & 2\end\right/math>

And reducing this to row echelon form produces
\left begin 1 & .8 & .3 & .1 \\ 0 & 1 & -.25 & .75\end\right/math>

The normalized vectors are then
$\mathbf_1 = \frac\begin.3 & .1\end = \frac \begin3 & 1\end$
$\mathbf_2 = \frac \begin-.25 & .75\end = \frac \begin-1 & 3\end,$
as in the example above.

Determinant formula

The result of the Gram–Schmidt process may be expressed in a non-recursive formula using determinants.

$\mathbf_j = \frac \begin \langle \mathbf_1, \mathbf_1 \rangle & \langle \mathbf_2, \mathbf_1 \rangle & \cdots & \langle \mathbf_j, \mathbf_1 \rangle \\ \langle \mathbf_1, \mathbf_2 \rangle & \langle \mathbf_2, \mathbf_2 \rangle & \cdots & \langle \mathbf_j, \mathbf_2 \rangle \\ \vdots & \vdots & \ddots & \vdots \\ \langle \mathbf_1, \mathbf_ \rangle & \langle \mathbf_2, \mathbf_ \rangle & \cdots & \langle \mathbf_j, \mathbf_ \rangle \\ \mathbf_1 & \mathbf_2 & \cdots & \mathbf_j \end$

$\mathbf_j = \frac \begin \langle \mathbf_1, \mathbf_1 \rangle & \langle \mathbf_2, \mathbf_1 \rangle & \cdots & \langle \mathbf_j, \mathbf_1 \rangle \\ \langle \mathbf_1, \mathbf_2 \rangle & \langle \mathbf_2, \mathbf_2 \rangle & \cdots & \langle \mathbf_j, \mathbf_2 \rangle \\ \vdots & \vdots & \ddots & \vdots \\ \langle \mathbf_1, \mathbf_ \rangle & \langle \mathbf_2, \mathbf_ \rangle & \cdots & \langle \mathbf_j, \mathbf_ \rangle \\ \mathbf_1 & \mathbf_2 & \cdots & \mathbf_j \end$

where $D_0 = 1$ and, for $j \ge 1$, $D_j$ is the Gram determinant

$D_j = \begin \langle \mathbf_1, \mathbf_1 \rangle & \langle \mathbf_2, \mathbf_1 \rangle & \cdots & \langle \mathbf_j, \mathbf_1 \rangle \\ \langle \mathbf_1, \mathbf_2 \rangle & \langle \mathbf_2, \mathbf_2 \rangle & \cdots & \langle \mathbf_j, \mathbf_2 \rangle \\ \vdots & \vdots & \ddots & \vdots \\ \langle \mathbf_1, \mathbf_j \rangle & \langle \mathbf_2, \mathbf_j \rangle & \cdots & \langle \mathbf_j, \mathbf_j \rangle \end.$

Note that the expression for $\mathbf_k$ is a "formal" determinant, i.e. the matrix contains both scalars and vectors; the meaning of this expression is defined to be the result of a cofactor expansion along the row of vectors.

The determinant formula for the Gram-Schmidt is computationally (exponentially) slower than the recursive algorithms described above; it is mainly of theoretical interest.

Expressed using geometric algebra

Expressed using notation used in geometric algebra, the unnormalized results of the Gram–Schmidt process can be expressed as
$\mathbf_k = \mathbf_k - \sum_^ (\mathbf_k \cdot \mathbf_j)\mathbf_j^\ ,$
which is equivalent to the expression using the $\operatorname$ operator defined above. The results can equivalently be expressed as
$\mathbf_k = \mathbf_\wedge\mathbf_\wedge\cdot\cdot\cdot\wedge\mathbf_(\mathbf_\wedge\cdot\cdot\cdot\wedge\mathbf_)^,$
which is closely related to the expression using determinants above.

Alternatives

Other orthogonalization algorithms use Householder transformations or Givens rotations. The algorithms using Householder transformations are more stable than the stabilized Gram–Schmidt process. On the other hand, the Gram–Schmidt process produces the $j$th orthogonalized vector after the $j$th iteration, while orthogonalization using Householder reflections produces all the vectors only at the end. This makes only the Gram–Schmidt process applicable for iterative methods like the Arnoldi iteration.

Yet another alternative is motivated by the use of Cholesky decomposition for inverting the matrix of the normal equations in linear least squares. Let $V$ be a full column rank matrix, whose columns need to be orthogonalized. The matrix $V^* V$ is Hermitian and positive definite, so it can be written as $V^* V = L L^*,$ using the Cholesky decomposition. The lower triangular matrix $L$ with strictly positive diagonal entries is invertible. Then columns of the matrix $U = V\left(L^\right)^*$ are orthonormal and span the same subspace as the columns of the original matrix $V$. The explicit use of the product $V^* V$ makes the algorithm unstable, especially if the product's condition number is large. Nevertheless, this algorithm is used in practice and implemented in some software packages because of its high efficiency and simplicity.

In quantum mechanics there are several orthogonalization schemes with characteristics better suited for certain applications than original Gram–Schmidt. Nevertheless, it remains a popular and effective algorithm for even the largest electronic structure calculations.

Run-time complexity

Gram-Schmidt orthogonalization can be done in strongly-polynomial time. The run-time analysis is similar to that of Gaussian elimination.

See also

* Linear algebra
* Recursion
* Orthogonality (mathematics)

References

Notes

Sources

* .
* .
* .
* .

External links

*

Harvey Mudd College Math Tutorial on the Gram-Schmidt algorithm


The entry "Gram-Schmidt orthogonalization" has some information and references on the origins of the method.
* Demos
Gram Schmidt process in plane
an
Gram Schmidt process in space




* Proof: ttp://planetmath.org/ProofOfGramSchmidtOrthogonalizationProcedure Raymond Puzio, Keenan Kidwell. "proof of Gram-Schmidt orthogonalization algorithm" (version 8). PlanetMath.org.

{{DEFAULTSORT:Gram-Schmidt Process
Linear algebra
Functional analysis
Articles with example MATLAB/Octave code