|
Morton Number
: In fluid dynamics, the Morton number (Mo) is a dimensionless number used together with the Eötvös number or Bond number to characterize the shape of bubbles or drops moving in a surrounding fluid or continuous phase, ''c''. It is named after Rose Morton, who described it with W. L. Haberman in 1953. Definition The Morton number is defined as : \mathrm = \frac, where ''g'' is the acceleration of gravity, \mu_c is the viscosity of the surrounding fluid, \rho_c the density of the surrounding fluid, \Delta \rho the difference in density of the phases, and \sigma is the surface tension coefficient. For the case of a bubble with a negligible inner density the Morton number can be simplified to :\mathrm = \frac. Relation to other parameters The Morton number can also be expressed by using a combination of the Weber number, Froude number and Reynolds number In fluid mechanics, the Reynolds number () is a dimensionless quantity that helps predict fluid flow patterns in d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fluid Dynamics
In physics and engineering, fluid dynamics is a subdiscipline of fluid mechanics that describes the flow of fluids—liquids and gases. It has several subdisciplines, including '' aerodynamics'' (the study of air and other gases in motion) and hydrodynamics (the study of liquids in motion). Fluid dynamics has a wide range of applications, including calculating forces and moments on aircraft, determining the mass flow rate of petroleum through pipelines, predicting weather patterns, understanding nebulae in interstellar space and modelling fission weapon detonation. Fluid dynamics offers a systematic structure—which underlies these practical disciplines—that embraces empirical and semi-empirical laws derived from flow measurement and used to solve practical problems. The solution to a fluid dynamics problem typically involves the calculation of various properties of the fluid, such as flow velocity, pressure, density, and temperature, as functions of space a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dimensionless Number
A dimensionless quantity (also known as a bare quantity, pure quantity, or scalar quantity as well as quantity of dimension one) is a quantity to which no physical dimension is assigned, with a corresponding SI unit of measurement of one (or 1), ISBN 978-92-822-2272-0. which is not explicitly shown. Dimensionless quantities are widely used in many fields, such as mathematics, physics, chemistry, engineering, and economics. Dimensionless quantities are distinct from quantities that have associated dimensions, such as time (measured in seconds). Dimensionless units are dimensionless values that serve as units of measurement for expressing other quantities, such as radians (rad) or steradians (sr) for plane angles and solid angles, respectively. For example, optical extent is defined as having units of metres multiplied by steradians. History Quantities having dimension one, ''dimensionless quantities'', regularly occur in sciences, and are formally treated within the fie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eötvös Number
In fluid dynamics the Eötvös number (Eo), also called the Bond number (Bo), is a dimensionless number measuring the importance of gravitational forces compared to surface tension forces for the movement of liquid front. Alongside the Capillary number, commonly denoted Ca, which represents the contribution of viscous drag, Bo is useful for studying the movement of fluid in porous or granular media, such as soil.Dynamics of viscous entrapped saturated zones in partially wetted porous media Transport in Porous Media (2018), 125(2), 193-210 The Bond number (or Eötvös number) is also used (together with Morton number) to characterize the shape of [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rose Morton
Rose Katherine Morton-Sayre (December 3, 1925 – November 12, 1999) was an American mathematician known for her work in fluid mechanics. The Morton number, a dimensionless parameter used to describe bubbles, is named after her. Morton was born in Albemarle, North Carolina. She graduated from the University of North Carolina at Greensboro (at that time a women's college) with a bachelor's degree in mathematics in 1948; at the university, she was president of the Square Circle Club. She worked at the David Taylor Model Basin The David Taylor Model Basin (DTMB) is one of the largest ship model basins—test facilities for the development of ship design—in the world. DTMB is a field activity of the Carderock Division of the Naval Surface Warfare Center. Hist ..., a test facility for the U. S. Navy, from 1949 to 1960. Her husband was mechanical engineer Clifford L. Sayre, Jr., who also worked at the David Taylor Model Basin from 1956 to 1960. Selected publications ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Viscosity
The viscosity of a fluid is a measure of its resistance to deformation at a given rate. For liquids, it corresponds to the informal concept of "thickness": for example, syrup has a higher viscosity than water. Viscosity quantifies the internal frictional force between adjacent layers of fluid that are in relative motion. For instance, when a viscous fluid is forced through a tube, it flows more quickly near the tube's axis than near its walls. Experiments show that some stress (such as a pressure difference between the two ends of the tube) is needed to sustain the flow. This is because a force is required to overcome the friction between the layers of the fluid which are in relative motion. For a tube with a constant rate of flow, the strength of the compensating force is proportional to the fluid's viscosity. In general, viscosity depends on a fluid's state, such as its temperature, pressure, and rate of deformation. However, the dependence on some of these properties ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Density
Density (volumetric mass density or specific mass) is the substance's mass per unit of volume. The symbol most often used for density is ''ρ'' (the lower case Greek letter rho), although the Latin letter ''D'' can also be used. Mathematically, density is defined as mass divided by volume: : \rho = \frac where ''ρ'' is the density, ''m'' is the mass, and ''V'' is the volume. In some cases (for instance, in the United States oil and gas industry), density is loosely defined as its weight per unit volume, although this is scientifically inaccurate – this quantity is more specifically called specific weight. For a pure substance the density has the same numerical value as its mass concentration. Different materials usually have different densities, and density may be relevant to buoyancy, purity and packaging. Osmium and iridium are the densest known elements at standard conditions for temperature and pressure. To simplify comparisons of density across different syst ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Surface Tension
Surface tension is the tendency of liquid surfaces at rest to shrink into the minimum surface area possible. Surface tension is what allows objects with a higher density than water such as razor blades and insects (e.g. water striders) to float on a water surface without becoming even partly submerged. At liquid–air interfaces, surface tension results from the greater attraction of liquid molecules to each other (due to cohesion) than to the molecules in the air (due to adhesion). There are two primary mechanisms in play. One is an inward force on the surface molecules causing the liquid to contract. Second is a tangential force parallel to the surface of the liquid. This ''tangential'' force is generally referred to as the surface tension. The net effect is the liquid behaves as if its surface were covered with a stretched elastic membrane. But this analogy must not be taken too far as the tension in an elastic membrane is dependent on the amount of deformation of th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Weber Number
The Weber number (We) is a dimensionless number in fluid mechanics that is often useful in analysing fluid flows where there is an interface between two different fluids, especially for multiphase flows with strongly curved surfaces. It is named after Moritz Weber (1871–1951). It can be thought of as a measure of the relative importance of the fluid's inertia compared to its surface tension. The quantity is useful in analyzing thin film flows and the formation of droplets and bubbles. Mathematical expression The Weber number may be written as: :\mathrm = \frac = \left( \frac \right) \frac = \frac where * C_\mathrm is the drag coefficient of the body cross-section. * \rho is the density of the fluid ( kg/ m3). * v is its velocity (m/ s). * l is its characteristic length Length is a measure of distance. In the International System of Quantities, length is a quantity with dimension distance. In most systems of measurement a base unit for length is chosen, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
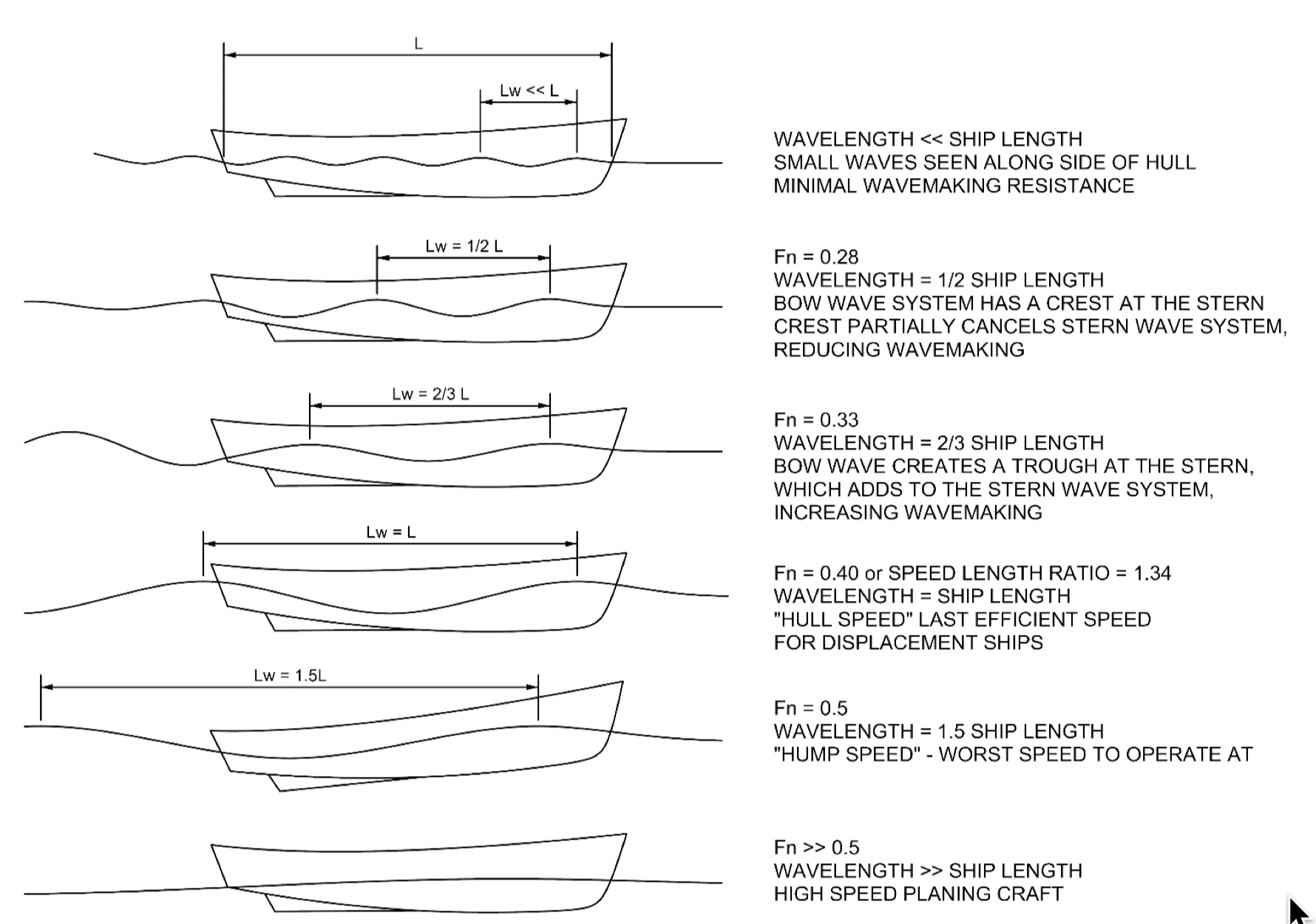
Froude Number
In continuum mechanics, the Froude number (, after William Froude, ) is a dimensionless number defined as the ratio of the flow inertia to the external field (the latter in many applications simply due to gravity). The Froude number is based on the speed–length ratio which he defined as: \mathrm = \frac where is the local flow velocity, is the local external field, and is a characteristic length. The Froude number has some analogy with the Mach number. In theoretical fluid dynamics the Froude number is not frequently considered since usually the equations are considered in the high Froude limit of negligible external field, leading to homogeneous equations that preserve the mathematical aspects. For example, homogeneous Euler equations are conservation equations. However, in naval architecture the Froude number is a significant figure used to determine the resistance of a partially submerged object moving through water. Origins In open channel flows, introduced first ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reynolds Number
In fluid mechanics, the Reynolds number () is a dimensionless quantity that helps predict fluid flow patterns in different situations by measuring the ratio between inertial and viscous forces. At low Reynolds numbers, flows tend to be dominated by laminar (sheet-like) flow, while at high Reynolds numbers flows tend to be turbulent. The turbulence results from differences in the fluid's speed and direction, which may sometimes intersect or even move counter to the overall direction of the flow (eddy currents). These eddy currents begin to churn the flow, using up energy in the process, which for liquids increases the chances of cavitation. The Reynolds number has wide applications, ranging from liquid flow in a pipe to the passage of air over an aircraft wing. It is used to predict the transition from laminar to turbulent flow and is used in the scaling of similar but different-sized flow situations, such as between an aircraft model in a wind tunnel and the full-size ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equivalent Spherical Diameter
The equivalent spherical diameter of an irregularly shaped object is the diameter of a sphere of equivalent geometric, optical, electrical, aerodynamic or hydrodynamic behavior to that of the particle under investigation. The particle size of a perfectly smooth, spherical object can be accurately defined by a single parameter, the particle diameter. However, real-life particles are likely to have irregular shapes and surface irregularities, and their size cannot be fully characterized by a single parameter. The concept of equivalent spherical diameter has been introduced in the field of particle size analysis to enable the representation of the particle size distribution in a simplified, homogenized way. Here, the real-life particle is matched with an imaginary sphere which has the same properties according to a defined principle, enabling the real-life particle to be defined by the diameter of the imaginary sphere. The principle used to match the real-life particle and the ima ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dimensionless Numbers
A dimensionless quantity (also known as a bare quantity, pure quantity, or scalar quantity as well as quantity of dimension one) is a quantity to which no physical dimension is assigned, with a corresponding SI unit of measurement of one (or 1), ISBN 978-92-822-2272-0. which is not explicitly shown. Dimensionless quantities are widely used in many fields, such as mathematics, physics, chemistry, engineering, and economics. Dimensionless quantities are distinct from quantities that have associated dimensions, such as time (measured in seconds). Dimensionless units are dimensionless values that serve as units of measurement for expressing other quantities, such as radians (rad) or steradians (sr) for plane angles and solid angles, respectively. For example, optical extent is defined as having units of metres multiplied by steradians. History Quantities having dimension one, ''dimensionless quantities'', regularly occur in sciences, and are formally treated within the field ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |


.jpg)