|
Material Derivative
In continuum mechanics, the material derivative describes the time rate of change of some physical quantity (like heat or momentum) of a material element that is subjected to a space-and-time-dependent macroscopic velocity field. The material derivative can serve as a link between Eulerian and Lagrangian descriptions of continuum deformation. For example, in fluid dynamics, the velocity field is the flow velocity, and the quantity of interest might be the temperature of the fluid. In this case, the material derivative then describes the temperature change of a certain fluid parcel with time, as it flows along its pathline (trajectory). Other names There are many other names for the material derivative, including: *advective derivative *convective derivative *derivative following the motion *hydrodynamic derivative *Lagrangian derivative *particle derivative *substantial derivative *substantive derivative *Stokes derivative *total derivative, although the material derivati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
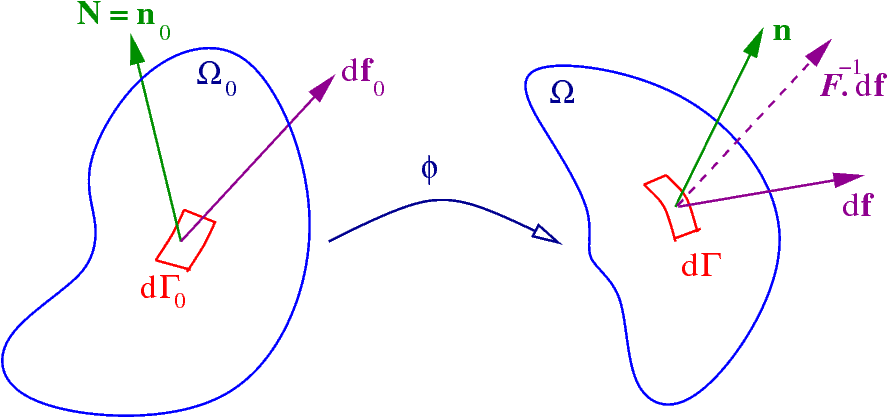
Continuum Mechanics
Continuum mechanics is a branch of mechanics that deals with the deformation of and transmission of forces through materials modeled as a ''continuous medium'' (also called a ''continuum'') rather than as discrete particles. Continuum mechanics deals with ''deformable bodies'', as opposed to rigid bodies. A continuum model assumes that the substance of the object completely fills the space it occupies. While ignoring the fact that matter is made of atoms, this provides a sufficiently accurate description of matter on length scales much greater than that of inter-atomic distances. The concept of a continuous medium allows for intuitive analysis of bulk matter by using differential equations that describe the behavior of such matter according to physical laws, such as mass conservation, momentum conservation, and energy conservation. Information about the specific material is expressed in constitutive relationships. Continuum mechanics treats the physical properties of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tensor Derivative (continuum Mechanics)
The derivatives of scalars, vectors, and second-order tensors with respect to second-order tensors are of considerable use in continuum mechanics. These derivatives are used in the theories of nonlinear elasticity and plasticity, particularly in the design of algorithms for numerical simulations. The directional derivative provides a systematic way of finding these derivatives. Derivatives with respect to vectors and second-order tensors The definitions of directional derivatives for various situations are given below. It is assumed that the functions are sufficiently smooth that derivatives can be taken. Derivatives of scalar valued functions of vectors Let ''f''(v) be a real valued function of the vector v. Then the derivative of ''f''(v) with respect to v (or at v) is the vector defined through its dot product with any vector u being \frac\cdot\mathbf = Df(\mathbf) mathbf= \left frac~f(\mathbf + \alpha~\mathbf)\right for all vectors u. The above dot product yields a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orthogonal Coordinates
In mathematics Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ..., orthogonal coordinates are defined as a set of coordinates \mathbf q = (q^1, q^2, \dots, q^d) in which the Coordinate system#Coordinate surface, coordinate hypersurfaces all meet at right angles (note that superscripts are Einstein notation, indices, not exponents). A coordinate surface for a particular coordinate is the curve, surface, or hypersurface on which is a constant. For example, the three-dimensional Cartesian coordinate system, Cartesian coordinates is an orthogonal coordinate system, since its coordinate surfaces constant, constant, and constant are planes that meet at right angles to one another, i.e., are perpendicular. Orthogonal coordinates are a special but extremely common case of curvilinear ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Upper Convected Time Derivative
In continuum mechanics, including fluid dynamics, an upper-convected time derivative or Oldroyd derivative, named after James G. Oldroyd, is the rate of change of some tensor property of a small parcel of fluid that is written in the coordinate system rotating and stretching with the fluid. The operator is specified by the following formula: : \stackrel = \frac \mathbf - (\nabla \mathbf)^T \cdot \mathbf - \mathbf \cdot (\nabla \mathbf) where: * is the upper-convected time derivative of a tensor field \mathbf *\frac is the substantive derivative *\nabla \mathbf=\frac is the tensor of velocity derivatives for the fluid. The formula can be rewritten as: : _ = \frac + v_k \frac - \frac A_ - \frac A_ By definition, the upper-convected time derivative of the Finger tensor is always zero. It can be shown that the upper-convected time derivative of a spacelike vector field is just its Lie derivative by the velocity field of the continuum. The upper-convected derivat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tensor
In mathematics, a tensor is an algebraic object that describes a multilinear relationship between sets of algebraic objects associated with a vector space. Tensors may map between different objects such as vectors, scalars, and even other tensors. There are many types of tensors, including scalars and vectors (which are the simplest tensors), dual vectors, multilinear maps between vector spaces, and even some operations such as the dot product. Tensors are defined independent of any basis, although they are often referred to by their components in a basis related to a particular coordinate system; those components form an array, which can be thought of as a high-dimensional matrix. Tensors have become important in physics because they provide a concise mathematical framework for formulating and solving physics problems in areas such as mechanics ( stress, elasticity, quantum mechanics, fluid mechanics, moment of inertia, ...), electrodynamics ( electromagnetic ten ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant (as opposed to the total derivative, in which all variables are allowed to vary). Partial derivatives are used in vector calculus and differential geometry. The partial derivative of a function f(x, y, \dots) with respect to the variable x is variously denoted by It can be thought of as the rate of change of the function in the x-direction. Sometimes, for the partial derivative of z with respect to x is denoted as \tfrac. Since a partial derivative generally has the same arguments as the original function, its functional dependence is sometimes explicitly signified by the notation, such as in: f'_x(x, y, \ldots), \frac (x, y, \ldots). The symbol used to denote partial derivatives is ∂. One of the first known uses of this symbol in mathematics is by Marquis de Condorcet from 1770, who used it for partial differ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chain Rule
In calculus, the chain rule is a formula that expresses the derivative of the Function composition, composition of two differentiable functions and in terms of the derivatives of and . More precisely, if h=f\circ g is the function such that h(x)=f(g(x)) for every , then the chain rule is, in Lagrange's notation, h'(x) = f'(g(x)) g'(x). or, equivalently, h'=(f\circ g)'=(f'\circ g)\cdot g'. The chain rule may also be expressed in Leibniz's notation. If a variable depends on the variable , which itself depends on the variable (that is, and are dependent variables), then depends on as well, via the intermediate variable . In this case, the chain rule is expressed as \frac = \frac \cdot \frac, and \left.\frac\_ = \left.\frac\_ \cdot \left. \frac\_ , for indicating at which points the derivatives have to be evaluated. In integral, integration, the counterpart to the chain rule is the substitution rule. Intuitive explanation Intuitively, the chain rule states that knowing t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cartesian Coordinate System
In geometry, a Cartesian coordinate system (, ) in a plane (geometry), plane is a coordinate system that specifies each point (geometry), point uniquely by a pair of real numbers called ''coordinates'', which are the positive and negative numbers, signed distances to the point from two fixed perpendicular oriented lines, called ''coordinate lines'', ''coordinate axes'' or just ''axes'' (plural of ''axis'') of the system. The point where the axes meet is called the ''Origin (mathematics), origin'' and has as coordinates. The axes direction (geometry), directions represent an orthogonal basis. The combination of origin and basis forms a coordinate frame called the Cartesian frame. Similarly, the position of any point in three-dimensional space can be specified by three ''Cartesian coordinates'', which are the signed distances from the point to three mutually perpendicular planes. More generally, Cartesian coordinates specify the point in an -dimensional Euclidean space for any di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jacobian Matrix
In vector calculus, the Jacobian matrix (, ) of a vector-valued function of several variables is the matrix of all its first-order partial derivatives. If this matrix is square, that is, if the number of variables equals the number of components of function values, then its determinant is called the Jacobian determinant. Both the matrix and (if applicable) the determinant are often referred to simply as the Jacobian. They are named after Carl Gustav Jacob Jacobi. The Jacobian matrix is the natural generalization to vector valued functions of several variables of the derivative and the differential of a usual function. This generalization includes generalizations of the inverse function theorem and the implicit function theorem, where the non-nullity of the derivative is replaced by the non-nullity of the Jacobian determinant, and the multiplicative inverse of the derivative is replaced by the inverse of the Jacobian matrix. The Jacobian determinant is fundamentally used f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gradient
In vector calculus, the gradient of a scalar-valued differentiable function f of several variables is the vector field (or vector-valued function) \nabla f whose value at a point p gives the direction and the rate of fastest increase. The gradient transforms like a vector under change of basis of the space of variables of f. If the gradient of a function is non-zero at a point p, the direction of the gradient is the direction in which the function increases most quickly from p, and the magnitude of the gradient is the rate of increase in that direction, the greatest absolute directional derivative. Further, a point where the gradient is the zero vector is known as a stationary point. The gradient thus plays a fundamental role in optimization theory, where it is used to minimize a function by gradient descent. In coordinate-free terms, the gradient of a function f(\mathbf) may be defined by: df=\nabla f \cdot d\mathbf where df is the total infinitesimal change in f for a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vector Field
In vector calculus and physics, a vector field is an assignment of a vector to each point in a space, most commonly Euclidean space \mathbb^n. A vector field on a plane can be visualized as a collection of arrows with given magnitudes and directions, each attached to a point on the plane. Vector fields are often used to model, for example, the speed and direction of a moving fluid throughout three dimensional space, such as the wind, or the strength and direction of some force, such as the magnetic or gravitational force, as it changes from one point to another point. The elements of differential and integral calculus extend naturally to vector fields. When a vector field represents force, the line integral of a vector field represents the work done by a force moving along a path, and under this interpretation conservation of energy is exhibited as a special case of the fundamental theorem of calculus. Vector fields can usefully be thought of as representing the velocit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |