|
Kushner Equation
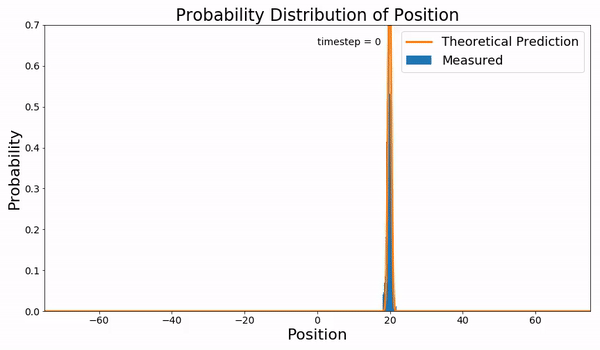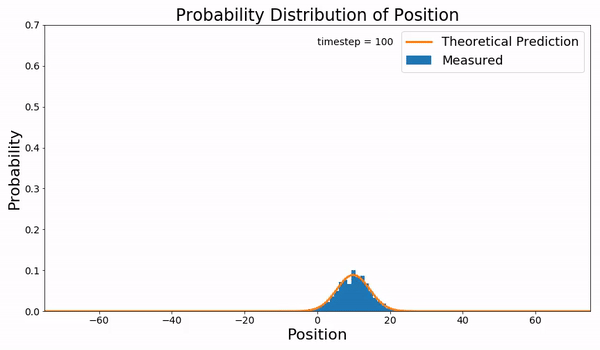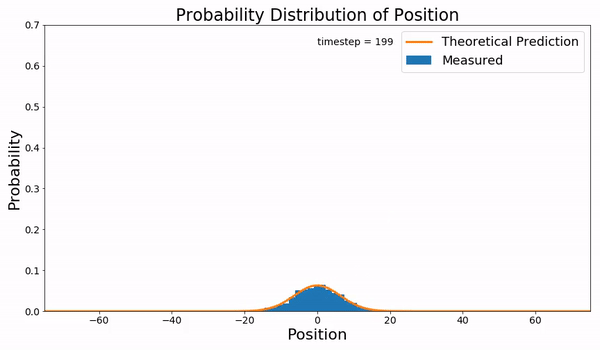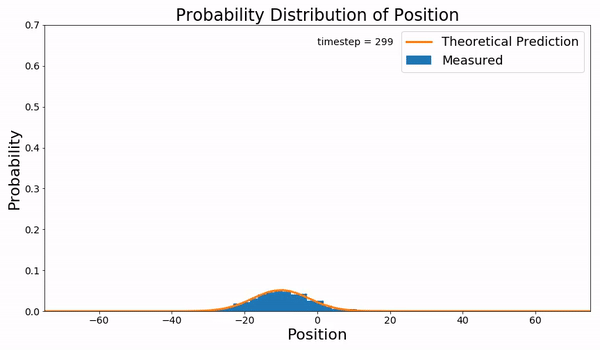
In filtering theory the Kushner equation (after Harold Kushner) is an equation for the conditional probability density of the state of a stochastic non-linear dynamical system, given noisy measurements of the state. It therefore provides the solution of the nonlinear filtering problem in estimation theory. The equation is sometimes referred to as the Stratonovich–Kushner Stratonovich, R.L. (1960). ''Conditional Markov Processes''. Theory of Probability and Its Applications, 5, pp. 156–178. (or Kushner–Stratonovich) equation. Overview Assume the state of the system evolves according to :dx = f(x,t) \, dt + \sigma\, dw and a noisy measurement of the system state is available: :dz = h(x,t) \, dt + \eta\, dv where ''w'', ''v'' are independent Wiener processes. Then the conditional probability density ''p''(''x'', ''t'') of the state at time ''t'' is given by the Kushner equation: :dp(x,t) = L (x,t)dt + p(x,t) \big(h(x,t)-E_t h(x,t) \big)^\top \eta^\eta^ \b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Filtering Problem (stochastic Processes)
In the theory of stochastic processes, filtering describes the problem of determining the state of a system from an incomplete and potentially noisy set of observations. For example, in GPS navigation, filtering helps estimate a car’s true position (the state) from noisy satellite signals (the observations). While originally motivated by problems in engineering, filtering found applications in many fields from signal processing to finance. The problem of optimal non-linear filtering (even for the non-stationary case) was solved by Ruslan L. Stratonovich (1959, 1960), see also Harold J. Kushner's work and Moshe Zakai's, who introduced a simplified dynamics for the unnormalized conditional law of the filter known as the Zakai equation. The solution, however, is infinite-dimensional in the general case.Mireille Chaleyat-Maurel and Dominique Michel. Des resultats de non existence de filtre de dimension finie. Stochastics, 13(1+2):83-102, 1984. Certain approximations and special ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zakai Equation
In filtering theory the Zakai equation is a linear stochastic partial differential equation for the un-normalized density of a hidden state. In contrast, the Kushner equation gives a non-linear stochastic partial differential equation for the normalized density of the hidden state. In principle either approach allows one to estimate a quantity function (the state of a dynamical system) from noisy measurements, even when the system is non-linear (thus generalizing the earlier results of Wiener and Kalman for linear systems and solving a central problem in estimation theory). The application of this approach to a specific engineering situation may be problematic however, as these equations are quite complex. The Zakai equation is a bilinear stochastic partial differential equation. It was named after Moshe Zakai. __NOTOC__ Overview Assume the state of the system evolves according to :dx = f(x,t) dt + dw and a noisy measurement of the system state is available: :dz = h(x,t) d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kalman–Bucy Filter
In statistics and control theory, Kalman filtering (also known as linear quadratic estimation) is an algorithm that uses a series of measurements observed over time, including statistical noise and other inaccuracies, to produce estimates of unknown variables that tend to be more accurate than those based on a single measurement, by estimating a joint probability distribution over the variables for each time-step. The filter is constructed as a mean squared error minimiser, but an alternative derivation of the filter is also provided showing how the filter relates to maximum likelihood statistics. The filter is named after Rudolf E. Kálmán. Kalman filtering has numerous technological applications. A common application is for guidance, navigation, and control of vehicles, particularly aircraft, spacecraft and ships positioned dynamically. Furthermore, Kalman filtering is much applied in time series analysis tasks such as signal processing and econometrics. Kalman filtering is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Innovation (signal Processing)
In time series analysis (or forecasting) — as conducted in statistics, signal processing, and many other fields — the innovation is the difference between the observed value of a variable at time ''t'' and the optimal forecast of that value based on information available prior to time ''t''. If the forecasting method is working correctly, successive innovations are uncorrelated with each other, i.e., constitute a white noise time series. Thus it can be said that the innovation time series is obtained from the measurement time series by a process of 'whitening', or removing the predictable component. The use of the term innovation in the sense described here is due to Hendrik Bode and Claude Shannon (1950) in their discussion of the Wiener filter problem, although the notion was already implicit in the work of Kolmogorov.Mitter, S. K. (1982). Nonlinear filtering of diffusion processes a guided tour. In ''Advances in Filtering and Optimal Stochastic Control'' (pp. 256-266). Sprin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fokker–Planck Equation
In statistical mechanics and information theory, the Fokker–Planck equation is a partial differential equation that describes the time evolution of the probability density function of the velocity of a particle under the influence of drag (physics), drag forces and random forces, as in Brownian motion. The equation can be generalized to other observables as well. The Fokker–Planck equation has multiple applications in information theory, graph theory, data science, finance, economics etc. It is named after Adriaan Fokker and Max Planck, who described it in 1914 and 1917. It is also known as the Kolmogorov forward equation, after Andrey Kolmogorov, who independently discovered it in 1931. When applied to particle position distributions, it is better known as the Smoluchowski equation (after Marian Smoluchowski), and in this context it is equivalent to the convection–diffusion equation. When applied to particle position and momentum distributions, it is known as the Klein–Kr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wiener Process
In mathematics, the Wiener process (or Brownian motion, due to its historical connection with Brownian motion, the physical process of the same name) is a real-valued continuous-time stochastic process discovered by Norbert Wiener. It is one of the best known Lévy processes (càdlàg stochastic processes with stationary increments, stationary independent increments). It occurs frequently in pure and applied mathematics, economy, economics, quantitative finance, evolutionary biology, and physics. The Wiener process plays an important role in both pure and applied mathematics. In pure mathematics, the Wiener process gave rise to the study of continuous time martingale (probability theory), martingales. It is a key process in terms of which more complicated stochastic processes can be described. As such, it plays a vital role in stochastic calculus, diffusion processes and even potential theory. It is the driving process of Schramm–Loewner evolution. In applied mathematics, the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ruslan Stratonovich
Ruslan Leont'evich Stratonovich () was a Russian physicist, engineer, and probabilist and one of the founders of the theory of stochastic differential equations. Biography Ruslan Stratonovich was born on 31 May 1930 in Moscow. He studied from 1947 at the Moscow State University, specializing in there under P. I. Kuznetsov on radio physics (a Soviet term for oscillation physics – including noise – in the broadest sense, but especially in the electromagnetic spectrum). In 1953 he graduated and came into contact with the mathematician Andrey Kolmogorov. In 1956 he received his doctorate on the application of the theory of correlated random points to the calculation of electronic noise. In 1969 he became professor of physics at the Moscow State University. Research Stratonovich invented a stochastic calculus which serves as an alternative to the Itō calculus; the Stratonovich calculus is most natural when physical laws are being considered. The Stratonovich integral appears ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ruslan L
Ruslan may refer to: * ''Ruslan'' (film), a 2009 film starring Steven Segal * '' Ruslaan'', a 2024 Indian film * Ruslan (given name), masculine given name (contains list of people) * Antonov An-124 ''Ruslan'', large Soviet cargo aircraft, later built in Ukraine and Russia * SS ''Ruslan'', a Russian cargo ship in the Third Aliyah in 1919 See also * Aslan (other) Aslan is the fictional lion in C. S. Lewis's ''Chronicles of Narnia''. Aslan or ''Arslan'' (both spellings of a Turkic word meaning "fearless", "warrior", "lion") may also refer to: People Given name Arsalan * Arsalan Anwar (born 1986), P ..., cognate * Rusian (other) * Ruslan and Ludmila (other) {{disambig ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Harold J
Harold may refer to: People * Harold (given name), including a list of persons and fictional characters with the name * Harold (surname), surname in the English language * András Arató, known in meme culture as "Hide the Pain Harold" Arts and entertainment * ''Harold'' (film), a 2008 comedy film * ''Harold'', an 1876 poem by Alfred, Lord Tennyson * ''Harold, the Last of the Saxons'', an 1848 book by Edward Bulwer-Lytton, 1st Baron Lytton * '' Harold or the Norman Conquest'', an opera by Frederic Cowen * ''Harold'', an 1885 opera by Eduard Nápravník * Harold, a character from the cartoon ''The Grim Adventures of Billy & Mandy'' * Harold & Kumar, a US movie; Harold/Harry is the main actor in the show. Places ;In the United States * Alpine, Los Angeles County, California, an erstwhile settlement that was also known as Harold * Harold, Florida, an unincorporated community * Harold, Kentucky, an unincorporated community * Harold, Missouri, an unincorporated commun ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Estimation Theory
Estimation theory is a branch of statistics that deals with estimating the values of Statistical parameter, parameters based on measured empirical data that has a random component. The parameters describe an underlying physical setting in such a way that their value affects the distribution of the measured data. An ''estimator'' attempts to approximate the unknown parameters using the measurements. In estimation theory, two approaches are generally considered: * The probabilistic approach (described in this article) assumes that the measured data is random with probability distribution dependent on the parameters of interest * The set estimation, set-membership approach assumes that the measured data vector belongs to a set which depends on the parameter vector. Examples For example, it is desired to estimate the proportion of a population of voters who will vote for a particular candidate. That proportion is the parameter sought; the estimate is based on a small random sa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nonlinear Filter
In signal processing, a nonlinear filter is a filter whose output is not a linear function of its input. That is, if the filter outputs signals and for two input signals and separately, but does not always output when the input is a linear combination . Both continuous-domain and discrete-domain filters may be nonlinear. A simple example of the former would be an electrical device whose output voltage at any moment is the square of the input voltage ; or which is the input clipped to a fixed range , namely . An important example of the latter is the running-median filter, such that every output sample is the median of the last three input samples . Like linear filters, nonlinear filters may be shift invariant or not. Non-linear filters have many applications, especially in the removal of certain types of noise that are not additive. For example, the median filter is widely used to remove spike noise — that affects only a small percentage of the samples, possibly b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |