Fokker–Planck equation

In statistical mechanics and information theory, the Fokker–Planck equation is a partial differential equation that describes the time evolution of the probability density function of the velocity of a particle under the influence of drag forces and random forces, as in Brownian motion. The equation can be generalized to other observables as well. The Fokker–Planck equation has multiple applications in information theory, graph theory, data science, finance, economics etc.

It is named after Adriaan Fokker and Max Planck, who described it in 1914 and 1917. It is also known as the Kolmogorov forward equation, after Andrey Kolmogorov, who independently discovered it in 1931. When applied to particle position distributions, it is better known as the Smoluchowski equation (after Marian Smoluchowski), and in this context it is equivalent to the convection–diffusion equation. When applied to particle position and momentum distributions, it is known as the Klein–Kramers equation. The case with zero diffusion is the continuity equation. The Fokker–Planck equation is obtained from the master equation through Kramers–Moyal expansion.

The first consistent microscopic derivation of the Fokker–Planck equation in the single scheme of classical and quantum mechanics was performed by Nikolay Bogoliubov and Nikolay Krylov.

One dimension

In one spatial dimension ''x'', for an Itô process driven by the standard Wiener process $W_t$ and described by the stochastic differential equation (SDE)
$dX_t = \mu(X_t, t) \,dt + \sigma(X_t, t) \,dW_t$
with drift $\mu(X_t, t)$ and diffusion coefficient $D(X_t, t) = \sigma^2(X_t, t)/2$, the Fokker–Planck equation for the probability density $p(x, t)$ of the random variable $X_t$ is
In the following, use $\sigma = \sqrt$.

Define the infinitesimal generator $\mathcal$ (the following can be found in Ref.):

\mathcalp(X_t) = \lim_ \frac1\left(\mathbb\big (X_) \mid X_t = x \big- p(x)\right).

The ''transition probability'' $\mathbb_(x \mid x')$, the probability of going from $(t', x')$ to $(t, x)$, is introduced here; the expectation can be written as
$\mathbb(p(X_) \mid X_t = x) = \int p(y) \, \mathbb_(y \mid x) \,dy.$
Now we replace in the definition of $\mathcal$, multiply by $\mathbb_(x \mid x')$ and integrate over $dx$. The limit is taken on
$\int p(y) \int \mathbb_(y \mid x)\,\mathbb_(x \mid x') \,dx \,dy - \int p(x) \, \mathbb_(x \mid x') \,dx.$
Note now that
$\int \mathbb_(y \mid x) \, \mathbb_(x \mid x') \,dx = \mathbb_(y \mid x'),$
which is the Chapman–Kolmogorov theorem. Changing the dummy variable $y$ to $x$, one gets
$\begin \int p(x) \lim_ \frac1 \left( \mathbb_(x \mid x') - \mathbb_(x \mid x') \right) \,dx, \end$
which is a time derivative. Finally we arrive to

\int mathcalp(x)\mathbb_(x \mid x') \,dx = \int p(x) \, \partial_t \mathbb_(x \mid x') \,dx.

From here, the Kolmogorov backward equation can be deduced. If we instead use the adjoint operator of $\mathcal$, $\mathcal^\dagger$, defined such that

\int mathcalp(x)\mathbb_(x \mid x') \,dx = \int p(x) mathcal^\dagger \mathbb_(x \mid x')\,dx,

then we arrive to the Kolmogorov forward equation, or Fokker–Planck equation, which, simplifying the notation $p(x, t) = \mathbb_(x \mid x')$, in its differential form reads
$\mathcal^\dagger p(x, t) = \partial_t p(x, t).$

Remains the issue of defining explicitly $\mathcal$. This can be done taking the expectation from the integral form of the Itô's lemma:
$\mathbb\big(p(X_t)\big) = p(X_0) + \mathbb\left(\int_0^t \left(\partial_t + \mu\partial_x + \frac\partial_x^2 \right) p(X_) \,dt'\right).$

The part that depends on $dW_t$ vanished because of the martingale property.

Then, for a particle subject to an Itô equation, using
$\mathcal = \mu\partial_x + \frac\partial_x^2,$
it can be easily calculated, using integration by parts, that
$\mathcal^\dagger = -\partial_x(\mu \cdot) + \frac12 \partial_x^2(\sigma^2 \cdot),$
which bring us to the Fokker–Planck equation:
$\partial_t p(x, t) = -\partial_x \big(\mu(x, t) \cdot p(x, t)\big) + \partial_x^2\left(\frac \, p(x,t)\right).$

While the Fokker–Planck equation is used with problems where the initial distribution is known, if the problem is to know the distribution at previous times, the Feynman–Kac formula can be used, which is a consequence of the Kolmogorov backward equation.

The stochastic process defined above in the Itô sense can be rewritten within the Stratonovich convention as a Stratonovich SDE:
dX_t = \left mu(X_t, t) - \frac \fracD(X_t, t)\right\,dt + \sqrt \circ dW_t.
It includes an added noise-induced drift term due to diffusion gradient effects if the noise is state-dependent. This convention is more often used in physical applications. Indeed, it is well known that any solution to the Stratonovich SDE is a solution to the Itô SDE.

The zero-drift equation with constant diffusion can be considered as a model of classical Brownian motion:
\frac p(x, t) = D_0\frac\left (x, t)\right

This model has discrete spectrum of solutions if the condition of fixed boundaries is added for $\$:
$\begin p(0, t) &= p(L, t) = 0, \\ p(x, 0) &= p_0(x). \end$

It has been shown that in this case an analytical spectrum of solutions allows deriving a local uncertainty relation for the coordinate-velocity phase volume:
$\Delta x \, \Delta v \geq D_0.$
Here $D_0$ is a minimal value of a corresponding diffusion spectrum $D_j$, while $\Delta x$ and $\Delta v$ represent the uncertainty of coordinate–velocity definition.

Higher dimensions

More generally, if

$d\mathbf_t = \boldsymbol(\mathbf_t,t)\,dt + \boldsymbol(\mathbf_t,t)\,d\mathbf_t,$

where $\mathbf_t$ and $\boldsymbol(\mathbf_t,t)$ are -dimensional vectors, $\boldsymbol(\mathbf_t,t)$ is an $N \times M$ matrix and $\mathbf_t$ is an ''M''-dimensional standard Wiener process, the probability density $p(\mathbf,t)$ for $\mathbf_t$ satisfies the Fokker–Planck equationwith drift vector $\boldsymbol = (\mu_1,\ldots,\mu_N)$ and diffusion tensor $\mathbf = \frac \boldsymbol^\mathsf$, i.e.$D_(\mathbf,t) = \frac\sum_^M \sigma_(\mathbf,t) \sigma_(\mathbf,t).$

If instead of an Itô SDE, a Stratonovich SDE is considered,

$d\mathbf_t = \boldsymbol(\mathbf_t,t)\,dt + \boldsymbol(\mathbf_t,t)\circ d\mathbf_t,$

the Fokker–Planck equation will read:

\frac = -\sum_^N \frac \left \mu_i(\mathbf,t) \, p(\mathbf,t) \right+ \frac \sum_^M \sum_^ \frac \left\

Generalization

In general, the Fokker–Planck equations are a special case to the general Kolmogorov forward equation

$\partial_t \rho = \mathcal^*\rho$

where the linear operator $\mathcal^*$ is the Hermitian adjoint to the infinitesimal generator for the Markov process.

Examples

Wiener process

A standard scalar Wiener process is generated by the stochastic differential equation

$dX_t = dW_t.$

Here the drift term is zero and the diffusion coefficient is 1/2. Thus the corresponding Fokker–Planck equation is

$\frac = \frac \frac,$

which is the simplest form of a diffusion equation. If the initial condition is $p(x,0) = \delta(x)$, the solution is

$p(x,t) = \frace^.$

Boltzmann distribution at the thermodynamic equilibrium

The overdamped Langevin equation$dx_t = -\frac (\nabla_x U)dt + dW_t$gives $\partial_t p = \frac 1 2 \nabla\cdot \left(\frac \nabla U + \nabla p\right)$. The Boltzmann distribution $p(x) \propto e^$ is an equilibrium distribution, and assuming $U$ grows sufficiently rapidly (that is, the potential well is deep enough to confine the particle), the Boltzmann distribution is the unique equilibrium.

Ornstein–Uhlenbeck process

The Ornstein–Uhlenbeck process is a process defined as

$dX_t = -a X_t \, dt + \sigma \, dW_t.$

with $a>0$. Physically, this equation can be motivated as follows: a particle of mass $m$ with velocity $V_t$ moving in a medium, e.g., a fluid, will experience a friction force which resists motion whose magnitude can be approximated as being proportional to particle's velocity $-a V_t$ with $a = \mathrm$. Other particles in the medium will randomly kick the particle as they collide with it and this effect can be approximated by a white noise term; $\sigma (d W_t/dt)$. Newton's second law is written as

$m \frac=-a V_t +\sigma \frac.$

Taking $m = 1$ for simplicity and changing the notation as $V_t\rightarrow X_t$ leads to the familiar form $dX_t = -a X_t dt + \sigma dW_t$.

The corresponding Fokker–Planck equation is
$\frac = a \frac\left(x \,p(x,t)\right) + \frac \frac,$

The stationary solution ($\partial_t p = 0$) is
$p_(x) = \sqrt e^.$

Plasma physics

In plasma physics, the distribution function for a particle species $s$, $p_s (\mathbf,\mathbf,t)$, takes the place of the probability density function. The corresponding Boltzmann equation is given by

$\frac + \mathbf \cdot \boldsymbol p_s + \frac \left( \mathbf + \mathbf \times \mathbf \right) \cdot \boldsymbol_v p_s = -\frac \left(p_s \langle\Delta v_i\rangle\right) + \frac \frac \left(p_s \langle\Delta v_i \, \Delta v_j\rangle\right),$

where the third term includes the particle acceleration due to the Lorentz force and the Fokker–Planck term at the right-hand side represents the effects of particle collisions. The quantities $\langle\Delta v_i\rangle$ and $\langle\Delta v_i \, \Delta v_j\rangle$ are the average change in velocity a particle of type $s$ experiences due to collisions with all other particle species in unit time. Expressions for these quantities are given elsewhere. If collisions are ignored, the Boltzmann equation reduces to the Vlasov equation.

Smoluchowski diffusion equation

Consider an overdamped Brownian particle under external force $F(r)$:$m\ddot = - \gamma \dot + F(r) + \sigma \xi(t)$where the $m\ddot r$ term is negligible (the meaning of "overdamped"). Thus, it is just $\gamma \, dr = F(r)\, dt + \sigma \, dW_t$. The Fokker–Planck equation for this particle is the Smoluchowski diffusion equation:
\partial_t P(r,t, r_0, t_0) = \nabla \cdot r_0, t_0)Where $D$ is the diffusion constant and $\beta = \frac$. The importance of this equation is it allows for both the inclusion of the effect of temperature on the system of particles and a spatially dependent diffusion constant.

Starting with the Langevin Equation of a Brownian particle in external field $F(r)$, where $\gamma$ is the friction term, $\xi$ is a fluctuating force on the particle, and $\sigma$ is the amplitude of the fluctuation.

$m\ddot = - \gamma \dot + F(r) + \sigma \xi(t)$

At equilibrium the frictional force is much greater than the inertial force, $\left\vert \gamma \dot \right\vert \gg \left\vert m \ddot \right\vert$. Therefore, the Langevin equation becomes,

$\gamma \dot = F(r) + \sigma \xi(t)$

Which generates the following Fokker–Planck equation,

$\partial_t P(r,t, r_0,t_0) = \left(\nabla^2\frac - \nabla \cdot \frac\right) P(r,t, r_0,t_0)$

Rearranging the Fokker–Planck equation,

$\partial_t P(r,t, r_0,t_0)= \nabla \cdot \left( \nabla D- \frac\right) P(r,t, r_0,t_0)$

Where $D = \frac$. Note, the diffusion coefficient may not necessarily be spatially independent if $\sigma$ or $\gamma$ are spatially dependent.

Next, the total number of particles in any particular volume is given by,

$N_V (t, r_0, t_0) = \int_V dr P(r,t, r_0,t_0)$

Therefore, the flux of particles can be determined by taking the time derivative of the number of particles in a given volume, plugging in the Fokker–Planck equation, and then applying Gauss's Theorem.

$\partial_t N_V (t, r_0, t_0) = \int_V dV \nabla \cdot\left( \nabla D- \frac\right) P(r,t, r_0, t_0) = \int_ d\mathbf \cdot j(r,t, r_0, t_0)$

$j(r,t, r_0, t_0) = \left( \nabla D- \frac\right)P(r,t, r_0, t_0)$

In equilibrium, it is assumed that the flux goes to zero. Therefore, Boltzmann statistics can be applied for the probability of a particles location at equilibrium, where $F(r) = -\nabla U(r)$ is a conservative force and the probability of a particle being in a state $r$ is given as $P(r,t, r_0, t_0) = \frac$.

$j(r,t, r_0, t_0) = \left( \nabla D- \frac\right)\frac = 0$

$\Rightarrow \nabla D = F(r) \left(\frac - D \beta\right)$

This relation is a realization of the fluctuation–dissipation theorem. Now applying $\nabla \cdot \nabla$ to $D P(r,t, r_0, t_0)$ and using the Fluctuation-dissipation theorem,

$\begin \nabla \cdot \nabla D P(r,t, r_0,t_0) &= \nabla \cdot D \nabla P(r,t, r_0,t_0)+ \nabla \cdot P(r,t, r_0,t_0) \nabla D \\ &=\nabla \cdot D \nabla P(r,t, r_0,t_0)+\nabla \cdot P(r,t, r_0,t_0) \frac - \nabla \cdot P(r,t, r_0,t_0) D \beta F(r) \end$

Rearranging,

$\Rightarrow \nabla \cdot \left( \nabla D- \frac\right)P(r,t, r_0,t_0)= \nabla \cdot D(\nabla-\beta F(r)) P(r,t, r_0,t_0)$

Therefore, the Fokker–Planck equation becomes the Smoluchowski equation,
$\partial_t P(r,t, r_0, t_0) = \nabla \cdot D (\nabla - \beta F(r)) P(r,t, r_0, t_0)$
for an arbitrary force $F(r)$.

Computational considerations

Brownian motion follows the Langevin equation, which can be solved for many different stochastic forcings with results being averaged (canonical ensemble in molecular dynamics). However, instead of this computationally intensive approach, one can use the Fokker–Planck equation and consider the probability $p(\mathbf, t)\,d\mathbf$ of the particle having a velocity in the interval $(\mathbf, \mathbf + d\mathbf)$ when it starts its motion with $\mathbf_0$ at time 0.

1-D linear potential example

Brownian dynamics in one dimension is simple.

Theory

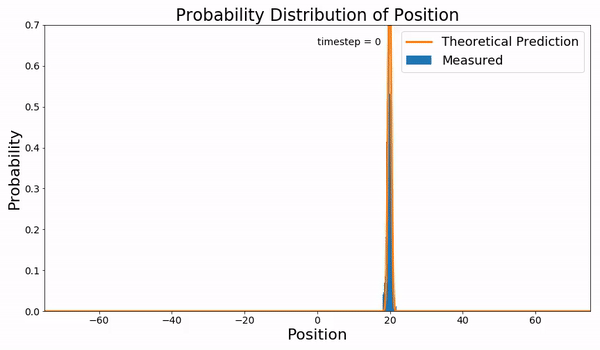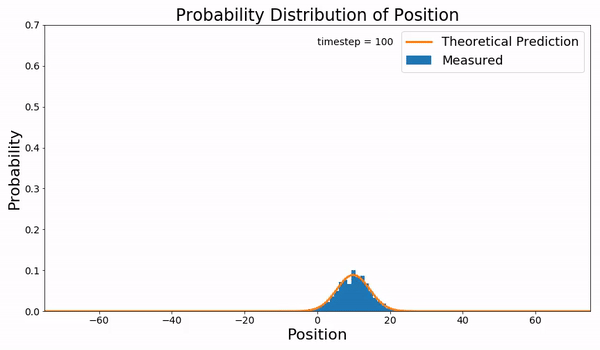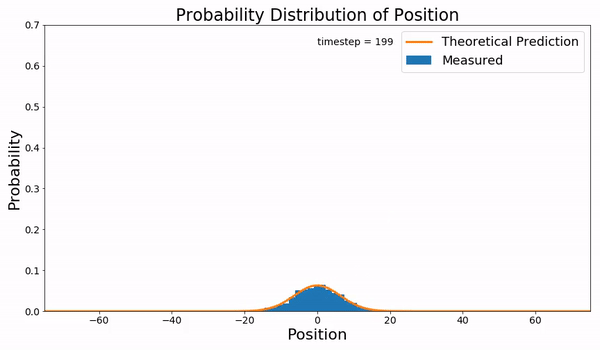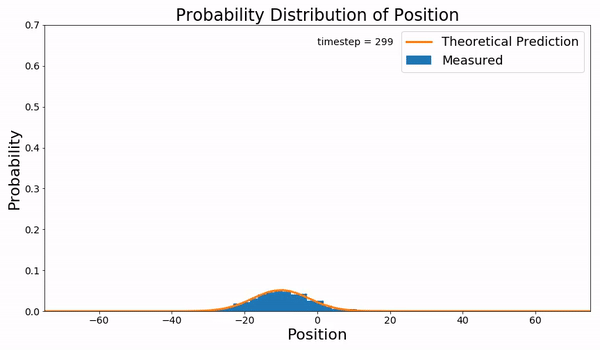
Starting with a linear potential of the form $U(x) = cx$ the corresponding Smoluchowski equation becomes,

$\partial_t P(x,t, x_0, t_0) = \partial_x D (\partial_x + \beta c) P(x,t, x_0, t_0)$

Where the diffusion constant, $D$, is constant over space and time. The boundary conditions are such that the probability vanishes at $x \rightarrow \pm \infin$ with an initial condition of the ensemble of particles starting in the same place, $P(x,t=t_0, x_0,t_0)= \delta (x-x_0)$.

Defining $\tau = D t$ and $b = \beta c$ and applying the coordinate transformation,

$y = x +\tau b ,\ \ \ y_0= x_0 + \tau_0 b$

With $P(x, t, , x_0, t_0) = q(y, \tau, y_0, \tau_0)$ the Smoluchowki equation becomes,
$\partial_\tau q(y, \tau, y_0, \tau_0) =\partial_y^2 q(y, \tau, y_0, \tau_0)$

Which is the free diffusion equation with solution,
$q(y, \tau, y_0, \tau_0)= \frac e^$

And after transforming back to the original coordinates,
$P(x, t , x_0, t_0)= \frac \exp$

Simulation

The simulation on the right was completed using a Brownian dynamics simulation. Starting with a Langevin equation for the system,
$m\ddot = - \gamma \dot -c + \sigma \xi(t)$
where $\gamma$ is the friction term, $\xi$ is a fluctuating force on the particle, and $\sigma$ is the amplitude of the fluctuation. At equilibrium the frictional force is much greater than the inertial force, $\left, \gamma \dot \ \gg \left, m \ddot \$. Therefore, the Langevin equation becomes,
$\gamma \dot = -c + \sigma \xi(t)$

For the Brownian dynamic simulation the fluctuation force $\xi(t)$ is assumed to be Gaussian with the amplitude being dependent of the temperature of the system $\sigma = \sqrt$. Rewriting the Langevin equation,

$\frac=-D \beta c + \sqrt\xi(t)$
where $D = \frac$ is the Einstein relation. The integration of this equation was done using the Euler–Maruyama method to numerically approximate the path of this Brownian particle.

Solution

Being a partial differential equation, the Fokker–Planck equation can be solved analytically only in special cases. A formal analogy of the Fokker–Planck equation with the Schrödinger equation allows the use of advanced operator techniques known from quantum mechanics for its solution in a number of cases. Furthermore, in the case of overdamped dynamics when the Fokker–Planck equation contains second partial derivatives with respect to all spatial variables, the equation can be written in the form of a master equation that can easily be solved numerically.
In many applications, one is only interested in the steady-state probability distribution $p_0(x)$, which can be found from $\frac = 0$.
The computation of mean first passage times and splitting probabilities can be reduced to the solution of an ordinary differential equation which is intimately related to the Fokker–Planck equation.

Particular cases with known solution and inversion

In mathematical finance for volatility smile modeling of options via local volatility, one has the problem of deriving a diffusion coefficient $(\mathbf_t,t)$ consistent with a probability density obtained from market option quotes. The problem is therefore an inversion of the Fokker–Planck equation: Given the density f(x,t) of the option underlying ''X'' deduced from the option market, one aims at finding the local volatility $(\mathbf_t,t)$ consistent with ''f''. This is an inverse problem that has been solved in general by Dupire (1994, 1997) with a non-parametric solution. Brigo and Mercurio (2002, 2003) propose a solution in parametric form via a particular local volatility $(\mathbf_t,t)$ consistent with a solution of the Fokker–Planck equation given by a mixture model. More information is available also in Fengler (2008), Gatheral (2008), and Musiela and Rutkowski (2008).

Fokker–Planck equation and path integral

Every Fokker–Planck equation is equivalent to a path integral. The path integral formulation is an excellent starting point for the application of field theory methods. This is used, for instance, in critical dynamics.

A derivation of the path integral is possible in a similar way as in quantum mechanics. The derivation for a Fokker–Planck equation with one variable $x$ is as follows. Start by inserting a delta function and then integrating by parts:

\begin
\frac p
& = - \frac \left D_1(x',t) p(x',t) \right+ \frac \left D_2(x',t) p(x',t) \right\\ ex& = \int_^ dx\left \left( D_ \frac + D_2 \frac\right) \delta \rightp(x,t).
\end

The $x$-derivatives here only act on the $\delta$-function, not on $p(x,t)$. Integrate over a time interval $\varepsilon$,

p(x', t + \varepsilon) =\int_^\infty \, \mathrmx\left(\left( 1+\varepsilon \left D_1(x,t) \frac \partial + D_2(x,t) \frac\rightright) \delta(x' - x) \right) p(x,t)+O(\varepsilon^2).

Insert the Fourier integral

$\delta = \int_^ \frac e^$

for the $\delta$-function,

\begin
p(x', t+\varepsilon) & = \int_^\infty \mathrmx \int_^ \frac \left(1+\varepsilon \left \tilde D_1(x,t) +\tilde^2 D_2(x,t) \right\right) e^p(x,t) +O(\varepsilon^2) \\ pt& =\int_^\infty \mathrmx \int_^ \frac\exp \left( \varepsilon \left -\tilde\frac\varepsilon + \tilde D_1(x,t) +\tilde^2 D_2(x,t) \right\right) p(x,t) +O(\varepsilon^2).
\end

This equation expresses $p(x', t+\varepsilon)$ as functional of $p(x,t)$. Iterating $(t'-t)/\varepsilon$ times and performing the limit $\varepsilon \rightarrow 0$ gives a path integral with action

S=\int \mathrmt\left \tilde D_1 (x,t) +\tilde^2 D_2 (x,t) -\tilde\frac \right

The variables $\tilde$ conjugate to $x$ are called "response variables".

Although formally equivalent, different problems may be solved more easily in the Fokker–Planck equation or the path integral formulation. The equilibrium distribution for instance may be obtained more directly from the Fokker–Planck equation.

See also

* Bogoliubov–Born–Green–Kirkwood–Yvon hierarchy of equations
* Boltzmann equation
* Convection–diffusion equation
* Klein–Kramers equation
* Kolmogorov backward equation
* Kolmogorov equation
* Langevin equation
* Master equation
* Mean-field game theory
* Ornstein–Uhlenbeck process
* Vlasov equation

Notes and references

Further reading

*
*
*
*

{{DEFAULTSORT:Fokker-Planck equation
Stochastic processes
Equations
Parabolic partial differential equations
Max Planck
Stochastic calculus
Mathematical finance
Transport phenomena