|
Jyā, Koti-jyā And Utkrama-jyā
Jyā, koṭi-jyā and utkrama-jyā are three trigonometric functions introduced by Indian mathematics, Indian mathematicians and astronomers. The earliest known Indian treatise containing references to these functions is Surya Siddhanta. These are functions of arcs of circles and not functions of angles. Jyā and koti-jyā are closely related to the modern trigonometric functions of sine and cosine. In fact, the origins of the modern terms of "sine" and "cosine" have been traced back to the Sanskrit words jyā and koti-jyā. Definition Let 'arc AB' denote an Arc (geometry), arc whose two extremities are A and B of a circle with center 'O'. If a perpendicular BM is dropped from B to OA, then: * ''jyā'' of arc AB = BM * ''koti-jyā'' of arc AB = OM * ''utkrama-jyā'' of arc AB = MA If the radius of the circle is ''R'' and the length of arc AB is ''s'', the angle subtended by arc AB at O measured in radians is θ = ''s'' / ''R''. The three Indian functions are related to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trigonometric Functions
In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all sciences that are related to geometry, such as navigation, solid mechanics, celestial mechanics, geodesy, and many others. They are among the simplest periodic functions, and as such are also widely used for studying periodic phenomena through Fourier analysis. The trigonometric functions most widely used in modern mathematics are the sine, the cosine, and the tangent functions. Their multiplicative inverse, reciprocals are respectively the cosecant, the secant, and the cotangent functions, which are less used. Each of these six trigonometric functions has a corresponding Inverse trigonometric functions, inverse function, and an analog among the hyperbolic functions. The oldest definitions of trigonometric functions, related to right-an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cathetus
In a right triangle, a cathetus (originally from Greek , "perpendicular"; plural: catheti), commonly known as a leg, is either of the sides that are adjacent to the right angle. It is occasionally called a "side about the right angle". The side opposite the right angle is the hypotenuse. In the context of the hypotenuse, the catheti are sometimes referred to simply as "the other two sides". If the catheti of a right triangle have equal lengths, the triangle is isosceles. If they have different lengths, a distinction can be made between the minor (shorter) and major (longer) cathetus. The ratio of the lengths of the catheti defines the trigonometric functions tangent and cotangent of the acute angles in the triangle: the ratio c_1/c_2 is the tangent of the acute angle adjacent to c_2 and is also the cotangent of the acute angle adjacent to c_1. In a right triangle, the length of a cathetus is the geometric mean of the length of the adjacent segment cut by the altitude to the h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trigonometry
Trigonometry () is a branch of mathematics concerned with relationships between angles and side lengths of triangles. In particular, the trigonometric functions relate the angles of a right triangle with ratios of its side lengths. The field emerged in the Hellenistic world during the 3rd century BC from applications of geometry to astronomical studies. The Greeks focused on the calculation of chords, while mathematicians in India created the earliest-known tables of values for trigonometric ratios (also called trigonometric functions) such as sine. Throughout history, trigonometry has been applied in areas such as geodesy, surveying, celestial mechanics, and navigation. Trigonometry is known for its many identities. These trigonometric identities are commonly used for rewriting trigonometrical expressions with the aim to simplify an expression, to find a more useful form of an expression, or to solve an equation. History Sumerian astronomers studied angle me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trigonometric Functions
In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all sciences that are related to geometry, such as navigation, solid mechanics, celestial mechanics, geodesy, and many others. They are among the simplest periodic functions, and as such are also widely used for studying periodic phenomena through Fourier analysis. The trigonometric functions most widely used in modern mathematics are the sine, the cosine, and the tangent functions. Their multiplicative inverse, reciprocals are respectively the cosecant, the secant, and the cotangent functions, which are less used. Each of these six trigonometric functions has a corresponding Inverse trigonometric functions, inverse function, and an analog among the hyperbolic functions. The oldest definitions of trigonometric functions, related to right-an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Robert Of Chester
Robert of Chester (Latin: ''Robertus Castrensis'') was an English Arabist of the 12th century. He translated several historically important books from Arabic to Latin, such as: * ''Book on the Composition of Alchemy'' (): translated in 1144, this was the first book on alchemy to become available in Europe *'' Compendious Book on Calculation by Completion and Balancing'' (): al-Khwārizmī's book about |
Muḥammad Ibn Mūsā Al-Khwārizmī
Muhammad ibn Musa al-Khwarizmi , or simply al-Khwarizmi, was a mathematician active during the Islamic Golden Age, who produced Arabic-language works in mathematics, astronomy, and geography. Around 820, he worked at the House of Wisdom in Baghdad, the contemporary capital city of the Abbasid Caliphate. One of the most prominent scholars of the period, his works were widely influential on later authors, both in the Islamic world and Europe. His popularizing treatise on algebra, compiled between 813 and 833 as '' Al-Jabr'' (''The Compendious Book on Calculation by Completion and Balancing''),Oaks, J. (2009), "Polynomials and Equations in Arabic Algebra", ''Archive for History of Exact Sciences'', 63(2), 169–203. presented the first systematic solution of linear and quadratic equations. One of his achievements in algebra was his demonstration of how to solve quadratic equations by completing the square, for which he provided geometric justifications. Because al-Khwarizmi was ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gerard Of Cremona
Gerard of Cremona (Latin: ''Gerardus Cremonensis''; c. 1114 – 1187) was an Italians, Italian translator of scientific books from Arabic into Latin. He worked in Toledo, Spain, Toledo, Kingdom of Castile and obtained the Arabic books in the libraries at Toledo. Some of the books had been originally written in Greek and, although well known in Byzantine Constantinople and Greece at the time, were unavailable in Greek or Latin in Western Europe. Gerard of Cremona is the most important translator among the Toledo School of Translators who invigorated Western medieval Europe in the twelfth century by transmitting the Arabs' and ancient Greeks' knowledge in astronomy, medicine and other sciences, by making the knowledge available in Latin. One of Gerard's most famous translations is of Ptolemy's ''Almagest'' from Arabic texts found in Toledo. Confusingly, there appear to have been two translators of Arabic text into Latin known as ''Gerard of Cremona.'' The first was active in the 12t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Al-Battani
Al-Battani (before 858929), archaically Latinized as Albategnius, was a Muslim astronomer, astrologer, geographer and mathematician, who lived and worked for most of his life at Raqqa, now in Syria. He is considered to be the greatest and most famous of the astronomers of the medieval Islamic world. Al-Battānī's writings became instrumental in the development of science and astronomy in the west. His (), is the earliest extant (astronomical table) made in the Ptolemaic tradition that is hardly influenced by Hindu or Sasanian astronomy. Al-Battānī refined and corrected Ptolemy's ''Almagest'', but also included new ideas and astronomical tables of his own. A handwritten Latin version by the Italian astronomer Plato Tiburtinus was produced between 1134 and 1138, through which medieval astronomers became familiar with al-Battānī. In 1537, a Latin translation of the was printed in Nuremberg. An annotated version, also in Latin, published in three separate volumes betwee ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Plato Tiburtinus
Plato Tiburtinus (, "Plato of Tivoli, Italy, Tivoli"; Floruit, fl. 12th century) was a 12th-century Italian people, Italian mathematician, astronomer and translation, translator who lived in Barcelona from 1116 to 1138. He is best known for translating Hebrew language, Hebrew and Arabic language, Arabic documents into Latin language, Latin, and was apparently the first to translate information on the astrolabe (an astronomical instrument) from Arabic. Plato of Tivoli translated the Arab astrologer Albohali's "Book of Birth" into Latin in 1136. He translated Claudius Ptolemy's Tetrabiblos from Arabic to Latin in 1138, the astronomical works of al-Battani, Theodosius' Spherics, Theodosius' ''Spherics'' and the ''Liber Embadorum'' by Abraham bar Hiyya, Abraham bar Chiia.David Eugene Smith, ''History of Mathematics'', (Dover Publications, Inc, 1951), 201. He has worked together with the Jewish mathematician Savasorda (Abraham Bar Ḥiyya Ha-Nasi). His manuscripts were widely circula ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sinus
Sinus may refer to: History * a sac in front of body worn into a toga, in the typical style of wearing it Anatomy * Sinus (anatomy), a sac or cavity in any organ or tissue ** Paranasal sinuses, air cavities in the cranial bones, especially those near the nose, including: *** Maxillary sinus, is the largest of the paranasal sinuses, under the eyes, in the maxillary bones *** Frontal sinus, superior to the eyes, in the frontal bone, which forms the hard part of the forehead *** Ethmoid sinus, formed from several discrete air cells within the ethmoid bone between the eyes and under the nose *** Sphenoidal sinus, in the sphenoid bone at the center of the skull base under the pituitary gland ** Anal sinuses, the furrows which separate the columns in the rectum ** Dural venous sinuses, venous channels found between layers of dura mater in the brain * Sinus (botany), a space or indentation, usually on a leaf Heart * Sinus node, a structure in the superior part of the right atrium * Sinu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Medieval Latin
Medieval Latin was the form of Literary Latin used in Roman Catholic Church, Roman Catholic Western Europe during the Middle Ages. It was also the administrative language in the former Western Roman Empire, Roman Provinces of Mauretania, Numidia (Roman province), Numidia and Africa (Roman province), Africa Proconsularis under the Vandals, the Exarchate of Africa, Byzantines and the Kingdom of Altava, Romano-Berber Kingdoms, until it declined after the Arab conquest of North Africa, Arab Conquest. Medieval Latin in Southern and Central Visigothic Kingdom, Visigothic Hispania, conquered by the Arabs immediately after North Africa, experienced a similar fate, only recovering its importance after the Reconquista by the Northern Christian Kingdoms. In this region it served as the primary written language, though local languages were also written to varying degrees. Latin functioned as the main medium of scholarly exchange, as the liturgical language of the Roman Catholic Church, Churc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
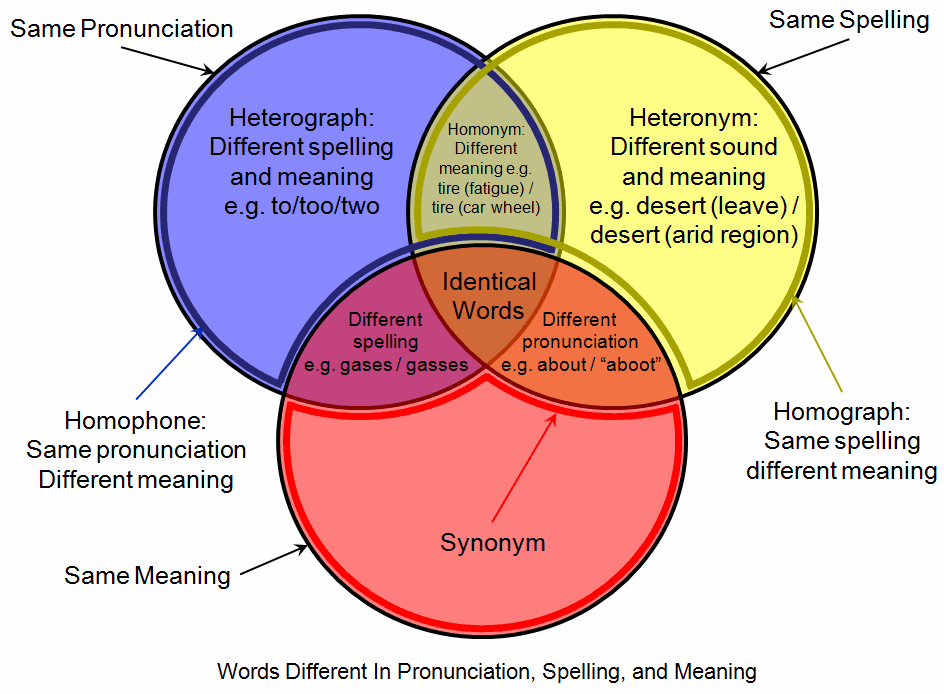
Homograph
A homograph (from the , and , ) is a word that shares the same written form as another word but has a different meaning. However, some dictionaries insist that the words must also be pronounced differently, while the Oxford English Dictionary says that the words should also be of "different origin". In this vein, ''The Oxford Guide to Practical Lexicography'' lists various types of homographs, including those in which the words are discriminated by being in a different ''word class'', such as ''hit'', the verb ''to strike'', and ''hit'', the noun ''a strike''. If, when spoken, the meanings may be distinguished by different pronunciations, the words are also heteronyms. Words with the same writing ''and'' pronunciation (i.e. are both homographs and homophones) are considered homonyms. However, in a broader sense the term "homonym" may be applied to words with the same writing ''or'' pronunciation. Homograph disambiguation is critically important in speech synthesis, natural ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |