|
Integer Quantum Hall Effect
The quantum Hall effect (or integer quantum Hall effect) is a quantized version of the Hall effect which is observed in two-dimensional electron systems subjected to low temperatures and strong magnetic fields, in which the Hall resistance exhibits steps that take on the quantized values : R_ = \frac = \frac , where is the Hall voltage, is the channel current, is the elementary charge and is the Planck constant. The divisor can take on either integer () or fractional () values. Here, is roughly but not exactly equal to the filling factor of Landau levels. The quantum Hall effect is referred to as the integer or fractional quantum Hall effect depending on whether is an integer or fraction, respectively. The striking feature of the integer quantum Hall effect is the persistence of the quantization (i.e. the Hall plateau) as the electron density is varied. Since the electron density remains constant when the Fermi level is in a clean spectral gap, this situation corres ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Mechanics
Quantum mechanics is the fundamental physical Scientific theory, theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is the foundation of all quantum physics, which includes quantum chemistry, quantum field theory, quantum technology, and quantum information science. Quantum mechanics can describe many systems that classical physics cannot. Classical physics can describe many aspects of nature at an ordinary (macroscopic and Microscopic scale, (optical) microscopic) scale, but is not sufficient for describing them at very small submicroscopic (atomic and subatomic) scales. Classical mechanics can be derived from quantum mechanics as an approximation that is valid at ordinary scales. Quantum systems have Bound state, bound states that are Quantization (physics), quantized to Discrete mathematics, discrete values of energy, momentum, angular momentum, and ot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electrical Resistance
The electrical resistance of an object is a measure of its opposition to the flow of electric current. Its reciprocal quantity is , measuring the ease with which an electric current passes. Electrical resistance shares some conceptual parallels with mechanical friction. The SI unit of electrical resistance is the ohm (), while electrical conductance is measured in siemens (S) (formerly called the 'mho' and then represented by ). The resistance of an object depends in large part on the material it is made of. Objects made of electrical insulators like rubber tend to have very high resistance and low conductance, while objects made of electrical conductors like metals tend to have very low resistance and high conductance. This relationship is quantified by resistivity or conductivity. The nature of a material is not the only factor in resistance and conductance, however; it also depends on the size and shape of an object because these properties are extensive rather tha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bell Labs
Nokia Bell Labs, commonly referred to as ''Bell Labs'', is an American industrial research and development company owned by Finnish technology company Nokia. With headquarters located in Murray Hill, New Jersey, Murray Hill, New Jersey, the company operates several laboratories in the United States and around the world. As a former subsidiary of the American Telephone and Telegraph Company (AT&T), Bell Labs and its researchers have been credited with the development of radio astronomy, the transistor, the laser, the photovoltaic cell, the charge-coupled device (CCD), information theory, the Unix operating system, and the programming languages B (programming language), B, C (programming language), C, C++, S (programming language), S, SNOBOL, AWK, AMPL, and others, throughout the 20th century. Eleven Nobel Prizes and five Turing Awards have been awarded for work completed at Bell Laboratories. Bell Labs had its origin in the complex corporate organization of the Bell System telepho ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
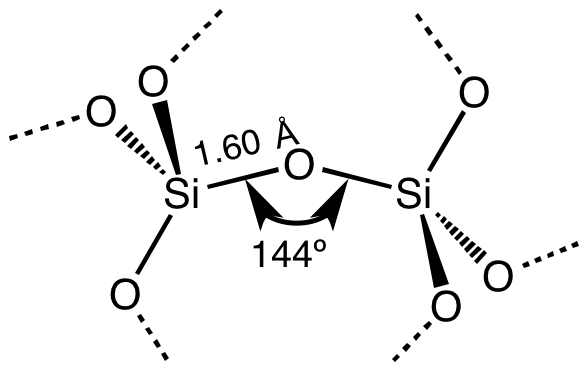
Silicon Dioxide
Silicon dioxide, also known as silica, is an oxide of silicon with the chemical formula , commonly found in nature as quartz. In many parts of the world, silica is the major constituent of sand. Silica is one of the most complex and abundant families of materials, existing as a compound of several minerals and as a synthetic product. Examples include fused quartz, fumed silica, opal, and aerogels. It is used in structural materials, microelectronics, and as components in the food and pharmaceutical industries. All forms are white or colorless, although impure samples can be colored. Silicon dioxide is a common fundamental constituent of glass. Structure In the majority of silicon dioxides, the silicon atom shows tetrahedral coordination, with four oxygen atoms surrounding a central Si atomsee 3-D Unit Cell. Thus, SiO2 forms 3-dimensional network solids in which each silicon atom is covalently bonded in a tetrahedral manner to 4 oxygen atoms. In contrast, CO2 is a li ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Carl Frosch
Carl John Frosch (September 6, 1908 – May 18, 1984) was a Bell Labs researcher. With Lincoln Derrick, Lincoln Derick, Frosch discovered that silicon could be protectively coated by silicon dioxide by the right exposure to oxygen when hot, and patented the method. Such protective coating overcame a problem of surface states found in active silicon circuit elements. The discovery also revealed the potential for the process of silicon Chemical milling, etching. In 1957 Frosch and Derick published their discovery of silicon surface passivation by silicon dioxide, using selective Silicon dioxide, SiO2 predeposition and masking to produce n-type and p-type semiconductor surface patterns. Their transistors were the first in which drain and source were adjacent at the surface, showing that silicon dioxide surface passivation protected and insulated silicon wafers. At Bell Labs, the importance of Frosch's technique was immediately realized. Results of their work circulated around Be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Composite Fermions
A composite fermion is the topological bound state of an electron and an even number of quantized vortices, sometimes visually pictured as the bound state of an electron and, attached, an even number of magnetic flux quanta. Composite fermions were originally envisioned in the context of the fractional quantum Hall effect, but subsequently took on a life of their own, exhibiting many other consequences and phenomena. The concept was first theorized by Jainendra K. Jain in 1989, who co-received the Wolf Prize in Physics in 2025 for this contribution. A further treatment of composite fermions as a Chern–Simons theory was developed by Ana María López and Eduardo Fradkin, and independently by Bertrand Halperin, Nicholas Read, Patrick A. Lee. Vortices are an example of topological defect, and also occur in other situations. Quantized vortices are found in type II superconductors, called Abrikosov vortices. Classical vortices are relevant to the Berezenskii–Kosterlitz–Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chern–Simons Theory
The Chern–Simons theory is a 3-dimensional topological quantum field theory of Schwarz type. It was discovered first by mathematical physicist Albert Schwarz. It is named after mathematicians Shiing-Shen Chern and James Harris Simons, who introduced the Chern–Simons 3-form. In the Chern–Simons theory, the action is proportional to the integral of the Chern–Simons 3-form. In condensed-matter physics, Chern–Simons theory describes composite fermions and the topological order in fractional quantum Hall effect states. In mathematics, it has been used to calculate knot invariants and three-manifold invariants such as the Jones polynomial. Particularly, Chern–Simons theory is specified by a choice of simple Lie group G known as the gauge group of the theory and also a number referred to as the ''level'' of the theory, which is a constant that multiplies the action. The action is gauge dependent, however the partition function of the quantum theory is well-defined whe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Anomaly (physics)
In quantum physics an anomaly or quantum anomaly is the failure of a symmetry of a theory's classical action to be a symmetry of any regularization of the full quantum theory. In classical physics, a classical anomaly is the failure of a symmetry to be restored in the limit in which the symmetry-breaking parameter goes to zero. Perhaps the first known anomaly was the dissipative anomaly in turbulence: time-reversibility remains broken (and energy dissipation rate finite) at the limit of vanishing viscosity Viscosity is a measure of a fluid's rate-dependent drag (physics), resistance to a change in shape or to movement of its neighboring portions relative to one another. For liquids, it corresponds to the informal concept of ''thickness''; for e .... In quantum theory, the first anomaly discovered was the Adler–Bell–Jackiw anomaly, wherein the Chiral_anomaly, axial vector current is conserved as a classical symmetry of electrodynamics, but is broken by the quantized ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gauge Invariance
In physics, a gauge theory is a type of field theory in which the Lagrangian, and hence the dynamics of the system itself, does not change under local transformations according to certain smooth families of operations (Lie groups). Formally, the Lagrangian is invariant under these transformations. The term "gauge" refers to any specific mathematical formalism to regulate redundant degrees of freedom in the Lagrangian of a physical system. The transformations between possible gauges, called gauge transformations, form a Lie group—referred to as the '' symmetry group'' or the gauge group of the theory. Associated with any Lie group is the Lie algebra of group generators. For each group generator there necessarily arises a corresponding field (usually a vector field) called the gauge field. Gauge fields are included in the Lagrangian to ensure its invariance under the local group transformations (called gauge invariance). When such a theory is quantized, the quanta of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
2019 Revision Of The SI
In 2019, four of the seven SI base units specified in the International System of Quantities were redefined in terms of natural physical constants, rather than human artefacts such as the standard kilogram. Effective 20 May 2019, the 144th anniversary of the Metre Convention, the kilogram, ampere, kelvin, and mole are defined by setting exact numerical values, when expressed in SI units, for the Planck constant ('), the elementary electric charge ('), the Boltzmann constant (), and the Avogadro constant (), respectively. The second, metre, and candela had previously been redefined using physical constants. The four new definitions aimed to improve the SI without changing the value of any units, ensuring continuity with existing measurements. In November 2018, the 26th General Conference on Weights and Measures (CGPM) unanimously approved these changes, The conference ran from 13–16 November and the vote on the redefinition was scheduled for the last day. Kazakhstan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conventional Electrical Unit
A conventional electrical unit (or conventional unit where there is no risk of ambiguity) is a unit of measurement in the field of electricity which is based on the so-called "conventional values" of the Josephson constant, the von Klitzing constant agreed by the International Committee for Weights and Measures (CIPM) in 1988, as well as Δ''ν''Cs used to define the second. These units are very similar in scale to their corresponding SI units, but are not identical because of the different values used for the constants. They are distinguished from the corresponding SI units by setting the symbol in italic typeface and adding a subscript "90" – e.g., the conventional volt has the symbol ''V'' – as they came into international use on 1 January 1990. This system was developed to increase the precision of measurements: The Josephson and von Klitzing constants can be realized with great precision, repeatability and ease, and are exactly defined in terms of the universal const ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |