Integer Quantum Hall Effect on:
[Wikipedia]
[Google]
[Amazon]
The quantum Hall effect (or integer quantum Hall effect) is a quantized version of the
 In order to get the number of occupied Landau levels, one defines the so-called filling factor as the ratio between the density of states in a 2DEG and the density of states in the Landau levels.
:
In general the filling factor is not an integer. It happens to be an integer when there is an exact number of filled Landau levels. Instead, it becomes a non-integer when the top level is not fully occupied. In actual experiments, one varies the magnetic field and fixes electron density (and not the Fermi energy!) or varies the electron density and fixes the magnetic field. Both cases correspond to a continuous variation of the filling factor and one cannot expect to be an integer. Since , by increasing the magnetic field, the Landau levels move up in energy and the number of states in each level grow, so fewer electrons occupy the top level until it becomes empty. If the magnetic field keeps increasing, eventually, all electrons will be in the lowest Landau level () and this is called the magnetic quantum limit.
In order to get the number of occupied Landau levels, one defines the so-called filling factor as the ratio between the density of states in a 2DEG and the density of states in the Landau levels.
:
In general the filling factor is not an integer. It happens to be an integer when there is an exact number of filled Landau levels. Instead, it becomes a non-integer when the top level is not fully occupied. In actual experiments, one varies the magnetic field and fixes electron density (and not the Fermi energy!) or varies the electron density and fixes the magnetic field. Both cases correspond to a continuous variation of the filling factor and one cannot expect to be an integer. Since , by increasing the magnetic field, the Landau levels move up in energy and the number of states in each level grow, so fewer electrons occupy the top level until it becomes empty. If the magnetic field keeps increasing, eventually, all electrons will be in the lowest Landau level () and this is called the magnetic quantum limit.

PostscriptPdf
* Magnet Lab Press Releas
* * Zyun F. Ezawa
''Quantum Hall Effects - Field Theoretical Approach and Related Topics.''
World Scientific, Singapore 2008, * Sankar D. Sarma, Aron Pinczuk: ''Perspectives in Quantum Hall Effects.'' Wiley-VCH, Weinheim 2004, * * E. I. Rashba and V. B. Timofeev, Quantum Hall Effect, Sov. Phys. – Semiconductors v. 20, pp. 617–647 (1986). {{Authority control Hall effect Condensed matter physics Quantum electronics Spintronics Quantum phases Mesoscopic physics Articles containing video clips 1980 in science
Hall effect
The Hall effect is the production of a voltage, potential difference (the Hall voltage) across an electrical conductor that is wikt:transverse, transverse to an electric current in the conductor and to an applied magnetic field wikt:perpendicul ...
which is observed in two-dimensional electron systems subjected to low temperature
Temperature is a physical quantity that quantitatively expresses the attribute of hotness or coldness. Temperature is measurement, measured with a thermometer. It reflects the average kinetic energy of the vibrating and colliding atoms making ...
s and strong magnetic field
A magnetic field (sometimes called B-field) is a physical field that describes the magnetic influence on moving electric charges, electric currents, and magnetic materials. A moving charge in a magnetic field experiences a force perpendicular ...
s, in which the Hall resistance exhibits steps that take on the quantized values
:
where is the Hall voltage, is the channel current, is the elementary charge
The elementary charge, usually denoted by , is a fundamental physical constant, defined as the electric charge carried by a single proton (+1 ''e'') or, equivalently, the magnitude of the negative electric charge carried by a single electron, ...
and is the Planck constant
The Planck constant, or Planck's constant, denoted by h, is a fundamental physical constant of foundational importance in quantum mechanics: a photon's energy is equal to its frequency multiplied by the Planck constant, and the wavelength of a ...
. The divisor can take on either integer () or fractional () values. Here, is roughly but not exactly equal to the filling factor of Landau levels. The quantum Hall effect is referred to as the integer or fractional quantum Hall effect depending on whether is an integer or fraction, respectively.
The striking feature of the integer quantum Hall effect is the persistence of the quantization (i.e. the Hall plateau) as the electron density is varied. Since the electron density remains constant when the Fermi level
The Fermi level of a solid-state body is the thermodynamic work required to add one electron to the body. It is a thermodynamic quantity usually denoted by ''μ'' or ''E''F
for brevity. The Fermi level does not include the work required to re ...
is in a clean spectral gap, this situation corresponds to one where the Fermi level is an energy with a finite density of states, though these states are localized (see Anderson localization
In condensed matter physics, Anderson localization (also known as strong localization) is the absence of diffusion of waves in a ''disordered'' medium. This phenomenon is named after the American physicist P. W. Anderson, who was the first to su ...
).
The fractional quantum Hall effect
The fractional quantum Hall effect (fractional QHE or FQHE) is the observation of precisely quantized plateaus in the Hall conductance of 2-dimensional (2D) electrons at fractional values of e^2/h, where ''e'' is the electron charge and ''h'' i ...
is more complicated and still considered an open research problem. Its existence relies fundamentally on electron–electron interactions. In 1988, it was proposed that there was a quantum Hall effect without Landau levels. This quantum Hall effect is referred to as the quantum anomalous Hall (QAH) effect. There is also a new concept of the quantum spin Hall effect
The quantum spin Hall state is a state of matter proposed to exist in special, two-dimensional semiconductors that have a quantized spin-Hall conductance and a vanishing charge-Hall conductance. The quantum spin Hall state of matter is the cousin o ...
which is an analogue of the quantum Hall effect, where spin currents flow instead of charge currents.
Applications
Electrical resistance standards
The quantization of the Hall conductance () has the important property of being exceedingly precise. Actual measurements of the Hall conductance have been found to be integer or fractional multiples of to better than one part in a billion. It has allowed for the definition of a new practicalstandard Standard may refer to:
Symbols
* Colours, standards and guidons, kinds of military signs
* Standard (emblem), a type of a large symbol or emblem used for identification
Norms, conventions or requirements
* Standard (metrology), an object ...
for electrical resistance
The electrical resistance of an object is a measure of its opposition to the flow of electric current. Its reciprocal quantity is , measuring the ease with which an electric current passes. Electrical resistance shares some conceptual paral ...
, based on the resistance quantum given by the von Klitzing constant . This is named after Klaus von Klitzing, the discoverer of exact quantization. The quantum Hall effect also provides an extremely precise independent determination of the fine-structure constant
In physics, the fine-structure constant, also known as the Sommerfeld constant, commonly denoted by (the Alpha, Greek letter ''alpha''), is a Dimensionless physical constant, fundamental physical constant that quantifies the strength of the el ...
, a quantity of fundamental importance in quantum electrodynamics
In particle physics, quantum electrodynamics (QED) is the Theory of relativity, relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quant ...
.
In 1990, a fixed conventional value was defined for use in resistance calibrations worldwide. Later, the 2019 revision of the SI
In 2019, four of the seven SI base units specified in the International System of Quantities were redefined in terms of natural physical constants, rather than human artefacts such as the standard kilogram.
Effective 20 May 2019, the 144th ...
fixed exact values of and , resulting in an exact
Research status
The fractional quantum Hall effect is considered part of ''exact quantization''. Exact quantization in full generality is not completely understood but it has been explained as a very subtle manifestation of the combination of the principle of gauge invariance together with another symmetry (see Anomalies). The integer quantum Hall effect instead is considered a solved research problem and understood in the scope of TKNN formula and Chern–Simons Lagrangians. Thefractional quantum Hall effect
The fractional quantum Hall effect (fractional QHE or FQHE) is the observation of precisely quantized plateaus in the Hall conductance of 2-dimensional (2D) electrons at fractional values of e^2/h, where ''e'' is the electron charge and ''h'' i ...
is still considered an open research problem. The fractional quantum Hall effect can be also understood as an integer quantum Hall effect, although not of electrons but of charge–flux composites known as composite fermions. Other models to explain the fractional quantum Hall effect also exists.
Currently it is considered an open research problem because no single, confirmed and agreed list of fractional quantum numbers exists, neither a single agreed model to explain all of them, although there are such claims in the scope of composite fermions and Non Abelian Chern–Simons Lagrangians.
History
In 1957,Carl Frosch
Carl John Frosch (September 6, 1908 – May 18, 1984) was a Bell Labs researcher. With Lincoln Derrick, Lincoln Derick, Frosch discovered that silicon could be protectively coated by silicon dioxide by the right exposure to oxygen when hot, and ...
and Lincoln Derick were able to manufacture the first silicon dioxide
Silicon dioxide, also known as silica, is an oxide of silicon with the chemical formula , commonly found in nature as quartz. In many parts of the world, silica is the major constituent of sand. Silica is one of the most complex and abundan ...
field effect transistors at Bell Labs
Nokia Bell Labs, commonly referred to as ''Bell Labs'', is an American industrial research and development company owned by Finnish technology company Nokia. With headquarters located in Murray Hill, New Jersey, Murray Hill, New Jersey, the compa ...
, the first transistors in which drain and source were adjacent at the surface. Subsequently, a team demonstrated a working MOSFET
upright=1.3, Two power MOSFETs in amperes">A in the ''on'' state, dissipating up to about 100 watt">W and controlling a load of over 2000 W. A matchstick is pictured for scale.
In electronics, the metal–oxide–semiconductor field- ...
at Bell Labs 1960. This enabled physicists to study electron behavior in a nearly ideal two-dimensional gas.
In a MOSFET, conduction electrons travel in a thin surface layer, and a "gate
A gate or gateway is a point of entry to or from a space enclosed by walls. The word is derived from Proto-Germanic language, Proto-Germanic ''*gatan'', meaning an opening or passageway. Synonyms include yett (which comes from the same root w ...
" voltage controls the number of charge carriers in this layer. This allows researchers to explore quantum effects
Quantum mechanics is the fundamental physical theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is the foundation of a ...
by operating high-purity MOSFETs at liquid helium
Liquid helium is a physical state of helium at very low temperatures at standard atmospheric pressures. Liquid helium may show superfluidity.
At standard pressure, the chemical element helium exists in a liquid form only at the extremely low temp ...
temperatures.
The integer quantization of the Hall conductance was originally predicted by University of Tokyo
The University of Tokyo (, abbreviated as in Japanese and UTokyo in English) is a public research university in Bunkyō, Tokyo, Japan. Founded in 1877 as the nation's first modern university by the merger of several pre-westernisation era ins ...
researchers Tsuneya Ando, Yukio Matsumoto and Yasutada Uemura in 1975, on the basis of an approximate calculation which they themselves did not believe to be true. In 1978, the Gakushuin University
is a private university in Mejiro, Toshima, Tokyo.
The Gakushūin (or "Peers School") was established during the Meiji period to educate the children of the Japanese nobility, but back then the institution had only the primary and secondary ...
researchers Jun-ichi Wakabayashi and Shinji Kawaji subsequently observed the effect in experiments carried out on the inversion layer of MOSFETs.
In 1980, Klaus von Klitzing, working at the high magnetic field laboratory in Grenoble with silicon
Silicon is a chemical element; it has symbol Si and atomic number 14. It is a hard, brittle crystalline solid with a blue-grey metallic lustre, and is a tetravalent metalloid (sometimes considered a non-metal) and semiconductor. It is a membe ...
-based MOSFET samples developed by Michael Pepper and Gerhard Dorda, made the unexpected discovery that the Hall resistance was ''exactly'' quantized. For this finding, von Klitzing was awarded the 1985 Nobel Prize in Physics
The Nobel Prize in Physics () is an annual award given by the Royal Swedish Academy of Sciences for those who have made the most outstanding contributions to mankind in the field of physics. It is one of the five Nobel Prizes established by the ...
. A link between exact quantization and gauge invariance was subsequently proposed by Robert Laughlin, who connected the quantized conductivity to the quantized charge transport in a Thouless charge pump. Most integer quantum Hall experiments are now performed on gallium arsenide
Gallium arsenide (GaAs) is a III-V direct band gap semiconductor with a Zincblende (crystal structure), zinc blende crystal structure.
Gallium arsenide is used in the manufacture of devices such as microwave frequency integrated circuits, monoli ...
heterostructure
A heterojunction is an interface between two layers or regions of dissimilar semiconductors. These semiconducting materials have unequal band gaps as opposed to a homojunction. It is often advantageous to engineer the electronic energy bands in m ...
s, although many other semiconductor materials can be used. In 2007, the integer quantum Hall effect was reported in graphene
Graphene () is a carbon allotrope consisting of a Single-layer materials, single layer of atoms arranged in a hexagonal lattice, honeycomb planar nanostructure. The name "graphene" is derived from "graphite" and the suffix -ene, indicating ...
at temperatures as high as room temperature, and in the magnesium
Magnesium is a chemical element; it has Symbol (chemistry), symbol Mg and atomic number 12. It is a shiny gray metal having a low density, low melting point and high chemical reactivity. Like the other alkaline earth metals (group 2 ...
zinc
Zinc is a chemical element; it has symbol Zn and atomic number 30. It is a slightly brittle metal at room temperature and has a shiny-greyish appearance when oxidation is removed. It is the first element in group 12 (IIB) of the periodic tabl ...
oxide
An oxide () is a chemical compound containing at least one oxygen atom and one other element in its chemical formula. "Oxide" itself is the dianion (anion bearing a net charge of −2) of oxygen, an O2− ion with oxygen in the oxidation st ...
ZnO–Mg''x''Zn1−''x''O.
Integer quantum Hall effect
Landau levels
In two dimensions, when classical electrons are subjected to a magnetic field they follow circular cyclotron orbits. When the system is treated quantum mechanically, these orbits are quantized. To determine the values of the energy levels the Schrödinger equation must be solved. Since the system is subjected to a magnetic field, it has to be introduced as an electromagnetic vector potential in theSchrödinger equation
The Schrödinger equation is a partial differential equation that governs the wave function of a non-relativistic quantum-mechanical system. Its discovery was a significant landmark in the development of quantum mechanics. It is named after E ...
. The system considered is an electron gas that is free to move in the x and y directions, but is tightly confined in the z direction. Then, a magnetic field is applied in the z direction and according to the Landau gauge
In the physics of gauge theories, gauge fixing (also called choosing a gauge) denotes a mathematical procedure for coping with redundant degrees of freedom in field variables. By definition, a gauge theory represents each physically distinct co ...
the electromagnetic vector potential is and the scalar potential
In mathematical physics, scalar potential describes the situation where the difference in the potential energies of an object in two different positions depends only on the positions, not upon the path taken by the object in traveling from one p ...
is . Thus the Schrödinger equation for a particle of charge and effective mass in this system is:
:
where is the canonical momentum, which is replaced by the operator and is the total energy.
To solve this equation it is possible to separate it into two equations since the magnetic field just affects the movement along x and y axes. The total energy becomes then, the sum of two contributions . The corresponding equations in z axis is:
:
To simplify things, the solution is considered as an infinite well. Thus the solutions for the z direction are the energies , and the wavefunctions are sinusoidal. For the and directions, the solution of the Schrödinger equation can be chosen to be the product of a plane wave in -direction with some unknown function of , i.e., . This is because the vector potential does not depend on and the momentum operator therefore commutes with the Hamiltonian. By substituting this Ansatz into the Schrödinger equation one gets the one-dimensional harmonic oscillator
In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force ''F'' proportional to the displacement ''x'':
\vec F = -k \vec x,
where ''k'' is a positive const ...
equation centered at .
:
where is defined as the cyclotron frequency and the magnetic length. The energies are:
: ,
And the wavefunctions for the motion in the plane are given by the product of a plane wave in and Hermite polynomials
In mathematics, the Hermite polynomials are a classical orthogonal polynomial sequence.
The polynomials arise in:
* signal processing as Hermitian wavelets for wavelet transform analysis
* probability, such as the Edgeworth series, as well a ...
attenuated by the gaussian function in , which are the wavefunctions of a harmonic oscillator.
From the expression for the Landau levels one notices that the energy depends only on , not on . States with the same but different are degenerate.
Density of states
At zero field, the density of states per unit surface for the two-dimensional electron gas taking into account degeneration due to spin is independent of the energy : . As the field is turned on, the density of states collapses from the constant to aDirac comb
In mathematics, a Dirac comb (also known as sha function, impulse train or sampling function) is a periodic function, periodic Function (mathematics), function with the formula
\operatorname_(t) \ := \sum_^ \delta(t - k T)
for some given perio ...
, a series of Dirac functions, corresponding to the Landau levels separated . At finite temperature, however, the Landau levels acquire a width being the time between scattering events. Commonly it is assumed that the precise shape of Landau levels is a Gaussian or Lorentzian profile.
Another feature is that the wave functions form parallel strips in the -direction spaced equally along the -axis, along the lines of . Since there is nothing special about any direction in the -plane if the vector potential was differently chosen one should find circular symmetry.
Given a sample of dimensions and applying the periodic boundary conditions in the -direction being an integer, one gets that each parabolic potential is placed at a value .
The number of states for each Landau Level and can be calculated from the ratio between the total magnetic flux that passes through the sample and the magnetic flux corresponding to a state.
:
Thus the density of states per unit surface is
: .
Note the dependency of the density of states with the magnetic field. The larger the magnetic field is, the more states are in each Landau level. As a consequence, there is more confinement in the system since fewer energy levels are occupied.
Rewriting the last expression as it is clear that each Landau level contains as many states as in a 2DEG
A two-dimensional electron gas (2DEG) is a scientific model in solid-state physics. It is an Fermi gas, electron gas that is free to move in two dimensions, but tightly confined in the third. This tight confinement leads to quantized energy levels ...
in a .
Given the fact that electrons are fermions
In particle physics, a fermion is a subatomic particle that follows Fermi–Dirac statistics. Fermions have a half-integer spin ( spin , spin , etc.) and obey the Pauli exclusion principle. These particles include all quarks and leptons and ...
, for each state available in the Landau levels it corresponds to two electrons, one electron with each value for the spin
Spin or spinning most often refers to:
* Spin (physics) or particle spin, a fundamental property of elementary particles
* Spin quantum number, a number which defines the value of a particle's spin
* Spinning (textiles), the creation of yarn or thr ...
. However, if a large magnetic field is applied, the energies split into two levels due to the magnetic moment associated with the alignment of the spin with the magnetic field. The difference in the energies is being a factor which depends on the material ( for free electrons) and the Bohr magneton
In atomic physics, the Bohr magneton (symbol ) is a physical constant and the natural unit for expressing the magnetic moment of an electron caused by its orbital or spin angular momentum.
In SI units, the Bohr magneton is defined as
\mu_\mat ...
. The sign is taken when the spin is parallel to the field and when it is antiparallel. This fact called spin splitting implies that the density of states
In condensed matter physics, the density of states (DOS) of a system describes the number of allowed modes or quantum state, states per unit energy range. The density of states is defined as where N(E)\delta E is the number of states in the syste ...
for each level is reduced by a half. Note that is proportional to the magnetic field so, the larger the magnetic field is, the more relevant is the split.
 In order to get the number of occupied Landau levels, one defines the so-called filling factor as the ratio between the density of states in a 2DEG and the density of states in the Landau levels.
:
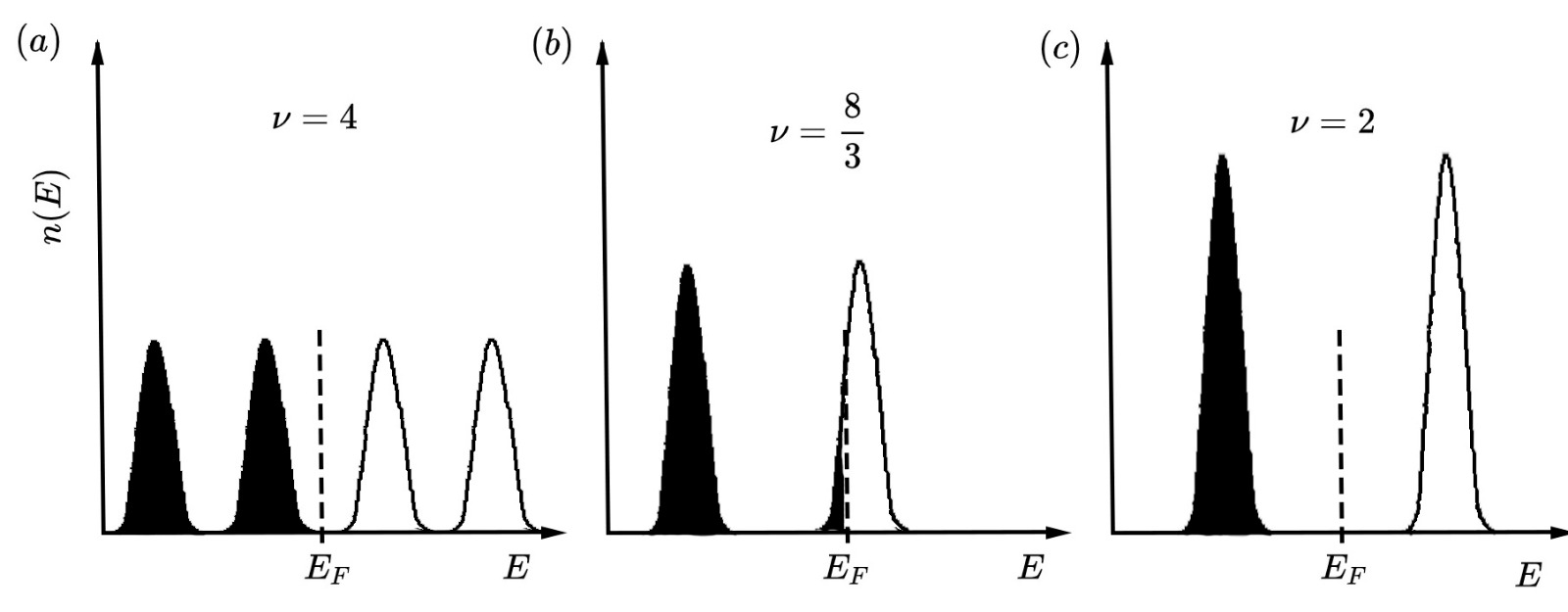
In general the filling factor is not an integer. It happens to be an integer when there is an exact number of filled Landau levels. Instead, it becomes a non-integer when the top level is not fully occupied. In actual experiments, one varies the magnetic field and fixes electron density (and not the Fermi energy!) or varies the electron density and fixes the magnetic field. Both cases correspond to a continuous variation of the filling factor and one cannot expect to be an integer. Since , by increasing the magnetic field, the Landau levels move up in energy and the number of states in each level grow, so fewer electrons occupy the top level until it becomes empty. If the magnetic field keeps increasing, eventually, all electrons will be in the lowest Landau level () and this is called the magnetic quantum limit.
In order to get the number of occupied Landau levels, one defines the so-called filling factor as the ratio between the density of states in a 2DEG and the density of states in the Landau levels.
:
In general the filling factor is not an integer. It happens to be an integer when there is an exact number of filled Landau levels. Instead, it becomes a non-integer when the top level is not fully occupied. In actual experiments, one varies the magnetic field and fixes electron density (and not the Fermi energy!) or varies the electron density and fixes the magnetic field. Both cases correspond to a continuous variation of the filling factor and one cannot expect to be an integer. Since , by increasing the magnetic field, the Landau levels move up in energy and the number of states in each level grow, so fewer electrons occupy the top level until it becomes empty. If the magnetic field keeps increasing, eventually, all electrons will be in the lowest Landau level () and this is called the magnetic quantum limit.

Longitudinal resistivity
It is possible to relate the filling factor to the resistivity and hence, to the conductivity of the system. When is an integer, theFermi energy
The Fermi energy is a concept in quantum mechanics usually referring to the energy difference between the highest and lowest occupied single-particle states in a quantum system of non-interacting fermions at absolute zero temperature.
In a Fermi ga ...
lies in between Landau levels where there are no states available for carriers, so the conductivity becomes zero (it is considered that the magnetic field is big enough so that there is no overlap between Landau levels, otherwise there would be few electrons and the conductivity would be approximately ). Consequently, the resistivity becomes zero too (At very high magnetic fields it is proven that longitudinal conductivity and resistivity are proportional).
With the conductivity one finds
:
If the longitudinal resistivity is zero and transversal is finite, then . Thus both the longitudinal conductivity and resistivity become zero.
Instead, when is a half-integer, the Fermi energy is located at the peak of the density distribution of some Landau Level. This means that the conductivity will have a maximum .
This distribution of minimums and maximums corresponds to ¨quantum oscillations¨ called ''Shubnikov–de Haas oscillations'' which become more relevant as the magnetic field increases. Obviously, the height of the peaks are larger as the magnetic field increases since the density of states increases with the field, so there are more carriers which contribute to the resistivity. It is interesting to notice that if the magnetic field is very small, the longitudinal resistivity is a constant which means that the classical result is reached.

Transverse resistivity
From the classical relation of the transverse resistivity and substituting one finds out the quantization of the transverse resistivity and conductivity: : One concludes then, that the transverse resistivity is a multiple of the inverse of the so-called conductance quantum if the filling factor is an integer. In experiments, however, plateaus are observed for whole plateaus of filling values , which indicates that there are in fact electron states between the Landau levels. These states are localized in, for example, impurities of the material where they are trapped in orbits so they can not contribute to the conductivity. That is why the resistivity remains constant in between Landau levels. Again if the magnetic field decreases, one gets the classical result in which the resistivity is proportional to the magnetic field.Photonic quantum Hall effect
The quantum Hall effect, in addition to being observed in two-dimensional electron systems, can be observed in photons.Photon
A photon () is an elementary particle that is a quantum of the electromagnetic field, including electromagnetic radiation such as light and radio waves, and the force carrier for the electromagnetic force. Photons are massless particles that can ...
s do not possess inherent electric charge
Electric charge (symbol ''q'', sometimes ''Q'') is a physical property of matter that causes it to experience a force when placed in an electromagnetic field. Electric charge can be ''positive'' or ''negative''. Like charges repel each other and ...
, but through the manipulation of discrete optical resonators and coupling phases or on-site phases, an artificial magnetic field
A magnetic field (sometimes called B-field) is a physical field that describes the magnetic influence on moving electric charges, electric currents, and magnetic materials. A moving charge in a magnetic field experiences a force perpendicular ...
can be created. This process can be expressed through a metaphor of photons bouncing between multiple mirrors. By shooting the light across multiple mirrors, the photons are routed and gain additional phase proportional to their angular momentum
Angular momentum (sometimes called moment of momentum or rotational momentum) is the rotational analog of Momentum, linear momentum. It is an important physical quantity because it is a Conservation law, conserved quantity – the total ang ...
. This creates an effect like they are in a magnetic field
A magnetic field (sometimes called B-field) is a physical field that describes the magnetic influence on moving electric charges, electric currents, and magnetic materials. A moving charge in a magnetic field experiences a force perpendicular ...
.
Topological classification
The integers that appear in the Hall effect are examples oftopological quantum number
In physics, a topological quantum number (also called topological charge) is any quantity, in a physical theory, that takes on only one of a discrete set of values, due to topological considerations. Most commonly, topological quantum numbers ar ...
s. They are known in mathematics as the first Chern numbers and are closely related to Berry's phase
In Classical mechanics, classical and quantum mechanics, geometric phase is a Phase (waves), phase difference acquired over the course of a Period (physics), cycle, when a system is subjected to cyclic adiabatic process (quantum mechanics), adiabat ...
. A striking model of much interest in this context is the Azbel–Harper–Hofstadter model whose quantum phase diagram is the Hofstadter butterfly shown in the figure. The vertical axis is the strength of the magnetic field
A magnetic field (sometimes called B-field) is a physical field that describes the magnetic influence on moving electric charges, electric currents, and magnetic materials. A moving charge in a magnetic field experiences a force perpendicular ...
and the horizontal axis is the chemical potential
In thermodynamics, the chemical potential of a Chemical specie, species is the energy that can be absorbed or released due to a change of the particle number of the given species, e.g. in a chemical reaction or phase transition. The chemical potent ...
, which fixes the electron density. The colors represent the integer Hall conductances. Warm colors represent positive integers and cold colors negative integers. Note, however, that the density of states in these regions of quantized Hall conductance is zero; hence, they cannot produce the plateaus observed in the experiments. The phase diagram is fractal and has structure on all scales. In the figure there is an obvious self-similarity
In mathematics, a self-similar object is exactly or approximately similar to a part of itself (i.e., the whole has the same shape as one or more of the parts). Many objects in the real world, such as coastlines, are statistically self-similar ...
. In the presence of disorder, which is the source of the plateaus seen in the experiments, this diagram is very different and the fractal structure is mostly washed away. Also, the experiments control the filling factor and not the Fermi energy. If this diagram is plotted as a function of filling factor, all the features are completely washed away, hence, it has very little to do with the actual Hall physics.
Concerning physical mechanisms, impurities and/or particular states (e.g., edge currents) are important for both the 'integer' and 'fractional' effects. In addition, Coulomb interaction is also essential in the fractional quantum Hall effect
The fractional quantum Hall effect (fractional QHE or FQHE) is the observation of precisely quantized plateaus in the Hall conductance of 2-dimensional (2D) electrons at fractional values of e^2/h, where ''e'' is the electron charge and ''h'' i ...
. The observed strong similarity between integer and fractional quantum Hall effects is explained by the tendency of electrons to form bound states with an even number of magnetic flux quanta, called '' composite fermions''.
Bohr atom interpretation of the von Klitzing constant
The value of the von Klitzing constant may be obtained already on the level of a single atom within theBohr model
In atomic physics, the Bohr model or Rutherford–Bohr model was a model of the atom that incorporated some early quantum concepts. Developed from 1911 to 1918 by Niels Bohr and building on Ernest Rutherford's nuclear Rutherford model, model, i ...
while looking at it as a single-electron Hall effect. While during the cyclotron motion
In physics, cyclotron motion, also known as gyromotion, refers to the circular motion exhibited by charged particles in a uniform magnetic field.
The circular trajectory of a particle in cyclotron motion is characterized by an angular frequency r ...
on a circular orbit the centrifugal force is balanced by the Lorentz force
In electromagnetism, the Lorentz force is the force exerted on a charged particle by electric and magnetic fields. It determines how charged particles move in electromagnetic environments and underlies many physical phenomena, from the operation ...
responsible for the transverse induced voltage and the Hall effect, one may look at the Coulomb potential difference in the Bohr atom as the induced single atom Hall voltage and the periodic electron motion on a circle as a Hall current. Defining the single atom Hall current as a rate a single electron charge is making Kepler revolutions with angular frequency
:
and the induced Hall voltage as a difference between the hydrogen nucleus Coulomb potential at the electron orbital point and at infinity:
:
One obtains the quantization of the defined Bohr orbit Hall resistance in steps of the von Klitzing constant as
:
which for the Bohr atom is linear but not inverse in the integer ''n''.
Relativistic analogs
Relativistic examples of the integer quantum Hall effect andquantum spin Hall effect
The quantum spin Hall state is a state of matter proposed to exist in special, two-dimensional semiconductors that have a quantized spin-Hall conductance and a vanishing charge-Hall conductance. The quantum spin Hall state of matter is the cousin o ...
arise in the context of lattice gauge theory
In physics, lattice gauge theory is the study of gauge theories on a spacetime that has been discretized into a lattice.
Gauge theories are important in particle physics, and include the prevailing theories of elementary particles: quantum ele ...
.
See also
* Quantum Hall transitions *Fractional quantum Hall effect
The fractional quantum Hall effect (fractional QHE or FQHE) is the observation of precisely quantized plateaus in the Hall conductance of 2-dimensional (2D) electrons at fractional values of e^2/h, where ''e'' is the electron charge and ''h'' i ...
* Quantum anomalous Hall effect
* Quantum cellular automata
* Composite fermions
* Conductance Quantum
The conductance quantum, denoted by the symbol , is the quantized unit of electrical conductance. It is defined by the elementary charge ''e'' and Planck constant ''h'' as:
: G_0 = \frac = 4 \alpha \epsilon_0 c =
It appears when measuring the co ...
* Hall effect
The Hall effect is the production of a voltage, potential difference (the Hall voltage) across an electrical conductor that is wikt:transverse, transverse to an electric current in the conductor and to an applied magnetic field wikt:perpendicul ...
* Hall probe
* Graphene
Graphene () is a carbon allotrope consisting of a Single-layer materials, single layer of atoms arranged in a hexagonal lattice, honeycomb planar nanostructure. The name "graphene" is derived from "graphite" and the suffix -ene, indicating ...
* Quantum spin Hall effect
The quantum spin Hall state is a state of matter proposed to exist in special, two-dimensional semiconductors that have a quantized spin-Hall conductance and a vanishing charge-Hall conductance. The quantum spin Hall state of matter is the cousin o ...
* Coulomb potential between two current loops embedded in a magnetic field
References
Further reading
* * * ''25 years of Quantum Hall Effect'', K. von Klitzing, Poincaré Seminar (Paris-2004)Postscript
* Magnet Lab Press Releas
* * Zyun F. Ezawa
''Quantum Hall Effects - Field Theoretical Approach and Related Topics.''
World Scientific, Singapore 2008, * Sankar D. Sarma, Aron Pinczuk: ''Perspectives in Quantum Hall Effects.'' Wiley-VCH, Weinheim 2004, * * E. I. Rashba and V. B. Timofeev, Quantum Hall Effect, Sov. Phys. – Semiconductors v. 20, pp. 617–647 (1986). {{Authority control Hall effect Condensed matter physics Quantum electronics Spintronics Quantum phases Mesoscopic physics Articles containing video clips 1980 in science