|
Gauss–Markov Theorem
In statistics, the Gauss–Markov theorem (or simply Gauss theorem for some authors) states that the ordinary least squares (OLS) estimator has the lowest sampling variance within the class of linear unbiased estimators, if the errors in the linear regression model are uncorrelated, have equal variances and expectation value of zero. The errors do not need to be normal, nor do they need to be independent and identically distributed (only uncorrelated with mean zero and homoscedastic with finite variance). The requirement that the estimator be unbiased cannot be dropped, since biased estimators exist with lower variance. See, for example, the James–Stein estimator (which also drops linearity), ridge regression, or simply any degenerate estimator. The theorem was named after Carl Friedrich Gauss and Andrey Markov, although Gauss' work significantly predates Markov's. But while Gauss derived the result under the assumption of independence and normality, Markov r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German language, German: ', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of statistical survey, surveys and experimental design, experiments. When census data (comprising every member of the target population) cannot be collected, statisticians collect data by developing specific experiment designs and survey sample (statistics), samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Carl Friedrich Gauss
Johann Carl Friedrich Gauss (; ; ; 30 April 177723 February 1855) was a German mathematician, astronomer, geodesist, and physicist, who contributed to many fields in mathematics and science. He was director of the Göttingen Observatory and professor of astronomy from 1807 until his death in 1855. While studying at the University of Göttingen, he propounded several mathematical theorems. As an independent scholar, he wrote the masterpieces '' Disquisitiones Arithmeticae'' and ''Theoria motus corporum coelestium''. Gauss produced the second and third complete proofs of the fundamental theorem of algebra. In number theory, he made numerous contributions, such as the composition law, the law of quadratic reciprocity and the Fermat polygonal number theorem. He also contributed to the theory of binary and ternary quadratic forms, the construction of the heptadecagon, and the theory of hypergeometric series. Due to Gauss' extensive and fundamental contributions to science ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Design Matrix
In statistics and in particular in regression analysis, a design matrix, also known as model matrix or regressor matrix and often denoted by X, is a matrix of values of explanatory variables of a set of objects. Each row represents an individual object, with the successive columns corresponding to the variables and their specific values for that object. The design matrix is used in certain statistical models, e.g., the general linear model. It can contain indicator variables (ones and zeros) that indicate group membership in an ANOVA, or it can contain values of continuous variables. The design matrix contains data on the independent variables (also called explanatory variables), in a statistical model that is intended to explain observed data on a response variable (often called a dependent variable). The theory relating to such models uses the design matrix as input to some linear algebra : see for example linear regression. A notable feature of the concept of a design matrix i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generalized Least Squares
In statistics, generalized least squares (GLS) is a method used to estimate the unknown parameters in a Linear regression, linear regression model. It is used when there is a non-zero amount of correlation between the Residual (statistics), residuals in the regression model. GLS is employed to improve efficiency_(statistics), statistical efficiency and reduce the risk of drawing erroneous inferences, as compared to conventional least squares and weighted least squares methods. It was first described by Alexander Aitken in 1935. It requires knowledge of the covariance matrix for the residuals. If this is unknown, estimating the covariance matrix gives the method of feasible generalized least squares (FGLS). However, FGLS provides fewer guarantees of improvement. Method In standard linear regression models, one observes data \_ on ''n'' statistical units with ''k'' − 1 predictor values and one response value each. The response values are placed in a vector,\mathbf ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hessian Matrix
In mathematics, the Hessian matrix, Hessian or (less commonly) Hesse matrix is a square matrix of second-order partial derivatives of a scalar-valued Function (mathematics), function, or scalar field. It describes the local curvature of a function of many variables. The Hessian matrix was developed in the 19th century by the German mathematician Otto Hesse, Ludwig Otto Hesse and later named after him. Hesse originally used the term "functional determinants". The Hessian is sometimes denoted by H or \nabla\nabla or \nabla^2 or \nabla\otimes\nabla or D^2. Definitions and properties Suppose f : \R^n \to \R is a function taking as input a vector \mathbf \in \R^n and outputting a scalar f(\mathbf) \in \R. If all second-order partial derivatives of f exist, then the Hessian matrix \mathbf of f is a square n \times n matrix, usually defined and arranged as \mathbf H_f= \begin \dfrac & \dfrac & \cdots & \dfrac \\[2.2ex] \dfrac & \dfrac & \cdots & \dfrac \\[2.2ex] \vdots & \vdot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transpose
In linear algebra, the transpose of a Matrix (mathematics), matrix is an operator which flips a matrix over its diagonal; that is, it switches the row and column indices of the matrix by producing another matrix, often denoted by (among other notations). The transpose of a matrix was introduced in 1858 by the British mathematician Arthur Cayley. Transpose of a matrix Definition The transpose of a matrix , denoted by , , , A^, , , or , may be constructed by any one of the following methods: #Reflection (mathematics), Reflect over its main diagonal (which runs from top-left to bottom-right) to obtain #Write the rows of as the columns of #Write the columns of as the rows of Formally, the -th row, -th column element of is the -th row, -th column element of : :\left[\mathbf^\operatorname\right]_ = \left[\mathbf\right]_. If is an matrix, then is an matrix. In the case of square matrices, may also denote the th power of the matrix . For avoiding a possibl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mean Squared Error
In statistics, the mean squared error (MSE) or mean squared deviation (MSD) of an estimator (of a procedure for estimating an unobserved quantity) measures the average of the squares of the errors—that is, the average squared difference between the estimated values and the true value. MSE is a risk function, corresponding to the expected value of the squared error loss. The fact that MSE is almost always strictly positive (and not zero) is because of randomness or because the estimator does not account for information that could produce a more accurate estimate. In machine learning, specifically empirical risk minimization, MSE may refer to the ''empirical'' risk (the average loss on an observed data set), as an estimate of the true MSE (the true risk: the average loss on the actual population distribution). The MSE is a measure of the quality of an estimator. As it is derived from the square of Euclidean distance, it is always a positive value that decreases as the erro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
If And Only If
In logic and related fields such as mathematics and philosophy, "if and only if" (often shortened as "iff") is paraphrased by the biconditional, a logical connective between statements. The biconditional is true in two cases, where either both statements are true or both are false. The connective is biconditional (a statement of material equivalence), and can be likened to the standard material conditional ("only if", equal to "if ... then") combined with its reverse ("if"); hence the name. The result is that the truth of either one of the connected statements requires the truth of the other (i.e. either both statements are true, or both are false), though it is controversial whether the connective thus defined is properly rendered by the English "if and only if"—with its pre-existing meaning. For example, ''P if and only if Q'' means that ''P'' is true whenever ''Q'' is true, and the only case in which ''P'' is true is if ''Q'' is also true, whereas in the case of ''P if Q ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Regression
In statistics, linear regression is a statistical model, model that estimates the relationship between a Scalar (mathematics), scalar response (dependent variable) and one or more explanatory variables (regressor or independent variable). A model with exactly one explanatory variable is a ''simple linear regression''; a model with two or more explanatory variables is a multiple linear regression. This term is distinct from multivariate linear regression, which predicts multiple correlated dependent variables rather than a single dependent variable. In linear regression, the relationships are modeled using linear predictor functions whose unknown model parameters are estimation theory, estimated from the data. Most commonly, the conditional mean of the response given the values of the explanatory variables (or predictors) is assumed to be an affine function of those values; less commonly, the conditional median or some other quantile is used. Like all forms of regression analysis, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
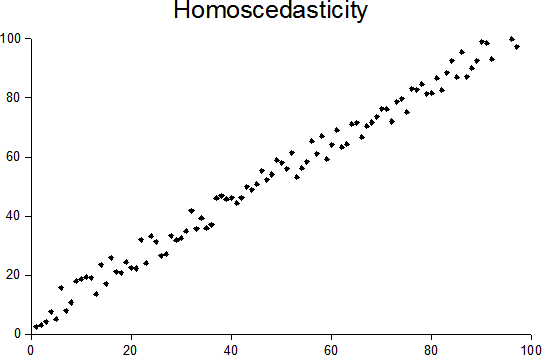
Homoscedasticity
In statistics, a sequence of random variables is homoscedastic () if all its random variables have the same finite variance; this is also known as homogeneity of variance. The complementary notion is called heteroscedasticity, also known as heterogeneity of variance. The spellings ''homoskedasticity'' and ''heteroskedasticity'' are also frequently used. “Skedasticity” comes from the Ancient Greek word “skedánnymi”, meaning “to scatter”. Assuming a variable is homoscedastic when in reality it is heteroscedastic () results in Biased estimator, unbiased but Efficiency (statistics), inefficient point estimates and in biased estimates of standard errors, and may result in overestimating the goodness of fit as measured by the Pearson product-moment correlation coefficient, Pearson coefficient. The existence of heteroscedasticity is a major concern in regression analysis and the analysis of variance, as it invalidates statistical hypothesis testing, statistical tests ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Errors And Residuals In Statistics
In statistics and optimization, errors and residuals are two closely related and easily confused measures of the deviation of an observed value of an element of a statistical sample from its "true value" (not necessarily observable). The error of an observation is the deviation of the observed value from the true value of a quantity of interest (for example, a population mean). The residual is the difference between the observed value and the '' estimated'' value of the quantity of interest (for example, a sample mean). The distinction is most important in regression analysis, where the concepts are sometimes called the regression errors and regression residuals and where they lead to the concept of studentized residuals. In econometrics, "errors" are also called disturbances. Introduction Suppose there is a series of observations from a univariate distribution and we want to estimate the mean of that distribution (the so-called location model). In this case, the errors a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alexander Aitken
Alexander Craig "Alec" Aitken (1 April 1895 – 3 November 1967) was one of New Zealand's most eminent mathematicians. In a 1935 paper he introduced the concept of generalized least squares, along with now standard vector/matrix notation for the linear regression model. Another influential paper co-authored with his student Harold Silverstone established the lower bound on the variance of an estimator, now known as Cramér–Rao bound. He was elected to the Royal Society of Literature for his World War I memoir, ''Gallipoli to the Somme''. Life and work Aitken was born on 1 April 1895 in Dunedin, the eldest of the seven children of Elizabeth Towers and William Aitken. He was of Scottish descent, his grandfather having emigrated from Lanarkshire in 1868. His mother was from Wolverhampton. He was educated at Otago Boys' High School in Dunedin (1908–13) where he was school dux and won the Thomas Baker Calculus Scholarship in his last year at school. He saw active serv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |