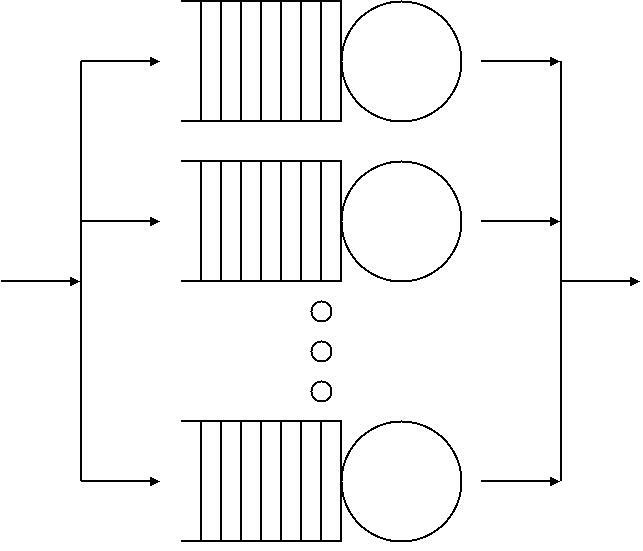
|
Flow-equivalent Server Method
In queueing theory, a discipline within the mathematical theory of probability, the flow-equivalent server method (also known as flow-equivalent aggregation technique, Norton's theorem for queueing networks or the Chandy–Herzog–Woo method) is a divide-and-conquer method to solve product form queueing networks inspired by Norton's theorem for electrical circuits. The network is successively split into two, one portion is reconfigured to a closed network and evaluated. Marie's algorithm is a similar method where analysis of the sub-network are performed with state-dependent Poisson process In probability theory, statistics and related fields, a Poisson point process (also known as: Poisson random measure, Poisson random point field and Poisson point field) is a type of mathematical object that consists of Point (geometry), points ... arrivals. References Queueing theory {{Probability-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Queueing Theory
Queueing theory is the mathematical study of waiting lines, or queues. A queueing model is constructed so that queue lengths and waiting time can be predicted. Queueing theory is generally considered a branch of operations research because the results are often used when making business decisions about the resources needed to provide a service. Queueing theory has its origins in research by Agner Krarup Erlang, who created models to describe the system of incoming calls at the Copenhagen Telephone Exchange Company. These ideas were seminal to the field of teletraffic engineering and have since seen applications in telecommunications, traffic engineering, computing, project management, and particularly industrial engineering, where they are applied in the design of factories, shops, offices, and hospitals. Spelling The spelling "queueing" over "queuing" is typically encountered in the academic research field. In fact, one of the flagship journals of the field is '' Queue ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Queueing Systems
''Queueing Systems'' is a peer-reviewed scientific journal covering queueing theory. It is published by Springer Science+Business Media. The current editor-in-chief is Sergey Foss. According to the ''Journal Citation Reports'', the journal has a 2019 impact factor of 1.114. Editors-in-chief N. U. Prabhu was the founding editor-in-chief when the journal was established in 1986 and remained editor until 1995. Richard F. Serfozo was editor from 1996 to 2004, and Onno J. Boxma from 2004 to 2009. Since 2009, the editor has been Sergey Foss. Abstracting and indexing ''Queueing Systems'' is abstracted and indexed in DBLP, Journal Citation Reports, Mathematical Reviews, Research Papers in Economics, SCImago Journal Rank, Scopus, Science Citation Index, Zentralblatt MATH zbMATH Open, formerly Zentralblatt MATH, is a major reviewing service providing reviews and abstracts for articles in pure and applied mathematics, produced by the Berlin office of FIZ Karlsruhe – Leibniz Ins ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Divide-and-conquer Method
In computer science, divide and conquer is an algorithm design paradigm. A divide-and-conquer algorithm recursively breaks down a problem into two or more sub-problems of the same or related type, until these become simple enough to be solved directly. The solutions to the sub-problems are then combined to give a solution to the original problem. The divide-and-conquer technique is the basis of efficient algorithms for many problems, such as sorting (e.g., quicksort, merge sort), multiplying large numbers (e.g., the Karatsuba algorithm), finding the closest pair of points, syntactic analysis (e.g., top-down parsers), and computing the discrete Fourier transform ( FFT). Designing efficient divide-and-conquer algorithms can be difficult. As in mathematical induction, it is often necessary to generalize the problem to make it amenable to a recursive solution. The correctness of a divide-and-conquer algorithm is usually proved by mathematical induction, and its computational cost ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Product Form Queueing Network
In probability theory, a product-form solution is a particularly efficient form of solution for determining some metric of a system with distinct sub-components, where the metric for the collection of components can be written as a product of the metric across the different components. Using capital Pi notation a product-form solution has algebraic form :\text(x_1,x_2,x_3,\ldots,x_n) = B \prod_^n \text(x_i) where ''B'' is some constant. Solutions of this form are of interest as they are computationally inexpensive to evaluate for large values of ''n''. Such solutions in queueing networks are important for finding performance metrics in models of multiprogrammed and time-shared computer systems. Equilibrium distributions The first product-form solutions were found for equilibrium distributions of Markov chains. Trivially, models composed of two or more independent sub-components exhibit a product-form solution by the definition of independence. Initially the term was used in que ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Norton's Theorem
In Direct current, direct-current circuit theory, Norton's theorem, also called the Mayer–Norton theorem, is a simplification that can be applied to Electrical network, networks made of Linear time-invariant system, linear time-invariant Resistor, resistances, Voltage source, voltage sources, and Current source, current sources. At a pair of terminals of the network, it can be replaced by a current source and a single resistor in parallel. For alternating current (AC) systems the theorem can be applied to Reactive power, reactive Electrical impedance, impedances as well as resistances. The Norton equivalent circuit is used to represent any network of linear sources and impedances at a given frequency. Norton's theorem and its dual, Thévenin's theorem, are widely used for circuit analysis simplification and to study circuit's Initial condition, initial-condition and Steady state (electronics), steady-state response. Norton's theorem was independently derived in 1926 by Siem ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Poisson Process
In probability theory, statistics and related fields, a Poisson point process (also known as: Poisson random measure, Poisson random point field and Poisson point field) is a type of mathematical object that consists of Point (geometry), points randomly located on a Space (mathematics), mathematical space with the essential feature that the points occur independently of one another. The process's name derives from the fact that the number of points in any given finite region follows a Poisson distribution. The process and the distribution are named after French mathematician Siméon Denis Poisson. The process itself was discovered independently and repeatedly in several settings, including experiments on radioactive decay, telephone call arrivals and actuarial science. This point process is used as a mathematical model for seemingly random processes in numerous disciplines including astronomy,G. J. Babu and E. D. Feigelson. Spatial point processes in astronomy. ''Journal of st ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |