|
Feedback Arc Set
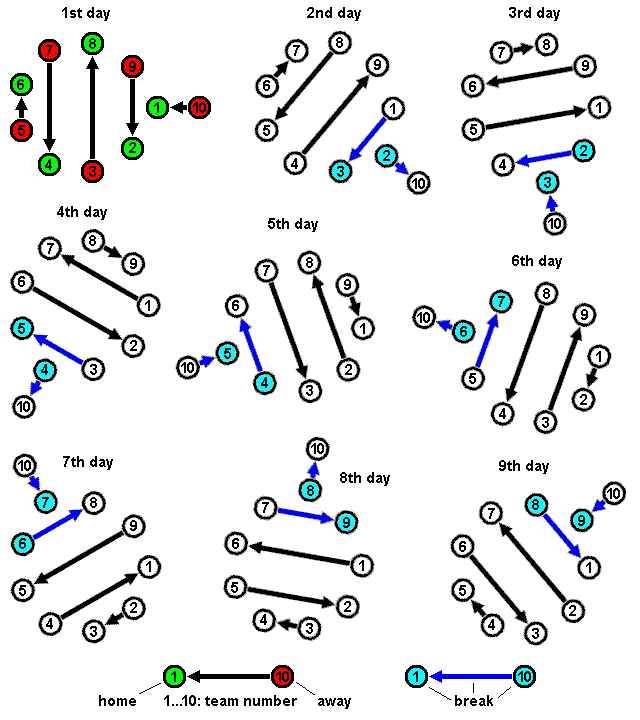
In graph theory and graph algorithms, a feedback arc set or feedback edge set in a directed graph is a subset of the edges of the graph that contains at least one edge out of every cycle in the graph. Removing these edges from the graph breaks all of the cycles, producing an acyclic subgraph of the given graph, often called a directed acyclic graph. A feedback arc set with the fewest possible edges is a minimum feedback arc set and its removal leaves a maximum acyclic subgraph; weighted versions of these optimization problems are also used. If a feedback arc set is minimal, meaning that removing any edge from it produces a subset that is not a feedback arc set, then it has an additional property: reversing all of its edges, rather than removing them, produces a directed acyclic graph. Feedback arc sets have applications in circuit analysis, chemical engineering, deadlock resolution, ranked voting, ranking competitors in sporting events, mathematical psychology, ethology, and grap ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inapproximability
In computer science, hardness of approximation is a field that studies the Computational complexity theory, algorithmic complexity of finding near-optimal solutions to optimization problems. Scope Hardness of approximation complements the study of approximation algorithms by proving, for certain problems, a limit on the factors with which their solution can be efficiently approximated. Typically such limits show a factor of approximation beyond which a problem becomes NP-hard, implying that finding a polynomial time approximation for the problem is impossible unless NP=P. Some hardness of approximation results, however, are based on other hypotheses, a notable one among which is the unique games conjecture. History Since the early 1970s it was known that many optimization problems could not be solved in polynomial time unless P = NP, but in many of these problems the optimal solution could be efficiently approximated to a certain degree. In the 1970s, Teofilo F. Gonzalez and Sartaj ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dominance Hierarchy
In the zoological field of ethology, a dominance hierarchy (formerly and colloquially called a pecking order) is a type of social hierarchy that arises when members of animal social animal, social groups interact, creating a ranking system. Different types of interactions can result in dominance depending on the species, including Ritualized aggression, ritualized displays of aggression or direct physical violence. In social living groups, members are likely to compete for access to limited resources and mating opportunities. Rather than fighting each time they meet, individuals of the same sex establish a relative rank, with higher-ranking individuals often gaining more access to resources and mates. Based on repetitive interactions, a social order is created that is subject to change each time a dominant animal is challenged by a subordinate one. Definitions Dominance is an individual's preferential access to resources over another based on coercive capacity based on streng ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Primatology
Primatology is the scientific study of non-human primates. It is a diverse discipline at the boundary between mammalogy and anthropology, and researchers can be found in academic departments of anatomy, anthropology, biology, medicine, psychology, veterinary sciences and zoology, as well as in animal sanctuaries, biomedical research facilities, museums and zoos. Primatologists study both living and extinct primates in their natural habitats and in laboratories by conducting field studies and experiments in order to understand aspects of their evolution and behavior. Sub-disciplines As a science, primatology has many different sub-disciplines which vary in terms of theoretical and methodological approaches to the subject used in researching extant primates and their extinct ancestors. There are two main centers of primatology, Western primatology and Japanese primatology. These two divergent disciplines stem from the unique cultural backgrounds and philosophies that went int ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Group Tournament Ranking System
In a group tournament, unlike a knockout tournament, there is no scheduled decisive final match. Instead, all the competitors are ranked by examining the results of all the matches played in the tournament. Typically, points are awarded for each match,A match for the purposes of a tournament (also called a '' tie'', '' fixture'', or ''rubber'') may comprise multiple individual matches in the sport or game concerned (also called ''rubbers'' or ''legs''). with competitors ranked based either on total number of points or average points per match. A special type of group tournament is the Round-robin tournament, in which each player plays against every other player. Usually each competitor finishes with an equal number of matches, in which case rankings by total points and by average points are equivalent at the end of the tournament, though not necessarily while it is in progress. Examples with unequal numbers of matches include the 1895 County Championship in English cricket, an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Round-robin Tournament
A round-robin tournament or all-play-all tournament is a competition format in which each contestant meets every other participant, usually in turn.''Webster's Third New International Dictionary of the English Language, Unabridged'' (1971, G. & C. Merriam Co), p.1980. A round-robin contrasts with an elimination tournament, wherein participants are eliminated after a certain number of wins or losses. Terminology The term ''round-robin'' is derived from the French term ('ribbon'). Over time, the term became idiomized to ''robin''. In a ''single round-robin'' schedule, each participant plays every other participant once. If each participant plays all others twice, this is frequently called a ''double round-robin''. The term is rarely used when all participants play one another more than twice, and is never used when one participant plays others an unequal number of times, as is the case in almost all of the major North American professional sports leagues. In the United Kingdom, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Topological Sorting
In computer science, a topological sort or topological ordering of a directed graph is a linear ordering of its vertices such that for every directed edge ''(u,v)'' from vertex ''u'' to vertex ''v'', ''u'' comes before ''v'' in the ordering. For instance, the vertices of the graph may represent tasks to be performed, and the edges may represent constraints that one task must be performed before another; in this application, a topological ordering is just a valid sequence for the tasks. Precisely, a topological sort is a graph traversal in which each node ''v'' is visited only after all its dependencies are visited''.'' A topological ordering is possible if and only if the graph has no directed cycles, that is, if it is a directed acyclic graph (DAG). Any DAG has at least one topological ordering, and there are linear time algorithms for constructing it. Topological sorting has many applications, especially in ranking problems such as feedback arc set. Topological sorting is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circuit Rank
In graph theory, a branch of mathematics, the cyclomatic number, circuit rank, cycle rank, or nullity of an undirected graph is the minimum number of edges that must be removed from the graph to break all its cycles, making it into a tree or forest. Formula The cyclomatic number of a graph equals the number of independent cycles in the graph, the size of a cycle basis. Unlike the corresponding feedback arc set problem for directed graphs, the cyclomatic number is easily computed using the formula: r = e - v + c, where is the number of edges in the given graph, is the number of vertices, and is the number of connected components. . It is possible to construct a minimum-size set of edges that breaks all cycles efficiently, either using a greedy algorithm or by complementing a spanning forest. The cyclomatic number can be explained in terms of algebraic graph theory as the dimension of the cycle space of a graph, in terms of matroid theory as the corank of a graphic m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spanning Tree
In the mathematical field of graph theory, a spanning tree ''T'' of an undirected graph ''G'' is a subgraph that is a tree which includes all of the vertices of ''G''. In general, a graph may have several spanning trees, but a graph that is not connected will not contain a spanning tree (see about spanning forests below). If all of the edges of ''G'' are also edges of a spanning tree ''T'' of ''G'', then ''G'' is a tree and is identical to ''T'' (that is, a tree has a unique spanning tree and it is itself). Applications Several pathfinding algorithms, including Dijkstra's algorithm and the A* search algorithm, internally build a spanning tree as an intermediate step in solving the problem. In order to minimize the cost of power networks, wiring connections, piping, automatic speech recognition, etc., people often use algorithms that gradually build a spanning tree (or many such trees) as intermediate steps in the process of finding the minimum spanning tree. The Intern ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Undirected Graph
In discrete mathematics, particularly in graph theory, a graph is a structure consisting of a set of objects where some pairs of the objects are in some sense "related". The objects are represented by abstractions called '' vertices'' (also called ''nodes'' or ''points'') and each of the related pairs of vertices is called an ''edge'' (also called ''link'' or ''line''). Typically, a graph is depicted in diagrammatic form as a set of dots or circles for the vertices, joined by lines or curves for the edges. The edges may be directed or undirected. For example, if the vertices represent people at a party, and there is an edge between two people if they shake hands, then this graph is undirected because any person ''A'' can shake hands with a person ''B'' only if ''B'' also shakes hands with ''A''. In contrast, if an edge from a person ''A'' to a person ''B'' means that ''A'' owes money to ''B'', then this graph is directed, because owing money is not necessarily reciprocated. Gra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Feedback Vertex Set
In the mathematical discipline of graph theory, a feedback vertex set (FVS) of a graph is a set of vertices whose removal leaves a graph without cycles ("removal" means deleting the vertex and all edges adjacent to it). Equivalently, each FVS contains at least one vertex of any cycle in the graph. The feedback vertex set number of a graph is the size of a smallest FVS. Whether there exists a feedback vertex set of size at most k is an NP-complete problem; it was among the first problems shown to be NP-complete. It has wide applications in operating systems, database systems, and VLSI chip design. Definition The FVS decision problem is as follows: :INSTANCE: An (undirected or directed) graph G = (V, E) and a positive integer k. :QUESTION: Is there a subset X \subseteq V with , X, \leq k such that, when all vertices of X and their adjacent edges are deleted from G, the remainder is cycle-free? The graph G \setminus X/math> that remains after removing X from G is an induced ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |