topological sorting on:
[Wikipedia]
[Google]
[Amazon]
In
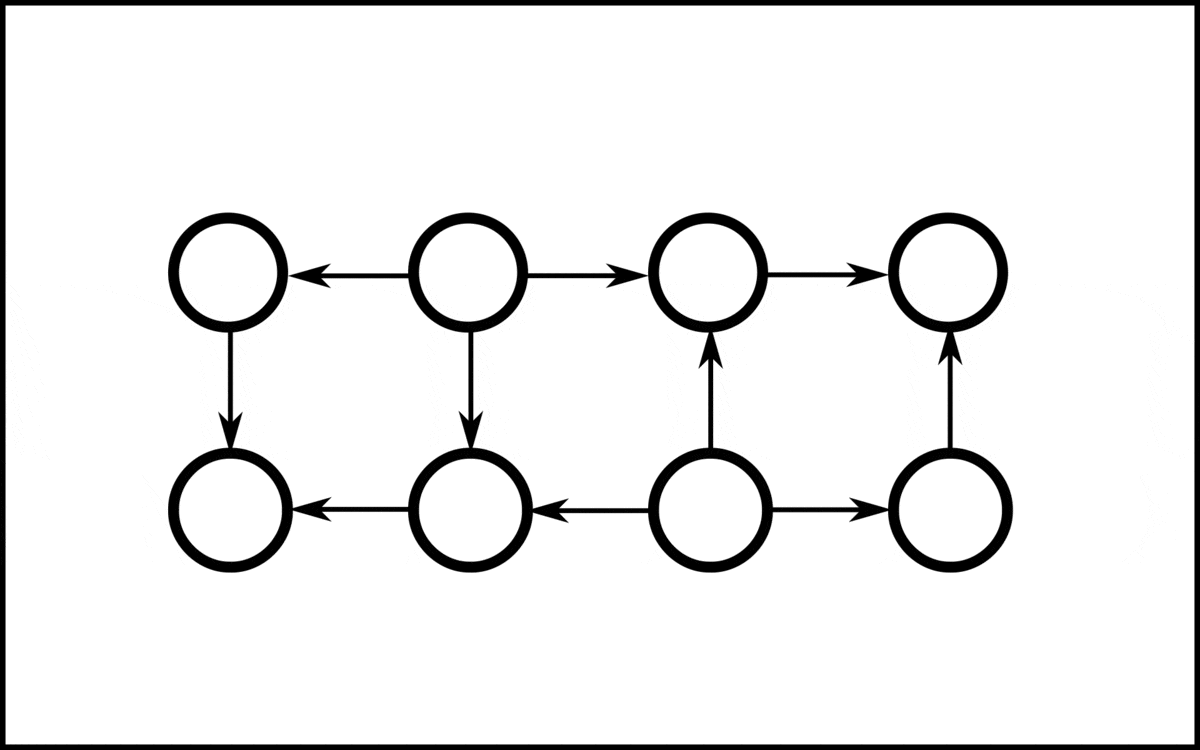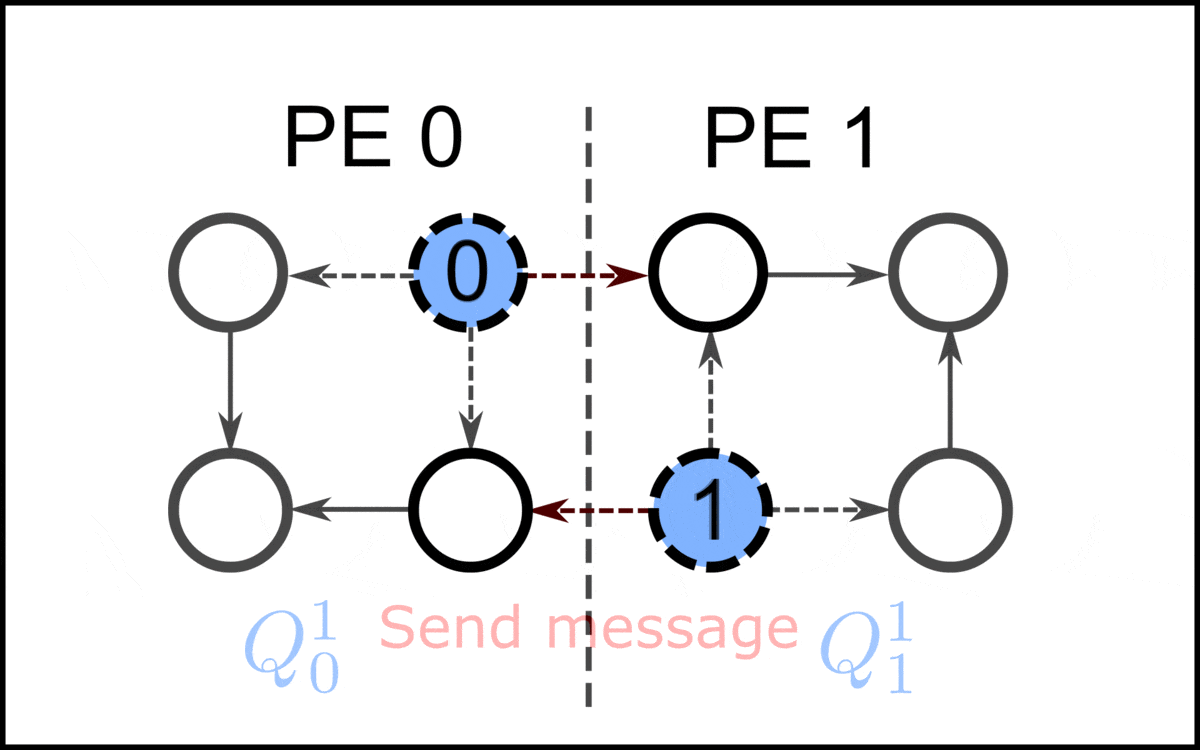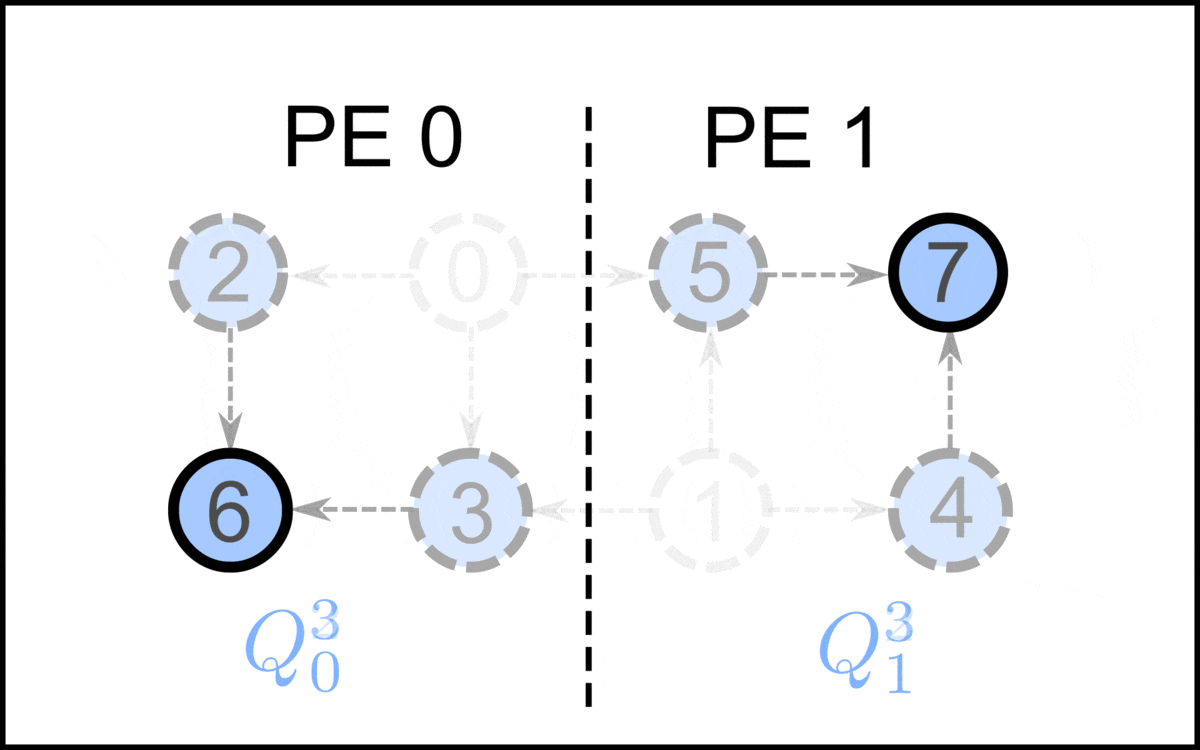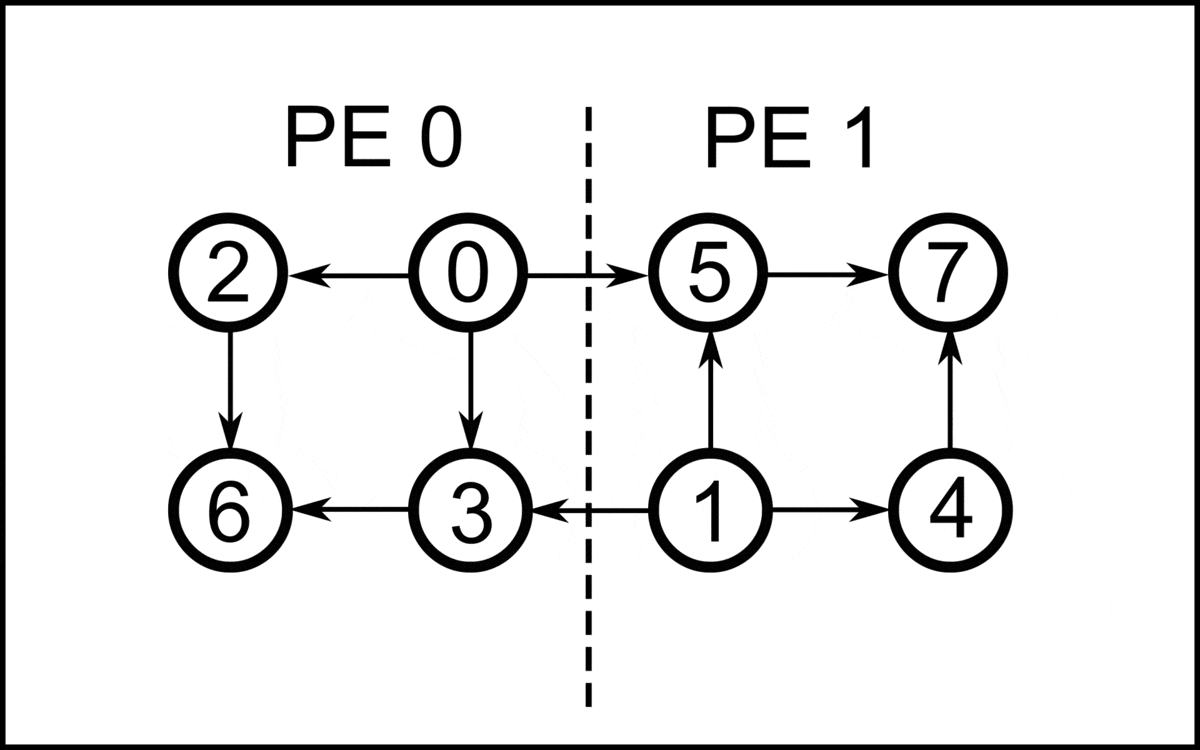 In the first step, PE assigns the indices to the local vertices in . These vertices in are removed, together with their corresponding outgoing edges. For each outgoing edge with endpoint in another PE , the message is posted to PE . After all vertices in are removed, the posted messages are sent to their corresponding PE. Each message received updates the indegree of the local vertex . If the indegree drops to zero, is added to . Then the next iteration starts.
In step , PE assigns the indices , where is the total number of processed vertices after step . This procedure repeats until there are no vertices left to process, hence . Below is a high level, single program, multiple data pseudo-code overview of this algorithm.
Note that the prefix sum for the local offsets can be efficiently calculated in parallel.
p processing elements with IDs from 0 to ''p''-1
Input: G = (V, E) DAG, distributed to PEs, PE index j = 0, ..., p - 1
Output: topological sorting of G
function traverseDAGDistributed
δ incoming degree of local vertices ''V''
// All vertices with indegree 0
nrOfVerticesProcessed = 0
do
global build prefix sum over size of ''Q'' // get offsets and total number of vertices in this step
offset = nrOfVerticesProcessed + sum(Qi, i = 0 to j - 1) // ''j'' is the processor index
foreach u in Q
localOrder = index++;
foreach (u,v) in E do post message (''u, v'') to PE owning vertex ''v''
nrOfVerticesProcessed += sum(, Qi, , i = 0 to p - 1)
deliver all messages to neighbors of vertices in Q
receive messages for local vertices V
remove all vertices in Q
foreach message (''u, v'') received:
if --δ = 0
add ''v'' to ''Q''
while global size of ''Q'' > 0
return localOrder
The communication cost depends heavily on the given graph partition. As for runtime, on a CRCW-PRAM model that allows fetch-and-decrement in constant time, this algorithm runs in , where is again the longest path in and the maximum degree.
In the first step, PE assigns the indices to the local vertices in . These vertices in are removed, together with their corresponding outgoing edges. For each outgoing edge with endpoint in another PE , the message is posted to PE . After all vertices in are removed, the posted messages are sent to their corresponding PE. Each message received updates the indegree of the local vertex . If the indegree drops to zero, is added to . Then the next iteration starts.
In step , PE assigns the indices , where is the total number of processed vertices after step . This procedure repeats until there are no vertices left to process, hence . Below is a high level, single program, multiple data pseudo-code overview of this algorithm.
Note that the prefix sum for the local offsets can be efficiently calculated in parallel.
p processing elements with IDs from 0 to ''p''-1
Input: G = (V, E) DAG, distributed to PEs, PE index j = 0, ..., p - 1
Output: topological sorting of G
function traverseDAGDistributed
δ incoming degree of local vertices ''V''
// All vertices with indegree 0
nrOfVerticesProcessed = 0
do
global build prefix sum over size of ''Q'' // get offsets and total number of vertices in this step
offset = nrOfVerticesProcessed + sum(Qi, i = 0 to j - 1) // ''j'' is the processor index
foreach u in Q
localOrder = index++;
foreach (u,v) in E do post message (''u, v'') to PE owning vertex ''v''
nrOfVerticesProcessed += sum(, Qi, , i = 0 to p - 1)
deliver all messages to neighbors of vertices in Q
receive messages for local vertices V
remove all vertices in Q
foreach message (''u, v'') received:
if --δ = 0
add ''v'' to ''Q''
while global size of ''Q'' > 0
return localOrder
The communication cost depends heavily on the given graph partition. As for runtime, on a CRCW-PRAM model that allows fetch-and-decrement in constant time, this algorithm runs in , where is again the longest path in and the maximum degree.
NIST Dictionary of Algorithms and Data Structures: topological sort
* {{sorting Graph algorithms Sorting algorithms Directed acyclic graphs Articles with example pseudocode
computer science
Computer science is the study of computation, information, and automation. Computer science spans Theoretical computer science, theoretical disciplines (such as algorithms, theory of computation, and information theory) to Applied science, ...
, a topological sort or topological ordering of a directed graph is a linear ordering of its vertices such that for every directed edge ''(u,v)'' from vertex ''u'' to vertex ''v'', ''u'' comes before ''v'' in the ordering. For instance, the vertices of the graph may represent tasks to be performed, and the edges may represent constraints that one task must be performed before another; in this application, a topological ordering is just a valid sequence for the tasks. Precisely, a topological sort is a graph traversal in which each node ''v'' is visited only after all its dependencies are visited''.'' A topological ordering is possible if and only if the graph has no directed cycles, that is, if it is a directed acyclic graph (DAG). Any DAG has at least one topological ordering, and there are linear time algorithm
In mathematics and computer science, an algorithm () is a finite sequence of Rigour#Mathematics, mathematically rigorous instructions, typically used to solve a class of specific Computational problem, problems or to perform a computation. Algo ...
s for constructing it. Topological sorting has many applications, especially in ranking problems such as feedback arc set. Topological sorting is also possible when the DAG has disconnected components.
Examples
The canonical application of topological sorting is in scheduling a sequence of jobs or tasks based on their dependencies. The jobs are represented by vertices, and there is an edge from ''x'' to ''y'' if job ''x'' must be completed before job ''y'' can be started (for example, when washing clothes, the washing machine must finish before we put the clothes in the dryer). Then, a topological sort gives an order in which to perform the jobs. A closely-related application of topological sorting algorithms was first studied in the early 1960s in the context of the PERT technique for scheduling inproject management
Project management is the process of supervising the work of a Project team, team to achieve all project goals within the given constraints. This information is usually described in project initiation documentation, project documentation, crea ...
. In this application, the vertices of a graph represent the milestones of a project, and the edges represent tasks that must be performed between one milestone and another. Topological sorting forms the basis of linear-time algorithms for finding the critical path of the project, a sequence of milestones and tasks that controls the length of the overall project schedule.
In computer science, applications of this type arise in instruction scheduling, ordering of formula cell evaluation when recomputing formula values in spreadsheet
A spreadsheet is a computer application for computation, organization, analysis and storage of data in tabular form. Spreadsheets were developed as computerized analogs of paper accounting worksheets. The program operates on data entered in c ...
s, logic synthesis, determining the order of compilation tasks to perform in makefile
In software development, Make is a command-line interface software tool that performs actions ordered by configured Dependence analysis, dependencies as defined in a configuration file called a ''makefile''. It is commonly used for build automati ...
s, data serialization
In computing, serialization (or serialisation, also referred to as pickling in Python (programming language), Python) is the process of translating a data structure or object (computer science), object state into a format that can be stored (e. ...
, and resolving symbol dependencies in linkers. It is also used to decide in which order to load tables with foreign keys in databases.
Algorithms
The usual algorithms for topological sorting have running time linear in the number of nodes plus the number of edges, asymptotically,Kahn's algorithm
One of these algorithms, first described by , works by choosing vertices in the same order as the eventual topological sort. First, find a list of "start nodes" that have no incoming edges and insert them into a set S; at least one such node must exist in a non-empty (finite) acyclic graph. Then: ''L'' ← Empty list that will contain the sorted elements ''S'' ← Set of all nodes with no incoming edge while ''S'' is not empty do remove a node ''n'' from ''S'' add ''n'' to ''L'' for each node ''m'' with an edge ''e'' from ''n'' to ''m'' do remove edge ''e'' from the graph if ''m'' has no other incoming edges then insert ''m'' into ''S'' if ''graph'' has edges then return error ''(graph has at least one cycle)'' else return ''L'' ''(a topologically sorted order)'' If the graph is a DAG, a solution will be contained in the list L (although the solution is not necessarily unique). Otherwise, the graph must have at least one cycle and therefore a topological sort is impossible. Reflecting the non-uniqueness of the resulting sort, the structure S can be simply a set or a queue or a stack. Depending on the order that nodes n are removed from set S, a different solution is created. A variation of Kahn's algorithm that breaks ties lexicographically forms a key component of the Coffman–Graham algorithm for parallel scheduling and layered graph drawing.Depth-first search
An alternative algorithm for topological sorting is based on depth-first search. The algorithm loops through each node of the graph, in an arbitrary order, initiating a depth-first search that terminates when it hits any node that has already been visited since the beginning of the topological sort or the node has no outgoing edges (i.e., a leaf node): ''L'' ← Empty list that will contain the sorted nodes while exists nodes without a permanent mark do select an unmarked node ''n'' visit(''n'') function visit(node ''n'') if ''n'' has a permanent mark then return if ''n'' has a temporary mark then stop ''(graph has at least one cycle)'' mark ''n'' with a temporary mark for each node ''m'' with an edge from ''n'' to ''m'' do visit(''m'') mark ''n'' with a permanent mark add ''n'' to head of ''L'' Each node ''n'' gets ''prepended'' to the output list L only after considering all other nodes that depend on ''n'' (all descendants of ''n'' in the graph). Specifically, when the algorithm adds node ''n'', we are guaranteed that all nodes that depend on ''n'' are already in the output list L: they were added to L either by the recursive call to visit() that ended before the call to visit ''n'', or by a call to visit() that started even before the call to visit ''n''. Since each edge and node is visited once, the algorithm runs in linear time. This depth-first-search-based algorithm is the one described by ; it seems to have been first described in print by Tarjan in 1976.Parallel algorithms
On a parallel random-access machine, a topological ordering can be constructed in ''O''((log ''n'')2) time using a polynomial number of processors, putting the problem into the complexity class NC2. One method for doing this is to repeatedly square the adjacency matrix of the given graph, logarithmically many times, using min-plus matrix multiplication with maximization in place of minimization. The resulting matrix describes the longest path distances in the graph. Sorting the vertices by the lengths of their longest incoming paths produces a topological ordering. An algorithm for parallel topological sorting on distributed memory machines parallelizes the algorithm of Kahn for a DAG . On a high level, the algorithm of Kahn repeatedly removes the vertices of indegree 0 and adds them to the topological sorting in the order in which they were removed. Since the outgoing edges of the removed vertices are also removed, there will be a new set of vertices of indegree 0, where the procedure is repeated until no vertices are left. This algorithm performs iterations, where is the longest path in . Each iteration can be parallelized, which is the idea of the following algorithm. In the following, it is assumed that the graph partition is stored on processing elements (PE), which are labeled . Each PE initializes a set of local vertices with indegree 0, where the upper index represents the current iteration. Since all vertices in the local sets have indegree 0, i.e., they are not adjacent, they can be given in an arbitrary order for a valid topological sorting. To assign a global index to each vertex, a prefix sum is calculated over the sizes of . So, each step, there are vertices added to the topological sorting. In the first step, PE assigns the indices to the local vertices in . These vertices in are removed, together with their corresponding outgoing edges. For each outgoing edge with endpoint in another PE , the message is posted to PE . After all vertices in are removed, the posted messages are sent to their corresponding PE. Each message received updates the indegree of the local vertex . If the indegree drops to zero, is added to . Then the next iteration starts.
In step , PE assigns the indices , where is the total number of processed vertices after step . This procedure repeats until there are no vertices left to process, hence . Below is a high level, single program, multiple data pseudo-code overview of this algorithm.
Note that the prefix sum for the local offsets can be efficiently calculated in parallel.
p processing elements with IDs from 0 to ''p''-1
Input: G = (V, E) DAG, distributed to PEs, PE index j = 0, ..., p - 1
Output: topological sorting of G
function traverseDAGDistributed
δ incoming degree of local vertices ''V''
// All vertices with indegree 0
nrOfVerticesProcessed = 0
do
global build prefix sum over size of ''Q'' // get offsets and total number of vertices in this step
offset = nrOfVerticesProcessed + sum(Qi, i = 0 to j - 1) // ''j'' is the processor index
foreach u in Q
localOrder = index++;
foreach (u,v) in E do post message (''u, v'') to PE owning vertex ''v''
nrOfVerticesProcessed += sum(, Qi, , i = 0 to p - 1)
deliver all messages to neighbors of vertices in Q
receive messages for local vertices V
remove all vertices in Q
foreach message (''u, v'') received:
if --δ = 0
add ''v'' to ''Q''
while global size of ''Q'' > 0
return localOrder
The communication cost depends heavily on the given graph partition. As for runtime, on a CRCW-PRAM model that allows fetch-and-decrement in constant time, this algorithm runs in , where is again the longest path in and the maximum degree.
In the first step, PE assigns the indices to the local vertices in . These vertices in are removed, together with their corresponding outgoing edges. For each outgoing edge with endpoint in another PE , the message is posted to PE . After all vertices in are removed, the posted messages are sent to their corresponding PE. Each message received updates the indegree of the local vertex . If the indegree drops to zero, is added to . Then the next iteration starts.
In step , PE assigns the indices , where is the total number of processed vertices after step . This procedure repeats until there are no vertices left to process, hence . Below is a high level, single program, multiple data pseudo-code overview of this algorithm.
Note that the prefix sum for the local offsets can be efficiently calculated in parallel.
p processing elements with IDs from 0 to ''p''-1
Input: G = (V, E) DAG, distributed to PEs, PE index j = 0, ..., p - 1
Output: topological sorting of G
function traverseDAGDistributed
δ incoming degree of local vertices ''V''
// All vertices with indegree 0
nrOfVerticesProcessed = 0
do
global build prefix sum over size of ''Q'' // get offsets and total number of vertices in this step
offset = nrOfVerticesProcessed + sum(Qi, i = 0 to j - 1) // ''j'' is the processor index
foreach u in Q
localOrder = index++;
foreach (u,v) in E do post message (''u, v'') to PE owning vertex ''v''
nrOfVerticesProcessed += sum(, Qi, , i = 0 to p - 1)
deliver all messages to neighbors of vertices in Q
receive messages for local vertices V
remove all vertices in Q
foreach message (''u, v'') received:
if --δ = 0
add ''v'' to ''Q''
while global size of ''Q'' > 0
return localOrder
The communication cost depends heavily on the given graph partition. As for runtime, on a CRCW-PRAM model that allows fetch-and-decrement in constant time, this algorithm runs in , where is again the longest path in and the maximum degree.
Application to shortest path finding
The topological ordering can also be used to quickly computeshortest paths
In graph theory, the shortest path problem is the problem of finding a path between two vertices (or nodes) in a graph such that the sum of the weights of its constituent edges is minimized.
The problem of finding the shortest path between t ...
through a weighted directed acyclic graph. Let be the list of vertices in such a graph, in topological order. Then the following algorithm computes the shortest path from some source vertex to all other vertices:
* Let be an array of the same length as ; this will hold the shortest-path distances from . Set , all other .
* Let be an array of the same length as , with all elements initialized to . Each will hold the predecessor of in the shortest path from to .
* Loop over the vertices as ordered in , starting from :
** For each vertex directly following (i.e., there exists an edge from to ):
*** Let be the weight of the edge from to .
*** Relax the edge: if , set
**** ,
**** .
Equivalently:
* Let be an array of the same length as ; this will hold the shortest-path distances from . Set , all other .
* Let be an array of the same length as , with all elements initialized to . Each will hold the predecessor of in the shortest path from to .
* Loop over the vertices as ordered in , starting from :
** For each vertex into (i.e., there exists an edge from to ):
*** Let be the weight of the edge from to .
*** Relax the edge: if , set
**** ,
**** .
On a graph of vertices and edges, this algorithm takes , i.e., linear
In mathematics, the term ''linear'' is used in two distinct senses for two different properties:
* linearity of a '' function'' (or '' mapping'');
* linearity of a '' polynomial''.
An example of a linear function is the function defined by f(x) ...
, time.
Uniqueness
If a topological sort has the property that all pairs of consecutive vertices in the sorted order are connected by edges, then these edges form a directed Hamiltonian path in the DAG. If a Hamiltonian path exists, the topological sort order is unique; no other order respects the edges of the path. Conversely, if a topological sort does not form a Hamiltonian path, the DAG will have two or more valid topological orderings, for in this case it is always possible to form a second valid ordering by swapping two consecutive vertices that are not connected by an edge to each other. Therefore, it is possible to test in linear time whether a unique ordering exists, and whether a Hamiltonian path exists, despite theNP-hard
In computational complexity theory, a computational problem ''H'' is called NP-hard if, for every problem ''L'' which can be solved in non-deterministic polynomial-time, there is a polynomial-time reduction from ''L'' to ''H''. That is, assumi ...
ness of the Hamiltonian path problem for more general directed graphs (i.e., cyclic directed graphs).
Relation to partial orders
Topological orderings are also closely related to the concept of a linear extension of apartial order
In mathematics, especially order theory, a partial order on a set is an arrangement such that, for certain pairs of elements, one precedes the other. The word ''partial'' is used to indicate that not every pair of elements needs to be comparable ...
in mathematics. A partially ordered set is just a set of objects together with a definition of the "≤" inequality relation, satisfying the axioms of reflexivity (''x'' ≤ ''x''), antisymmetry (if ''x'' ≤ ''y'' and ''y'' ≤ ''x'' then ''x'' = ''y'') and transitivity (if ''x'' ≤ ''y'' and ''y'' ≤ ''z'', then ''x'' ≤ ''z''). A total order
In mathematics, a total order or linear order is a partial order in which any two elements are comparable. That is, a total order is a binary relation \leq on some set X, which satisfies the following for all a, b and c in X:
# a \leq a ( re ...
is a partial order in which, for every two objects ''x'' and ''y'' in the set, either ''x'' ≤ ''y'' or ''y'' ≤ ''x''. Total orders are familiar in computer science as the comparison operators needed to perform comparison sorting algorithms. For finite sets, total orders may be identified with linear sequences of objects, where the "≤" relation is true whenever the first object precedes the second object in the order; a comparison sorting algorithm may be used to convert a total order into a sequence in this way. A linear extension of a partial order is a total order that is compatible with it, in the sense that, if ''x'' ≤ ''y'' in the partial order, then ''x'' ≤ ''y'' in the total order as well.
One can define a partial ordering from any DAG by letting the set of objects be the vertices of the DAG, and defining ''x'' ≤ ''y'' to be true, for any two vertices ''x'' and ''y'', whenever there exists a directed path from ''x'' to ''y''; that is, whenever ''y'' is reachable from ''x''. With these definitions, a topological ordering of the DAG is the same thing as a linear extension of this partial order. Conversely, any partial ordering may be defined as the reachability relation in a DAG. One way of doing this is to define a DAG that has a vertex for every object in the partially ordered set, and an edge ''xy'' for every pair of objects for which ''x'' ≤ ''y''. An alternative way of doing this is to use the transitive reduction of the partial ordering; in general, this produces DAGs with fewer edges, but the reachability relation in these DAGs is still the same partial order. By using these constructions, one can use topological ordering algorithms to find linear extensions of partial orders.
Relation to scheduling optimisation
By definition, the solution of a scheduling problem that includes a precedence graph is a valid solution to topological sort (irrespective of the number of machines), however, topological sort in itself is ''not'' enough to optimally solve a scheduling optimisation problem. Hu's algorithm is a popular method used to solve scheduling problems that require a precedence graph and involve processing times (where the goal is to minimise the largest completion time amongst all the jobs). Like topological sort, Hu's algorithm is not unique and can be solved using DFS (by finding the largest path length and then assigning the jobs).See also
* tsort, a Unix program for topological sorting * Feedback arc set, a set of edges whose removal allows the remaining subgraph to be topologically sorted * Tarjan's strongly connected components algorithm, an algorithm that gives the topologically sorted list of strongly connected components in a graph * Pre-topological orderReferences
Further reading
* D. E. Knuth, The Art of Computer Programming, Volume 1, section 2.2.3, which gives an algorithm for topological sorting of a partial ordering, and a brief history. *Bertrand Meyer
Bertrand Meyer (; ; born 21 November 1950) is a French academic, author, and consultant in the field of computer languages. He created the Eiffel programming language and the concept of design by contract.
Education and academic career
Meyer ...
, ''Touch of Class: Learning to Program Well with Objects and Contracts'', Springer
Springer or springers may refer to:
Publishers
* Springer Science+Business Media, aka Springer International Publishing, a worldwide publishing group founded in 1842 in Germany formerly known as Springer-Verlag.
** Springer Nature, a multinationa ...
, 2009, chapter 15, ''Devising and engineering an algorithm: topological sort'', using a modern programming language, for a detailed pedagogical presentation of topological sort (using a variant of Kahn's algorithm) with consideration of data structure design, API design, and software engineering concerns.
External links
NIST Dictionary of Algorithms and Data Structures: topological sort
* {{sorting Graph algorithms Sorting algorithms Directed acyclic graphs Articles with example pseudocode