|
Fano Factor
In statistics, the Fano factor, like the coefficient of variation, is a measure of the dispersion of a probability distribution of a Fano noise. It is named after Ugo Fano, an Italian American physicist. The Fano factor is defined as :F=\frac, where \sigma_W^2 is the variance and \mu_W is the mean of a random process in some time window ''W''. The Fano factor can be viewed as a kind of noise-to-signal ratio; it is a measure of the reliability with which the random variable could be estimated from a time window that on average contains several random events. For a Poisson process, the variance in the count equals the mean count, so ''F'' = 1 (normalization). If the time window is chosen to be infinity, the Fano factor is similar to the variance-to-mean ratio (VMR) which in statistics is also known as the index of dispersion. Use in particle detection In particle detectors, the Fano factor results from the energy loss in a collision not being purely statistical. Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German: '' Statistik'', "description of a state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of surveys and experiments.Dodge, Y. (2006) ''The Oxford Dictionary of Statistical Terms'', Oxford University Press. When census data cannot be collected, statisticians collect data by developing specific experiment designs and survey samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample to the population as a whole. An ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Poisson Process
In probability, statistics and related fields, a Poisson point process is a type of random mathematical object that consists of points randomly located on a mathematical space with the essential feature that the points occur independently of one another. The Poisson point process is often called simply the Poisson process, but it is also called a Poisson random measure, Poisson random point field or Poisson point field. This point process has convenient mathematical properties, which has led to its being frequently defined in Euclidean space and used as a mathematical model for seemingly random processes in numerous disciplines such as astronomy,G. J. Babu and E. D. Feigelson. Spatial point processes in astronomy. ''Journal of statistical planning and inference'', 50(3):311–326, 1996. biology,H. G. Othmer, S. R. Dunbar, and W. Alt. Models of dispersal in biological systems. ''Journal of mathematical biology'', 26(3):263–298, 1988. ecology,H. Thompson. Spatial point processes, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Index Of Dispersion
In probability theory and statistics, the index of dispersion, dispersion index, coefficient of dispersion, relative variance, or variance-to-mean ratio (VMR), like the coefficient of variation, is a normalized measure of the dispersion of a probability distribution: it is a measure used to quantify whether a set of observed occurrences are clustered or dispersed compared to a standard statistical model. It is defined as the ratio of the variance \sigma^2 to the mean \mu,'' :D = . It is also known as the Fano factor, though this term is sometimes reserved for ''windowed'' data (the mean and variance are computed over a subpopulation), where the index of dispersion is used in the special case where the window is infinite. Windowing data is frequently done: the VMR is frequently computed over various intervals in time or small regions in space, which may be called "windows", and the resulting statistic called the Fano factor. It is only defined when the mean \mu is non-zero, a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Neuroscience
Neuroscience is the science, scientific study of the nervous system (the brain, spinal cord, and peripheral nervous system), its functions and disorders. It is a Multidisciplinary approach, multidisciplinary science that combines physiology, anatomy, molecular biology, developmental biology, cytology, psychology, physics, computer science, chemistry, medicine, statistics, and Mathematical Modeling, mathematical modeling to understand the fundamental and emergent properties of neurons, glia and neural circuits. The understanding of the biological basis of learning, memory, behavior, perception, and consciousness has been described by Eric Kandel as the "epic challenge" of the Biology, biological sciences. The scope of neuroscience has broadened over time to include different approaches used to study the nervous system at different scales. The techniques used by neuroscientists have expanded enormously, from molecular biology, molecular and cell biology, cellular studies of indivi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cadmium Zinc Telluride
Cadmium zinc telluride, (CdZnTe) or CZT, is a compound of cadmium, zinc and tellurium or, more strictly speaking, an alloy of cadmium telluride and zinc telluride. A direct bandgap semiconductor, it is used in a variety of applications, including semiconductor radiation detectors, photorefractive gratings, electro-optic modulators, solar cells, and terahertz generation and detection. The band gap varies from approximately 1.4 to 2.2 eV, depending on composition. Radiation detectors using CZT can operate in direct-conversion (or photoconductive) mode at room temperature, unlike some other materials (particularly germanium) which require cooling. Their relative advantages include high sensitivity for X-rays and gamma rays, due to the high atomic numbers of Cd and Te, and better energy resolution than scintillator detectors A scintillator is a material that exhibits scintillation, the property of luminescence, when excited by ionizing radiation. Luminescent materials, when ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Full Width At Half Maximum
In a distribution, full width at half maximum (FWHM) is the difference between the two values of the independent variable at which the dependent variable is equal to half of its maximum value. In other words, it is the width of a spectrum curve measured between those points on the ''y''-axis which are half the maximum amplitude. Half width at half maximum (HWHM) is half of the FWHM if the function is symmetric. The term full duration at half maximum (FDHM) is preferred when the independent variable is time. FWHM is applied to such phenomena as the duration of pulse (signal processing), pulse waveforms and the spectral width of sources used for optical telecommunication, communications and the resolution of spectrometers. The convention of "width" meaning "half maximum" is also widely used in signal processing to define bandwidth (signal processing), bandwidth as "width of frequency range where less than half the signal's power is attenuated", i.e., the power is at least half the max ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
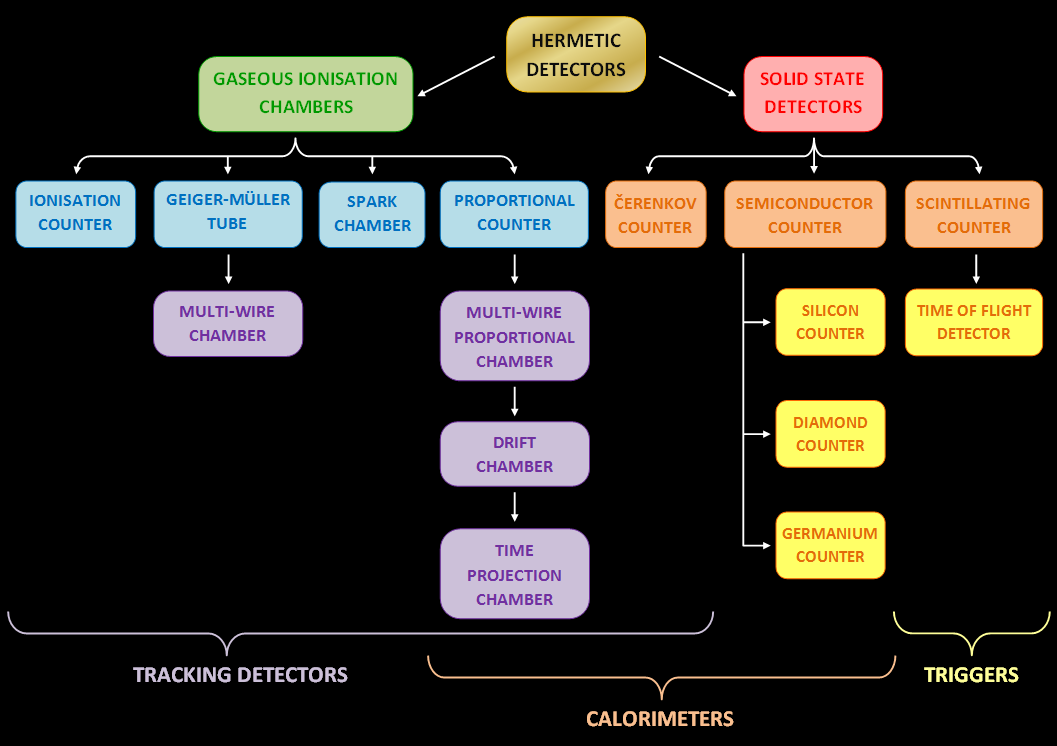
Particle Detector
In experimental and applied particle physics, nuclear physics, and nuclear engineering, a particle detector, also known as a radiation detector, is a device used to detect, track, and/or identify ionizing particles, such as those produced by nuclear decay, cosmic radiation, or reactions in a particle accelerator. Detectors can measure the particle energy and other attributes such as momentum, spin, charge, particle type, in addition to merely registering the presence of the particle. Examples and types Many of the detectors invented and used so far are ionization detectors (of which gaseous ionization detectors and semiconductor detectors are most typical) and scintillation detectors; but other, completely different principles have also been applied, like Čerenkov light and transition radiation. Historical examples * Bubble chamber * Wilson cloud chamber (diffusion chamber) *Photographic plate ;Detectors for radiation protection The following types of particle detec ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Index Of Dispersion
In probability theory and statistics, the index of dispersion, dispersion index, coefficient of dispersion, relative variance, or variance-to-mean ratio (VMR), like the coefficient of variation, is a normalized measure of the dispersion of a probability distribution: it is a measure used to quantify whether a set of observed occurrences are clustered or dispersed compared to a standard statistical model. It is defined as the ratio of the variance \sigma^2 to the mean \mu,'' :D = . It is also known as the Fano factor, though this term is sometimes reserved for ''windowed'' data (the mean and variance are computed over a subpopulation), where the index of dispersion is used in the special case where the window is infinite. Windowing data is frequently done: the VMR is frequently computed over various intervals in time or small regions in space, which may be called "windows", and the resulting statistic called the Fano factor. It is only defined when the mean \mu is non-zero, a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Variance-to-mean Ratio
In probability theory and statistics, the index of dispersion, dispersion index, coefficient of dispersion, relative variance, or variance-to-mean ratio (VMR), like the coefficient of variation, is a normalized measure of the dispersion of a probability distribution: it is a measure used to quantify whether a set of observed occurrences are clustered or dispersed compared to a standard statistical model. It is defined as the ratio of the variance \sigma^2 to the mean \mu,'' :D = . It is also known as the Fano factor, though this term is sometimes reserved for ''windowed'' data (the mean and variance are computed over a subpopulation), where the index of dispersion is used in the special case where the window is infinite. Windowing data is frequently done: the VMR is frequently computed over various intervals in time or small regions in space, which may be called "windows", and the resulting statistic called the Fano factor. It is only defined when the mean \mu is non-zero, and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Random Event
In probability theory, an event is a set of outcomes of an experiment (a subset of the sample space) to which a probability is assigned. A single outcome may be an element of many different events, and different events in an experiment are usually not equally likely, since they may include very different groups of outcomes. An event consisting of only a single outcome is called an or an ; that is, it is a singleton set. An event S is said to if S contains the outcome x of the experiment (or trial) (that is, if x \in S). The probability (with respect to some probability measure) that an event S occurs is the probability that S contains the outcome x of an experiment (that is, it is the probability that x \in S). An event defines a complementary event, namely the complementary set (the event occurring), and together these define a Bernoulli trial: did the event occur or not? Typically, when the sample space is finite, any subset of the sample space is an event (that is, all e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coefficient Of Variation
In probability theory and statistics, the coefficient of variation (CV), also known as relative standard deviation (RSD), is a standardized measure of dispersion of a probability distribution or frequency distribution. It is often expressed as a percentage, and is defined as the ratio of the standard deviation \sigma to the mean \mu (or its absolute value, The CV or RSD is widely used in analytical chemistry to express the precision and repeatability of an assay. It is also commonly used in fields such as engineering or physics when doing quality assurance studies and ANOVA gauge R&R, by economists and investors in economic models, and in neuroscience. Definition The coefficient of variation (CV) is defined as the ratio of the standard deviation \ \sigma to the mean \ \mu , c_ = \frac. It shows the extent of variability in relation to the mean of the population. The coefficient of variation should be computed only for data measured on scales that have a meaningfu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Random Variable
A random variable (also called random quantity, aleatory variable, or stochastic variable) is a mathematical formalization of a quantity or object which depends on random events. It is a mapping or a function from possible outcomes (e.g., the possible upper sides of a flipped coin such as heads H and tails T) in a sample space (e.g., the set \) to a measurable space, often the real numbers (e.g., \ in which 1 corresponding to H and -1 corresponding to T). Informally, randomness typically represents some fundamental element of chance, such as in the roll of a dice; it may also represent uncertainty, such as measurement error. However, the interpretation of probability is philosophically complicated, and even in specific cases is not always straightforward. The purely mathematical analysis of random variables is independent of such interpretational difficulties, and can be based upon a rigorous axiomatic setup. In the formal mathematical language of measure theory, a rando ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |