|
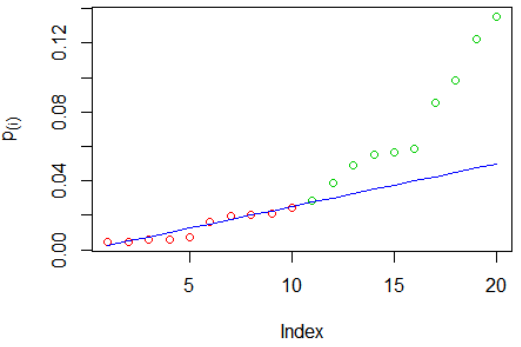
False Coverage Rate
In statistics, a false coverage rate (FCR) is the average rate of false coverage, i.e. not covering the true parameters, among the selected intervals. The FCR gives a simultaneous coverage at a (1 − ''α'')×100% level for all of the parameters considered in the problem. The FCR has a strong connection to the false discovery rate (FDR). Both methods address the problem of multiple comparisons, FCR from confidence intervals (CIs) and FDR from P-value's point of view. FCR was needed because of dangers caused by selective inference. Researchers and scientists tend to report or highlight only the portion of data that is considered significant without clearly indicating the various hypothesis that were considered. It is therefore necessary to understand how the data is falsely covered. There are many FCR procedures which can be used depending on the length of the CI – Bonferroni-selected–Bonferroni-adjusted, Adjusted BH-Selected CIs (Benjamini and Yekutieli ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German language, German: ', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of statistical survey, surveys and experimental design, experiments. When census data (comprising every member of the target population) cannot be collected, statisticians collect data by developing specific experiment designs and survey sample (statistics), samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coverage (statistics)
In statistical estimation theory, the coverage probability, or coverage for short, is the probability that a confidence interval or confidence region will include the true value (parameter) of interest. It can be defined as the proportion of instances where the interval surrounds the true value as assessed by long-run frequency. In statistical prediction, the coverage probability is the probability that a prediction interval will include an out-of-sample value of the random variable. The coverage probability can be defined as the proportion of instances where the interval surrounds an out-of-sample value as assessed by long-run frequency. Concept The fixed degree of certainty pre-specified by the analyst, referred to as the ''confidence level'' or ''confidence coefficient'' of the constructed interval, is effectively the nominal coverage probability of the procedure for constructing confidence intervals. Hence, referring to a "nominal confidence level" or "nominal confid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
False Discovery Rate
In statistics, the false discovery rate (FDR) is a method of conceptualizing the rate of type I errors in null hypothesis testing when conducting multiple comparisons. FDR-controlling procedures are designed to control the FDR, which is the expected proportion of "discoveries" (rejected null hypotheses) that are false (incorrect rejections of the null). Equivalently, the FDR is the expected ratio of the number of false positive classifications (false discoveries) to the total number of positive classifications (rejections of the null). The total number of rejections of the null include both the number of false positives (FP) and true positives (TP). Simply put, FDR = FP / (FP + TP). FDR-controlling procedures provide less stringent control of Type I errors compared to family-wise error rate (FWER) controlling procedures (such as the Bonferroni correction), which control the probability of ''at least one'' Type I error. Thus, FDR-controlling procedures have greater power, at t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Problem Of Multiple Comparisons
Multiple comparisons, multiplicity or multiple testing problem occurs in statistics when one considers a set of statistical inferences simultaneously or estimates a subset of parameters selected based on the observed values. The larger the number of inferences made, the more likely erroneous inferences become. Several statistical techniques have been developed to address this problem, for example, by requiring a stricter significance threshold for individual comparisons, so as to compensate for the number of inferences being made. Methods for family-wise error rate give the probability of false positives resulting from the multiple comparisons problem. History The problem of multiple comparisons received increased attention in the 1950s with the work of statisticians such as Tukey and Scheffé. Over the ensuing decades, many procedures were developed to address the problem. In 1996, the first international conference on multiple comparison procedures took place in Tel Aviv. Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Microarray
A microarray is a multiplex (assay), multiplex lab-on-a-chip. Its purpose is to simultaneously detect the expression of thousands of biological interactions. It is a two-dimensional array on a Substrate (materials science), solid substrate—usually a glass slide or silicon thin-film cell—that assays (tests) large amounts of biotic material, biological material using high-throughput screening miniaturized, multiplexed and parallel processing and detection methods. The concept and methodology of microarrays was first introduced and illustrated in antibody microarrays (also referred to as antibody matrix) by Tse Wen Chang in 1983 in a scientific publication and a series of patents. The "gene chip" industry started to grow significantly after the 1995 ''Science Magazine'' article by the Ron Davis and Pat Brown labs at Stanford University. With the establishment of companies, such as Affymetrix, Agilent, Applied Microarrays, Arrayjet, Illumina (company), Illumina, and others, the te ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Parameter
In statistics, as opposed to its general use in mathematics, a parameter is any quantity of a statistical population that summarizes or describes an aspect of the population, such as a mean or a standard deviation. If a population exactly follows a known and defined distribution, for example the normal distribution, then a small set of parameters can be measured which provide a comprehensive description of the population and can be considered to define a probability distribution for the purposes of extracting samples from this population. A "parameter" is to a population as a "statistic" is to a sample; that is to say, a parameter describes the true value calculated from the full population (such as the population mean), whereas a statistic is an estimated measurement of the parameter based on a sample (such as the sample mean, which is the mean of gathered data per sampling, called sample). Thus a "statistical parameter" can be more specifically referred to as a population ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Daniel Yekutieli
Daniel Yekutieli is an Israeli statistician and professor at Tel Aviv University. He is one of the leading researchers in the field of applied statistics in Israel. He is known for the creation of the false coverage rate and for his work on the false discovery rate with Yoav Benjamini, including the Benjamini–Yekutieli (BY) procedure for controlling it. Biography Yekutieli was born in Rehovot, Israel. His father, Gideon Yekutieli, was the first nuclear physicist in Israel and a professor at the Weizmann Institute of Science. His paternal grandfather was the founder of the Maccabiah Games, Yosef Yekutieli. His great-grandfather was Akiva Aryeh Weiss, one of the founders of '' Ahuzat Bayit'' (modern-day Tel Aviv). Yekutieli received his BA in Mathematics from the Hebrew University of Jerusalem in 1992, and went on to earn his MA and PhD in Applied Statistics from Tel Aviv University. His PhD thesis, supervised by Yoav Benjamini and completed in 2002, first introduced the conc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Classification Of Multiple Hypothesis Tests
Multiple comparisons, multiplicity or multiple testing problem occurs in statistics when one considers a set of statistical inferences simultaneously or estimates a subset of parameters selected based on the observed values. The larger the number of inferences made, the more likely erroneous inferences become. Several statistical techniques have been developed to address this problem, for example, by requiring a stricter significance threshold for individual comparisons, so as to compensate for the number of inferences being made. Methods for family-wise error rate give the probability of false positives resulting from the multiple comparisons problem. History The problem of multiple comparisons received increased attention in the 1950s with the work of statisticians such as Tukey and Scheffé. Over the ensuing decades, many procedures were developed to address the problem. In 1996, the first international conference on multiple comparison procedures took place in Tel Aviv. Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Selection Bias
Selection bias is the bias introduced by the selection of individuals, groups, or data for analysis in such a way that proper randomization is not achieved, thereby failing to ensure that the sample obtained is representative of the population intended to be analyzed. It is sometimes referred to as the selection effect. The phrase "selection bias" most often refers to the distortion of a statistical analysis, resulting from the method of collecting samples. If the selection bias is not taken into account, then some conclusions of the study may be false. Types of bias Sampling bias Sampling bias is systematic error due to a non-random sample of a population, causing some members of the population to be less likely to be included than others, resulting in a biased sample, defined as a statistical sample of a statistical population, population (or non-human factors) in which all participants are not equally balanced or objectively represented. It is mostly classified as a subtype of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
P-values
In null-hypothesis significance testing, the ''p''-value is the probability of obtaining test results at least as extreme as the result actually observed, under the assumption that the null hypothesis is correct. A very small ''p''-value means that such an extreme observed outcome would be very unlikely ''under the null hypothesis''. Even though reporting ''p''-values of statistical tests is common practice in academic publications of many quantitative fields, misinterpretation and misuse of p-values is widespread and has been a major topic in mathematics and metascience. In 2016, the American Statistical Association (ASA) made a formal statement that "''p''-values do not measure the probability that the studied hypothesis is true, or the probability that the data were produced by random chance alone" and that "a ''p''-value, or statistical significance, does not measure the size of an effect or the importance of a result" or "evidence regarding a model or hypothesis". That ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conditional Probability
In probability theory, conditional probability is a measure of the probability of an Event (probability theory), event occurring, given that another event (by assumption, presumption, assertion or evidence) is already known to have occurred. This particular method relies on event A occurring with some sort of relationship with another event B. In this situation, the event A can be analyzed by a conditional probability with respect to B. If the event of interest is and the event is known or assumed to have occurred, "the conditional probability of given ", or "the probability of under the condition ", is usually written as or occasionally . This can also be understood as the fraction of probability B that intersects with A, or the ratio of the probabilities of both events happening to the "given" one happening (how many times A occurs rather than not assuming B has occurred): P(A \mid B) = \frac. For example, the probability that any given person has a cough on any given day ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |