|
Conditional Probability
In probability theory, conditional probability is a measure of the probability of an Event (probability theory), event occurring, given that another event (by assumption, presumption, assertion or evidence) is already known to have occurred. This particular method relies on event A occurring with some sort of relationship with another event B. In this situation, the event A can be analyzed by a conditional probability with respect to B. If the event of interest is and the event is known or assumed to have occurred, "the conditional probability of given ", or "the probability of under the condition ", is usually written as or occasionally . This can also be understood as the fraction of probability B that intersects with A, or the ratio of the probabilities of both events happening to the "given" one happening (how many times A occurs rather than not assuming B has occurred): P(A \mid B) = \frac. For example, the probability that any given person has a cough on any given day ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Theory
Probability theory or probability calculus is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expressing it through a set of axioms of probability, axioms. Typically these axioms formalise probability in terms of a probability space, which assigns a measure (mathematics), measure taking values between 0 and 1, termed the probability measure, to a set of outcomes called the sample space. Any specified subset of the sample space is called an event (probability theory), event. Central subjects in probability theory include discrete and continuous random variables, probability distributions, and stochastic processes (which provide mathematical abstractions of determinism, non-deterministic or uncertain processes or measured Quantity, quantities that may either be single occurrences or evolve over time in a random fashion). Although it is no ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bruno De Finetti
Bruno de Finetti (13 June 1906 – 20 July 1985) was an Italian probabilist statistician and actuary, noted for the "operational subjective" conception of probability. The classic exposition of his distinctive theory is the 1937 , which discussed probability founded on the coherence of betting odds and the consequences of exchangeability. Life De Finetti was born in Innsbruck, Austria, and studied mathematics at Politecnico di Milano. He graduated in 1927, writing his thesis under the supervision of Giulio Vivanti. After graduation, he worked as an actuary and a statistician at ( National Institute of Statistics) in Rome and, from 1931, the Trieste insurance company Assicurazioni Generali. In 1936 he won a competition for Chair of Financial Mathematics and Statistics, but was not nominated due to a fascist law barring access to unmarried candidates; he was appointed as ordinary professor at the University of Trieste only in 1950. He published extensively (17 papers in 193 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radical Probabilism
Radical probabilism is a hypothesis in philosophy, in particular epistemology, and probability theory that holds that no facts are known for certain. That view holds profound implications for statistical inference. The philosophy is particularly associated with Richard Jeffrey who wittily characterised it with the ''dictum'' "It's probabilities all the way down." Background Bayes' theorem states a rule for updating a probability conditioned on other information. In 1967, Ian Hacking argued that in a static form, Bayes' theorem only connects probabilities that are held simultaneously; it does not tell the learner how to update probabilities when new evidence becomes available over time, contrary to what contemporary Bayesians suggested. According to Hacking, adopting Bayes' theorem is a temptation. Suppose that a learner forms probabilities ''P''old(''A'' & ''B'') = ''p'' and ''P''old(''B'') = ''q''. If the learner subsequently learns that ''B'' is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conditional Expectation
In probability theory, the conditional expectation, conditional expected value, or conditional mean of a random variable is its expected value evaluated with respect to the conditional probability distribution. If the random variable can take on only a finite number of values, the "conditions" are that the variable can only take on a subset of those values. More formally, in the case when the random variable is defined over a discrete probability space, the "conditions" are a partition of a set, partition of this probability space. Depending on the context, the conditional expectation can be either a random variable or a function. The random variable is denoted E(X\mid Y) analogously to conditional probability. The function form is either denoted E(X\mid Y=y) or a separate function symbol such as f(y) is introduced with the meaning E(X\mid Y) = f(Y). Examples Example 1: Dice rolling Consider the roll of a fair die and let ''A'' = 1 if the number is even (i.e., 2, 4, or 6) and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Law Of Total Probability
In probability theory, the law (or formula) of total probability is a fundamental rule relating marginal probabilities to conditional probabilities. It expresses the total probability of an outcome which can be realized via several distinct events, hence the name. Statement The law of total probability isZwillinger, D., Kokoska, S. (2000) ''CRC Standard Probability and Statistics Tables and Formulae'', CRC Press. page 31. a theorem that states, in its discrete case, if \left\ is a finite or countably infinite set of mutually exclusive and collectively exhaustive events, then for any event A :P(A)=\sum_n P(A\cap B_n) or, alternatively, :P(A)=\sum_n P(A\mid B_n)P(B_n), where, for any n, if P(B_n) = 0 , then these terms are simply omitted from the summation since P(A\mid B_n) is finite. The summation can be interpreted as a weighted average, and consequently the marginal probability, P(A), is sometimes called "average probability"; "overall probability" is sometimes used i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Borel–Kolmogorov Paradox
In probability theory, the Borel–Kolmogorov paradox (sometimes known as Borel's paradox) is a paradox relating to conditional probability with respect to an event of probability zero (also known as a null set). It is named after Émile Borel and Andrey Kolmogorov. A great circle puzzle Suppose that a random variable has a uniform distribution on a unit sphere. What is its conditional distribution on a great circle? Because of the symmetry of the sphere, one might expect that the distribution is uniform and independent of the choice of coordinates. However, two analyses give contradictory results. First, note that choosing a point uniformly on the sphere is equivalent to choosing the longitude \lambda uniformly from \pi,\pi/math> and choosing the latitude \varphi from \frac,\frac/math> with density \frac \cos \varphi. Then we can look at two different great circles: # If the coordinates are chosen so that the great circle is an equator (latitude \varphi = 0), the conditional ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conditional Probability Distribution
In probability theory and statistics, the conditional probability distribution is a probability distribution that describes the probability of an outcome given the occurrence of a particular event. Given two jointly distributed random variables X and Y, the conditional probability distribution of Y given X is the probability distribution of Y when X is known to be a particular value; in some cases the conditional probabilities may be expressed as functions containing the unspecified value x of X as a parameter. When both X and Y are categorical variables, a conditional probability table is typically used to represent the conditional probability. The conditional distribution contrasts with the marginal distribution of a random variable, which is its distribution without reference to the value of the other variable. If the conditional distribution of Y given X is a continuous distribution, then its probability density function is known as the conditional density function. The prop ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Leibniz Integral Rule
In calculus, the Leibniz integral rule for differentiation under the integral sign, named after Gottfried Wilhelm Leibniz, states that for an integral of the form \int_^ f(x,t)\,dt, where -\infty < a(x), b(x) < \infty and the integrands are functions dependent on the derivative of this integral is expressible as where the partial derivative indicates that inside the integral, only the variation of with is considered in taking the derivative. In the special case where the functions and |
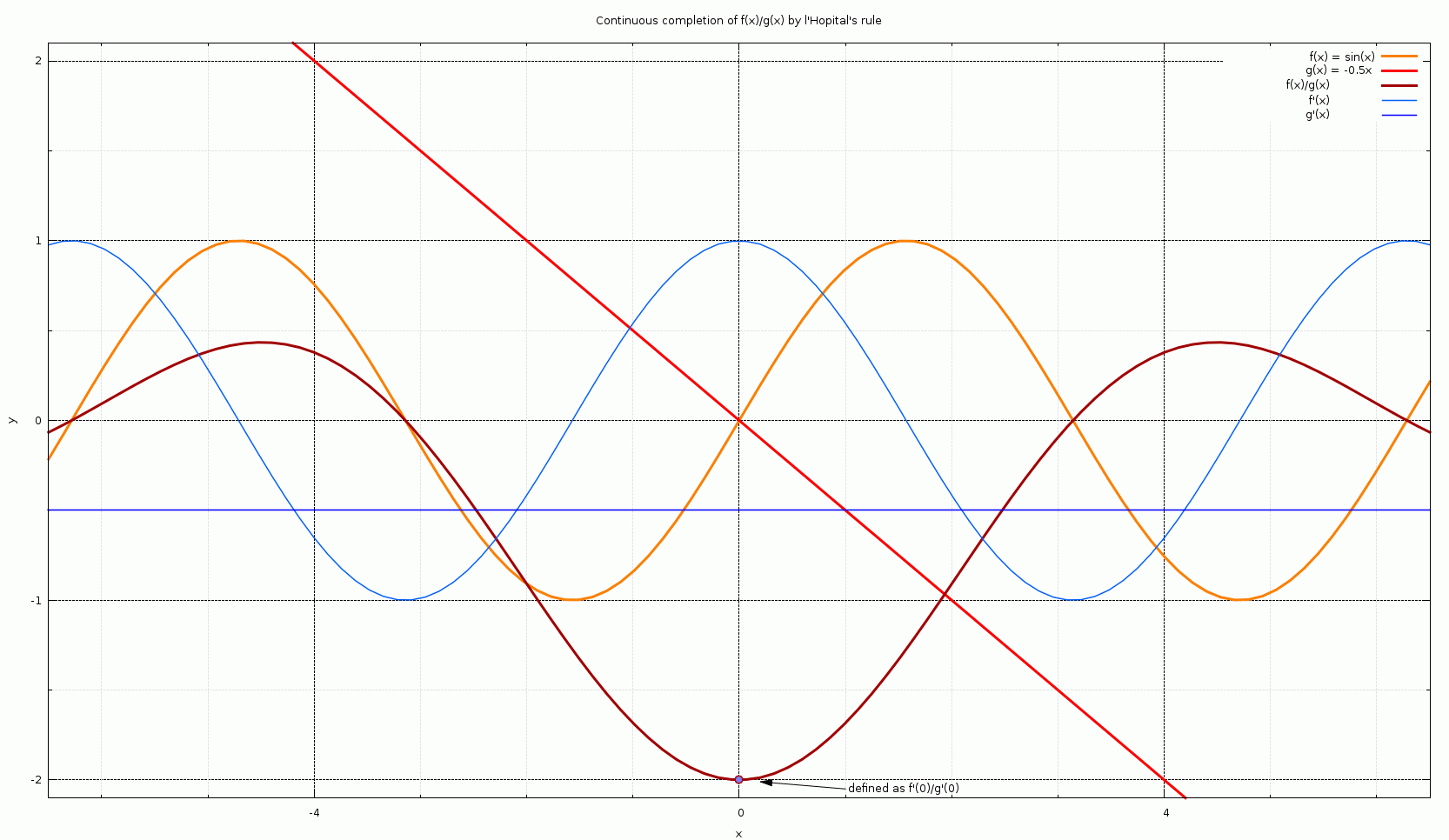
L'Hôpital's Rule
L'Hôpital's rule (, ), also known as Bernoulli's rule, is a mathematical theorem that allows evaluating limits of indeterminate forms using derivatives. Application (or repeated application) of the rule often converts an indeterminate form to an expression that can be easily evaluated by substitution. The rule is named after the 17th-century French mathematician Guillaume de l'Hôpital. Although the rule is often attributed to de l'Hôpital, the theorem was first introduced to him in 1694 by the Swiss mathematician Johann Bernoulli. L'Hôpital's rule states that for functions and which are defined on an open interval and differentiable on I\setminus \ for a (possibly infinite) accumulation point of , if \lim \limits_f(x)=\lim \limits_g(x)=0 \text\pm\infty, and g'(x)\ne 0 for all in I\setminus \, and \lim \limits_\frac exists, then :\lim_\frac = \lim_\frac. The differentiation of the numerator and denominator often simplifies the quotient or converts it to a limit t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Limit (mathematics)
In mathematics, a limit is the value that a function (or sequence) approaches as the argument (or index) approaches some value. Limits of functions are essential to calculus and mathematical analysis, and are used to define continuity, derivatives, and integrals. The concept of a limit of a sequence is further generalized to the concept of a limit of a topological net, and is closely related to limit and direct limit in category theory. The limit inferior and limit superior provide generalizations of the concept of a limit which are particularly relevant when the limit at a point may not exist. Notation In formulas, a limit of a function is usually written as : \lim_ f(x) = L, and is read as "the limit of of as approaches equals ". This means that the value of the function can be made arbitrarily close to , by choosing sufficiently close to . Alternatively, the fact that a function approaches the limit as approaches is sometimes denoted by a right arrow (→ or ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Defined And Undefined
In mathematics, the term undefined refers to a value, function, or other expression that cannot be assigned a meaning within a specific formal system. Attempting to assign or use an undefined value within a particular formal system, may produce contradictory or meaningless results within that system. In practice, mathematicians may use the term ''undefined'' to warn that a particular calculation or property can produce mathematically inconsistent results, and therefore, it should be avoided. Caution must be taken to avoid the use of such undefined values in a deduction or proof. Whether a particular function or value is undefined, depends on the rules of the formal system in which it is used. For example, the imaginary number \sqrt is undefined within the set of real numbers. So it is meaningless to reason about the value, solely within the discourse of real numbers. However, defining the imaginary number i to be equal to \sqrt, allows there to be a consistent set of m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Goodman–Nguyen–Van Fraassen Algebra
In probability theory, a conditional event algebra (CEA) is an alternative to a standard, Boolean algebra of possible events (a set of possible events related to one another by the familiar operations ''and'', ''or'', and ''not'') that contains not just ordinary events but also conditional events that have the form "if ''A'', then ''B''". The usual motivation for a CEA is to ground the definition of a probability function for events, ''P'', that satisfies the equation ''P''(if ''A'' then ''B'') = ''P''(''A'' and ''B'') / ''P''(''A''). Motivation In standard probability theory the occurrence of an event corresponds to a set of possible outcomes, each of which is an outcome that corresponds to the occurrence of the event. ''P''(''A''), the probability of event ''A'', is the sum of the probabilities of all outcomes that correspond to event ''A''; ''P''(''B'') is the sum of the probabilities of all outcomes that correspond to event ''B''; and ''P''(''A'' and ''B'') is the sum of the pro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |