|
Epanechnikov Distribution
In probability theory and statistics, the U-quadratic distribution is a continuous probability distribution defined by a unique convex quadratic function with lower limit ''a'' and upper limit ''b''. : f(x, a,b,\alpha, \beta)=\alpha \left ( x - \beta \right )^2, \quad\text x \in , b Parameter relations This distribution has effectively only two parameters ''a'', ''b'', as the other two are explicit functions of the support defined by the former two parameters: : \beta = (gravitational balance center, offset), and : \alpha = (vertical scale). Related distributions One can introduce a vertically inverted (\cap)-quadratic distribution in analogous fashion. That inverted distribution is also closely related to the Epanechnikov distribution. Applications This distribution is a useful model for symmetric bimodal processes. Other continuous distributions allow more flexibility, in terms of relaxing the symmetry and the quadratic shape of the density function, which are enforc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Distributions UQuadratic PDF
Distribution may refer to: Mathematics *Distribution (mathematics), generalized functions used to formulate solutions of partial differential equations *Probability distribution, the probability of a particular value or value range of a variable **Cumulative distribution function, in which the probability of being no greater than a particular value is a function of that value *Frequency distribution, a list of the values recorded in a sample * Inner distribution, and outer distribution, in coding theory *Distribution (differential geometry), a subset of the tangent bundle of a manifold *Distributed parameter system, systems that have an infinite-dimensional state-space *Distribution of terms, a situation in which all members of a category are accounted for *Distributivity, a property of binary operations that generalises the distributive law from elementary algebra *Distribution (number theory) *Distribution problems, a common type of problems in combinatorics where the goal i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Moment Generating Function
In probability theory and statistics, the moment-generating function of a real-valued random variable is an alternative specification of its probability distribution. Thus, it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or cumulative distribution functions. There are particularly simple results for the moment-generating functions of distributions defined by the weighted sums of random variables. However, not all random variables have moment-generating functions. As its name implies, the moment-generating function can be used to compute a distribution’s moments: the -th moment about 0 is the -th derivative of the moment-generating function, evaluated at 0. In addition to univariate real-valued distributions, moment-generating functions can also be defined for vector- or matrix-valued random variables, and can even be extended to more general cases. The moment-generating function of a real-valu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Characteristic Function
In mathematics, the term "characteristic function" can refer to any of several distinct concepts: * The indicator function of a subset, that is the function \mathbf_A\colon X \to \, which for a given subset ''A'' of ''X'', has value 1 at points of ''A'' and 0 at points of ''X'' − ''A''. * The characteristic function in convex analysis, closely related to the indicator function of a set: \chi_A (x) := \begin 0, & x \in A; \\ + \infty, & x \not \in A. \end * In probability theory, the characteristic function of any probability distribution on the real line is given by the following formula, where ''X'' is any random variable with the distribution in question: \varphi_X(t) = \operatorname\left(e^\right), where \operatorname denotes expected value. For multivariate distributions, the product ''tX'' is replaced by a scalar product of vectors. * The characteristic function of a cooperative game in game theory. * The characteristic polynomial in linear algebra. * ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Theory
Probability theory or probability calculus is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expressing it through a set of axioms of probability, axioms. Typically these axioms formalise probability in terms of a probability space, which assigns a measure (mathematics), measure taking values between 0 and 1, termed the probability measure, to a set of outcomes called the sample space. Any specified subset of the sample space is called an event (probability theory), event. Central subjects in probability theory include discrete and continuous random variables, probability distributions, and stochastic processes (which provide mathematical abstractions of determinism, non-deterministic or uncertain processes or measured Quantity, quantities that may either be single occurrences or evolve over time in a random fashion). Although it is no ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German language, German: ', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of statistical survey, surveys and experimental design, experiments. When census data (comprising every member of the target population) cannot be collected, statisticians collect data by developing specific experiment designs and survey sample (statistics), samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Distribution
In probability theory and statistics, a probability distribution is a Function (mathematics), function that gives the probabilities of occurrence of possible events for an Experiment (probability theory), experiment. It is a mathematical description of a Randomness, random phenomenon in terms of its sample space and the Probability, probabilities of Event (probability theory), events (subsets of the sample space). For instance, if is used to denote the outcome of a coin toss ("the experiment"), then the probability distribution of would take the value 0.5 (1 in 2 or 1/2) for , and 0.5 for (assuming that fair coin, the coin is fair). More commonly, probability distributions are used to compare the relative occurrence of many different random values. Probability distributions can be defined in different ways and for discrete or for continuous variables. Distributions with special properties or for especially important applications are given specific names. Introduction A prob ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Function
In mathematics, a real-valued function is called convex if the line segment between any two distinct points on the graph of a function, graph of the function lies above or on the graph between the two points. Equivalently, a function is convex if its epigraph (mathematics), ''epigraph'' (the set of points on or above the graph of the function) is a convex set. In simple terms, a convex function graph is shaped like a cup \cup (or a straight line like a linear function), while a concave function's graph is shaped like a cap \cap. A twice-differentiable function, differentiable function of a single variable is convex if and only if its second derivative is nonnegative on its entire domain of a function, domain. Well-known examples of convex functions of a single variable include a linear function f(x) = cx (where c is a real number), a quadratic function cx^2 (c as a nonnegative real number) and an exponential function ce^x (c as a nonnegative real number). Convex functions pl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Epanechnikov Distribution
In probability theory and statistics, the U-quadratic distribution is a continuous probability distribution defined by a unique convex quadratic function with lower limit ''a'' and upper limit ''b''. : f(x, a,b,\alpha, \beta)=\alpha \left ( x - \beta \right )^2, \quad\text x \in , b Parameter relations This distribution has effectively only two parameters ''a'', ''b'', as the other two are explicit functions of the support defined by the former two parameters: : \beta = (gravitational balance center, offset), and : \alpha = (vertical scale). Related distributions One can introduce a vertically inverted (\cap)-quadratic distribution in analogous fashion. That inverted distribution is also closely related to the Epanechnikov distribution. Applications This distribution is a useful model for symmetric bimodal processes. Other continuous distributions allow more flexibility, in terms of relaxing the symmetry and the quadratic shape of the density function, which are enforc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bimodal
In statistics, a multimodal distribution is a probability distribution with more than one mode (i.e., more than one local peak of the distribution). These appear as distinct peaks (local maxima) in the probability density function, as shown in Figures 1 and 2. Categorical, continuous, and discrete data can all form multimodal distributions. Among univariate analyses, multimodal distributions are commonly bimodal. Terminology When the two modes are unequal the larger mode is known as the major mode and the other as the minor mode. The least frequent value between the modes is known as the antimode. The difference between the major and minor modes is known as the amplitude. In time series the major mode is called the acrophase and the antimode the batiphase. Galtung's classification Galtung introduced a classification system (AJUS) for distributions: *A: unimodal distribution – peak in the middle *J: unimodal – peak at either end *U: bimodal – peaks at both ends ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Beta Distribution
In probability theory and statistics, the beta distribution is a family of continuous probability distributions defined on the interval [0, 1] or (0, 1) in terms of two positive Statistical parameter, parameters, denoted by ''alpha'' (''α'') and ''beta'' (''β''), that appear as exponents of the variable and its complement to 1, respectively, and control the shape parameter, shape of the distribution. The beta distribution has been applied to model the behavior of random variables limited to intervals of finite length in a wide variety of disciplines. The beta distribution is a suitable model for the random behavior of percentages and proportions. In Bayesian inference, the beta distribution is the conjugate prior distribution, conjugate prior probability distribution for the Bernoulli distribution, Bernoulli, binomial distribution, binomial, negative binomial distribution, negative binomial, and geometric distribution, geometric distributions. The formulation of the beta dist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
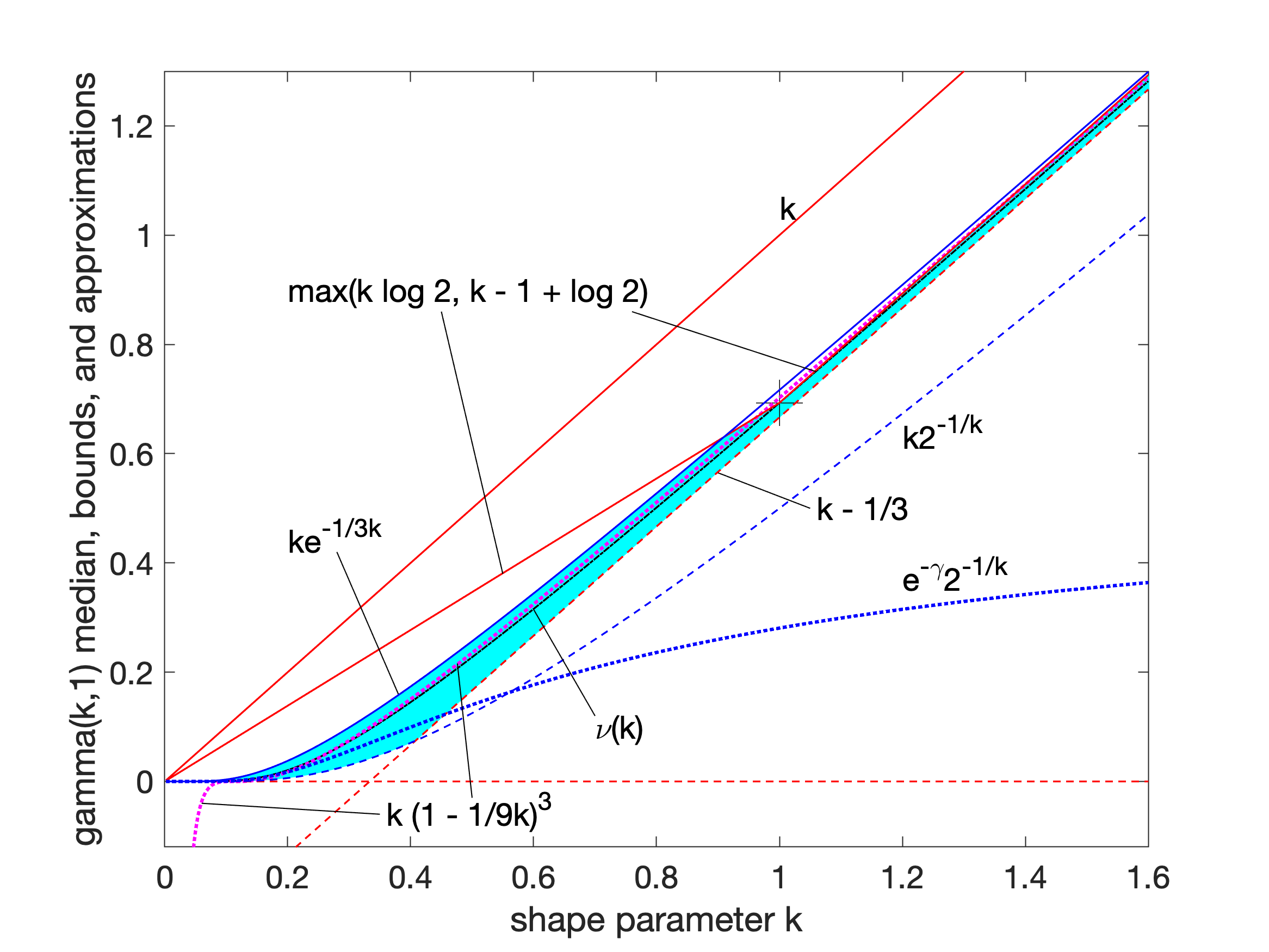
Gamma Distribution
In probability theory and statistics, the gamma distribution is a versatile two-parameter family of continuous probability distributions. The exponential distribution, Erlang distribution, and chi-squared distribution are special cases of the gamma distribution. There are two equivalent parameterizations in common use: # With a shape parameter and a scale parameter # With a shape parameter \alpha and a rate parameter In each of these forms, both parameters are positive real numbers. The distribution has important applications in various fields, including econometrics, Bayesian statistics, and life testing. In econometrics, the (''α'', ''θ'') parameterization is common for modeling waiting times, such as the time until death, where it often takes the form of an Erlang distribution for integer ''α'' values. Bayesian statisticians prefer the (''α'',''λ'') parameterization, utilizing the gamma distribution as a conjugate prior for several inverse scale parameters, facilit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |