|
Discrete Weighted Transform
Discrete may refer to: *Discrete particle or quantum in physics, for example in quantum theory *Discrete device, an electronic component with just one circuit element, either passive or active, other than an integrated circuit *Discrete group, a group with the discrete topology *Discrete category, category whose only arrows are identity arrows *Discrete mathematics, the study of structures without continuity *Discrete optimization, a branch of optimization in applied mathematics and computer science *Discrete probability distribution, a random variable that can be counted *Discrete space, a simple example of a topological space *Discrete spline interpolation, the discrete analog of ordinary spline interpolation * Discrete time, non-continuous time, which results in discrete-time samples *Discrete variable In mathematics and statistics, a quantitative variable may be continuous or discrete. If it can take on two real values and all the values between them, the variable is co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum
In physics, a quantum (: quanta) is the minimum amount of any physical entity (physical property) involved in an interaction. The fundamental notion that a property can be "quantized" is referred to as "the hypothesis of quantization". This means that the magnitude of the physical property can take on only discrete values consisting of integer multiples of one quantum. For example, a photon is a single quantum of light of a specific frequency (or of any other form of electromagnetic radiation). Similarly, the energy of an electron bound within an atom is quantized and can exist only in certain discrete values. Atoms and matter in general are stable because electrons can exist only at discrete energy levels within an atom. Quantization is one of the foundations of the much broader physics of quantum mechanics. Quantization of energy and its influence on how energy and matter interact (quantum electrodynamics) is part of the fundamental framework for understanding and describing ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discrete Device
An electronic component is any basic discrete electronic device or physical entity part of an electronic system used to affect electrons or their associated fields. Electronic components are mostly industrial products, available in a singular form and are not to be confused with electrical elements, which are conceptual abstractions representing idealized electronic components and elements. A datasheet for an electronic component is a technical document that provides detailed information about the component's specifications, characteristics, and performance. Discrete circuits are made of individual electronic components that only perform one function each as packaged, which are known as discrete components, although strictly the term discrete component refers to such a component with semiconductor material such as individual transistors. Electronic components have a number of electrical terminals or leads. These leads connect to other electrical components, often over wire, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discrete Group
In mathematics, a topological group ''G'' is called a discrete group if there is no limit point in it (i.e., for each element in ''G'', there is a neighborhood which only contains that element). Equivalently, the group ''G'' is discrete if and only if its identity is isolated. A subgroup ''H'' of a topological group ''G'' is a discrete subgroup if ''H'' is discrete when endowed with the subspace topology from ''G''. In other words there is a neighbourhood of the identity in ''G'' containing no other element of ''H''. For example, the integers, Z, form a discrete subgroup of the reals, R (with the standard metric topology), but the rational numbers, Q, do not. Any group can be endowed with the discrete topology, making it a discrete topological group. Since every map from a discrete space is continuous, the topological homomorphisms between discrete groups are exactly the group homomorphisms between the underlying groups. Hence, there is an isomorphism between the catego ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discrete Category
In mathematics, in the field of category theory, a discrete category is a category whose only morphisms are the identity morphisms: :hom''C''(''X'', ''X'') = {id''X''} for all objects ''X'' :hom''C''(''X'', ''Y'') = ∅ for all objects ''X'' ≠ ''Y'' Since by axioms, there is always the identity morphism between the same object, we can express the above as condition on the cardinality of the hom-set :, hom''C''(''X'', ''Y'') , is 1 when ''X'' = ''Y'' and 0 when ''X'' is not equal to ''Y''. Some authors prefer a weaker notion, where a discrete category merely needs to be equivalent to such a category. Simple facts Any class of objects defines a discrete category when augmented with identity maps. Any subcategory of a discrete category is discrete. Also, a category is discrete if and only if all of its subcategories are full. The limit of any functor from a discrete category into another category is called a product, while the colimit is called a coproduct. Thus, for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Identity Morphism
In mathematics, a morphism is a concept of category theory that generalizes structure-preserving maps such as homomorphism between algebraic structures, functions from a set to another set, and continuous functions between topological spaces. Although many examples of morphisms are structure-preserving maps, morphisms need not to be maps, but they can be composed in a way that is similar to function composition. Morphisms and objects are constituents of a category. Morphisms, also called ''maps'' or ''arrows'', relate two objects called the ''source'' and the ''target'' of the morphism. There is a partial operation, called ''composition'', on the morphisms of a category that is defined if the target of the first morphism equals the source of the second morphism. The composition of morphisms behaves like function composition ( associativity of composition when it is defined, and existence of an identity morphism for every object). Morphisms and categories recur in much of cont ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discrete Mathematics
Discrete mathematics is the study of mathematical structures that can be considered "discrete" (in a way analogous to discrete variables, having a bijection with the set of natural numbers) rather than "continuous" (analogously to continuous functions). Objects studied in discrete mathematics include integers, Graph (discrete mathematics), graphs, and Statement (logic), statements in Mathematical logic, logic. By contrast, discrete mathematics excludes topics in "continuous mathematics" such as real numbers, calculus or Euclidean geometry. Discrete objects can often be enumeration, enumerated by integers; more formally, discrete mathematics has been characterized as the branch of mathematics dealing with countable sets (finite sets or sets with the same cardinality as the natural numbers). However, there is no exact definition of the term "discrete mathematics". The set of objects studied in discrete mathematics can be finite or infinite. The term finite mathematics is sometime ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discrete Optimization
Discrete optimization is a branch of optimization in applied mathematics and computer science. As opposed to continuous optimization, some or all of the variables used in a discrete optimization problem are restricted to be discrete variables—that is, to assume only a discrete set of values, such as the integer An integer is the number zero (0), a positive natural number (1, 2, 3, ...), or the negation of a positive natural number (−1, −2, −3, ...). The negations or additive inverses of the positive natural numbers are referred to as negative in ...s. Branches Three notable branches of discrete optimization are:. * combinatorial optimization, which refers to problems on graphs, matroids and other discrete structures * integer programming * constraint programming These branches are all closely intertwined however, since many combinatorial optimization problems can be modeled as integer programs (e.g. shortest path) or constraint programs, any constraint pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discrete Probability Distribution
In probability theory and statistics, a probability distribution is a function that gives the probabilities of occurrence of possible events for an experiment. It is a mathematical description of a random phenomenon in terms of its sample space and the probabilities of events (subsets of the sample space). For instance, if is used to denote the outcome of a coin toss ("the experiment"), then the probability distribution of would take the value 0.5 (1 in 2 or 1/2) for , and 0.5 for (assuming that the coin is fair). More commonly, probability distributions are used to compare the relative occurrence of many different random values. Probability distributions can be defined in different ways and for discrete or for continuous variables. Distributions with special properties or for especially important applications are given specific names. Introduction A probability distribution is a mathematical description of the probabilities of events, subsets of the sample space. The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discrete Space
In topology, a discrete space is a particularly simple example of a topological space or similar structure, one in which the points form a , meaning they are '' isolated'' from each other in a certain sense. The discrete topology is the finest topology that can be given on a set. Every subset is open in the discrete topology so that in particular, every singleton subset is an open set in the discrete topology. Definitions Given a set X: A metric space (E,d) is said to be '' uniformly discrete'' if there exists a ' r > 0 such that, for any x,y \in E, one has either x = y or d(x,y) > r. The topology underlying a metric space can be discrete, without the metric being uniformly discrete: for example the usual metric on the set \left\. Properties The underlying uniformity on a discrete metric space is the discrete uniformity, and the underlying topology on a discrete uniform space is the discrete topology. Thus, the different notions of discrete space are compatible with on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discrete Spline Interpolation
In the mathematical field of numerical analysis, discrete spline interpolation is a form of interpolation where the interpolant is a special type of piecewise polynomial called a discrete spline. A discrete spline is a piecewise polynomial such that its central differences are continuous at the knots whereas a spline is a piecewise polynomial such that its derivative In mathematics, the derivative is a fundamental tool that quantifies the sensitivity to change of a function's output with respect to its input. The derivative of a function of a single variable at a chosen input value, when it exists, is t ...s are continuous at the knots. Discrete cubic splines are discrete splines where the central differences of orders 0, 1, and 2 are required to be continuous. Discrete splines were introduced by Mangasarin and Schumaker in 1971 as solutions of certain minimization problems involving differences. Discrete cubic splines Let ''x''1, ''x''2, . . ., ''x''''n''-1 be an incre ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discrete Time
In mathematical dynamics, discrete time and continuous time are two alternative frameworks within which variables that evolve over time are modeled. Discrete time Discrete time views values of variables as occurring at distinct, separate "points in time", or equivalently as being unchanged throughout each non-zero region of time ("time period")—that is, time is viewed as a discrete variable. Thus a non-time variable jumps from one value to another as time moves from one time period to the next. This view of time corresponds to a digital clock that gives a fixed reading of 10:37 for a while, and then jumps to a new fixed reading of 10:38, etc. In this framework, each variable of interest is measured once at each time period. The number of measurements between any two time periods is finite. Measurements are typically made at sequential integer values of the variable "time". A discrete signal or discrete-time signal is a time series consisting of a sequence of quantities. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
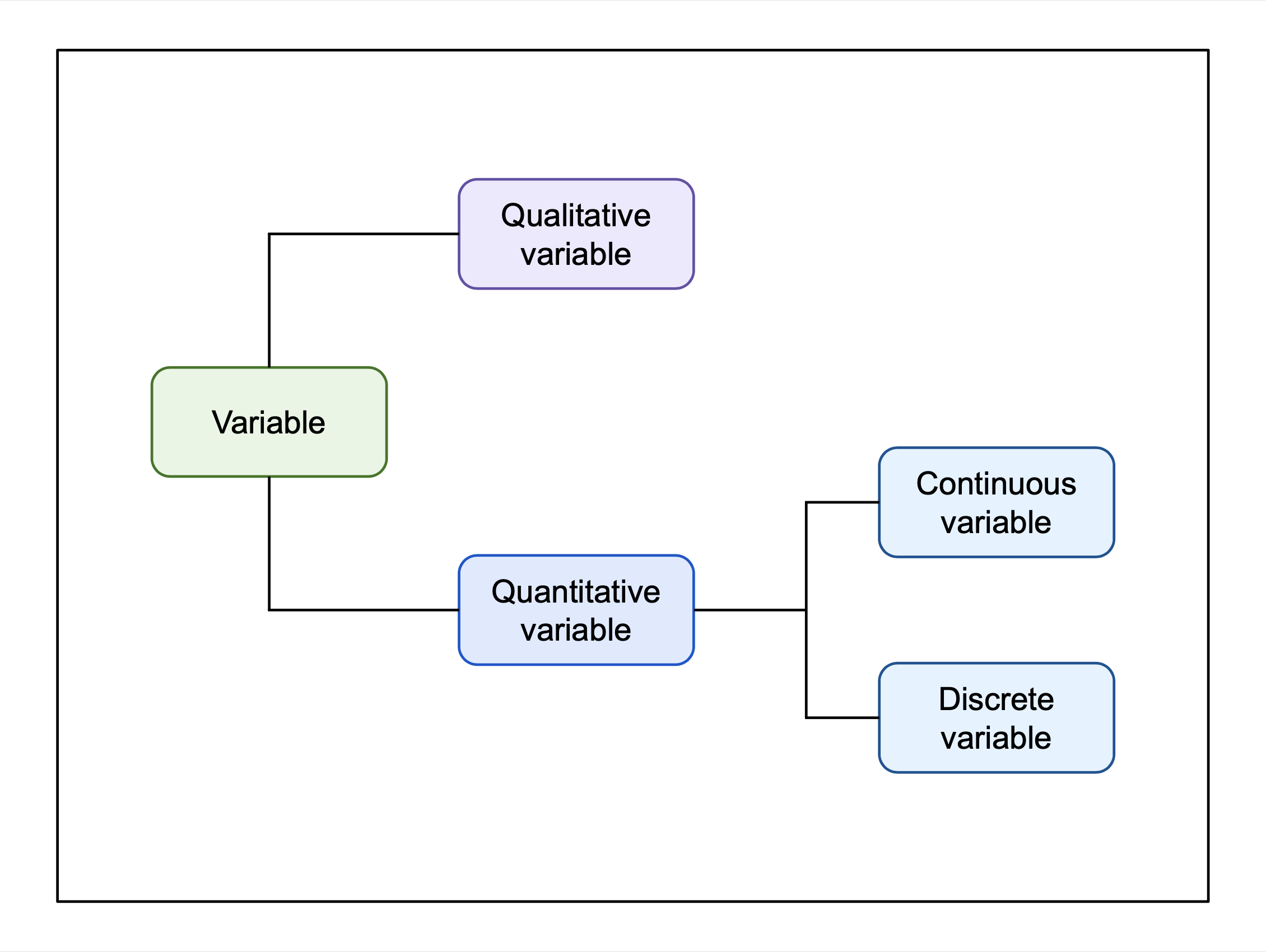
Discrete Variable
In mathematics and statistics, a quantitative variable may be continuous or discrete. If it can take on two real values and all the values between them, the variable is continuous in that interval. If it can take on a value such that there is a non-infinitesimal gap on each side of it containing no values that the variable can take on, then it is discrete around that value. In some contexts, a variable can be discrete in some ranges of the number line and continuous in others. In statistics, continuous and discrete variables are distinct statistical data types which are described with different probability distributions. Continuous variable A continuous variable is a variable such that there are possible values between any two values. For example, a variable over a non-empty range of the real numbers is continuous if it can take on any value in that range. Methods of calculus are often used in problems in which the variables are continuous, for example in continuous optimi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |