|
Classical Central-force Problem
In classical mechanics, the central-force problem is to determine the motion of a particle in a single central force, central potential field. A central force is a force (possibly negative) that points from the particle directly towards a fixed point in space, the center, and whose magnitude only depends on the distance of the object to the center. In a few important cases, the problem can be solved analytically, i.e., in terms of well-studied functions such as trigonometric functions. The solution of this problem is important to classical mechanics, since many naturally occurring forces are central. Examples include gravity and electromagnetism as described by Newton's law of universal gravitation and Coulomb's law, respectively. The problem is also important because some more complicated problems in classical physics (such as the two-body problem with forces along the line connecting the two bodies) can be reduced to a central-force problem. Finally, the solution to the centra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Central Force
In classical mechanics, a central force on an object is a force that is directed towards or away from a point called center of force. \mathbf(\mathbf) = F( \mathbf ) where F is a force vector, ''F'' is a scalar valued force function (whose absolute value gives the magnitude of the force and is positive if the force is outward and negative if the force is inward), r is the position vector, , , r, , is its length, and \hat = \mathbf r / \, \mathbf r\, is the corresponding unit vector. Not all central force fields are conservative or spherically symmetric. However, a central force is conservative if and only if it is spherically symmetric or rotationally invariant. Examples of spherically symmetric central forces include the Coulomb force and the force of gravity. Properties Central forces that are conservative can always be expressed as the negative gradient of a potential energy: \mathbf(\mathbf) = - \mathbf V(\mathbf) \; \text V(\mathbf) = \int_^ F(r)\,\mathrmr (the upper ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kinetic Energy
In physics, the kinetic energy of an object is the form of energy that it possesses due to its motion. In classical mechanics, the kinetic energy of a non-rotating object of mass ''m'' traveling at a speed ''v'' is \fracmv^2.Resnick, Robert and Halliday, David (1960) ''Physics'', Section 7-5, Wiley International Edition The kinetic energy of an object is equal to the work, or force ( F) in the direction of motion times its displacement ( s), needed to accelerate the object from rest to its given speed. The same amount of work is done by the object when decelerating from its current speed to a state of rest. The SI unit of energy is the joule, while the English unit of energy is the foot-pound. In relativistic mechanics, \fracmv^2 is a good approximation of kinetic energy only when ''v'' is much less than the speed of light. History and etymology The adjective ''kinetic'' has its roots in the Greek word κίνησις ''kinesis'', meaning "motion". The dichoto ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angular Momentum
Angular momentum (sometimes called moment of momentum or rotational momentum) is the rotational analog of Momentum, linear momentum. It is an important physical quantity because it is a Conservation law, conserved quantity – the total angular momentum of a closed system remains constant. Angular momentum has both a direction (geometry), direction and a magnitude, and both are conserved. Bicycle and motorcycle dynamics, Bicycles and motorcycles, flying discs, Rifling, rifled bullets, and gyroscopes owe their useful properties to conservation of angular momentum. Conservation of angular momentum is also why hurricanes form spirals and neutron stars have high rotational rates. In general, conservation limits the possible motion of a system, but it does not uniquely determine it. The three-dimensional angular momentum for a point particle is classically represented as a pseudovector , the cross product of the particle's position vector (relative to some origin) and its mo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
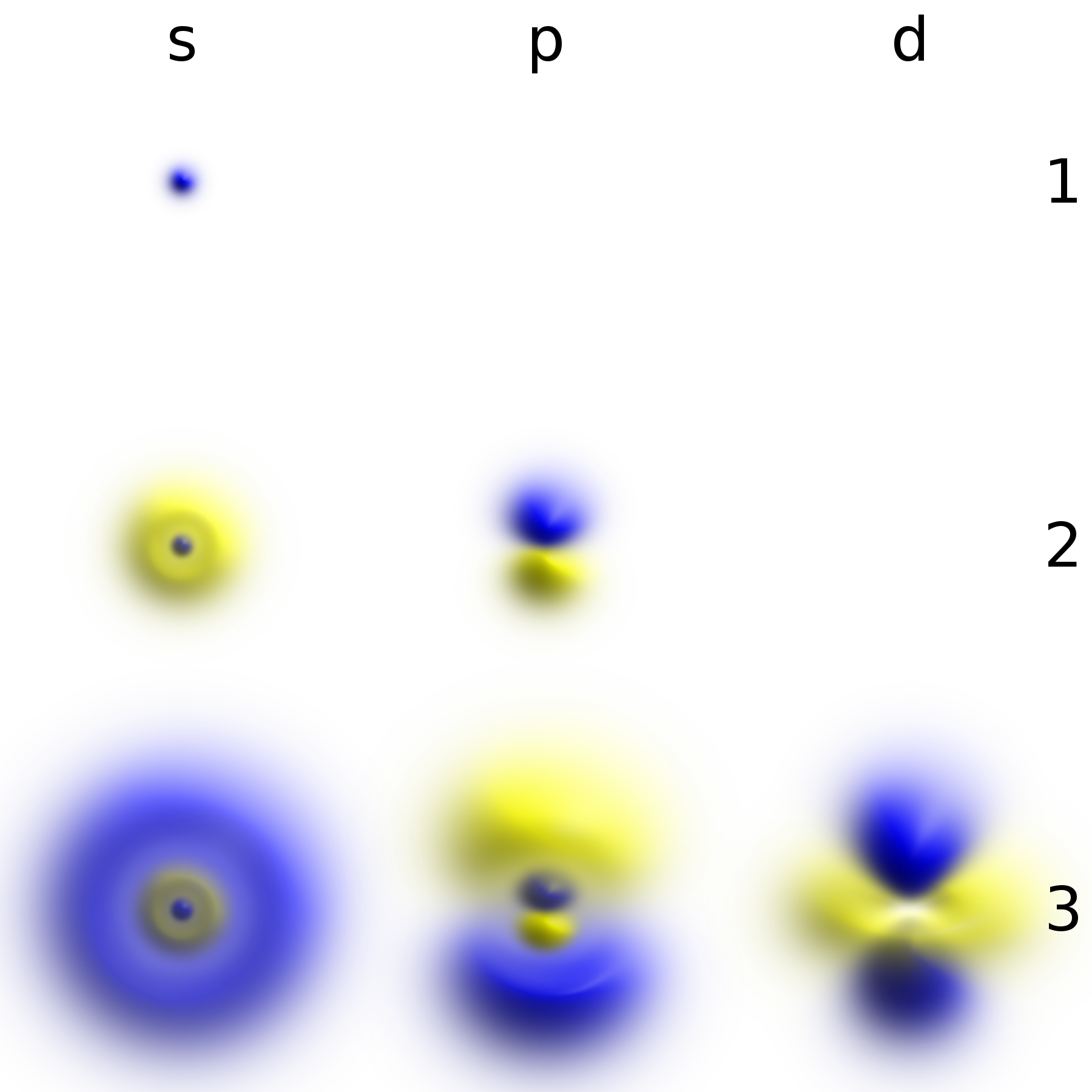
Particle In A Spherically Symmetric Potential
In quantum mechanics, a spherically symmetric potential is a system of which the potential only depends on the radial distance from the spherical center and a location in space. A particle in a spherically symmetric potential will behave accordingly to said potential and can therefore be used as an approximation, for example, of the electron in a hydrogen atom or of the formation of chemical bonds. In the general time-independent case, the dynamics of a particle in a spherically symmetric potential are governed by a Hamiltonian of the following form:\hat = \frac + V() Here, m_0 is the mass of the particle, \hat is the momentum operator, and the potential V(r) depends only on the vector magnitude of the position vector, that is, the radial distance from the origin (hence the spherical symmetry of the problem). To describe a particle in a spherically symmetric system, it is convenient to use spherical coordinates; denoted by r, \theta and \phi. The time-independent Schrödin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Mechanics
Quantum mechanics is the fundamental physical Scientific theory, theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is the foundation of all quantum physics, which includes quantum chemistry, quantum field theory, quantum technology, and quantum information science. Quantum mechanics can describe many systems that classical physics cannot. Classical physics can describe many aspects of nature at an ordinary (macroscopic and Microscopic scale, (optical) microscopic) scale, but is not sufficient for describing them at very small submicroscopic (atomic and subatomic) scales. Classical mechanics can be derived from quantum mechanics as an approximation that is valid at ordinary scales. Quantum systems have Bound state, bound states that are Quantization (physics), quantized to Discrete mathematics, discrete values of energy, momentum, angular momentum, and ot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
General Relativity
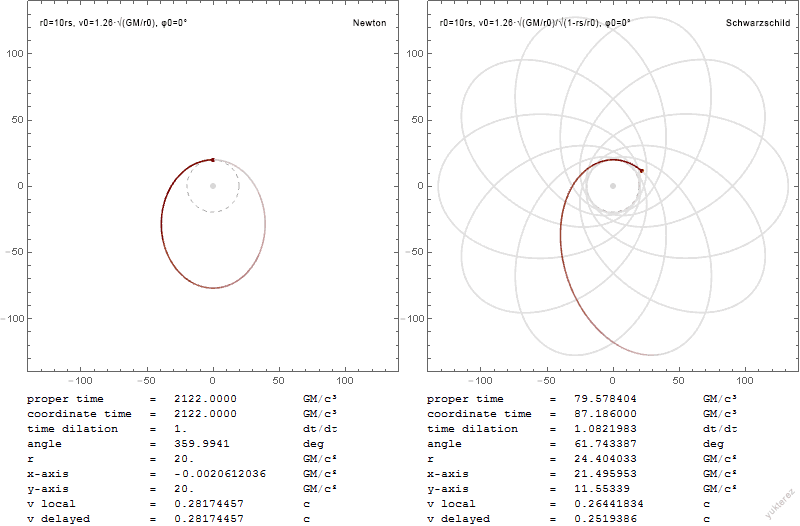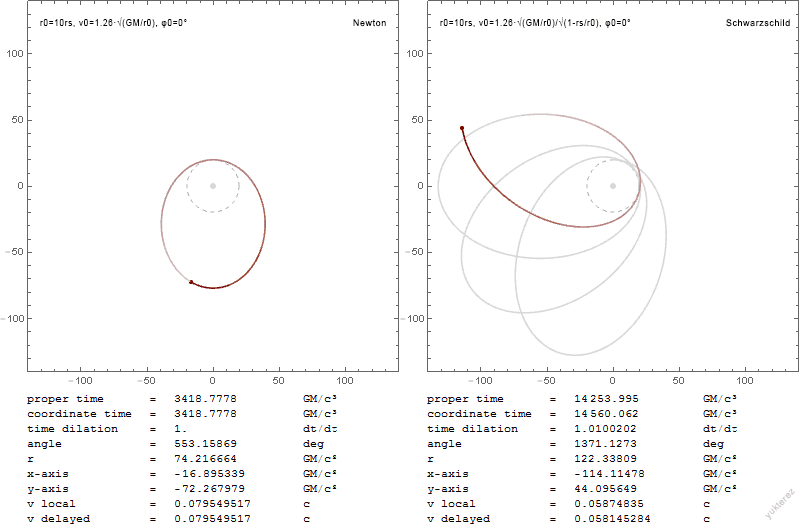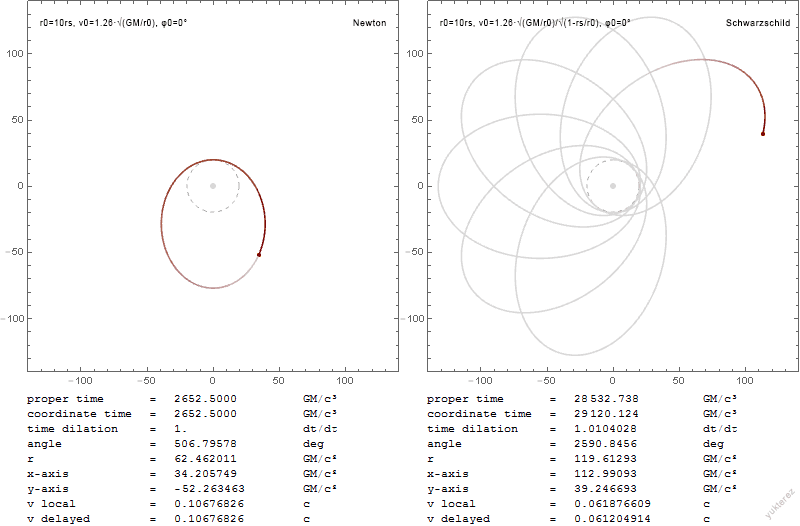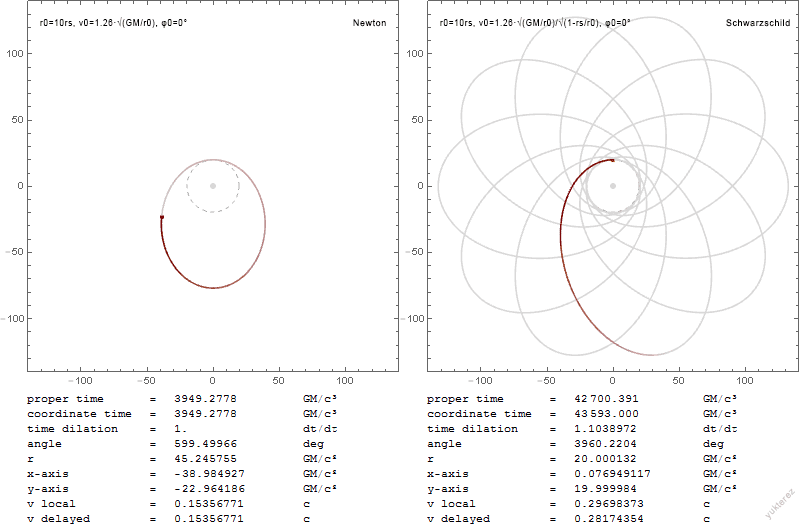
General relativity, also known as the general theory of relativity, and as Einstein's theory of gravity, is the differential geometry, geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of gravitation in modern physics. General theory of relativity, relativity generalizes special relativity and refines Newton's law of universal gravitation, providing a unified description of gravity as a geometric property of space and time in physics, time, or four-dimensional spacetime. In particular, the ''curvature of spacetime'' is directly related to the energy and momentum of whatever is present, including matter and radiation. The relation is specified by the Einstein field equations, a system of second-order partial differential equations. Newton's law of universal gravitation, which describes gravity in classical mechanics, can be seen as a prediction of general relativity for the almost flat spacetime geometry around stationary mass ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Schwarzschild Geodesics
In general relativity, Schwarzschild geodesics describe the motion of test particles in the gravitational field of a central fixed mass M, that is, motion in the Schwarzschild metric. Schwarzschild geodesics have been pivotal in the tests of general relativity, validation of Einstein's theory of general relativity. For example, they provide accurate predictions of the Anomalous perihelion precession, anomalous Precession#Relativistic (Einsteinian), precession of the planets in the Solar System and of the deflection of light by gravity. Schwarzschild geodesics pertain only to the motion of particles of masses so small they contribute little to the gravitational field. However, they are highly accurate in many astrophysical scenarios provided that m is many-fold smaller than the central mass M, e.g., for planets orbiting their star. Schwarzschild geodesics are also a good approximation to the relative motion of two bodies of arbitrary mass, provided that the Schwarzschild mass M is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spherical Symmetry
In geometry, circular symmetry is a type of continuous symmetry for a planar object that can be rotated by any arbitrary angle and map onto itself. Rotational circular symmetry is isomorphic with the circle group in the complex plane, or the special orthogonal group SO(2), and unitary group U(1). Reflective circular symmetry is isomorphic with the orthogonal group O(2). Two dimensions A 2-dimensional object with circular symmetry would consist of concentric circles and annular domains. Rotational circular symmetry has all cyclic symmetry, Z''n'' as subgroup symmetries. Reflective circular symmetry has all dihedral symmetry, Dih''n'' as subgroup symmetries. Three dimensions In 3-dimensions, a surface or solid of revolution has circular symmetry around an axis, also called cylindrical symmetry or axial symmetry. An example is a right circular cone. Circular symmetry in 3 dimensions has all pyramidal symmetry, C''n''v as subgroups. A double-cone, bicone, cyli ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scalar Potential
In mathematical physics, scalar potential describes the situation where the difference in the potential energies of an object in two different positions depends only on the positions, not upon the path taken by the object in traveling from one position to the other. It is a scalar field in three-space: a directionless value ( scalar) that depends only on its location. A familiar example is potential energy due to gravity. A ''scalar potential'' is a fundamental concept in vector analysis and physics (the adjective ''scalar'' is frequently omitted if there is no danger of confusion with '' vector potential''). The scalar potential is an example of a scalar field. Given a vector field , the scalar potential is defined such that: \mathbf = -\nabla P = - \left( \frac, \frac, \frac \right), where is the gradient of and the second part of the equation is minus the gradient for a function of the Cartesian coordinates . In some cases, mathematicians may use a positive sign ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spherical Coordinate System
In mathematics, a spherical coordinate system specifies a given point in three-dimensional space by using a distance and two angles as its three coordinates. These are * the radial distance along the line connecting the point to a fixed point called the origin; * the polar angle between this radial line and a given ''polar axis''; and * the azimuthal angle , which is the angle of rotation of the radial line around the polar axis. (See graphic regarding the "physics convention".) Once the radius is fixed, the three coordinates (''r'', ''θ'', ''φ''), known as a 3-tuple, provide a coordinate system on a sphere, typically called the spherical polar coordinates. The plane passing through the origin and perpendicular to the polar axis (where the polar angle is a right angle) is called the ''reference plane'' (sometimes '' fundamental plane''). Terminology The radial distance from the fixed point of origin is also called the ''radius'', or ''radial line'', or ''radial coor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant (as opposed to the total derivative, in which all variables are allowed to vary). Partial derivatives are used in vector calculus and differential geometry. The partial derivative of a function f(x, y, \dots) with respect to the variable x is variously denoted by It can be thought of as the rate of change of the function in the x-direction. Sometimes, for the partial derivative of z with respect to x is denoted as \tfrac. Since a partial derivative generally has the same arguments as the original function, its functional dependence is sometimes explicitly signified by the notation, such as in: f'_x(x, y, \ldots), \frac (x, y, \ldots). The symbol used to denote partial derivatives is ∂. One of the first known uses of this symbol in mathematics is by Marquis de Condorcet from 1770, who used it for partial differ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Del In Cylindrical And Spherical Coordinates
This is a list of some vector calculus formulae for working with common curvilinear coordinates, curvilinear coordinate systems. Notes * This article uses the standard notation ISO 80000-2, which supersedes ISO 31-11#Coordinate systems, ISO 31-11, for spherical coordinate system, spherical coordinates (other sources may reverse the definitions of ''θ'' and ''φ''): ** The polar angle is denoted by \theta \in [0, \pi]: it is the angle between the ''z''-axis and the radial vector connecting the origin to the point in question. ** The azimuthal angle is denoted by \varphi \in [0, 2\pi]: it is the angle between the ''x''-axis and the projection of the radial vector onto the ''xy''-plane. * The function can be used instead of the mathematical function owing to its Domain of a function, domain and Image (mathematics), image. The classical arctan function has an image of , whereas atan2 is defined to have an image of . Coordinate conversions Note that the operation \arctan\le ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |