|
Beta Coefficient
In finance, the beta ( or market beta or beta coefficient) is a statistic that measures the expected increase or decrease of an individual stock price in proportion to movements of the stock market as a whole. Beta can be used to indicate the contribution of an individual asset to the market risk of a portfolio when it is added in small quantity. It refers to an asset's non-diversifiable risk, systematic risk, or market risk. Beta is not a measure of idiosyncratic risk. Beta is the hedge ratio of an investment with respect to the stock market. For example, to hedge out the market-risk of a stock with a market beta of 2.0, an investor would short $2,000 in the stock market for every $1,000 invested in the stock. Thus insured, movements of the overall stock market no longer influence the combined position on average. Beta measures the contribution of an individual investment to the risk of the market portfolio that was not reduced by diversification. It does not measure the r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Finance
Finance refers to monetary resources and to the study and Academic discipline, discipline of money, currency, assets and Liability (financial accounting), liabilities. As a subject of study, is a field of Business administration, Business Administration wich study the planning, organizing, leading, and controlling of an organization's resources to achieve its goals. Based on the scope of financial activities in financial systems, the discipline can be divided into Personal finance, personal, Corporate finance, corporate, and public finance. In these financial systems, assets are bought, sold, or traded as financial instruments, such as Currency, currencies, loans, Bond (finance), bonds, Share (finance), shares, stocks, Option (finance), options, Futures contract, futures, etc. Assets can also be banked, Investment, invested, and Insurance, insured to maximize value and minimize loss. In practice, Financial risk, risks are always present in any financial action and entities. Due ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Put Option
In finance, a put or put option is a derivative instrument in financial markets that gives the holder (i.e. the purchaser of the put option) the right to sell an asset (the ''underlying''), at a specified price (the ''strike''), by (or on) a specified date (the '' expiry'' or ''maturity'') to the ''writer'' (i.e. seller) of the put. The purchase of a put option is interpreted as a negative sentiment about the future value of the underlying stock. page 15 , 4.2.3 Positive and negative sentiment The term "put" comes from the fact that the owner has the right to "put up for sale" the stock or index. Puts may also be combined with other derivatives as part of more complex investment strategies, and in particular, may be useful for hedging. Holding a European put option is equivalent to holding the corresponding call option and selling an appropriate forward contract. This equivalence is called " put-call parity". Put options are most commonly used in the stock market to prot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Levered Free Cash Flow
In corporate finance, free cash flow to equity (FCFE) is a metric of how much cash can be distributed to the equity shareholders of the company as dividends or stock buybacks—after all expenses, reinvestments, and debt repayments are taken care of. It is also referred to as the levered free cash flow or the flow to equity (FTE). Whereas dividends are the cash flows actually paid to shareholders, the FCFE is the cash flow simply available to shareholders. The FCFE is usually calculated as a part of DCF or LBO modelling and valuation. Basic formulae Assuming there is no preferred stock outstanding: : FCFE = FCFF + Net\ Borrowing - Interest*(1-t) where: * ''FCFF'' is the free cash flow to firm; * ''Net Borrowing'' is the difference between debt principals paid and raised; * ''Interest*(1–t)'' is the firm's after-tax interest expense. or : FCFE = NI + D\& A - Capex - \Delta WC + Net\ Borrowing or : FCFE = NI - 1-b) (Capex-D\& A) + (1-b) (\Delta WC) where: * ''NI'' is th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Risk-free Interest Rate
The risk-free rate of return, usually shortened to the risk-free rate, is the rate of return of a hypothetical investment with scheduled payments over a fixed period of time that is assumed to meet all payment obligations. Since the risk-free rate can be obtained with no risk, any other investment having some risk will have to have a higher rate of return in order to induce any investors to hold it. In practice, to infer the risk-free interest rate in a particular currency, market participants often choose the yield to maturity on a risk-free bond issued by a government of the same currency whose risks of default are so low as to be negligible. For example, the rate of return on zero-coupon Treasury bonds (T-bills) is sometimes seen as the risk-free rate of return in US dollars. Theoretical measurement As stated by Malcolm Kemp in chapter five of his book ''Market Consistency: Model Calibration in Imperfect Markets'', the risk-free rate means different things to different pe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Capital Asset Pricing Model
In finance, the capital asset pricing model (CAPM) is a model used to determine a theoretically appropriate required rate of return of an asset, to make decisions about adding assets to a Diversification (finance), well-diversified Portfolio (finance), portfolio. The model takes into account the asset's sensitivity to non-diversifiable risk (also known as systematic risk or market risk), often represented by the quantity Beta (finance), beta (β) in the financial industry, as well as the expected return of the market and the expected return of a theoretical Risk-free bond, risk-free asset. CAPM assumes a particular form of utility functions (in which only first and second Moment (mathematics), moments matter, that is risk is measured by variance, for example a quadratic utility) or alternatively asset returns whose probability distributions are completely described by the first two moments (for example, the normal distribution) and zero transaction costs (necessary for diversifi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
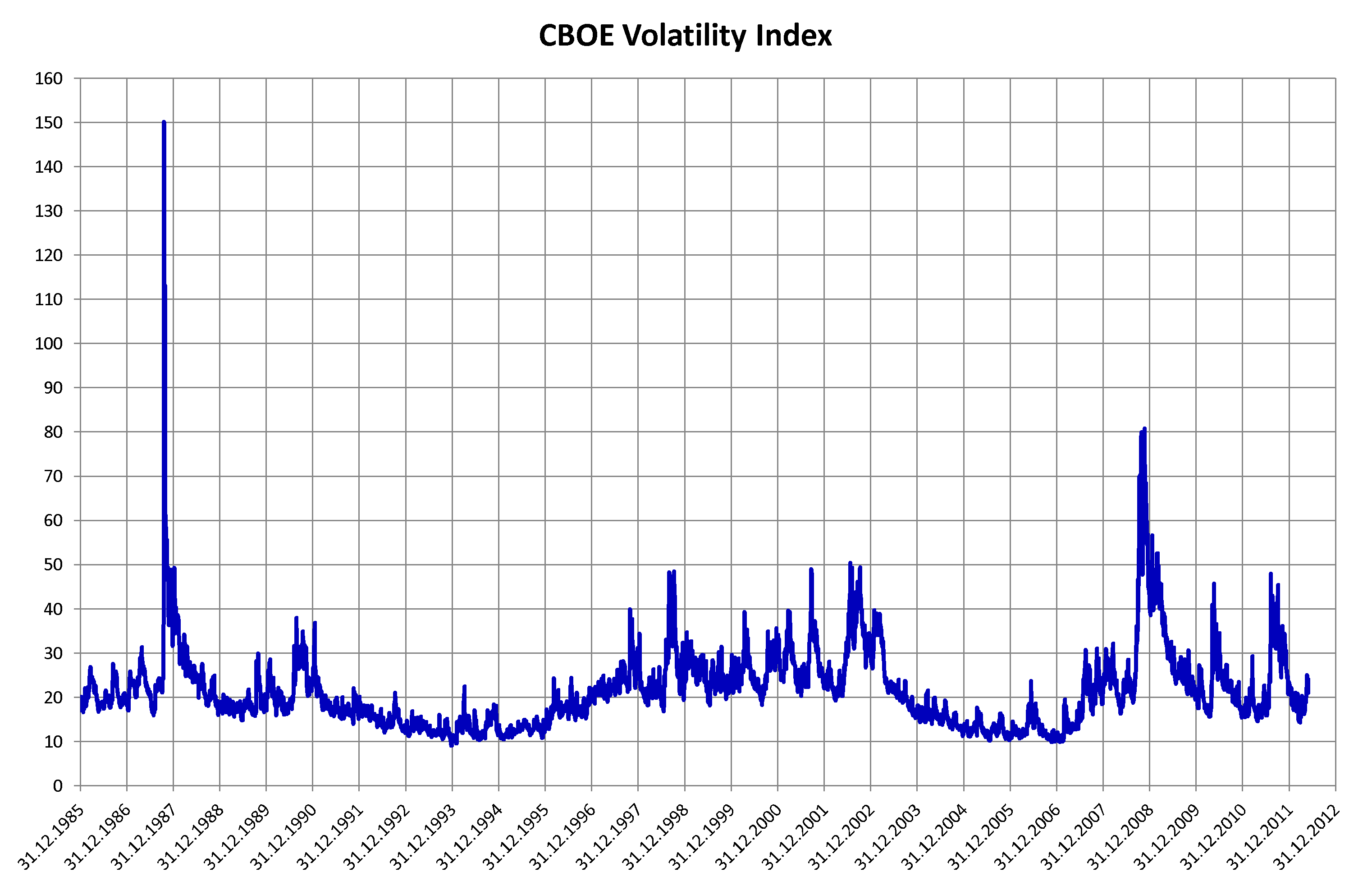
Volatility (finance)
In finance, volatility (usually denoted by "sigma, σ") is the Variability (statistics), degree of variation of a trading price series over time, usually measured by the standard deviation of logarithmic returns. Historic volatility measures a time series of past market prices. Implied volatility looks forward in time, being derived from the market price of a market-traded derivative (in particular, an option). Volatility terminology Volatility as described here refers to the actual volatility, more specifically: * actual current volatility of a financial instrument for a specified period (for example 30 days or 90 days), based on historical prices over the specified period with the last observation the most recent price. * actual historical volatility which refers to the volatility of a financial instrument over a specified period but with the last observation on a date in the past **near synonymous is realized volatility, the square root of the realized variance, in turn c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Correlation
In statistics, correlation or dependence is any statistical relationship, whether causal or not, between two random variables or bivariate data. Although in the broadest sense, "correlation" may indicate any type of association, in statistics it usually refers to the degree to which a pair of variables are '' linearly'' related. Familiar examples of dependent phenomena include the correlation between the height of parents and their offspring, and the correlation between the price of a good and the quantity the consumers are willing to purchase, as it is depicted in the demand curve. Correlations are useful because they can indicate a predictive relationship that can be exploited in practice. For example, an electrical utility may produce less power on a mild day based on the correlation between electricity demand and weather. In this example, there is a causal relationship, because extreme weather causes people to use more electricity for heating or cooling. However, in g ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Standard Deviation
In statistics, the standard deviation is a measure of the amount of variation of the values of a variable about its Expected value, mean. A low standard Deviation (statistics), deviation indicates that the values tend to be close to the mean (also called the expected value) of the set, while a high standard deviation indicates that the values are spread out over a wider range. The standard deviation is commonly used in the determination of what constitutes an outlier and what does not. Standard deviation may be abbreviated SD or std dev, and is most commonly represented in mathematical texts and equations by the lowercase Greek alphabet, Greek letter Sigma, σ (sigma), for the population standard deviation, or the Latin script, Latin letter ''s'', for the sample standard deviation. The standard deviation of a random variable, Sample (statistics), sample, statistical population, data set, or probability distribution is the square root of its variance. (For a finite population, v ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Variance
In probability theory and statistics, variance is the expected value of the squared deviation from the mean of a random variable. The standard deviation (SD) is obtained as the square root of the variance. Variance is a measure of dispersion, meaning it is a measure of how far a set of numbers is spread out from their average value. It is the second central moment of a distribution, and the covariance of the random variable with itself, and it is often represented by \sigma^2, s^2, \operatorname(X), V(X), or \mathbb(X). An advantage of variance as a measure of dispersion is that it is more amenable to algebraic manipulation than other measures of dispersion such as the expected absolute deviation; for example, the variance of a sum of uncorrelated random variables is equal to the sum of their variances. A disadvantage of the variance for practical applications is that, unlike the standard deviation, its units differ from the random variable, which is why the standard devi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Covariance
In probability theory and statistics, covariance is a measure of the joint variability of two random variables. The sign of the covariance, therefore, shows the tendency in the linear relationship between the variables. If greater values of one variable mainly correspond with greater values of the other variable, and the same holds for lesser values (that is, the variables tend to show similar behavior), the covariance is positive. In the opposite case, when greater values of one variable mainly correspond to lesser values of the other (that is, the variables tend to show opposite behavior), the covariance is negative. The magnitude of the covariance is the geometric mean of the variances that are in common for the two random variables. The Pearson product-moment correlation coefficient, correlation coefficient normalizes the covariance by dividing by the geometric mean of the total variances for the two random variables. A distinction must be made between (1) the covariance of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ordinary Least Squares
In statistics, ordinary least squares (OLS) is a type of linear least squares method for choosing the unknown parameters in a linear regression In statistics, linear regression is a statistical model, model that estimates the relationship between a Scalar (mathematics), scalar response (dependent variable) and one or more explanatory variables (regressor or independent variable). A mode ... model (with fixed level-one effects of a linear function of a set of explanatory variables) by the principle of least squares: minimizing the sum of the squares of the differences between the observed dependent variable (values of the variable being observed) in the input dataset and the output of the (linear) function of the independent variable. Some sources consider OLS to be linear regression. Geometrically, this is seen as the sum of the squared distances, parallel to the axis of the dependent variable, between each data point in the set and the corresponding point on the regression ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alpha (finance)
Alpha is a measure of the active return on an investment, the performance of that investment compared with a suitable market index. An alpha of 1% means the investment's return on investment over a selected period of time was 1% better than the market during that same period; a negative alpha means the investment underperformed the market. Alpha, along with beta, is one of two key coefficients in the capital asset pricing model used in modern portfolio theory and is closely related to other important quantities such as standard deviation, R-squared and the Sharpe ratio. In modern financial markets, where index funds are widely available for purchase, alpha is commonly used to judge the performance of mutual funds and similar investments. As these funds include various fees normally expressed in percent terms, the fund has to maintain an alpha greater than its fees in order to provide positive gains compared with an index fund. Historically, the vast majority of traditional fun ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |