Radioactive on:
[Wikipedia]
[Google]
[Amazon]
 Radioactive decay (also known as nuclear decay, radioactivity, radioactive disintegration, or nuclear disintegration) is the process by which an unstable
Radioactive decay (also known as nuclear decay, radioactivity, radioactive disintegration, or nuclear disintegration) is the process by which an unstable
 Radioactivity was discovered in 1896 by scientists
Radioactivity was discovered in 1896 by scientists
 The dangers of ionizing radiation due to radioactivity and X-rays were not immediately recognized.
The dangers of ionizing radiation due to radioactivity and X-rays were not immediately recognized.
 However, the biological effects of radiation due to radioactive substances were less easy to gauge. This gave the opportunity for many physicians and corporations to market radioactive substances as patent medicines. Examples were radium
However, the biological effects of radiation due to radioactive substances were less easy to gauge. This gave the opportunity for many physicians and corporations to market radioactive substances as patent medicines. Examples were radium
 The International System of Units (SI) unit of radioactive activity is the
The International System of Units (SI) unit of radioactive activity is the
 Early researchers found that an
Early researchers found that an  In analysing the nature of the decay products, it was obvious from the direction of the
In analysing the nature of the decay products, it was obvious from the direction of the

 A number of experiments have found that decay rates of other modes of artificial and naturally occurring radioisotopes are, to a high degree of precision, unaffected by external conditions such as temperature, pressure, the chemical environment, and electric, magnetic, or gravitational fields. Comparison of laboratory experiments over the last century, studies of the Oklo natural nuclear reactor (which exemplified the effects of thermal neutrons on nuclear decay), and astrophysical observations of the luminosity decays of distant supernovae (which occurred far away so the light has taken a great deal of time to reach us), for example, strongly indicate that unperturbed decay rates have been constant (at least to within the limitations of small experimental errors) as a function of time as well.
Recent results suggest the possibility that decay rates might have a weak dependence on environmental factors. It has been suggested that measurements of decay rates of silicon-32, manganese-54, and radium-226 exhibit small seasonal variations (of the order of 0.1%). However, such measurements are highly susceptible to systematic errors, and a subsequent paper has found no evidence for such correlations in seven other isotopes (22Na, 44Ti, 108Ag, 121Sn, 133Ba, 241Am, 238Pu), and sets upper limits on the size of any such effects. The decay of
A number of experiments have found that decay rates of other modes of artificial and naturally occurring radioisotopes are, to a high degree of precision, unaffected by external conditions such as temperature, pressure, the chemical environment, and electric, magnetic, or gravitational fields. Comparison of laboratory experiments over the last century, studies of the Oklo natural nuclear reactor (which exemplified the effects of thermal neutrons on nuclear decay), and astrophysical observations of the luminosity decays of distant supernovae (which occurred far away so the light has taken a great deal of time to reach us), for example, strongly indicate that unperturbed decay rates have been constant (at least to within the limitations of small experimental errors) as a function of time as well.
Recent results suggest the possibility that decay rates might have a weak dependence on environmental factors. It has been suggested that measurements of decay rates of silicon-32, manganese-54, and radium-226 exhibit small seasonal variations (of the order of 0.1%). However, such measurements are highly susceptible to systematic errors, and a subsequent paper has found no evidence for such correlations in seven other isotopes (22Na, 44Ti, 108Ag, 121Sn, 133Ba, 241Am, 238Pu), and sets upper limits on the size of any such effects. The decay of
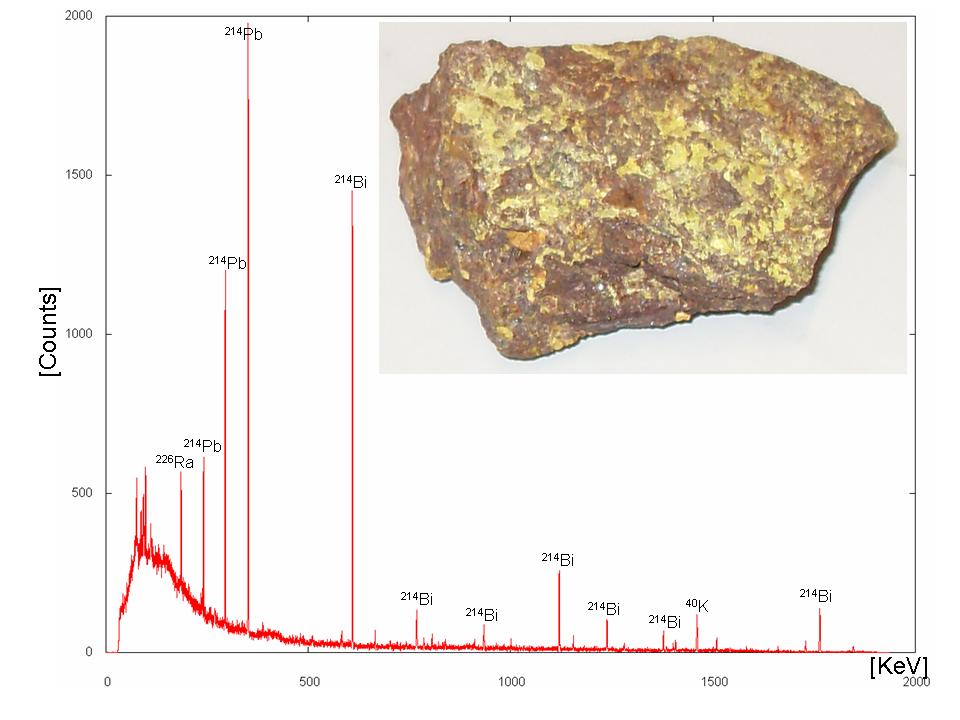 An example is the natural decay chain of 238U:
* Uranium-238 decays, through alpha-emission, with a half-life of billion years to thorium-234
* which decays, through beta-emission, with a half-life of days to protactinium-234m
* which decays, through beta-emission, with a half-life of minutes to
An example is the natural decay chain of 238U:
* Uranium-238 decays, through alpha-emission, with a half-life of billion years to thorium-234
* which decays, through beta-emission, with a half-life of days to protactinium-234m
* which decays, through beta-emission, with a half-life of minutes to
file:Radioactive.svg, The trefoil symbol used to warn of presence of radioactive material or ionising radiation
File:Logo iso radiation.svg, 2007 ISO radioactivity hazard symbol intended for IAEA Category 1, 2 and 3 sources defined as dangerous sources capable of death or serious injuryIAEA news release Feb 2007
/ref> File:Dangclass7.svg, The dangerous goods transport classification sign for radioactive materials
"Radioactivity"
Encyclopædia Britannica. 2006.
The Lund/LBNL Nuclear Data Search
– Contains tabulated information on radioactive decay types and energies.
Nomenclature of nuclear chemistry
The Live Chart of Nuclides – IAEA
Interactive Chart of Nuclides
Health Physics Society Public Education Website
*
Annotated bibliography for radioactivity from the Alsos Digital Library for Nuclear Issues
by Wolfgang Bauer
by David M. Harrison * "Henri Becquerel: The Discovery of Radioactivity", Becquerel's 1896 articles online and analyzed on
BibNum
' lick 'à télécharger' for English version/small>. * "Radioactive change", Rutherford & Soddy article (1903), online and analyzed on
Bibnum
' lick 'à télécharger' for English version/small>. {{DEFAULTSORT:Radioactive Decay Exponentials Poisson point processes
atomic nucleus
The atomic nucleus is the small, dense region consisting of protons and neutrons at the center of an atom, discovered in 1911 by Ernest Rutherford based on the 1909 Geiger–Marsden gold foil experiment. After the discovery of the neutron ...
loses energy by radiation. A material containing unstable nuclei is considered radioactive. Three of the most common types of decay are alpha decay ( ), beta decay ( ), and gamma decay ( ), all of which involve emitting one or more particle
In the physical sciences, a particle (or corpuscule in older texts) is a small localized object which can be described by several physical or chemical properties, such as volume, density, or mass.
They vary greatly in size or quantity, from ...
s. The weak force
Weak may refer to:
Songs
* Weak (AJR song), "Weak" (AJR song), 2016
* Weak (Melanie C song), "Weak" (Melanie C song), 2011
* Weak (SWV song), "Weak" (SWV song), 1993
* Weak (Skunk Anansie song), "Weak" (Skunk Anansie song), 1995
* "Weak", a song ...
is the mechanism that is responsible for beta decay, while the other two are governed by the electromagnetism
In physics, electromagnetism is an interaction that occurs between particles with electric charge. It is the second-strongest of the four fundamental interactions, after the strong force, and it is the dominant force in the interactions of ...
and nuclear force
The nuclear force (or nucleon–nucleon interaction, residual strong force, or, historically, strong nuclear force) is a force that acts between the protons and neutrons of atoms. Neutrons and protons, both nucleons, are affected by the nucle ...
. A fourth type of common decay is electron capture, in which an unstable nucleus captures an inner electron from one of the electron shell
In chemistry and atomic physics, an electron shell may be thought of as an orbit followed by electrons around an atom's nucleus. The closest shell to the nucleus is called the "1 shell" (also called the "K shell"), followed by the "2 shell" (or ...
s. The loss of that electron from the shell results in a cascade of electrons dropping down to that lower shell resulting in emission of discrete X-rays from the transitions. A common example is iodine-125 commonly used in medical settings.
Radioactive decay is a stochastic (i.e. random) process at the level of single atoms. According to quantum theory, it is impossible to predict when a particular atom will decay, regardless of how long the atom has existed. However, for a significant number of identical atoms, the overall decay rate can be expressed as a decay constant or as half-life. The half-lives of radioactive atoms have a huge range; from nearly instantaneous to far longer than the age of the universe
In physical cosmology, the age of the universe is the time elapsed since the Big Bang. Astronomers have derived two different measurements of the age of the universe:
a measurement based on direct observations of an early state of the universe, ...
.
The decaying nucleus is called the ''parent radionuclide'' (or ''parent radioisotope''Radionuclide is the more correct term, but radioisotope is also used. The difference between isotope and nuclide is explained at .), and the process produces at least one ''daughter nuclide
In nuclear physics, a decay product (also known as a daughter product, daughter isotope, radio-daughter, or daughter nuclide) is the remaining nuclide left over from radioactive decay. Radioactive decay often proceeds via a sequence of steps (de ...
''. Except for gamma decay or internal conversion from a nuclear excited state, the decay is a nuclear transmutation resulting in a daughter containing a different number of protons or neutron
The neutron is a subatomic particle, symbol or , which has a neutral (not positive or negative) charge, and a mass slightly greater than that of a proton. Protons and neutrons constitute the nuclei of atoms. Since protons and neutrons beh ...
s (or both). When the number of protons changes, an atom of a different chemical element
A chemical element is a species of atoms that have a given number of protons in their nuclei, including the pure substance consisting only of that species. Unlike chemical compounds, chemical elements cannot be broken down into simpler sub ...
is created.
* Alpha decay occurs when the nucleus ejects an alpha particle
Alpha particles, also called alpha rays or alpha radiation, consist of two protons and two neutrons bound together into a particle identical to a helium-4 nucleus. They are generally produced in the process of alpha decay, but may also be pr ...
(helium nucleus).
* Beta decay
In nuclear physics, beta decay (β-decay) is a type of radioactive decay in which a beta particle (fast energetic electron or positron) is emitted from an atomic nucleus, transforming the original nuclide to an isobar of that nuclide. For ...
occurs in two ways;
* In gamma decay a radioactive nucleus first decays by the emission of an alpha or beta particle. The daughter nucleus that results is usually left in an excited state and it can decay to a lower energy state by emitting a gamma ray photon.
* In neutron emission
Neutron emission is a mode of radioactive decay in which one or more neutrons are ejected from a nucleus. It occurs in the most neutron-rich/proton-deficient nuclides, and also from excited states of other nuclides as in photoneutron emission and ...
, extremely neutron-rich nuclei, formed due to other types of decay or after many successive neutron captures, occasionally lose energy by way of neutron emission, resulting in a change from one isotope
Isotopes are two or more types of atoms that have the same atomic number (number of protons in their nuclei) and position in the periodic table (and hence belong to the same chemical element), and that differ in nucleon numbers (mass numb ...
to another of the same element.
* In electron capture, the nucleus may capture an orbiting electron, causing a proton to convert into a neutron. A neutrino and a gamma ray are subsequently emitted.
* In cluster decay and nuclear fission, a nucleus heavier than an alpha particle is emitted.
By contrast there are radioactive decay processes that do not result in a nuclear transmutation. The energy of an excited nucleus may be emitted as a gamma ray in a process called gamma decay, or that energy may be lost when the nucleus interacts with an orbital electron causing its ejection from the atom, in a process called internal conversion
Internal conversion is a non-radioactive, atomic decay process where an excited nucleus interacts electromagnetically with one of the orbital electrons of an atom. This causes the electron to be emitted (ejected) from the atom. Thus, in internal ...
. Another type of radioactive decay results in products that vary, appearing as two or more "fragments" of the original nucleus with a range of possible masses. This decay, called spontaneous fission, happens when a large unstable nucleus spontaneously splits into two (or occasionally three) smaller daughter nuclei, and generally leads to the emission of gamma rays, neutrons, or other particles from those products.
In contrast, decay products from a nucleus ''with spin'' may be distributed ''non-isotropically'' with respect to that spin direction. Either because of an external influence such as an electromagnetic field, or because the nucleus was produced in a dynamic process that constrained the direction of its spin, the anisotropy
Anisotropy () is the property of a material which allows it to change or assume different properties in different directions, as opposed to isotropy. It can be defined as a difference, when measured along different axes, in a material's physic ...
may be detectable. Such a parent process could be a previous decay, or a nuclear reaction
In nuclear physics and nuclear chemistry, a nuclear reaction is a process in which two nuclei, or a nucleus and an external subatomic particle, collide to produce one or more new nuclides. Thus, a nuclear reaction must cause a transformatio ...
.See Wu experiment
The Wu experiment was a particle and nuclear physics experiment conducted in 1956 by the Chinese American physicist Chien-Shiung Wu in collaboration with the Low Temperature Group of the US National Bureau of Standards.
The experiment's pur ...
among other counterexamples when the decaying atom is influenced by external factors.
For a summary table showing the number of stable and radioactive nuclides, see radionuclide. There are 28 naturally occurring chemical elements on Earth that are radioactive, consisting of 34 radionuclides (6 elements have 2 different radionuclides) that date before the time of formation of the Solar System
The Solar System Capitalization of the name varies. The International Astronomical Union, the authoritative body regarding astronomical nomenclature, specifies capitalizing the names of all individual astronomical objects but uses mixed "Solar ...
. These 34 are known as primordial nuclides. Well-known examples are uranium
Uranium is a chemical element with the symbol U and atomic number 92. It is a silvery-grey metal in the actinide series of the periodic table. A uranium atom has 92 protons and 92 electrons, of which 6 are valence electrons. Uranium is weak ...
and thorium, but also included are naturally occurring long-lived radioisotopes, such as potassium-40
Potassium-40 (40K) is a radioactive isotope of potassium which has a long half-life of 1.25 billion years. It makes up about 0.012% (120 ppm) of the total amount of potassium found in nature.
Potassium-40 undergoes three types of radioactive d ...
.
Another 50 or so shorter-lived radionuclides found on Earth such as radium-226 and radon-222
Radon-222 (222Rn, Rn-222, historically radium emanation or radon) is the most stable isotope of radon, with a half-life of approximately 3.8 days. It is transient in the decay chain of primordial uranium-238 and is the immediate decay product of ...
, are the products of decay chain
In nuclear science, the decay chain refers to a series of radioactive decays of different radioactive decay products as a sequential series of transformations. It is also known as a "radioactive cascade". Most radioisotopes do not decay dire ...
s that began with the primordial nuclides, or are the product of ongoing cosmogenic
Cosmogenic nuclides (or cosmogenic isotopes) are rare nuclides (isotopes) created when a high-energy cosmic ray interacts with the nucleus of an ''in situ'' Solar System atom, causing nucleons (protons and neutrons) to be expelled from the atom ...
processes, such as the production of carbon-14 from nitrogen-14 in the atmosphere by cosmic rays. Radionuclides may also be produced artificially in particle accelerators or nuclear reactors, resulting in 650 of these with half-lives of over an hour, and several thousand more with even shorter half-lives. (See List of nuclides
This list of nuclides shows observed nuclides that either are stable or, if radioactive, have half-lives longer than one hour. This represents isotopes of the first 105 elements, except for elements 87 (francium) and 102 (nobelium). At least 3,300 ...
for a list of these sorted by half-life.)
History of discovery
 Radioactivity was discovered in 1896 by scientists
Radioactivity was discovered in 1896 by scientists Henri Becquerel
Antoine Henri Becquerel (; 15 December 1852 – 25 August 1908) was a French engineer, physicist, Nobel laureate, and the first person to discover evidence of radioactivity. For work in this field he, along with Marie Skłodowska-Curie and Pie ...
and Marie Curie, while working with phosphorescent
Phosphorescence is a type of photoluminescence related to fluorescence. When exposed to light (radiation) of a shorter wavelength, a phosphorescent substance will glow, absorbing the light and reemitting it at a longer wavelength. Unlike fluor ...
materials. These materials glow in the dark after exposure to light, and he suspected that the glow produced in cathode ray tubes by X-ray
An X-ray, or, much less commonly, X-radiation, is a penetrating form of high-energy electromagnetic radiation. Most X-rays have a wavelength ranging from 10 picometers to 10 nanometers, corresponding to frequencies in the range 30&nb ...
s might be associated with phosphorescence. Becquerel wrapped a photographic plate in black paper and placed various phosphorescent salts
In chemistry, a salt is a chemical compound consisting of an ionic assembly of positively charged cations and negatively charged anions, which results in a compound with no net electric charge. A common example is table salt, with positively c ...
on it. All results were negative until he used uranium
Uranium is a chemical element with the symbol U and atomic number 92. It is a silvery-grey metal in the actinide series of the periodic table. A uranium atom has 92 protons and 92 electrons, of which 6 are valence electrons. Uranium is weak ...
salts. The uranium salts caused a blackening of the plate in spite of the plate being wrapped in black paper. These radiations were given the name "Becquerel Rays".
It soon became clear that the blackening of the plate had nothing to do with phosphorescence, as the blackening was also produced by non-phosphorescent salts
In chemistry, a salt is a chemical compound consisting of an ionic assembly of positively charged cations and negatively charged anions, which results in a compound with no net electric charge. A common example is table salt, with positively c ...
of uranium and by metallic uranium. It became clear from these experiments that there was a form of invisible radiation that could pass through paper and was causing the plate to react as if exposed to light.
At first, it seemed as though the new radiation was similar to the then recently discovered X-rays. Further research by Becquerel, Ernest Rutherford
Ernest Rutherford, 1st Baron Rutherford of Nelson, (30 August 1871 – 19 October 1937) was a New Zealand physicist who came to be known as the father of nuclear physics.
''Encyclopædia Britannica'' considers him to be the greatest ...
, Paul Villard, Pierre Curie, Marie Curie, and others showed that this form of radioactivity was significantly more complicated. Rutherford was the first to realize that all such elements decay in accordance with the same mathematical exponential formula. Rutherford and his student Frederick Soddy
Frederick Soddy FRS (2 September 1877 – 22 September 1956) was an English radiochemist who explained, with Ernest Rutherford, that radioactivity is due to the transmutation of elements, now known to involve nuclear reactions. He also prov ...
were the first to realize that many decay processes resulted in the transmutation of one element to another. Subsequently, the radioactive displacement law of Fajans and Soddy was formulated to describe the products of alpha and beta decay
In nuclear physics, beta decay (β-decay) is a type of radioactive decay in which a beta particle (fast energetic electron or positron) is emitted from an atomic nucleus, transforming the original nuclide to an isobar of that nuclide. For ...
.
The early researchers also discovered that many other chemical element
A chemical element is a species of atoms that have a given number of protons in their nuclei, including the pure substance consisting only of that species. Unlike chemical compounds, chemical elements cannot be broken down into simpler sub ...
s, besides uranium, have radioactive isotopes
A radionuclide (radioactive nuclide, radioisotope or radioactive isotope) is a nuclide that has excess nuclear energy, making it unstable. This excess energy can be used in one of three ways: emitted from the nucleus as gamma radiation; transferr ...
. A systematic search for the total radioactivity in uranium ores also guided Pierre and Marie Curie to isolate two new elements: polonium
Polonium is a chemical element with the symbol Po and atomic number 84. Polonium is a chalcogen. A rare and highly radioactive metal with no stable isotopes, polonium is chemically similar to selenium and tellurium, though its metallic character ...
and radium
Radium is a chemical element with the symbol Ra and atomic number 88. It is the sixth element in group 2 of the periodic table, also known as the alkaline earth metals. Pure radium is silvery-white, but it readily reacts with nitrogen (rathe ...
. Except for the radioactivity of radium, the chemical similarity of radium to barium made these two elements difficult to distinguish.
Marie and Pierre Curie's study of radioactivity is an important factor in science and medicine. After their research on Becquerel's rays led them to the discovery of both radium and polonium, they coined the term "radioactivity" to define the emission of ionizing radiation by some heavy elements. (Later the term was generalized to all elements.) Their research on the penetrating rays in uranium and the discovery of radium launched an era of using radium for the treatment of cancer. Their exploration of radium could be seen as the first peaceful use of nuclear energy and the start of modern nuclear medicine
Nuclear medicine or nucleology is a medical specialty involving the application of radioactive substances in the diagnosis and treatment of disease. Nuclear imaging, in a sense, is " radiology done inside out" because it records radiation emi ...
.
Early health dangers
 The dangers of ionizing radiation due to radioactivity and X-rays were not immediately recognized.
The dangers of ionizing radiation due to radioactivity and X-rays were not immediately recognized.
X-rays
The discovery of X‑rays by Wilhelm Röntgen in 1895 led to widespread experimentation by scientists, physicians, and inventors. Many people began recounting stories of burns, hair loss and worse in technical journals as early as 1896. In February of that year, Professor Daniel and Dr. Dudley ofVanderbilt University
Vanderbilt University (informally Vandy or VU) is a private research university in Nashville, Tennessee. Founded in 1873, it was named in honor of shipping and rail magnate Cornelius Vanderbilt, who provided the school its initial $1-million ...
performed an experiment involving X-raying Dudley's head that resulted in his hair loss. A report by Dr. H.D. Hawks, of his suffering severe hand and chest burns in an X-ray demonstration, was the first of many other reports in ''Electrical Review''.
Other experimenters, including Elihu Thomson
Elihu Thomson (March 29, 1853 – March 13, 1937) was an English-born American engineer and inventor who was instrumental in the founding of major electrical companies in the United States, the United Kingdom and France.
Early life
He was bor ...
and Nikola Tesla, also reported burns. Thomson deliberately exposed a finger to an X-ray tube over a period of time and suffered pain, swelling, and blistering. Other effects, including ultraviolet rays and ozone, were sometimes blamed for the damage, and many physicians still claimed that there were no effects from X-ray exposure at all.
Despite this, there were some early systematic hazard investigations, and as early as 1902 William Herbert Rollins wrote almost despairingly that his warnings about the dangers involved in the careless use of X-rays were not being heeded, either by industry or by his colleagues. By this time, Rollins had proved that X-rays could kill experimental animals, could cause a pregnant guinea pig to abort, and that they could kill a foetus. He also stressed that "animals vary in susceptibility to the external action of X-light" and warned that these differences be considered when patients were treated by means of X-rays.
Radioactive substances
enema
An enema, also known as a clyster, is an injection of fluid into the lower bowel by way of the rectum.Cullingworth, ''A Manual of Nursing, Medical and Surgical'':155 The word enema can also refer to the liquid injected, as well as to a device ...
treatments, and radium-containing waters to be drunk as tonics. Marie Curie protested against this sort of treatment, warning that "radium is dangerous in untrained hands." Curie later died from aplastic anaemia
Aplastic anemia is a cancer in which the body fails to make blood cells in sufficient numbers. Blood cells are produced in the bone marrow by stem cells that reside there. Aplastic anemia causes a deficiency of all blood cell types: red blood c ...
, likely caused by exposure to ionizing radiation. By the 1930s, after a number of cases of bone necrosis and death of radium treatment enthusiasts, radium-containing medicinal products had been largely removed from the market ( radioactive quackery).
Radiation protection
Only a year after Röntgen's discovery of X rays, the American engineer Wolfram Fuchs (1896) gave what is probably the first protection advice, but it was not until 1925 that the first International Congress of Radiology (ICR) was held and considered establishing international protection standards. The effects of radiation on genes, including the effect of cancer risk, were recognized much later. In 1927, Hermann Joseph Muller published research showing genetic effects and, in 1946, was awarded the Nobel Prize in Physiology or Medicine for his findings. The second ICR was held in Stockholm in 1928 and proposed the adoption of the röntgen unit, and the International X-ray and Radium Protection Committee (IXRPC) was formed. Rolf Sievert was named Chairman, but a driving force was George Kaye of the British National Physical Laboratory. The committee met in 1931, 1934, and 1937. AfterWorld War II
World War II or the Second World War, often abbreviated as WWII or WW2, was a world war that lasted from 1939 to 1945. It involved the vast majority of the world's countries—including all of the great powers—forming two opposing ...
, the increased range and quantity of radioactive substances being handled as a result of military and civil nuclear programs led to large groups of occupational workers and the public being potentially exposed to harmful levels of ionising radiation. This was considered at the first post-war ICR convened in London in 1950, when the present International Commission on Radiological Protection
The International Commission on Radiological Protection (ICRP) is an independent, international, non-governmental organization, with the mission to protect people, animals, and the environment from the harmful effects of ionising radiation. Its r ...
(ICRP) was born.
Since then the ICRP has developed the present international system of radiation protection, covering all aspects of radiation hazards.
In 2020, Hauptmann and other 15 international researchers of eight nations, among which: Institutes of Biostatistics, Registry Research, Centers of Cancer Epidemiology, Radiation Epidemiology, and then also U.S. National Cancer Institute (NCI), International Agency for Research on Cancer (IARC) and Radiation Effects Research Foundation of Hiroshima studied definitively through meta-analysis the damage resulting from the "low doses" that have afflicted the populations of survivors of the atomic bombings of Hiroshima and Nagasaki and also in numerous accidents of nuclear plants that have occurred in the world. These scientists reported, in JNCI Monographs: Epidemiological Studies of Low Dose Ionizing Radiation and Cancer Risk, that the new epidemiological studies directly support excess cancer risks from low-dose ionizing radiation. In 2021, Italian researcher Venturi reported the first correlations between radio-caesium and pancreatic cancer with the role of caesium in biology and in pancreatitis and in diabetes of pancreatic origin.
Units
 The International System of Units (SI) unit of radioactive activity is the
The International System of Units (SI) unit of radioactive activity is the becquerel
The becquerel (; symbol: Bq) is the unit of radioactivity in the International System of Units (SI). One becquerel is defined as the activity of a quantity of radioactive material in which one nucleus decays per second. For applications relatin ...
(Bq), named in honor of the scientist Henri Becquerel
Antoine Henri Becquerel (; 15 December 1852 – 25 August 1908) was a French engineer, physicist, Nobel laureate, and the first person to discover evidence of radioactivity. For work in this field he, along with Marie Skłodowska-Curie and Pie ...
. One Bq is defined as one transformation (or decay or disintegration) per second.
An older unit of radioactivity is the curie, Ci, which was originally defined as "the quantity or mass of radium emanation in equilibrium with one gram of radium
Radium is a chemical element with the symbol Ra and atomic number 88. It is the sixth element in group 2 of the periodic table, also known as the alkaline earth metals. Pure radium is silvery-white, but it readily reacts with nitrogen (rathe ...
(element)". Today, the curie is defined as disintegrations per second, so that 1 curie (Ci) = .
For radiological protection purposes, although the United States Nuclear Regulatory Commission permits the use of the unit curie alongside SI units, the European Union
The European Union (EU) is a supranational political and economic union of member states that are located primarily in Europe. The union has a total area of and an estimated total population of about 447million. The EU has often been de ...
European units of measurement directives required that its use for "public health ... purposes" be phased out by 31 December 1985.
The effects of ionizing radiation are often measured in units of gray for mechanical or sievert
The sievert (symbol: SvNot be confused with the sverdrup or the svedberg, two non-SI units that sometimes use the same symbol.) is a unit in the International System of Units (SI) intended to represent the stochastic health risk of ionizing rad ...
for damage to tissue.
Types
electric
Electricity is the set of physical phenomena associated with the presence and motion of matter that has a property of electric charge. Electricity is related to magnetism, both being part of the phenomenon of electromagnetism, as described by ...
or magnetic field could split radioactive emissions into three types of beams. The rays were given the names alpha, beta, and gamma, in increasing order of their ability to penetrate matter. Alpha decay is observed only in heavier elements of atomic number 52 ( tellurium) and greater, with the exception of beryllium-8
Beryllium-8 (8Be, Be-8) is a radionuclide with 4 neutrons and 4 protons. It is an unbound resonance and nominally an isotope of beryllium. It decays into two alpha particles with a half-life on the order of 8.19 seconds. This has important r ...
(which decays to two alpha particles). The other two types of decay are observed in all the elements. Lead, atomic number
The atomic number or nuclear charge number (symbol ''Z'') of a chemical element is the charge number of an atomic nucleus. For ordinary nuclei, this is equal to the proton number (''n''p) or the number of protons found in the nucleus of every ...
82, is the heaviest element to have any isotopes stable (to the limit of measurement) to radioactive decay. Radioactive decay is seen in all isotopes of all elements of atomic number 83 (bismuth
Bismuth is a chemical element with the symbol Bi and atomic number 83. It is a post-transition metal and one of the pnictogens, with chemical properties resembling its lighter group 15 siblings arsenic and antimony. Elemental bismuth occurs ...
) or greater. Bismuth-209
Bismuth-209 (209Bi) is the isotope of bismuth with the longest known half-life of any radioisotope that undergoes α-decay (alpha decay). It has 83 protons and a magic number of 126 neutrons, and an atomic mass of 208.9803987 amu (atomic mass un ...
, however, is only very slightly radioactive, with a half-life greater than the age of the universe; radioisotopes with extremely long half-lives are considered effectively stable for practical purposes.
electromagnetic force
In physics, electromagnetism is an interaction that occurs between particles with electric charge. It is the second-strongest of the four fundamental interactions, after the strong force, and it is the dominant force in the interactions o ...
s applied to the radiations by external magnetic and electric fields that alpha particle
Alpha particles, also called alpha rays or alpha radiation, consist of two protons and two neutrons bound together into a particle identical to a helium-4 nucleus. They are generally produced in the process of alpha decay, but may also be pr ...
s carried a positive charge, beta particles carried a negative charge, and gamma rays were neutral. From the magnitude of deflection, it was clear that alpha particles were much more massive than beta particles. Passing alpha particles through a very thin glass window and trapping them in a discharge tube
A gas-filled tube, also commonly known as a discharge tube or formerly as a Plücker tube, is an arrangement of electrodes in a gas within an insulating, temperature-resistant envelope. Gas-filled tubes exploit phenomena related to electric ...
allowed researchers to study the emission spectrum of the captured particles, and ultimately proved that alpha particles are helium
Helium (from el, ἥλιος, helios, lit=sun) is a chemical element with the symbol He and atomic number 2. It is a colorless, odorless, tasteless, non-toxic, inert, monatomic gas and the first in the noble gas group in the periodic table. ...
nuclei. Other experiments showed beta radiation, resulting from decay and cathode ray
Cathode rays or electron beam (e-beam) are streams of electrons observed in discharge tubes. If an evacuated glass tube is equipped with two electrodes and a voltage is applied, glass behind the positive electrode is observed to glow, due to el ...
s, were high-speed electrons
The electron ( or ) is a subatomic particle with a negative one elementary electric charge. Electrons belong to the first generation of the lepton particle family,
and are generally thought to be elementary particles because they have no ...
. Likewise, gamma radiation and X-rays were found to be high-energy electromagnetic radiation.
The relationship between the types of decays also began to be examined: For example, gamma decay was almost always found to be associated with other types of decay, and occurred at about the same time, or afterwards. Gamma decay as a separate phenomenon, with its own half-life (now termed isomeric transition), was found in natural radioactivity to be a result of the gamma decay of excited metastable nuclear isomer
A nuclear isomer is a metastable state of an atomic nucleus, in which one or more nucleons (protons or neutrons) occupy higher energy levels than in the ground state of the same nucleus. "Metastable" describes nuclei whose excited states have ...
s, which were in turn created from other types of decay.
Although alpha, beta, and gamma radiations were most commonly found, other types of emission were eventually discovered. Shortly after the discovery of the positron in cosmic ray products, it was realized that the same process that operates in classical beta decay
In nuclear physics, beta decay (β-decay) is a type of radioactive decay in which a beta particle (fast energetic electron or positron) is emitted from an atomic nucleus, transforming the original nuclide to an isobar of that nuclide. For ...
can also produce positrons (positron emission
Positron emission, beta plus decay, or β+ decay is a subtype of radioactive decay called beta decay, in which a proton inside a radionuclide nucleus is converted into a neutron while releasing a positron and an electron neutrino (). Positron ...
), along with neutrino
A neutrino ( ; denoted by the Greek letter ) is a fermion (an elementary particle with spin of ) that interacts only via the weak interaction and gravity. The neutrino is so named because it is electrically neutral and because its rest mass ...
s (classical beta decay produces antineutrinos). In a more common analogous process, called electron capture, some proton-rich nuclides were found to capture their own atomic electrons instead of emitting positrons, and subsequently, these nuclides emit only a neutrino and a gamma ray from the excited nucleus (and often also Auger electron
The Auger effect or Auger−Meitner effect is a physical phenomenon in which the filling of an inner-shell vacancy of an atom is accompanied by the emission of an electron from the same atom. When a core electron is removed, leaving a vacancy, ...
s and characteristic X-rays, as a result of the re-ordering of electrons to fill the place of the missing captured electron). These types of decay involve the nuclear capture of electrons or emission of electrons or positrons, and thus acts to move a nucleus toward the ratio of neutrons to protons that has the least energy for a given total number of nucleon
In physics and chemistry, a nucleon is either a proton or a neutron, considered in its role as a component of an atomic nucleus. The number of nucleons in a nucleus defines the atom's mass number (nucleon number).
Until the 1960s, nucleons were ...
s. This consequently produces a more stable (lower energy) nucleus.
A hypothetical process of positron capture, analogous to electron capture, is theoretically possible in antimatter atoms, but has not been observed, as complex antimatter atoms beyond antihelium
In modern physics, antimatter is defined as matter composed of the antiparticles (or "partners") of the corresponding particles in "ordinary" matter. Antimatter occurs in natural processes like cosmic ray collisions and some types of radioact ...
are not experimentally available. Such a decay would require antimatter atoms at least as complex as beryllium-7, which is the lightest known isotope of normal matter to undergo decay by electron capture.
Shortly after the discovery of the neutron
The neutron is a subatomic particle, symbol or , which has a neutral (not positive or negative) charge, and a mass slightly greater than that of a proton. Protons and neutrons constitute the nuclei of atoms. Since protons and neutrons beh ...
in 1932, Enrico Fermi realized that certain rare beta-decay reactions immediately yield neutrons as an additional decay particle, so called beta-delayed neutron emission
Neutron emission is a mode of radioactive decay in which one or more neutrons are ejected from a nucleus. It occurs in the most neutron-rich/proton-deficient nuclides, and also from excited states of other nuclides as in photoneutron emission and ...
. Neutron emission usually happens from nuclei that are in an excited state, such as the excited 17O* produced from the beta decay of 17N. The neutron emission process itself is controlled by the nuclear force
The nuclear force (or nucleon–nucleon interaction, residual strong force, or, historically, strong nuclear force) is a force that acts between the protons and neutrons of atoms. Neutrons and protons, both nucleons, are affected by the nucle ...
and therefore is extremely fast, sometimes referred to as "nearly instantaneous". Isolated proton emission
Proton emission (also known as proton radioactivity) is a rare type of radioactive decay in which a proton is ejected from a nucleus. Proton emission can occur from high-lying excited states in a nucleus following a beta decay, in which case t ...
was eventually observed in some elements. It was also found that some heavy elements may undergo spontaneous fission into products that vary in composition. In a phenomenon called cluster decay, specific combinations of neutrons and protons other than alpha particles (helium nuclei) were found to be spontaneously emitted from atoms.
Other types of radioactive decay were found to emit previously seen particles but via different mechanisms. An example is internal conversion
Internal conversion is a non-radioactive, atomic decay process where an excited nucleus interacts electromagnetically with one of the orbital electrons of an atom. This causes the electron to be emitted (ejected) from the atom. Thus, in internal ...
, which results in an initial electron emission, and then often further characteristic X-rays and Auger electron
The Auger effect or Auger−Meitner effect is a physical phenomenon in which the filling of an inner-shell vacancy of an atom is accompanied by the emission of an electron from the same atom. When a core electron is removed, leaving a vacancy, ...
s emissions, although the internal conversion process involves neither beta nor gamma decay. A neutrino is not emitted, and none of the electron(s) and photon(s) emitted originate in the nucleus, even though the energy to emit all of them does originate there. Internal conversion decay, like isomeric transition gamma decay and neutron emission, involves the release of energy by an excited nuclide, without the transmutation of one element into another.
Rare events that involve a combination of two beta-decay-type events happening simultaneously are known (see below). Any decay process that does not violate the conservation of energy or momentum laws (and perhaps other particle conservation laws) is permitted to happen, although not all have been detected. An interesting example discussed in a final section, is bound state beta decay of rhenium-187. In this process, the beta electron-decay of the parent nuclide is not accompanied by beta electron emission, because the beta particle has been captured into the K-shell of the emitting atom. An antineutrino is emitted, as in all negative beta decays.
Radionuclides can undergo a number of different reactions. These are summarized in the following table. A nucleus with mass number
The mass number (symbol ''A'', from the German word ''Atomgewicht'' tomic weight, also called atomic mass number or nucleon number, is the total number of protons and neutrons (together known as nucleons) in an atomic nucleus. It is approxima ...
''A'' and atomic number
The atomic number or nuclear charge number (symbol ''Z'') of a chemical element is the charge number of an atomic nucleus. For ordinary nuclei, this is equal to the proton number (''n''p) or the number of protons found in the nucleus of every ...
''Z'' is represented as (''A'', ''Z''). The column "Daughter nucleus" indicates the difference between the new nucleus and the original nucleus. Thus, (''A'' − 1, ''Z'') means that the mass number is one less than before, but the atomic number is the same as before.
If energy circumstances are favorable, a given radionuclide may undergo many competing types of decay, with some atoms decaying by one route, and others decaying by another. An example is copper-64
Copper-64 (64Cu) is a positron and beta emitting isotope of copper, with applications for molecular radiotherapy and positron emission tomography. Its unusually long half-life (12.7-hours) for a positron-emitting isotope makes it increasingly us ...
, which has 29 protons, and 35 neutrons, which decays with a half-life of hours. This isotope has one unpaired proton and one unpaired neutron, so either the proton or the neutron can decay to the other particle, which has opposite isospin
In nuclear physics and particle physics, isospin (''I'') is a quantum number related to the up- and down quark content of the particle. More specifically, isospin symmetry is a subset of the flavour symmetry seen more broadly in the interactions ...
. This particular nuclide (though not all nuclides in this situation) is more likely to decay through beta plus decay (%) than through electron capture (%). The excited energy states resulting from these decays which fail to end in a ground energy state, also produce later internal conversion
Internal conversion is a non-radioactive, atomic decay process where an excited nucleus interacts electromagnetically with one of the orbital electrons of an atom. This causes the electron to be emitted (ejected) from the atom. Thus, in internal ...
and gamma decay in almost 0.5% of the time.
More common in heavy nuclides is competition between alpha and beta decay. The daughter nuclides will then normally decay through beta or alpha, respectively, to end up in the same place.
Radioactive decay results in a reduction of summed rest mass
Mass is an intrinsic property of a body. It was traditionally believed to be related to the quantity of matter in a physical body, until the discovery of the atom and particle physics. It was found that different atoms and different eleme ...
, once the released energy (the ''disintegration energy'') has escaped in some way. Although decay energy
The decay energy is the energy change of a nucleus having undergone a radioactive decay. Radioactive decay is the process in which an unstable atomic nucleus loses energy by emitting ionizing particles and radiation. This decay, or loss of energy ...
is sometimes defined as associated with the difference between the mass of the parent nuclide products and the mass of the decay products, this is true only of rest mass measurements, where some energy has been removed from the product system. This is true because the decay energy must always carry mass with it, wherever it appears (see mass in special relativity) according to the formula ''E'' = ''mc''2. The decay energy is initially released as the energy of emitted photons plus the kinetic energy of massive emitted particles (that is, particles that have rest mass). If these particles come to thermal equilibrium with their surroundings and photons are absorbed, then the decay energy is transformed to thermal energy, which retains its mass.
Decay energy, therefore, remains associated with a certain measure of the mass of the decay system, called invariant mass, which does not change during the decay, even though the energy of decay is distributed among decay particles. The energy of photons, the kinetic energy of emitted particles, and, later, the thermal energy of the surrounding matter, all contribute to the invariant mass of the system. Thus, while the sum of the rest masses of the particles is not conserved in radioactive decay, the ''system'' mass and system invariant mass (and also the system total energy) is conserved throughout any decay process. This is a restatement of the equivalent laws of conservation of energy and conservation of mass
In physics and chemistry, the law of conservation of mass or principle of mass conservation states that for any system closed to all transfers of matter and energy, the mass of the system must remain constant over time, as the system's mass can ...
.
List of decay modes
Rates
The ''decay rate'', or ''activity'', of a radioactive substance is characterized by the following time-independent parameters: * The '' half-life'', , is the time taken for the activity of a given amount of a radioactive substance to decay to half of its initial value. * The '' decay constant'', "lambda
Lambda (}, ''lám(b)da'') is the 11th letter of the Greek alphabet, representing the voiced alveolar lateral approximant . In the system of Greek numerals, lambda has a value of 30. Lambda is derived from the Phoenician Lamed . Lambda gave ri ...
", the reciprocal of the mean lifetime (in ), sometimes referred to as simply ''decay rate''.
* The '' mean lifetime'', "tau
Tau (uppercase Τ, lowercase τ, or \boldsymbol\tau; el, ταυ ) is the 19th letter of the Greek alphabet, representing the voiceless dental or alveolar plosive . In the system of Greek numerals, it has a value of 300.
The name in English ...
", the average lifetime (1/ e life) of a radioactive particle before decay.
Although these are constants, they are associated with the statistical behavior of populations of atoms. In consequence, predictions using these constants are less accurate for minuscule samples of atoms.
In principle a half-life, a third-life, or even a (1/√2)-life, can be used in exactly the same way as half-life; but the mean life and half-life have been adopted as standard times associated with exponential decay.
Those parameters can be related to the following time-dependent parameters:
* ''Total activity'', , is the number of decays per unit time of a radioactive sample.
* ''Number of particles'', , is the total number of particles
The particle number (or number of particles) of a thermodynamic system, conventionally indicated with the letter ''N'', is the number of constituent particles in that system. The particle number is a fundamental parameter in thermodynamics which is ...
in the sample.
* ''Specific activity'', , is the number of decays per unit time per amount of substance of the sample at time set to zero (). "Amount of substance" can be the mass, volume or moles of the initial sample.
These are related as follows:
:
where ''N''0 is the initial amount of active substance — substance that has the same percentage of unstable particles as when the substance was formed.
Mathematics
Universal law
The mathematics of radioactive decay depend on a key assumption that a nucleus of a radionuclide has no "memory" or way of translating its history into its present behavior. A nucleus does not "age" with the passage of time. Thus, the probability of its breaking down does not increase with time but stays constant, no matter how long the nucleus has existed. This constant probability may differ greatly between one type of nucleus and another, leading to the many different observed decay rates. However, whatever the probability is, it does not change over time. This is in marked contrast to complex objects that do show aging, such as automobiles and humans. These aging systems do have a chance of breakdown per unit of time that increases from the moment they begin their existence. Aggregate processes, like the radioactive decay of a lump of atoms, for which the single-event probability of realization is very small but in which the number of time-slices is so large that there is nevertheless a reasonable rate of events, are modelled by thePoisson distribution
In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time or space if these events occur with a known co ...
, which is discrete. Radioactive decay and nuclear particle reactions are two examples of such aggregate processes. The mathematics of Poisson processes reduce to the law of exponential decay, which describes the statistical behaviour of a large number of nuclei, rather than one individual nucleus. In the following formalism, the number of nuclei or the nuclei population ''N'', is of course a discrete variable (a natural number
In mathematics, the natural numbers are those numbers used for counting (as in "there are ''six'' coins on the table") and ordering (as in "this is the ''third'' largest city in the country").
Numbers used for counting are called ''cardinal ...
)—but for any physical sample ''N'' is so large that it can be treated as a continuous variable. Differential calculus is used to model the behaviour of nuclear decay.
One-decay process
Consider the case of a nuclide that decays into another by some process (emission of other particles, likeelectron neutrino
The electron neutrino () is an elementary particle which has zero electric charge and a spin of . Together with the electron, it forms the first generation of leptons, hence the name electron neutrino. It was first hypothesized by Wolfgang Pauli ...
s and electron
The electron ( or ) is a subatomic particle with a negative one elementary electric charge. Electrons belong to the first generation of the lepton particle family,
and are generally thought to be elementary particles because they have no ...
s e− as in beta decay
In nuclear physics, beta decay (β-decay) is a type of radioactive decay in which a beta particle (fast energetic electron or positron) is emitted from an atomic nucleus, transforming the original nuclide to an isobar of that nuclide. For ...
, are irrelevant in what follows). The decay of an unstable nucleus is entirely random in time so it is impossible to predict when a particular atom will decay. However, it is equally likely to decay at any instant in time. Therefore, given a sample of a particular radioisotope, the number of decay events expected to occur in a small interval of time is proportional to the number of atoms present , that is
:
Particular radionuclides decay at different rates, so each has its own decay constant . The expected decay is proportional to an increment of time, :
The negative sign indicates that decreases as time increases, as the decay events follow one after another. The solution to this first-order differential equation
In mathematics, a differential equation is an equation that relates one or more unknown functions and their derivatives. In applications, the functions generally represent physical quantities, the derivatives represent their rates of change, an ...
is the function
Function or functionality may refer to:
Computing
* Function key, a type of key on computer keyboards
* Function model, a structured representation of processes in a system
* Function object or functor or functionoid, a concept of object-oriente ...
:
:
where is the value of at time = 0, with the decay constant expressed as
We have for all time :
:
where is the constant number of particles throughout the decay process, which is equal to the initial number of nuclides since this is the initial substance.
If the number of non-decayed nuclei is:
:
then the number of nuclei of (i.e. the number of decayed nuclei) is
:
The number of decays observed over a given interval obeys Poisson statistics. If the average number of decays is , the probability of a given number of decays is
:
Chain-decay processes
=Chain of two decays
= Now consider the case of a chain of two decays: one nuclide decaying into another by one process, then decaying into another by a second process, i.e. '. The previous equation cannot be applied to the decay chain, but can be generalized as follows. Since decays into , ''then'' decays into , the activity of adds to the total number of nuclides in the present sample, ''before'' those nuclides decay and reduce the number of nuclides leading to the later sample. In other words, the number of second generation nuclei increases as a result of the first generation nuclei decay of , and decreases as a result of its own decay into the third generation nuclei .Introductory Nuclear Physics, K.S. Krane, 1988, John Wiley & Sons Inc, The sum of these two terms gives the law for a decay chain for two nuclides: : The rate of change of , that is , is related to the changes in the amounts of and , can increase as is produced from and decrease as produces . Re-writing using the previous results: The subscripts simply refer to the respective nuclides, i.e. is the number of nuclides of type ; is the initial number of nuclides of type ; is the decay constant for – and similarly for nuclide . Solving this equation for gives: : In the case where is a stable nuclide ( = 0), this equation reduces to the previous solution: : as shown above for one decay. The solution can be found by the integration factor method, where the integrating factor is . This case is perhaps the most useful since it can derive both the one-decay equation (above) and the equation for multi-decay chains (below) more directly.=Chain of any number of decays
= For the general case of any number of consecutive decays in a decay chain, i.e. , where is the number of decays and is a dummy index (), each nuclide population can be found in terms of the previous population. In this case , , ..., . Using the above result in a recursive form: : The general solution to the recursive problem is given by Bateman's equations:Alternative modes
In all of the above examples, the initial nuclide decays into just one product. Consider the case of one initial nuclide that can decay into either of two products, that is ' and ' in parallel. For example, in a sample ofpotassium-40
Potassium-40 (40K) is a radioactive isotope of potassium which has a long half-life of 1.25 billion years. It makes up about 0.012% (120 ppm) of the total amount of potassium found in nature.
Potassium-40 undergoes three types of radioactive d ...
, 89.3% of the nuclei decay to calcium-40 and 10.7% to argon-40. We have for all time :
:
which is constant, since the total number of nuclides remains constant. Differentiating with respect to time:
:
defining the ''total decay constant'' in terms of the sum of ''partial decay constants'' and :
:
Solving this equation for :
:
where is the initial number of nuclide A. When measuring the production of one nuclide, one can only observe the total decay constant . The decay constants and determine the probability for the decay to result in products or as follows:
:
:
because the fraction of nuclei decay into while the fraction of nuclei decay into .
Corollaries of laws
The above equations can also be written using quantities related to the number of nuclide particles in a sample; * The activity: . * The amount of substance: . * Themass
Mass is an intrinsic property of a body. It was traditionally believed to be related to the quantity of matter in a physical body, until the discovery of the atom and particle physics. It was found that different atoms and different eleme ...
: .
where = is the Avogadro constant, is the molar mass
In chemistry, the molar mass of a chemical compound is defined as the mass of a sample of that compound divided by the amount of substance which is the number of moles in that sample, measured in moles. The molar mass is a bulk, not molecular, ...
of the substance in kg/mol, and the amount of the substance is in moles Moles can refer to:
* Moles de Xert, a mountain range in the Baix Maestrat comarca, Valencian Community, Spain
* The Moles (Australian band)
*The Moles, alter ego of Scottish band Simon Dupree and the Big Sound
People
*Abraham Moles, French engin ...
.
Decay timing: definitions and relations
Time constant and mean-life
For the one-decay solution ': : the equation indicates that the decay constant has units of , and can thus also be represented as 1/, where is a characteristic time of the process called the ''time constant In physics and engineering, the time constant, usually denoted by the Greek letter (tau), is the parameter characterizing the response to a step input of a first-order, linear time-invariant (LTI) system.Concretely, a first-order LTI system is a s ...
''.
In a radioactive decay process, this time constant is also the mean lifetime for decaying atoms. Each atom "lives" for a finite amount of time before it decays, and it may be shown that this mean lifetime is the arithmetic mean of all the atoms' lifetimes, and that it is , which again is related to the decay constant as follows:
:
This form is also true for two-decay processes simultaneously ', inserting the equivalent values of decay constants (as given above)
:
into the decay solution leads to:
:

Half-life
A more commonly used parameter is the half-life . Given a sample of a particular radionuclide, the half-life is the time taken for half the radionuclide's atoms to decay. For the case of one-decay nuclear reactions: : the half-life is related to the decay constant as follows: set and = to obtain : This relationship between the half-life and the decay constant shows that highly radioactive substances are quickly spent, while those that radiate weakly endure longer. Half-lives of known radionuclides vary by almost 54 orders of magnitude, from more than years ( sec) for the very nearly stable nuclide 128Te, to seconds for the highly unstable nuclide 5H. The factor of in the above relations results from the fact that the concept of "half-life" is merely a way of selecting a different base other than the natural base for the lifetime expression. The time constant is the -life, the time until only 1/''e'' remains, about 36.8%, rather than the 50% in the half-life of a radionuclide. Thus, is longer than . The following equation can be shown to be valid: : Since radioactive decay is exponential with a constant probability, each process could as easily be described with a different constant time period that (for example) gave its "(1/3)-life" (how long until only 1/3 is left) or "(1/10)-life" (a time period until only 10% is left), and so on. Thus, the choice of and for marker-times, are only for convenience, and from convention. They reflect a fundamental principle only in so much as they show that the ''same proportion'' of a given radioactive substance will decay, during any time-period that one chooses. Mathematically, the life for the above situation would be found in the same way as aboveby setting ', and substituting into the decay solution to obtain :Example for carbon-14
Carbon-14 has a half-life of years and a decay rate of 14 disintegrations per minute (dpm) per gram of natural carbon. If an artifact is found to have radioactivity of 4 dpm per gram of its present C, we can find the approximate age of the object using the above equation: : where: :Changing rates
The radioactive decay modes of electron capture andinternal conversion
Internal conversion is a non-radioactive, atomic decay process where an excited nucleus interacts electromagnetically with one of the orbital electrons of an atom. This causes the electron to be emitted (ejected) from the atom. Thus, in internal ...
are known to be slightly sensitive to chemical and environmental effects that change the electronic structure of the atom, which in turn affects the presence of 1s and 2s electrons that participate in the decay process. A small number of nuclides are affected. For example, chemical bonds
A chemical bond is a lasting attraction between atoms or ions that enables the formation of molecules and crystals. The bond may result from the electrostatic force between oppositely charged ions as in ionic bonds, or through the sharing of ...
can affect the rate of electron capture to a small degree (in general, less than 1%) depending on the proximity of electrons to the nucleus. In 7Be, a difference of 0.9% has been observed between half-lives in metallic and insulating environments. This relatively large effect is because beryllium is a small atom whose valence electrons are in 2s atomic orbital
In atomic theory and quantum mechanics, an atomic orbital is a function describing the location and wave-like behavior of an electron in an atom. This function can be used to calculate the probability of finding any electron of an atom in an ...
s, which are subject to electron capture in 7Be because (like all s atomic orbitals in all atoms) they naturally penetrate into the nucleus.
In 1992, Jung et al. of the Darmstadt Heavy-Ion Research group observed an accelerated β− decay of 163Dy66+. Although neutral 163Dy is a stable isotope, the fully ionized 163Dy66+ undergoes β− decay into the K and L shells to 163Ho66+ with a half-life of 47 days.
Rhenium-187 is another spectacular example. 187Re normally undergoes beta decay
In nuclear physics, beta decay (β-decay) is a type of radioactive decay in which a beta particle (fast energetic electron or positron) is emitted from an atomic nucleus, transforming the original nuclide to an isobar of that nuclide. For ...
to 187Os with a half-life of 41.6 × 109 years, but studies using fully ionised 187 Re atoms (bare nuclei) have found that this can decrease to only 32.9 years. This is attributed to " bound-state β− decay" of the fully ionised atom – the electron is emitted into the "K-shell" (1s atomic orbital), which cannot occur for neutral atoms in which all low-lying bound states are occupied.
 A number of experiments have found that decay rates of other modes of artificial and naturally occurring radioisotopes are, to a high degree of precision, unaffected by external conditions such as temperature, pressure, the chemical environment, and electric, magnetic, or gravitational fields. Comparison of laboratory experiments over the last century, studies of the Oklo natural nuclear reactor (which exemplified the effects of thermal neutrons on nuclear decay), and astrophysical observations of the luminosity decays of distant supernovae (which occurred far away so the light has taken a great deal of time to reach us), for example, strongly indicate that unperturbed decay rates have been constant (at least to within the limitations of small experimental errors) as a function of time as well.
Recent results suggest the possibility that decay rates might have a weak dependence on environmental factors. It has been suggested that measurements of decay rates of silicon-32, manganese-54, and radium-226 exhibit small seasonal variations (of the order of 0.1%). However, such measurements are highly susceptible to systematic errors, and a subsequent paper has found no evidence for such correlations in seven other isotopes (22Na, 44Ti, 108Ag, 121Sn, 133Ba, 241Am, 238Pu), and sets upper limits on the size of any such effects. The decay of
A number of experiments have found that decay rates of other modes of artificial and naturally occurring radioisotopes are, to a high degree of precision, unaffected by external conditions such as temperature, pressure, the chemical environment, and electric, magnetic, or gravitational fields. Comparison of laboratory experiments over the last century, studies of the Oklo natural nuclear reactor (which exemplified the effects of thermal neutrons on nuclear decay), and astrophysical observations of the luminosity decays of distant supernovae (which occurred far away so the light has taken a great deal of time to reach us), for example, strongly indicate that unperturbed decay rates have been constant (at least to within the limitations of small experimental errors) as a function of time as well.
Recent results suggest the possibility that decay rates might have a weak dependence on environmental factors. It has been suggested that measurements of decay rates of silicon-32, manganese-54, and radium-226 exhibit small seasonal variations (of the order of 0.1%). However, such measurements are highly susceptible to systematic errors, and a subsequent paper has found no evidence for such correlations in seven other isotopes (22Na, 44Ti, 108Ag, 121Sn, 133Ba, 241Am, 238Pu), and sets upper limits on the size of any such effects. The decay of radon-222
Radon-222 (222Rn, Rn-222, historically radium emanation or radon) is the most stable isotope of radon, with a half-life of approximately 3.8 days. It is transient in the decay chain of primordial uranium-238 and is the immediate decay product of ...
was once reported to exhibit large 4% peak-to-peak seasonal variations (see plot), which were proposed to be related to either solar flare
A solar flare is an intense localized eruption of electromagnetic radiation in the Sun's atmosphere. Flares occur in active regions and are often, but not always, accompanied by coronal mass ejections, solar particle events, and other sol ...
activity or the distance from the Sun, but detailed analysis of the experiment's design flaws, along with comparisons to other, much more stringent and systematically controlled, experiments refute this claim.
GSI anomaly
An unexpected series of experimental results for the rate of decay of heavy highly charged radioactive ions circulating in astorage ring
A storage ring is a type of circular particle accelerator in which a continuous or pulsed particle beam may be kept circulating typically for many hours. Storage of a particular particle depends upon the mass, momentum and usually the charge of t ...
has provoked theoretical activity in an effort to find a convincing explanation. The rates of weak decay of two radioactive species with half lives of about 40 s and 200 s are found to have a significant oscillatory modulation, with a period of about 7 s.
The observed phenomenon is known as the GSI anomaly, as the storage ring is a facility at the GSI Helmholtz Centre for Heavy Ion Research
The GSI Helmholtz Centre for Heavy Ion Research (german: GSI Helmholtzzentrum für Schwerionenforschung) is a federally and state co-funded heavy ion () research center in the Wixhausen suburb of Darmstadt, Germany. It was founded in 1969 as th ...
in Darmstadt, Germany
Germany,, officially the Federal Republic of Germany, is a country in Central Europe. It is the second most populous country in Europe after Russia, and the most populous member state of the European Union. Germany is situated betwe ...
. As the decay process produces an electron neutrino
The electron neutrino () is an elementary particle which has zero electric charge and a spin of . Together with the electron, it forms the first generation of leptons, hence the name electron neutrino. It was first hypothesized by Wolfgang Pauli ...
, some of the proposed explanations for the observed rate oscillation invoke neutrino properties. Initial ideas related to flavour oscillation met with skepticism. A more recent proposal involves mass differences between neutrino mass eigenstates.
Theoretical basis
Theneutron
The neutron is a subatomic particle, symbol or , which has a neutral (not positive or negative) charge, and a mass slightly greater than that of a proton. Protons and neutrons constitute the nuclei of atoms. Since protons and neutrons beh ...
s and protons that constitute nuclei, as well as other particles that approach close enough to them, are governed by several interactions. The nuclear force
The nuclear force (or nucleon–nucleon interaction, residual strong force, or, historically, strong nuclear force) is a force that acts between the protons and neutrons of atoms. Neutrons and protons, both nucleons, are affected by the nucle ...
(also known as ''residual'' strong force
The strong interaction or strong force is a fundamental interaction that confines quarks into proton, neutron, and other hadron particles. The strong interaction also binds neutrons and protons to create atomic nuclei, where it is called the ...
), not observed at the familiar macroscopic
The macroscopic scale is the length scale on which objects or phenomena are large enough to be visible with the naked eye, without magnifying optical instruments. It is the opposite of microscopic.
Overview
When applied to physical phenomena a ...
scale, is the most powerful force over subatomic distances. The electrostatic force
Coulomb's inverse-square law, or simply Coulomb's law, is an experimental law of physics that quantifies the amount of force between two stationary, electrically charged particles. The electric force between charged bodies at rest is convention ...
is almost always significant, and, in the case of beta decay
In nuclear physics, beta decay (β-decay) is a type of radioactive decay in which a beta particle (fast energetic electron or positron) is emitted from an atomic nucleus, transforming the original nuclide to an isobar of that nuclide. For ...
, the weak nuclear force is also involved.
The combined effects of these forces produces a number of different phenomena in which energy may be released by rearrangement of particles in the nucleus, or else the change of one type of particle into others. These rearrangements and transformations may be hindered energetically so that they do not occur immediately. In certain cases, random quantum vacuum fluctuations
In quantum physics, a quantum fluctuation (also known as a vacuum state fluctuation or vacuum fluctuation) is the temporary random change in the amount of energy in a point in space, as prescribed by Werner Heisenberg's uncertainty principle. ...
are theorized to promote relaxation to a lower energy state (the "decay") in a phenomenon known as quantum tunneling
In physics, a quantum (plural quanta) is the minimum amount of any physical entity (physical property) involved in an interaction. The fundamental notion that a physical property can be "quantized" is referred to as "the hypothesis of quantizati ...
. Radioactive decay half-life of nuclides has been measured over timescales of 54 orders of magnitude, from seconds (for hydrogen-5) to seconds (for tellurium-128). The limits of these timescales are set by the sensitivity of instrumentation only, and there are no known natural limits to how brief or long a decay half-life for radioactive decay of a radionuclide may be.
The decay process, like all hindered energy transformations, may be analogized by a snowfield on a mountain. While friction
Friction is the force resisting the relative motion of solid surfaces, fluid layers, and material elements sliding against each other. There are several types of friction:
*Dry friction is a force that opposes the relative lateral motion of ...
between the ice crystals may be supporting the snow's weight, the system is inherently unstable with regard to a state of lower potential energy. A disturbance would thus facilitate the path to a state of greater entropy; the system will move towards the ground state, producing heat, and the total energy will be distributable over a larger number of quantum states thus resulting in an avalanche
An avalanche is a rapid flow of snow down a slope, such as a hill or mountain.
Avalanches can be set off spontaneously, by such factors as increased precipitation or snowpack weakening, or by external means such as humans, animals, and eart ...
. The ''total'' energy does not change in this process, but, because of the second law of thermodynamics, avalanches have only been observed in one direction and that is toward the " ground state" — the state with the largest number of ways in which the available energy could be distributed.
Such a collapse (a gamma-ray ''decay event'') requires a specific activation energy. For a snow avalanche, this energy comes as a disturbance from outside the system, although such disturbances can be arbitrarily small. In the case of an excited atomic nucleus
The atomic nucleus is the small, dense region consisting of protons and neutrons at the center of an atom, discovered in 1911 by Ernest Rutherford based on the 1909 Geiger–Marsden gold foil experiment. After the discovery of the neutron ...
decaying by gamma radiation in a spontaneous emission of electromagnetic radiation, the arbitrarily small disturbance comes from quantum vacuum fluctuations
In quantum physics, a quantum fluctuation (also known as a vacuum state fluctuation or vacuum fluctuation) is the temporary random change in the amount of energy in a point in space, as prescribed by Werner Heisenberg's uncertainty principle. ...
.
A radioactive nucleus (or any excited system in quantum mechanics) is unstable, and can, thus, ''spontaneously'' stabilize to a less-excited system. The resulting transformation alters the structure of the nucleus and results in the emission of either a photon or a high-velocity particle that has mass (such as an electron, alpha particle
Alpha particles, also called alpha rays or alpha radiation, consist of two protons and two neutrons bound together into a particle identical to a helium-4 nucleus. They are generally produced in the process of alpha decay, but may also be pr ...
, or other type).
Occurrence and applications
According to the Big Bang theory, stable isotopes of the lightest three elements ( H, He, and traces of Li) were produced very shortly after the emergence of the universe, in a process calledBig Bang nucleosynthesis
In physical cosmology, Big Bang nucleosynthesis (abbreviated BBN, also known as primordial nucleosynthesis) is the production of nuclei other than those of the lightest isotope of hydrogen ( hydrogen-1, 1H, having a single proton as a nucleu ...
. These lightest stable nuclides (including deuterium) survive to today, but any radioactive isotopes of the light elements produced in the Big Bang (such as tritium
Tritium ( or , ) or hydrogen-3 (symbol T or H) is a rare and radioactive isotope of hydrogen with half-life about 12 years. The nucleus of tritium (t, sometimes called a ''triton'') contains one proton and two neutrons, whereas the nucleus of ...
) have long since decayed. Isotopes of elements heavier than boron were not produced at all in the Big Bang, and these first five elements do not have any long-lived radioisotopes. Thus, all radioactive nuclei are, therefore, relatively young with respect to the birth of the universe, having formed later in various other types of nucleosynthesis
Nucleosynthesis is the process that creates new atomic nuclei from pre-existing nucleons (protons and neutrons) and nuclei. According to current theories, the first nuclei were formed a few minutes after the Big Bang, through nuclear reactions in ...
in stars (in particular, supernovae), and also during ongoing interactions between stable isotopes and energetic particles. For example, carbon-14, a radioactive nuclide with a half-life of only years, is constantly produced in Earth's upper atmosphere due to interactions between cosmic rays and nitrogen.
Nuclides that are produced by radioactive decay are called radiogenic nuclide
A radiogenic nuclide is a nuclide that is produced by a process of radioactive decay. It may itself be radioactive (a radionuclide) or stable (a stable nuclide).
Radiogenic nuclides (more commonly referred to as radiogenic isotopes) form some of ...
s, whether they themselves are stable or not. There exist stable radiogenic nuclides that were formed from short-lived extinct radionuclide
An extinct radionuclide is a radionuclide that was formed by nucleosynthesis before the formation of the Solar System, about 4.6 billion years ago, but has since decayed to virtually zero abundance and is no longer detectable as a primordial nuc ...
s in the early Solar System. The extra presence of these stable radiogenic nuclides (such as xenon-129 from extinct iodine-129
Iodine-129 (129I) is a long-lived radioisotope of iodine which occurs naturally, but also is of special interest in the monitoring and effects of man-made nuclear fission products, where it serves as both tracer and potential radiological contamin ...
) against the background of primordial stable nuclide
Stable nuclides are nuclides that are not radioactive and so (unlike radionuclides) do not spontaneously undergo radioactive decay. When such nuclides are referred to in relation to specific elements, they are usually termed stable isotopes.
Th ...
s can be inferred by various means.
Radioactive decay has been put to use in the technique of radioisotopic labeling, which is used to track the passage of a chemical substance through a complex system (such as a living organism
In biology, an organism () is any living system that functions as an individual entity. All organisms are composed of cells (cell theory). Organisms are classified by taxonomy into groups such as multicellular animals, plants, and ...
). A sample of the substance is synthesized with a high concentration of unstable atoms. The presence of the substance in one or another part of the system is determined by detecting the locations of decay events.
On the premise that radioactive decay is truly random (rather than merely chaotic), it has been used in hardware random-number generators. Because the process is not thought to vary significantly in mechanism over time, it is also a valuable tool in estimating the absolute ages of certain materials. For geological materials, the radioisotopes and some of their decay products become trapped when a rock solidifies, and can then later be used (subject to many well-known qualifications) to estimate the date of the solidification. These include checking the results of several simultaneous processes and their products against each other, within the same sample. In a similar fashion, and also subject to qualification, the rate of formation of carbon-14 in various eras, the date of formation of organic matter within a certain period related to the isotope's half-life may be estimated, because the carbon-14 becomes trapped when the organic matter grows and incorporates the new carbon-14 from the air. Thereafter, the amount of carbon-14 in organic matter decreases according to decay processes that may also be independently cross-checked by other means (such as checking the carbon-14 in individual tree rings, for example).
Szilard–Chalmers effect
The Szilard–Chalmers effect is the breaking of a chemical bond as a result of a kinetic energy imparted from radioactive decay. It operates by the absorption of neutrons by an atom and subsequent emission of gamma rays, often with significant amounts of kinetic energy. This kinetic energy, byNewton's third law
Newton's laws of motion are three basic laws of classical mechanics that describe the relationship between the motion of an object and the forces acting on it. These laws can be paraphrased as follows:
# A body remains at rest, or in moti ...
, pushes back on the decaying atom, which causes it to move with enough speed to break a chemical bond. This effect can be used to separate isotopes by chemical means.
The Szilard–Chalmers effect was discovered in 1934 by Leó Szilárd
Leo Szilard (; hu, Szilárd Leó, pronounced ; born Leó Spitz; February 11, 1898 – May 30, 1964) was a Hungarian-German-American physicist and inventor. He conceived the nuclear chain reaction in 1933, patented the idea of a nuclear ...
and Thomas A. Chalmers. They observed that after bombardment by neutrons, the breaking of a bond in liquid ethyl iodide allowed radioactive iodine to be removed.
Origins of radioactive nuclides
Radioactive primordial nuclides found in theEarth
Earth is the third planet from the Sun and the only astronomical object known to harbor life. While large volumes of water can be found throughout the Solar System, only Earth sustains liquid surface water. About 71% of Earth's surfa ...
are residues from ancient supernova explosions that occurred before the formation of the Solar System
The Solar System Capitalization of the name varies. The International Astronomical Union, the authoritative body regarding astronomical nomenclature, specifies capitalizing the names of all individual astronomical objects but uses mixed "Solar ...
. They are the fraction of radionuclides that survived from that time, through the formation of the primordial solar nebula, through planet accretion, and up to the present time. The naturally occurring short-lived radiogenic radionuclides found in today's rocks, are the daughters of those radioactive primordial nuclides. Another minor source of naturally occurring radioactive nuclides are cosmogenic nuclide
Cosmogenic nuclides (or cosmogenic isotopes) are rare nuclides (isotopes) created when a high-energy cosmic ray interacts with the nucleus of an '' in situ'' Solar System atom, causing nucleons (protons and neutrons) to be expelled from the atom ...
s, that are formed by cosmic ray bombardment of material in the Earth's atmosphere or crust. The decay of the radionuclides in rocks of the Earth's mantle and crust contribute significantly to Earth's internal heat budget
Earth's internal heat budget is fundamental to the thermal history of the Earth. The flow of heat from Earth's interior to the surface is estimated at 47±2 terawatts (TW)Davies, J. H., & Davies, D. R. (2010). Earth's surface heat flux. Solid ...
.
Decay chains and multiple modes
The daughter nuclide of a decay event may also be unstable (radioactive). In this case, it too will decay, producing radiation. The resulting second daughter nuclide may also be radioactive. This can lead to a sequence of several decay events called a ''decay chain
In nuclear science, the decay chain refers to a series of radioactive decays of different radioactive decay products as a sequential series of transformations. It is also known as a "radioactive cascade". Most radioisotopes do not decay dire ...
'' (see this article for specific details of important natural decay chains). Eventually, a stable nuclide is produced. Any decay daughters that are the result of an alpha decay will also result in helium atoms being created.
 An example is the natural decay chain of 238U:
* Uranium-238 decays, through alpha-emission, with a half-life of billion years to thorium-234
* which decays, through beta-emission, with a half-life of days to protactinium-234m
* which decays, through beta-emission, with a half-life of minutes to
An example is the natural decay chain of 238U:
* Uranium-238 decays, through alpha-emission, with a half-life of billion years to thorium-234
* which decays, through beta-emission, with a half-life of days to protactinium-234m
* which decays, through beta-emission, with a half-life of minutes to uranium-234
Uranium-234 (234U or U-234) is an isotope of uranium. In natural uranium and in uranium ore, 234U occurs as an indirect decay product of uranium-238, but it makes up only 0.0055% (55 parts per million) of the raw uranium because its half-lif ...
* which decays, through alpha-emission, with a half-life of thousand years to thorium-230
Thorium (90Th) has seven naturally occurring isotopes but none are stable. One isotope, 232Th, is ''relatively'' stable, with a half-life of 1.405×1010 years, considerably longer than the age of the Earth, and even slightly longer than the gene ...
* which decays, through alpha-emission, with a half-life of thousand years to radium-226
* which decays, through alpha-emission, with a half-life of thousand years to radon-222
Radon-222 (222Rn, Rn-222, historically radium emanation or radon) is the most stable isotope of radon, with a half-life of approximately 3.8 days. It is transient in the decay chain of primordial uranium-238 and is the immediate decay product of ...
* which decays, through alpha-emission, with a half-life of days to polonium-218
* which decays, through alpha-emission, with a half-life of minutes to lead-214
* which decays, through beta-emission, with a half-life of minutes to bismuth-214
* which decays, through beta-emission, with a half-life of minutes to polonium-214
* which decays, through alpha-emission, with a half-life of microseconds to lead-210
Lead (82Pb) has four stable isotopes: 204Pb, 206Pb, 207Pb, 208Pb. Lead-204 is entirely a primordial nuclide and is not a radiogenic nuclide. The three isotopes lead-206, lead-207, and lead-208 represent the ends of three decay chains: the uranium ...
* which decays, through beta-emission, with a half-life of years to bismuth-210
* which decays, through beta-emission, with a half-life of days to polonium-210
* which decays, through alpha-emission, with a half-life of days to lead-206
Lead (82Pb) has four stable isotopes: 204Pb, 206Pb, 207Pb, 208Pb. Lead-204 is entirely a primordial nuclide and is not a radiogenic nuclide. The three isotopes lead-206, lead-207, and lead-208 represent the ends of three decay chains: the urani ...
, which is a stable nuclide.
Some radionuclides may have several different paths of decay. For example, % of bismuth-212 decays, through alpha-emission, to thallium-208 while % of bismuth-212 decays, through beta-emission, to polonium-212. Both thallium-208 and polonium-212 are radioactive daughter products of bismuth-212, and both decay directly to stable lead-208.
Hazard warning signs
/ref> File:Dangclass7.svg, The dangerous goods transport classification sign for radioactive materials
See also
* Actinides in the environment * Background radiation * Chernobyl disaster *Crimes involving radioactive substances
This is a list of criminal (or arguably, allegedly, or potentially criminal) acts intentionally involving radioactive substances. Inclusion in this list does not necessarily imply that anyone involved was guilty of a crime. For accidents or crimes ...
* Decay correction
* Fallout shelter
A fallout shelter is an enclosed space specially designated to protect occupants from radioactive debris or fallout resulting from a nuclear explosion. Many such shelters were constructed as civil defense measures during the Cold War.
During ...
* Geiger counter
* Induced radioactivity
Induced radioactivity, also called artificial radioactivity or man-made radioactivity, is the process of using radiation to make a previously stable material radioactive. The husband and wife team of Irène Joliot-Curie and Frédéric Joliot-Curi ...
* Lists of nuclear disasters and radioactive incidents
These are lists of nuclear disasters and radioactive incidents.
Main lists
* List of attacks on nuclear plants
* List of Chernobyl-related articles
* List of civilian nuclear accidents
* List of civilian radiation accidents
* List of ...
* National Council on Radiation Protection and Measurements The National Council on Radiation Protection and Measurements (NCRP), formerly the National Committee on Radiation Protection and Measurements, and before that the Advisory Committee on X-Ray and Radium Protection (ACXRP), is a U.S. organization. ...
* Nuclear engineering
* Nuclear pharmacy
* Nuclear physics
Nuclear physics is the field of physics that studies atomic nuclei and their constituents and interactions, in addition to the study of other forms of nuclear matter.
Nuclear physics should not be confused with atomic physics, which studies the ...
* Nuclear power
Nuclear power is the use of nuclear reactions to produce electricity. Nuclear power can be obtained from nuclear fission, nuclear decay and nuclear fusion reactions. Presently, the vast majority of electricity from nuclear power is produced ...
* Particle decay
In particle physics, particle decay is the spontaneous process of one unstable subatomic particle transforming into multiple other particles. The particles created in this process (the ''final state'') must each be less massive than the original, ...
* Poisson process
In probability, statistics and related fields, a Poisson point process is a type of random mathematical object that consists of points randomly located on a mathematical space with the essential feature that the points occur independently of one ...
* Radiation therapy
Radiation therapy or radiotherapy, often abbreviated RT, RTx, or XRT, is a therapy using ionizing radiation, generally provided as part of cancer treatment to control or kill malignant cells and normally delivered by a linear accelerator. Radi ...
* Radioactive contamination
Radioactive contamination, also called radiological pollution, is the deposition of, or presence of radioactive substances on surfaces or within solids, liquids, or gases (including the human body), where their presence is unintended or undesirab ...
* Radioactivity in biology
* Radiometric dating
Radiometric dating, radioactive dating or radioisotope dating is a technique which is used to date materials such as rocks or carbon, in which trace radioactive impurities were selectively incorporated when they were formed. The method compares ...
* Transient equilibrium
Notes
References
Inline
General
"Radioactivity"
Encyclopædia Britannica. 2006.
Encyclopædia Britannica Online
An encyclopedia (American English) or encyclopædia (British English) is a reference work or compendium providing summaries of knowledge either general or special to a particular field or discipline. Encyclopedias are divided into article ...
. December 18, 2006
* Radio-activity by Ernest Rutherford Phd, Encyclopædia Britannica Eleventh Edition
External links
The Lund/LBNL Nuclear Data Search
– Contains tabulated information on radioactive decay types and energies.
Nomenclature of nuclear chemistry
The Live Chart of Nuclides – IAEA
Interactive Chart of Nuclides
Health Physics Society Public Education Website
*
Annotated bibliography for radioactivity from the Alsos Digital Library for Nuclear Issues
by Wolfgang Bauer
by David M. Harrison * "Henri Becquerel: The Discovery of Radioactivity", Becquerel's 1896 articles online and analyzed on
BibNum
' lick 'à télécharger' for English version/small>. * "Radioactive change", Rutherford & Soddy article (1903), online and analyzed on
Bibnum
' lick 'à télécharger' for English version/small>. {{DEFAULTSORT:Radioactive Decay Exponentials Poisson point processes