Logical implication on:
[Wikipedia]
[Google]
[Amazon]
 Logic is the study of correct
Logic is the study of correct
 Formal logic uses formal languages to express and analyze arguments. They normally have a very limited vocabulary and exact syntactic rules. These rules specify how their symbols can be combined to construct sentences, so-called
Formal logic uses formal languages to express and analyze arguments. They normally have a very limited vocabulary and exact syntactic rules. These rules specify how their symbols can be combined to construct sentences, so-called
 Arguments and inferences are either correct or incorrect. If they are correct then their premises support their conclusion. In the incorrect case, this support is missing. It can take different forms corresponding to the different types of reasoning. The strongest form of support corresponds to
Arguments and inferences are either correct or incorrect. If they are correct then their premises support their conclusion. In the incorrect case, this support is missing. It can take different forms corresponding to the different types of reasoning. The strongest form of support corresponds to
 First-order logic includes the same propositional connectives as propositional logic but differs from it because it articulates the internal structure of propositions. This happens through devices such as singular terms, which refer to particular objects, predicates, which refer to properties and relations, and quantifiers, which treat notions like "some" and "all". For example, to express the proposition "this raven is black", one may use the predicate for the property "black" and the singular term referring to the raven to form the expression . To express that some objects are black, the existential quantifier is combined with the variable to form the proposition . First-order logic contains various rules of inference that determine how expressions articulated this way can form valid arguments, for example, that one may infer from .
First-order logic includes the same propositional connectives as propositional logic but differs from it because it articulates the internal structure of propositions. This happens through devices such as singular terms, which refer to particular objects, predicates, which refer to properties and relations, and quantifiers, which treat notions like "some" and "all". For example, to express the proposition "this raven is black", one may use the predicate for the property "black" and the singular term referring to the raven to form the expression . To express that some objects are black, the existential quantifier is combined with the variable to form the proposition . First-order logic contains various rules of inference that determine how expressions articulated this way can form valid arguments, for example, that one may infer from .
 The term "mathematical logic" is sometimes used as a synonym of "formal logic". But in a more restricted sense, it refers to the study of logic within mathematics. Major subareas include
The term "mathematical logic" is sometimes used as a synonym of "formal logic". But in a more restricted sense, it refers to the study of logic within mathematics. Major subareas include
 Computational logic is the branch of logic and
Computational logic is the branch of logic and
 Logic is the study of correct
Logic is the study of correct reasoning
Reason is the capacity of consciously applying logic by drawing valid conclusions from new or existing information, with the aim of seeking the truth. It is associated with such characteristically human activities as philosophy, religion, scien ...
. It includes both formal and informal logic
Informal logic encompasses the principles of logic and logical thought outside of a formal setting (characterized by the usage of particular statements). However, the precise definition of "informal logic" is a matter of some dispute. Ralph H. ...
. Formal logic is the study of deductively valid inferences or logical truths. It examines how conclusions follow from premises based on the structure of arguments alone, independent of their topic and content. Informal logic is associated with informal fallacies, critical thinking
Critical thinking is the process of analyzing available facts, evidence, observations, and arguments to make sound conclusions or informed choices. It involves recognizing underlying assumptions, providing justifications for ideas and actions, ...
, and argumentation theory. Informal logic examines arguments expressed in natural language whereas formal logic uses formal language. When used as a countable noun, the term "a logic" refers to a specific logical formal system that articulates a proof system. Logic plays a central role in many fields, such as philosophy
Philosophy ('love of wisdom' in Ancient Greek) is a systematic study of general and fundamental questions concerning topics like existence, reason, knowledge, Value (ethics and social sciences), value, mind, and language. It is a rational an ...
, mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ...
, computer science
Computer science is the study of computation, information, and automation. Computer science spans Theoretical computer science, theoretical disciplines (such as algorithms, theory of computation, and information theory) to Applied science, ...
, and linguistics
Linguistics is the scientific study of language. The areas of linguistic analysis are syntax (rules governing the structure of sentences), semantics (meaning), Morphology (linguistics), morphology (structure of words), phonetics (speech sounds ...
.
Logic studies arguments, which consist of a set of premises that leads to a conclusion. An example is the argument from the premises "it's Sunday" and "if it's Sunday then I don't have to work" leading to the conclusion "I don't have to work." Premises and conclusions express proposition
A proposition is a statement that can be either true or false. It is a central concept in the philosophy of language, semantics, logic, and related fields. Propositions are the object s denoted by declarative sentences; for example, "The sky ...
s or claims that can be true or false. An important feature of propositions is their internal structure. For example, complex propositions are made up of simpler propositions linked by logical vocabulary like ( and) or ( if...then). Simple propositions also have parts, like "Sunday" or "work" in the example. The truth of a proposition usually depends on the meanings of all of its parts. However, this is not the case for logically true propositions. They are true only because of their logical structure independent of the specific meanings of the individual parts.
Arguments can be either correct or incorrect. An argument is correct if its premises support its conclusion. Deductive arguments have the strongest form of support: if their premises are true then their conclusion must also be true. This is not the case for ampliative Ampliative (from Latin ''ampliare'', "to enlarge"), a term used mainly in logic, meaning "extending" or "adding to that which is already known".
This terminology was often used by medieval logicians in the analyses of the temporal content of the ...
arguments, which arrive at genuinely new information not found in the premises. Many arguments in everyday discourse and the sciences are ampliative arguments. They are divided into inductive and abductive arguments. Inductive arguments are statistical generalizations, such as inferring that all ravens are black based on many individual observations of black ravens. Abductive arguments are inference
Inferences are steps in logical reasoning, moving from premises to logical consequences; etymologically, the word '' infer'' means to "carry forward". Inference is theoretically traditionally divided into deduction and induction, a distinct ...
s to the best explanation, for example, when a doctor concludes that a patient has a certain disease which explains the symptoms they suffer. Arguments that fall short of the standards of correct reasoning often embody fallacies
A fallacy is the use of invalid or otherwise faulty reasoning in the construction of an argument that may appear to be well-reasoned if unnoticed. The term was introduced in the Western intellectual tradition by the Aristotelian '' De Sophis ...
. Systems of logic are theoretical frameworks for assessing the correctness of arguments.
Logic has been studied since antiquity. Early approaches include Aristotelian logic
In logic and formal semantics, term logic, also known as traditional logic, syllogistic logic or Aristotelian logic, is a loose name for an approach to formal logic that began with Aristotle and was developed further in ancient history mostly b ...
, Stoic logic, Nyaya, and Mohism. Aristotelian logic focuses on reasoning in the form of syllogisms. It was considered the main system of logic in the Western world until it was replaced by modern formal logic, which has its roots in the work of late 19th-century mathematicians such as Gottlob Frege
Friedrich Ludwig Gottlob Frege (; ; 8 November 1848 – 26 July 1925) was a German philosopher, logician, and mathematician. He was a mathematics professor at the University of Jena, and is understood by many to be the father of analytic philos ...
. Today, the most commonly used system is classical logic
Classical logic (or standard logic) or Frege–Russell logic is the intensively studied and most widely used class of deductive logic. Classical logic has had much influence on analytic philosophy.
Characteristics
Each logical system in this c ...
. It consists of propositional logic and first-order logic. Propositional logic only considers logical relations between full propositions. First-order logic also takes the internal parts of propositions into account, like predicates and quantifiers. Extended logics accept the basic intuitions behind classical logic and apply it to other fields, such as metaphysics
Metaphysics is the branch of philosophy that examines the basic structure of reality. It is traditionally seen as the study of mind-independent features of the world, but some theorists view it as an inquiry into the conceptual framework of ...
, ethics
Ethics is the philosophy, philosophical study of Morality, moral phenomena. Also called moral philosophy, it investigates Normativity, normative questions about what people ought to do or which behavior is morally right. Its main branches inclu ...
, and epistemology
Epistemology is the branch of philosophy that examines the nature, origin, and limits of knowledge. Also called "the theory of knowledge", it explores different types of knowledge, such as propositional knowledge about facts, practical knowle ...
. Deviant logics, on the other hand, reject certain classical intuitions and provide alternative explanations of the basic laws of logic.
Definition
The word "logic" originates from the Greek word ''logos'', which has a variety of translations, such asreason
Reason is the capacity of consciously applying logic by drawing valid conclusions from new or existing information, with the aim of seeking the truth. It is associated with such characteristically human activities as philosophy, religion, scien ...
, discourse
Discourse is a generalization of the notion of a conversation to any form of communication. Discourse is a major topic in social theory, with work spanning fields such as sociology, anthropology, continental philosophy, and discourse analysis. F ...
, or language
Language is a structured system of communication that consists of grammar and vocabulary. It is the primary means by which humans convey meaning, both in spoken and signed language, signed forms, and may also be conveyed through writing syste ...
. Logic is traditionally defined as the study of the laws of thought or correct reasoning, and is usually understood in terms of inference
Inferences are steps in logical reasoning, moving from premises to logical consequences; etymologically, the word '' infer'' means to "carry forward". Inference is theoretically traditionally divided into deduction and induction, a distinct ...
s or argument
An argument is a series of sentences, statements, or propositions some of which are called premises and one is the conclusion. The purpose of an argument is to give reasons for one's conclusion via justification, explanation, and/or persu ...
s. Reasoning is the activity of drawing inferences. Arguments are the outward expression of inferences. An argument is a set of premises together with a conclusion. Logic is interested in whether arguments are correct, i.e. whether their premises support the conclusion. These general characterizations apply to logic in the widest sense, i.e., to both formal and informal logic
Informal logic encompasses the principles of logic and logical thought outside of a formal setting (characterized by the usage of particular statements). However, the precise definition of "informal logic" is a matter of some dispute. Ralph H. ...
since they are both concerned with assessing the correctness of arguments. Formal logic is the traditionally dominant field, and some logicians restrict logic to formal logic.
Formal logic
''Formal logic'' (also known as ''symbolic logic'') is widely used inmathematical logic
Mathematical logic is the study of Logic#Formal logic, formal logic within mathematics. Major subareas include model theory, proof theory, set theory, and recursion theory (also known as computability theory). Research in mathematical logic com ...
. It uses a formal approach to study reasoning: it replaces concrete expressions with abstract symbols to examine the logical form of arguments independent of their concrete content. In this sense, it is topic-neutral since it is only concerned with the abstract structure of arguments and not with their concrete content.
Formal logic is interested in deductively valid arguments, for which the truth of their premises ensures the truth of their conclusion. This means that it is impossible for the premises to be true and the conclusion to be false. For valid arguments, the logical structure that leads from the premises to the conclusion follows a pattern called a rule of inference. For example, is a rule of inference according to which all arguments of the form "(1) ''p'', (2) if ''p'' then ''q'', (3) therefore ''q''" are valid, independent of what the terms ''p'' and ''q'' stand for. In this sense, formal logic can be defined as the science of valid inferences. An alternative definition sees logic as the study of logical truths. A proposition is logically true if its truth depends only on the logical vocabulary used in it. This means that it is true in all possible worlds and under all interpretations of its non-logical terms, like the claim "either it is raining, or it is not". These two definitions of formal logic are not identical, but they are closely related. For example, if the inference from ''p'' to ''q'' is deductively valid then the claim "if ''p'' then ''q''" is a logical truth.
 Formal logic uses formal languages to express and analyze arguments. They normally have a very limited vocabulary and exact syntactic rules. These rules specify how their symbols can be combined to construct sentences, so-called
Formal logic uses formal languages to express and analyze arguments. They normally have a very limited vocabulary and exact syntactic rules. These rules specify how their symbols can be combined to construct sentences, so-called well-formed formula
In mathematical logic, propositional logic and predicate logic, a well-formed formula, abbreviated WFF or wff, often simply formula, is a finite sequence of symbols from a given alphabet that is part of a formal language.
The abbreviation wf ...
s. This simplicity and exactness of formal logic make it capable of formulating precise rules of inference. They determine whether a given argument is valid. Because of the reliance on formal language, natural language arguments cannot be studied directly. Instead, they need to be translated into formal language before their validity can be assessed.
The term "logic" can also be used in a slightly different sense as a countable noun. In this sense, ''a logic'' is a logical formal system. Distinct logics differ from each other concerning the rules of inference they accept as valid and the formal languages used to express them. Starting in the late 19th century, many new formal systems have been proposed. There are disagreements about what makes a formal system a logic. For example, it has been suggested that only logically complete systems, like first-order logic, qualify as logics. For such reasons, some theorists deny that higher-order logics are logics in the strict sense.
Informal logic
When understood in a wide sense, logic encompasses both formal and informal logic. Informal logic uses non-formal criteria and standards to analyze and assess the correctness of arguments. Its main focus is on everyday discourse. Its development was prompted by difficulties in applying the insights of formal logic to natural language arguments. In this regard, it considers problems that formal logic on its own is unable to address. Both provide criteria for assessing the correctness of arguments and distinguishing them from fallacies. Many characterizations of informal logic have been suggested but there is no general agreement on its precise definition. The most literal approach sees the terms "formal" and "informal" as applying to the language used to express arguments. On this view, informal logic studies arguments that are in informal or natural language. Formal logic can only examine them indirectly by translating them first into a formal language while informal logic investigates them in their original form. On this view, the argument "Birds fly. Tweety is a bird. Therefore, Tweety flies." belongs to natural language and is examined by informal logic. But the formal translation "(1) ; (2) ; (3) " is studied by formal logic. The study of natural language arguments comes with various difficulties. For example, natural language expressions are often ambiguous, vague, and context-dependent. Another approach defines informal logic in a wide sense as the normative study of the standards, criteria, and procedures of argumentation. In this sense, it includes questions about the role of rationality,critical thinking
Critical thinking is the process of analyzing available facts, evidence, observations, and arguments to make sound conclusions or informed choices. It involves recognizing underlying assumptions, providing justifications for ideas and actions, ...
, and the psychology of argumentation.
Another characterization identifies informal logic with the study of non-deductive arguments. In this way, it contrasts with deductive reasoning examined by formal logic. Non-deductive arguments make their conclusion probable but do not ensure that it is true. An example is the inductive argument from the empirical observation that "all ravens I have seen so far are black" to the conclusion "all ravens are black".
A further approach is to define informal logic as the study of informal fallacies. Informal fallacies are incorrect arguments in which errors are present in the content and the context of the argument. A false dilemma, for example, involves an error of content by excluding viable options. This is the case in the fallacy "you are either with us or against us; you are not with us; therefore, you are against us". Some theorists state that formal logic studies the general form of arguments while informal logic studies particular instances of arguments. Another approach is to hold that formal logic only considers the role of logical constants for correct inferences while informal logic also takes the meaning of substantive concept
A concept is an abstract idea that serves as a foundation for more concrete principles, thoughts, and beliefs.
Concepts play an important role in all aspects of cognition. As such, concepts are studied within such disciplines as linguistics, ...
s into account. Further approaches focus on the discussion of logical topics with or without formal devices and on the role of epistemology
Epistemology is the branch of philosophy that examines the nature, origin, and limits of knowledge. Also called "the theory of knowledge", it explores different types of knowledge, such as propositional knowledge about facts, practical knowle ...
for the assessment of arguments.
Basic concepts
Premises, conclusions, and truth
Premises and conclusions
''Premises'' and ''conclusions'' are the basic parts of inferences or arguments and therefore play a central role in logic. In the case of a valid inference or a correct argument, the conclusion follows from the premises, or in other words, the premises support the conclusion. For instance, the premises "Mars is red" and "Mars is a planet" support the conclusion "Mars is a red planet". For most types of logic, it is accepted that premises and conclusions have to be truth-bearers. This means that they have atruth value
In logic and mathematics, a truth value, sometimes called a logical value, is a value indicating the relation of a proposition to truth, which in classical logic has only two possible values ('' true'' or '' false''). Truth values are used in ...
: they are either true or false. Contemporary philosophy generally sees them either as ''proposition
A proposition is a statement that can be either true or false. It is a central concept in the philosophy of language, semantics, logic, and related fields. Propositions are the object s denoted by declarative sentences; for example, "The sky ...
s'' or as '' sentences''. Propositions are the denotation
In linguistics and philosophy, the denotation of a word or expression is its strictly literal meaning. For instance, the English word "warm" denotes the property of having high temperature. Denotation is contrasted with other aspects of meaning in ...
s of sentences and are usually seen as abstract object
In philosophy and the arts, a fundamental distinction exists between abstract and concrete entities. While there is no universally accepted definition, common examples illustrate the difference: numbers, sets, and ideas are typically classif ...
s. For example, the English sentence "the tree is green" is different from the German sentence "der Baum ist grün" but both express the same proposition.
Propositional theories of premises and conclusions are often criticized because they rely on abstract objects. For instance, philosophical naturalists usually reject the existence of abstract objects. Other arguments concern the challenges involved in specifying the identity criteria of propositions. These objections are avoided by seeing premises and conclusions not as propositions but as sentences, i.e. as concrete linguistic objects like the symbols displayed on a page of a book. But this approach comes with new problems of its own: sentences are often context-dependent and ambiguous, meaning an argument's validity would not only depend on its parts but also on its context and on how it is interpreted. Another approach is to understand premises and conclusions in psychological terms as thoughts or judgments. This position is known as psychologism. It was discussed at length around the turn of the 20th century but it is not widely accepted today.
Internal structure
Premises and conclusions have an internal structure. As propositions or sentences, they can be either simple or complex. A complex proposition has other propositions as its constituents, which are linked to each other through propositional connectives like "and" or "if...then". Simple propositions, on the other hand, do not have propositional parts. But they can also be conceived as having an internal structure: they are made up of subpropositional parts, like singular terms and predicates. For example, the simple proposition "Mars is red" can be formed by applying the predicate "red" to the singular term "Mars". In contrast, the complex proposition "Mars is red and Venus is white" is made up of two simple propositions connected by the propositional connective "and". Whether a proposition is true depends, at least in part, on its constituents. For complex propositions formed using truth-functional propositional connectives, their truth only depends on the truth values of their parts. But this relation is more complicated in the case of simple propositions and their subpropositional parts. These subpropositional parts have meanings of their own, like referring to objects or classes of objects. Whether the simple proposition they form is true depends on their relation to reality, i.e. what the objects they refer to are like. This topic is studied by theories of reference.Logical truth
Some complex propositions are true independently of the substantive meanings of their parts. In classical logic, for example, the complex proposition "either Mars is red or Mars is not red" is true independent of whether its parts, like the simple proposition "Mars is red", are true or false. In such cases, the truth is called a logical truth: a proposition is logically true if its truth depends only on the logical vocabulary used in it. This means that it is true under all interpretations of its non-logical terms. In some modal logics, this means that the proposition is true in all possible worlds. Some theorists define logic as the study of logical truths.Truth tables
Truth table
A truth table is a mathematical table used in logic—specifically in connection with Boolean algebra, Boolean functions, and propositional calculus—which sets out the functional values of logical expressions on each of their functional arg ...
s can be used to show how logical connectives work or how the truth values of complex propositions depends on their parts. They have a column for each input variable. Each row corresponds to one possible combination of the truth values these variables can take; for truth tables presented in the English literature, the symbols "T" and "F" or "1" and "0" are commonly used as abbreviations for the truth values "true" and "false". The first columns present all the possible truth-value combinations for the input variables. Entries in the other columns present the truth values of the corresponding expressions as determined by the input values. For example, the expression uses the logical connective ( and). It could be used to express a sentence like "yesterday was Sunday and the weather was good". It is only true if both of its input variables, ("yesterday was Sunday") and ("the weather was good"), are true. In all other cases, the expression as a whole is false. Other important logical connectives are ( not), ( or), ( if...then), and ( Sheffer stroke). Given the conditional proposition , one can form truth tables of its converse , its inverse , and its contrapositive . Truth tables can also be defined for more complex expressions that use several propositional connectives.
Arguments and inferences
Logic is commonly defined in terms of arguments or inferences as the study of their correctness. An ''argument'' is a set of premises together with a conclusion. An ''inference'' is the process of reasoning from these premises to the conclusion. But these terms are often used interchangeably in logic. Arguments are correct or incorrect depending on whether their premises support their conclusion. Premises and conclusions, on the other hand, are true or false depending on whether they are in accord with reality. In formal logic, asound
In physics, sound is a vibration that propagates as an acoustic wave through a transmission medium such as a gas, liquid or solid.
In human physiology and psychology, sound is the ''reception'' of such waves and their ''perception'' by the br ...
argument is an argument that is both correct and has only true premises. Sometimes a distinction is made between simple and complex arguments. A complex argument is made up of a chain of simple arguments. This means that the conclusion of one argument acts as a premise of later arguments. For a complex argument to be successful, each link of the chain has to be successful.
deductive reasoning
Deductive reasoning is the process of drawing valid inferences. An inference is valid if its conclusion follows logically from its premises, meaning that it is impossible for the premises to be true and the conclusion to be false. For example, t ...
. But even arguments that are not deductively valid may still be good arguments because their premises offer non-deductive support to their conclusions. For such cases, the term ''ampliative'' or ''inductive reasoning'' is used. Deductive arguments are associated with formal logic in contrast to the relation between ampliative arguments and informal logic.
Deductive
A deductively valid argument is one whose premises guarantee the truth of its conclusion. For instance, the argument "(1) all frogs are amphibians; (2) no cats are amphibians; (3) therefore no cats are frogs" is deductively valid. For deductive validity, it does not matter whether the premises or the conclusion are actually true. So the argument "(1) all frogs are mammals; (2) no cats are mammals; (3) therefore no cats are frogs" is also valid because the conclusion follows necessarily from the premises. According to an influential view byAlfred Tarski
Alfred Tarski (; ; born Alfred Teitelbaum;School of Mathematics and Statistics, University of St Andrews ''School of Mathematics and Statistics, University of St Andrews''. January 14, 1901 – October 26, 1983) was a Polish-American logician ...
, deductive arguments have three essential features: (1) they are formal, i.e. they depend only on the form of the premises and the conclusion; (2) they are a priori, i.e. no sense experience is needed to determine whether they obtain; (3) they are modal, i.e. that they hold by logical necessity for the given propositions, independent of any other circumstances.
Because of the first feature, the focus on formality, deductive inference is usually identified with rules of inference. Rules of inference specify the form of the premises and the conclusion: how they have to be structured for the inference to be valid. Arguments that do not follow any rule of inference are deductively invalid. The is a prominent rule of inference. It has the form "''p''; if ''p'', then ''q''; therefore ''q''". Knowing that it has just rained () and that after rain the streets are wet (), one can use to deduce that the streets are wet ().
The third feature can be expressed by stating that deductively valid inferences are truth-preserving: it is impossible for the premises to be true and the conclusion to be false. Because of this feature, it is often asserted that deductive inferences are uninformative since the conclusion cannot arrive at new information not already present in the premises. But this point is not always accepted since it would mean, for example, that most of mathematics is uninformative. A different characterization distinguishes between surface and depth information. The surface information of a sentence is the information it presents explicitly. Depth information is the totality of the information contained in the sentence, both explicitly and implicitly. According to this view, deductive inferences are uninformative on the depth level. But they can be highly informative on the surface level by making implicit information explicit. This happens, for example, in mathematical proofs.
Ampliative
Ampliative arguments are arguments whose conclusions contain additional information not found in their premises. In this regard, they are more interesting since they contain information on the depth level and the thinker may learn something genuinely new. But this feature comes with a certain cost: the premises support the conclusion in the sense that they make its truth more likely but they do not ensure its truth. This means that the conclusion of an ampliative argument may be false even though all its premises are true. This characteristic is closely related to '' non-monotonicity'' and '' defeasibility'': it may be necessary to retract an earlier conclusion upon receiving new information or in light of new inferences drawn. Ampliative reasoning plays a central role in many arguments found in everyday discourse and the sciences. Ampliative arguments are not automatically incorrect. Instead, they just follow different standards of correctness. The support they provide for their conclusion usually comes in degrees. This means that strong ampliative arguments make their conclusion very likely while weak ones are less certain. As a consequence, the line between correct and incorrect arguments is blurry in some cases, such as when the premises offer weak but non-negligible support. This contrasts with deductive arguments, which are either valid or invalid with nothing in-between. The terminology used to categorize ampliative arguments is inconsistent. Some authors, like James Hawthorne, use the term " induction" to cover all forms of non-deductive arguments. But in a more narrow sense, ''induction'' is only one type of ampliative argument alongside '' abductive arguments''. Some philosophers, like Leo Groarke, also allow ''conductive arguments'' as another type. In this narrow sense, induction is often defined as a form of statistical generalization. In this case, the premises of an inductive argument are many individual observations that all show a certain pattern. The conclusion then is a general law that this pattern always obtains. In this sense, one may infer that "all elephants are gray" based on one's past observations of the color of elephants. A closely related form of inductive inference has as its conclusion not a general law but one more specific instance, as when it is inferred that an elephant one has not seen yet is also gray. Some theorists, like Igor Douven, stipulate that inductive inferences rest only on statistical considerations. This way, they can be distinguished from abductive inference. Abductive inference may or may not take statistical observations into consideration. In either case, the premises offer support for the conclusion because the conclusion is the best explanation of why the premises are true. In this sense, abduction is also called the ''inference to the best explanation''. For example, given the premise that there is a plate with breadcrumbs in the kitchen in the early morning, one may infer the conclusion that one's house-mate had a midnight snack and was too tired to clean the table. This conclusion is justified because it is the best explanation of the current state of the kitchen. For abduction, it is not sufficient that the conclusion explains the premises. For example, the conclusion that a burglar broke into the house last night, got hungry on the job, and had a midnight snack, would also explain the state of the kitchen. But this conclusion is not justified because it is not the best or most likely explanation.Fallacies
Not all arguments live up to the standards of correct reasoning. When they do not, they are usually referred to asfallacies
A fallacy is the use of invalid or otherwise faulty reasoning in the construction of an argument that may appear to be well-reasoned if unnoticed. The term was introduced in the Western intellectual tradition by the Aristotelian '' De Sophis ...
. Their central aspect is not that their conclusion is false but that there is some flaw with the reasoning leading to this conclusion. So the argument "it is sunny today; therefore spiders have eight legs" is fallacious even though the conclusion is true. Some theorists, like John Stuart Mill
John Stuart Mill (20 May 1806 – 7 May 1873) was an English philosopher, political economist, politician and civil servant. One of the most influential thinkers in the history of liberalism and social liberalism, he contributed widely to s ...
, give a more restrictive definition of fallacies by additionally requiring that they appear to be correct. This way, genuine fallacies can be distinguished from mere mistakes of reasoning due to carelessness. This explains why people tend to commit fallacies: because they have an alluring element that seduces people into committing and accepting them. However, this reference to appearances is controversial because it belongs to the field of psychology
Psychology is the scientific study of mind and behavior. Its subject matter includes the behavior of humans and nonhumans, both consciousness, conscious and Unconscious mind, unconscious phenomena, and mental processes such as thoughts, feel ...
, not logic, and because appearances may be different for different people.
Fallacies are usually divided into formal and informal fallacies. For formal fallacies, the source of the error is found in the ''form'' of the argument. For example, denying the antecedent is one type of formal fallacy, as in "if Othello is a bachelor, then he is male; Othello is not a bachelor; therefore Othello is not male". But most fallacies fall into the category of informal fallacies, of which a great variety is discussed in the academic literature. The source of their error is usually found in the ''content'' or the ''context'' of the argument. Informal fallacies are sometimes categorized as fallacies of ambiguity, fallacies of presumption, or fallacies of relevance. For fallacies of ambiguity, the ambiguity and vagueness of natural language are responsible for their flaw, as in "feathers are light; what is light cannot be dark; therefore feathers cannot be dark". Fallacies of presumption have a wrong or unjustified premise but may be valid otherwise. In the case of fallacies of relevance, the premises do not support the conclusion because they are not relevant to it.
Definitory and strategic rules
The main focus of most logicians is to study the criteria according to which an argument is correct or incorrect. A fallacy is committed if these criteria are violated. In the case of formal logic, they are known as ''rules of inference''. They are definitory rules, which determine whether an inference is correct or which inferences are allowed. Definitory rules contrast with strategic rules. Strategic rules specify which inferential moves are necessary to reach a given conclusion based on a set of premises. This distinction does not just apply to logic but also to games. Inchess
Chess is a board game for two players. It is an abstract strategy game that involves Perfect information, no hidden information and no elements of game of chance, chance. It is played on a square chessboard, board consisting of 64 squares arran ...
, for example, the definitory rules dictate that bishops
A bishop is an ordained member of the clergy who is entrusted with a position of Episcopal polity, authority and oversight in a religious institution. In Christianity, bishops are normally responsible for the governance and administration of di ...
may only move diagonally. The strategic rules, on the other hand, describe how the allowed moves may be used to win a game, for instance, by controlling the center and by defending one's king
King is a royal title given to a male monarch. A king is an Absolute monarchy, absolute monarch if he holds unrestricted Government, governmental power or exercises full sovereignty over a nation. Conversely, he is a Constitutional monarchy, ...
. It has been argued that logicians should give more emphasis to strategic rules since they are highly relevant for effective reasoning.
Formal systems
A formal system of logic consists of a formal language together with a set ofaxiom
An axiom, postulate, or assumption is a statement that is taken to be true, to serve as a premise or starting point for further reasoning and arguments. The word comes from the Ancient Greek word (), meaning 'that which is thought worthy or ...
s and a proof system used to draw inferences from these axioms. In logic, axioms are statements that are accepted without proof. They are used to justify other statements. Some theorists also include a semantics
Semantics is the study of linguistic Meaning (philosophy), meaning. It examines what meaning is, how words get their meaning, and how the meaning of a complex expression depends on its parts. Part of this process involves the distinction betwee ...
that specifies how the expressions of the formal language relate to real objects. Starting in the late 19th century, many new formal systems have been proposed.
A ''formal language'' consists of an ''alphabet'' and syntactic rules. The alphabet is the set of basic symbols used in expressions. The syntactic rules determine how these symbols may be arranged to result in well-formed formulas. For instance, the syntactic rules of propositional logic determine that is a well-formed formula but is not since the logical conjunction requires terms on both sides.
A ''proof system'' is a collection of rules to construct formal proofs. It is a tool to arrive at conclusions from a set of axioms. Rules in a proof system are defined in terms of the syntactic form of formulas independent of their specific content. For instance, the classical rule of conjunction introduction states that follows from the premises and . Such rules can be applied sequentially, giving a mechanical procedure for generating conclusions from premises. There are different types of proof systems including natural deduction and sequent calculi.
A ''semantics'' is a system for mapping expressions of a formal language to their denotations. In many systems of logic, denotations are truth values. For instance, the semantics for classical propositional logic assigns the formula the denotation "true" whenever and are true. From the semantic point of view, a premise entails a conclusion if the conclusion is true whenever the premise is true.
A system of logic is sound
In physics, sound is a vibration that propagates as an acoustic wave through a transmission medium such as a gas, liquid or solid.
In human physiology and psychology, sound is the ''reception'' of such waves and their ''perception'' by the br ...
when its proof system cannot derive a conclusion from a set of premises unless it is semantically entailed by them. In other words, its proof system cannot lead to false conclusions, as defined by the semantics. A system is complete when its proof system can derive every conclusion that is semantically entailed by its premises. In other words, its proof system can lead to any true conclusion, as defined by the semantics. Thus, soundness and completeness together describe a system whose notions of validity and entailment line up perfectly.
Systems of logic
Systems of logic are theoretical frameworks for assessing the correctness of reasoning and arguments. For over two thousand years,Aristotelian logic
In logic and formal semantics, term logic, also known as traditional logic, syllogistic logic or Aristotelian logic, is a loose name for an approach to formal logic that began with Aristotle and was developed further in ancient history mostly b ...
was treated as the canon of logic in the Western world, but modern developments in this field have led to a vast proliferation of logical systems. One prominent categorization divides modern formal logical systems into classical logic
Classical logic (or standard logic) or Frege–Russell logic is the intensively studied and most widely used class of deductive logic. Classical logic has had much influence on analytic philosophy.
Characteristics
Each logical system in this c ...
, extended logics, and deviant logics.
Aristotelian
Aristotelian logic
In logic and formal semantics, term logic, also known as traditional logic, syllogistic logic or Aristotelian logic, is a loose name for an approach to formal logic that began with Aristotle and was developed further in ancient history mostly b ...
encompasses a great variety of topics. They include metaphysical
Metaphysics is the branch of philosophy that examines the basic structure of reality. It is traditionally seen as the study of mind-independent features of the world, but some theorists view it as an inquiry into the conceptual framework of h ...
theses about ontological categories and problems of scientific explanation. But in a more narrow sense, it is identical to term logic or syllogistics. A syllogism is a form of argument involving three propositions: two premises and a conclusion. Each proposition has three essential parts: a subject, a predicate, and a copula connecting the subject to the predicate. For example, the proposition "Socrates is wise" is made up of the subject "Socrates", the predicate "wise", and the copula "is". The subject and the predicate are the ''terms'' of the proposition. Aristotelian logic does not contain complex propositions made up of simple propositions. It differs in this aspect from propositional logic, in which any two propositions can be linked using a logical connective like "and" to form a new complex proposition.
In Aristotelian logic, the subject can be ''universal'', ''particular'', ''indefinite'', or ''singular''. For example, the term "all humans" is a universal subject in the proposition "all humans are mortal". A similar proposition could be formed by replacing it with the particular term "some humans", the indefinite term "a human", or the singular term "Socrates".
Aristotelian logic only includes predicates for simple properties of entities. But it lacks predicates corresponding to relations between entities. The predicate can be linked to the subject in two ways: either by affirming it or by denying it. For example, the proposition "Socrates is not a cat" involves the denial of the predicate "cat" to the subject "Socrates". Using combinations of subjects and predicates, a great variety of propositions and syllogisms can be formed. Syllogisms are characterized by the fact that the premises are linked to each other and to the conclusion by sharing one term in each case. Thus, these three propositions contain three terms, referred to as ''major term'', ''minor term'', and ''middle term''. The central aspect of Aristotelian logic involves classifying all possible syllogisms into valid and invalid arguments according to how the propositions are formed. For example, the syllogism "all men are mortal; Socrates is a man; therefore Socrates is mortal" is valid. The syllogism "all cats are mortal; Socrates is mortal; therefore Socrates is a cat", on the other hand, is invalid.
Classical
Classical logic
Classical logic (or standard logic) or Frege–Russell logic is the intensively studied and most widely used class of deductive logic. Classical logic has had much influence on analytic philosophy.
Characteristics
Each logical system in this c ...
is distinct from traditional or Aristotelian logic. It encompasses propositional logic and first-order logic. It is "classical" in the sense that it is based on basic logical intuitions shared by most logicians. These intuitions include the law of excluded middle, the double negation elimination, the principle of explosion, and the bivalence of truth. It was originally developed to analyze mathematical arguments and was only later applied to other fields as well. Because of this focus on mathematics, it does not include logical vocabulary relevant to many other topics of philosophical importance. Examples of concepts it overlooks are the contrast between necessity and possibility and the problem of ethical obligation and permission. Similarly, it does not address the relations between past, present, and future. Such issues are addressed by extended logics. They build on the basic intuitions of classical logic and expand it by introducing new logical vocabulary. This way, the exact logical approach is applied to fields like ethics
Ethics is the philosophy, philosophical study of Morality, moral phenomena. Also called moral philosophy, it investigates Normativity, normative questions about what people ought to do or which behavior is morally right. Its main branches inclu ...
or epistemology that lie beyond the scope of mathematics.
Propositional logic
Propositional logic comprises formal systems in which formulae are built from atomic propositions using logical connectives. For instance, propositional logic represents the conjunction of two atomic propositions and as the complex formula . Unlike predicate logic where terms and predicates are the smallest units, propositional logic takes full propositions with truth values as its most basic component. Thus, propositional logics can only represent logical relationships that arise from the way complex propositions are built from simpler ones. But it cannot represent inferences that result from the inner structure of a proposition.First-order logic
Extended
Extended logics are logical systems that accept the basic principles of classical logic. They introduce additional symbols and principles to apply it to fields likemetaphysics
Metaphysics is the branch of philosophy that examines the basic structure of reality. It is traditionally seen as the study of mind-independent features of the world, but some theorists view it as an inquiry into the conceptual framework of ...
, ethics
Ethics is the philosophy, philosophical study of Morality, moral phenomena. Also called moral philosophy, it investigates Normativity, normative questions about what people ought to do or which behavior is morally right. Its main branches inclu ...
, and epistemology
Epistemology is the branch of philosophy that examines the nature, origin, and limits of knowledge. Also called "the theory of knowledge", it explores different types of knowledge, such as propositional knowledge about facts, practical knowle ...
.
Modal logic
Modal logic is an extension of classical logic. In its original form, sometimes called "alethic modal logic", it introduces two new symbols: expresses that something is possible while expresses that something is necessary. For example, if the formula stands for the sentence "Socrates is a banker" then the formula articulates the sentence "It is possible that Socrates is a banker". To include these symbols in the logical formalism, modal logic introduces new rules of inference that govern what role they play in inferences. One rule of inference states that, if something is necessary, then it is also possible. This means that follows from . Another principle states that if a proposition is necessary then its negation is impossible and vice versa. This means that is equivalent to . Other forms of modal logic introduce similar symbols but associate different meanings with them to apply modal logic to other fields. For example, deontic logic concerns the field of ethics and introduces symbols to express the ideas of obligation and permission, i.e. to describe whether an agent has to perform a certain action or is allowed to perform it. The modal operators in temporal modal logic articulate temporal relations. They can be used to express, for example, that something happened at one time or that something is happening all the time. In epistemology, epistemic modal logic is used to represent the ideas of knowing something in contrast to merely believing it to be the case.Higher order logic
Higher-order logics extend classical logic not by using modal operators but by introducing new forms of quantification. Quantifiers correspond to terms like "all" or "some". In classical first-order logic, quantifiers are only applied to individuals. The formula (some apples are sweet) is an example of the existential quantifier applied to the individual variable . In higher-order logics, quantification is also allowed over predicates. This increases its expressive power. For example, to express the idea that Mary and John share some qualities, one could use the formula . In this case, the existential quantifier is applied to the predicate variable . The added expressive power is especially useful for mathematics since it allows for more succinct formulations of mathematical theories. But it has drawbacks in regard to its meta-logical properties and ontological implications, which is why first-order logic is still more commonly used.Deviant
Deviant logics are logical systems that reject some of the basic intuitions of classical logic. Because of this, they are usually seen not as its supplements but as its rivals. Deviant logical systems differ from each other either because they reject different classical intuitions or because they propose different alternatives to the same issue. Intuitionistic logic is a restricted version of classical logic. It uses the same symbols but excludes some rules of inference. For example, according to the law of double negation elimination, if a sentence is not not true, then it is true. This means that follows from . This is a valid rule of inference in classical logic but it is invalid in intuitionistic logic. Another classical principle not part of intuitionistic logic is the law of excluded middle. It states that for every sentence, either it or its negation is true. This means that every proposition of the form is true. These deviations from classical logic are based on the idea that truth is established by verification using a proof. Intuitionistic logic is especially prominent in the field of constructive mathematics, which emphasizes the need to find or construct a specific example to prove its existence. Multi-valued logics depart from classicality by rejecting the principle of bivalence, which requires all propositions to be either true or false. For instance,Jan Łukasiewicz
Jan Łukasiewicz (; 21 December 1878 – 13 February 1956) was a Polish logician and philosopher who is best known for Polish notation and Łukasiewicz logic. His work centred on philosophical logic, mathematical logic and history of logi ...
and Stephen Cole Kleene both proposed ternary logics which have a third truth value representing that a statement's truth value is indeterminate. These logics have been applied in the field of linguistics. Fuzzy logics are multivalued logics that have an infinite number of "degrees of truth", represented by a real number
In mathematics, a real number is a number that can be used to measure a continuous one- dimensional quantity such as a duration or temperature. Here, ''continuous'' means that pairs of values can have arbitrarily small differences. Every re ...
between 0 and 1.
Paraconsistent logics are logical systems that can deal with contradictions. They are formulated to avoid the principle of explosion: for them, it is not the case that anything follows from a contradiction. They are often motivated by dialetheism, the view that contradictions are real or that reality itself is contradictory. Graham Priest is an influential contemporary proponent of this position and similar views have been ascribed to Georg Wilhelm Friedrich Hegel
Georg Wilhelm Friedrich Hegel (27 August 1770 – 14 November 1831) was a 19th-century German idealist. His influence extends across a wide range of topics from metaphysical issues in epistemology and ontology, to political philosophy and t ...
.
Informal
Informal logic
Informal logic encompasses the principles of logic and logical thought outside of a formal setting (characterized by the usage of particular statements). However, the precise definition of "informal logic" is a matter of some dispute. Ralph H. ...
is usually carried out in a less systematic way. It often focuses on more specific issues, like investigating a particular type of fallacy or studying a certain aspect of argumentation. Nonetheless, some frameworks of informal logic have also been presented that try to provide a systematic characterization of the correctness of arguments.
The ''pragmatic'' or ''dialogical approach'' to informal logic sees arguments as speech acts and not merely as a set of premises together with a conclusion. As speech acts, they occur in a certain context, like a dialogue, which affects the standards of right and wrong arguments. A prominent version by Douglas N. Walton understands a dialogue as a game between two players. The initial position of each player is characterized by the propositions to which they are committed and the conclusion they intend to prove. Dialogues are games of persuasion: each player has the goal of convincing the opponent of their own conclusion. This is achieved by making arguments: arguments are the moves of the game. They affect to which propositions the players are committed. A winning move is a successful argument that takes the opponent's commitments as premises and shows how one's own conclusion follows from them. This is usually not possible straight away. For this reason, it is normally necessary to formulate a sequence of arguments as intermediary steps, each of which brings the opponent a little closer to one's intended conclusion. Besides these positive arguments leading one closer to victory, there are also negative arguments preventing the opponent's victory by denying their conclusion. Whether an argument is correct depends on whether it promotes the progress of the dialogue. Fallacies, on the other hand, are violations of the standards of proper argumentative rules. These standards also depend on the type of dialogue. For example, the standards governing the scientific discourse differ from the standards in business negotiations.
The ''epistemic approach'' to informal logic, on the other hand, focuses on the epistemic role of arguments. It is based on the idea that arguments aim to increase our knowledge. They achieve this by linking justified beliefs to beliefs that are not yet justified. Correct arguments succeed at expanding knowledge while fallacies are epistemic failures: they do not justify the belief in their conclusion. For example, the fallacy of begging the question is a ''fallacy'' because it fails to provide independent justification for its conclusion, even though it is deductively valid. In this sense, logical normativity consists in epistemic success or rationality. The Bayesian approach is one example of an epistemic approach. Central to Bayesianism is not just whether the agent believes something but the degree to which they believe it, the so-called ''credence''. Degrees of belief are seen as subjective probabilities in the believed proposition, i.e. how certain the agent is that the proposition is true. On this view, reasoning can be interpreted as a process of changing one's credences, often in reaction to new incoming information. Correct reasoning and the arguments it is based on follow the laws of probability, for example, the principle of conditionalization. Bad or irrational reasoning, on the other hand, violates these laws.
Areas of research
Logic is studied in various fields. In many cases, this is done by applying its formal method to specific topics outside its scope, like to ethics or computer science. In other cases, logic itself is made the subject of research in another discipline. This can happen in diverse ways. For instance, it can involve investigating the philosophical assumptions linked to the basic concepts used by logicians. Other ways include interpreting and analyzing logic through mathematical structures as well as studying and comparing abstract properties of formal logical systems.Philosophy of logic and philosophical logic
''Philosophy of logic'' is the philosophical discipline studying the scope and nature of logic. It examines many presuppositions implicit in logic, like how to define its basic concepts or the metaphysical assumptions associated with them. It is also concerned with how to classify logical systems and considers the ontological commitments they incur. ''Philosophical logic'' is one of the areas within the philosophy of logic. It studies the application of logical methods to philosophical problems in fields like metaphysics, ethics, and epistemology. This application usually happens in the form of extended or deviant logical systems.Metalogic
Metalogic is the field of inquiry studying the properties of formal logical systems. For example, when a new formal system is developed, metalogicians may study it to determine which formulas can be proven in it. They may also study whether analgorithm
In mathematics and computer science, an algorithm () is a finite sequence of Rigour#Mathematics, mathematically rigorous instructions, typically used to solve a class of specific Computational problem, problems or to perform a computation. Algo ...
could be developed to find a proof for each formula and whether every provable formula in it is a tautology. Finally, they may compare it to other logical systems to understand its distinctive features. A key issue in metalogic concerns the relation between syntax and semantics. The syntactic rules of a formal system determine how to deduce conclusions from premises, i.e. how to formulate proofs. The semantics of a formal system governs which sentences are true and which ones are false. This determines the validity of arguments since, for valid arguments, it is impossible for the premises to be true and the conclusion to be false. The relation between syntax and semantics concerns issues like whether every valid argument is provable and whether every provable argument is valid. Metalogicians also study whether logical systems are complete, sound, and consistent. They are interested in whether the systems are decidable and what expressive power they have. Metalogicians usually rely heavily on abstract mathematical reasoning when examining and formulating metalogical proofs. This way, they aim to arrive at precise and general conclusions on these topics.
Mathematical logic
 The term "mathematical logic" is sometimes used as a synonym of "formal logic". But in a more restricted sense, it refers to the study of logic within mathematics. Major subareas include
The term "mathematical logic" is sometimes used as a synonym of "formal logic". But in a more restricted sense, it refers to the study of logic within mathematics. Major subareas include model theory
In mathematical logic, model theory is the study of the relationship between theory (mathematical logic), formal theories (a collection of Sentence (mathematical logic), sentences in a formal language expressing statements about a Structure (mat ...
, proof theory
Proof theory is a major branchAccording to , proof theory is one of four domains mathematical logic, together with model theory, axiomatic set theory, and recursion theory. consists of four corresponding parts, with part D being about "Proof The ...
, set theory
Set theory is the branch of mathematical logic that studies Set (mathematics), sets, which can be informally described as collections of objects. Although objects of any kind can be collected into a set, set theory – as a branch of mathema ...
, and computability theory
Computability theory, also known as recursion theory, is a branch of mathematical logic, computer science, and the theory of computation that originated in the 1930s with the study of computable functions and Turing degrees. The field has since ex ...
. Research in mathematical logic commonly addresses the mathematical properties of formal systems of logic. However, it can also include attempts to use logic to analyze mathematical reasoning or to establish logic-based foundations of mathematics
Foundations of mathematics are the mathematical logic, logical and mathematics, mathematical framework that allows the development of mathematics without generating consistency, self-contradictory theories, and to have reliable concepts of theo ...
. The latter was a major concern in early 20th-century mathematical logic, which pursued the program of logicism pioneered by philosopher-logicians such as Gottlob Frege, Alfred North Whitehead, and Bertrand Russell
Bertrand Arthur William Russell, 3rd Earl Russell, (18 May 1872 – 2 February 1970) was a British philosopher, logician, mathematician, and public intellectual. He had influence on mathematics, logic, set theory, and various areas of analytic ...
. Mathematical theories were supposed to be logical tautologies, and their program was to show this by means of a reduction of mathematics to logic. Many attempts to realize this program failed, from the crippling of Frege's project in his ' by Russell's paradox, to the defeat of Hilbert's program by Gödel's incompleteness theorems.
Set theory originated in the study of the infinite by Georg Cantor
Georg Ferdinand Ludwig Philipp Cantor ( ; ; – 6 January 1918) was a mathematician who played a pivotal role in the creation of set theory, which has become a foundations of mathematics, fundamental theory in mathematics. Cantor establi ...
, and it has been the source of many of the most challenging and important issues in mathematical logic. They include Cantor's theorem, the status of the Axiom of Choice, the question of the independence of the continuum hypothesis, and the modern debate on large cardinal axioms.
Computability theory is the branch of mathematical logic that studies effective procedures to solve calculation problems. One of its main goals is to understand whether it is possible to solve a given problem using an algorithm. For instance, given a certain claim about the positive integers, it examines whether an algorithm can be found to determine if this claim is true. Computability theory uses various theoretical tools and models, such as Turing machines, to explore this type of issue.
Computational logic
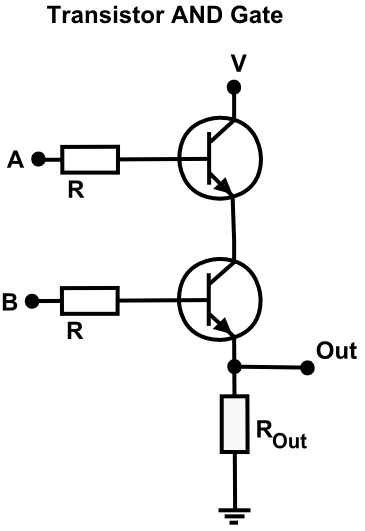
 Computational logic is the branch of logic and
Computational logic is the branch of logic and computer science
Computer science is the study of computation, information, and automation. Computer science spans Theoretical computer science, theoretical disciplines (such as algorithms, theory of computation, and information theory) to Applied science, ...
that studies how to implement mathematical reasoning and logical formalisms using computers. This includes, for example, automatic theorem provers, which employ rules of inference to construct a proof step by step from a set of premises to the intended conclusion without human intervention. Logic programming languages are designed specifically to express facts using logical formulas and to draw inferences from these facts. For example, Prolog
Prolog is a logic programming language that has its origins in artificial intelligence, automated theorem proving, and computational linguistics.
Prolog has its roots in first-order logic, a formal logic. Unlike many other programming language ...
is a logic programming language based on predicate logic. Computer scientists also apply concepts from logic to problems in computing. The works of Claude Shannon
Claude Elwood Shannon (April 30, 1916 – February 24, 2001) was an American mathematician, electrical engineer, computer scientist, cryptographer and inventor known as the "father of information theory" and the man who laid the foundations of th ...
were influential in this regard. He showed how Boolean logic
In mathematics and mathematical logic, Boolean algebra is a branch of algebra. It differs from elementary algebra in two ways. First, the values of the variable (mathematics), variables are the truth values ''true'' and ''false'', usually denot ...
can be used to understand and implement computer circuits. This can be achieved using electronic logic gates
A logic gate is a device that performs a Boolean function, a logical operation performed on one or more Binary number, binary inputs that produces a single binary output. Depending on the context, the term may refer to an ideal logic gate, one ...
, i.e. electronic circuits with one or more inputs and usually one output. The truth values of propositions are represented by voltage levels. In this way, logic functions can be simulated by applying the corresponding voltages to the inputs of the circuit and determining the value of the function by measuring the voltage of the output.
Formal semantics of natural language
Formal semantics is a subfield of logic,linguistics
Linguistics is the scientific study of language. The areas of linguistic analysis are syntax (rules governing the structure of sentences), semantics (meaning), Morphology (linguistics), morphology (structure of words), phonetics (speech sounds ...
, and the philosophy of language
Philosophy of language refers to the philosophical study of the nature of language. It investigates the relationship between language, language users, and the world. Investigations may include inquiry into the nature of Meaning (philosophy), me ...
. The discipline of semantics
Semantics is the study of linguistic Meaning (philosophy), meaning. It examines what meaning is, how words get their meaning, and how the meaning of a complex expression depends on its parts. Part of this process involves the distinction betwee ...
studies the meaning of language. Formal semantics uses formal tools from the fields of symbolic logic and mathematics to give precise theories of the meaning of natural language expressions. It understands meaning usually in relation to truth conditions, i.e. it examines in which situations a sentence would be true or false. One of its central methodological assumptions is the principle of compositionality. It states that the meaning of a complex expression is determined by the meanings of its parts and how they are combined. For example, the meaning of the verb phrase "walk and sing" depends on the meanings of the individual expressions "walk" and "sing". Many theories in formal semantics rely on model theory. This means that they employ set theory to construct a model and then interpret the meanings of expression in relation to the elements in this model. For example, the term "walk" may be interpreted as the set of all individuals in the model that share the property of walking. Early influential theorists in this field were Richard Montague and Barbara Partee, who focused their analysis on the English language.
Epistemology of logic
The epistemology of logic studies how one knows that an argument is valid or that a proposition is logically true. This includes questions like how to justify that is a valid rule of inference or that contradictions are false. The traditionally dominant view is that this form of logical understanding belongs to knowledgea priori
('from the earlier') and ('from the later') are Latin phrases used in philosophy to distinguish types of knowledge, Justification (epistemology), justification, or argument by their reliance on experience. knowledge is independent from any ...
. In this regard, it is often argued that the mind
The mind is that which thinks, feels, perceives, imagines, remembers, and wills. It covers the totality of mental phenomena, including both conscious processes, through which an individual is aware of external and internal circumstances ...
has a special faculty to examine relations between pure ideas and that this faculty is also responsible for apprehending logical truths. A similar approach understands the rules of logic in terms of linguistic conventions. On this view, the laws of logic are trivial since they are true by definition: they just express the meanings of the logical vocabulary.
Some theorists, like Hilary Putnam
Hilary Whitehall Putnam (; July 31, 1926 – March 13, 2016) was an American philosopher, mathematician, computer scientist, and figure in analytic philosophy in the second half of the 20th century. He contributed to the studies of philosophy of ...
and Penelope Maddy, object to the view that logic is knowable a priori. They hold instead that logical truths depend on the empirical
Empirical evidence is evidence obtained through sense experience or experimental procedure. It is of central importance to the sciences and plays a role in various other fields, like epistemology and law.
There is no general agreement on how t ...
world. This is usually combined with the claim that the laws of logic express universal regularities found in the structural features of the world. According to this view, they may be explored by studying general patterns of the fundamental sciences. For example, it has been argued that certain insights of quantum mechanics
Quantum mechanics is the fundamental physical Scientific theory, theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is ...
refute the principle of distributivity in classical logic, which states that the formula is equivalent to . This claim can be used as an empirical argument for the thesis that quantum logic is the correct logical system and should replace classical logic.
History
Logic was developed independently in several cultures during antiquity. One major early contributor wasAristotle
Aristotle (; 384–322 BC) was an Ancient Greek philosophy, Ancient Greek philosopher and polymath. His writings cover a broad range of subjects spanning the natural sciences, philosophy, linguistics, economics, politics, psychology, a ...
, who developed ''term logic'' in his '' Organon'' and '' Prior Analytics''. He was responsible for the introduction of the hypothetical syllogism and temporal modal logic. Further innovations include inductive logic as well as the discussion of new logical concepts such as terms, predicables, syllogisms, and propositions. Aristotelian logic was highly regarded in classical and medieval times, both in Europe and the Middle East. It remained in wide use in the West until the early 19th century. It has now been superseded by later work, though many of its key insights are still present in modern systems of logic.
Ibn Sina (Avicenna) was the founder of Avicennian logic, which replaced Aristotelian logic as the dominant system of logic in the Islamic world. It influenced Western medieval writers such as Albertus Magnus and William of Ockham. Ibn Sina wrote on the hypothetical syllogism and on the propositional calculus
The propositional calculus is a branch of logic. It is also called propositional logic, statement logic, sentential calculus, sentential logic, or sometimes zeroth-order logic. Sometimes, it is called ''first-order'' propositional logic to contra ...
. He developed an original "temporally modalized" syllogistic theory, involving temporal logic and modal logic. He also made use of inductive logic, such as his methods of agreement, difference, and concomitant variation, which are critical to the scientific method
The scientific method is an Empirical evidence, empirical method for acquiring knowledge that has been referred to while doing science since at least the 17th century. Historically, it was developed through the centuries from the ancient and ...
. Fakhr al-Din al-Razi was another influential Muslim logician. He criticized Aristotelian syllogistics and formulated an early system of inductive logic, foreshadowing the system of inductive logic developed by John Stuart Mill.
During the Middle Ages
In the history of Europe, the Middle Ages or medieval period lasted approximately from the 5th to the late 15th centuries, similarly to the post-classical period of global history. It began with the fall of the Western Roman Empire and ...
, many translations and interpretations of Aristotelian logic were made. The works of Boethius
Anicius Manlius Severinus Boethius, commonly known simply as Boethius (; Latin: ''Boetius''; 480–524 AD), was a Roman Roman Senate, senator, Roman consul, consul, ''magister officiorum'', polymath, historian, and philosopher of the Early Middl ...
were particularly influential. Besides translating Aristotle's work into Latin, he also produced textbooks on logic. Later, the works of Islamic philosophers such as Ibn Sina and Ibn Rushd (Averroes) were drawn on. This expanded the range of ancient works available to medieval Christian scholars since more Greek work was available to Muslim scholars that had been preserved in Latin commentaries. In 1323, William of Ockham's influential ' was released. It is a comprehensive treatise on logic that discusses many basic concepts of logic and provides a systematic exposition of types of propositions and their truth conditions.
In Chinese philosophy, the School of Names and Mohism were particularly influential. The School of Names focused on the use of language and on paradoxes. For example, Gongsun Long proposed the white horse paradox, which defends the thesis that a white horse is not a horse. The school of Mohism also acknowledged the importance of language for logic and tried to relate the ideas in these fields to the realm of ethics.
In India, the study of logic was primarily pursued by the schools of Nyaya, Buddhism
Buddhism, also known as Buddhadharma and Dharmavinaya, is an Indian religion and List of philosophies, philosophical tradition based on Pre-sectarian Buddhism, teachings attributed to the Buddha, a wandering teacher who lived in the 6th or ...
, and Jainism
Jainism ( ), also known as Jain Dharma, is an Indian religions, Indian religion whose three main pillars are nonviolence (), asceticism (), and a rejection of all simplistic and one-sided views of truth and reality (). Jainism traces its s ...
. It was not treated as a separate academic discipline and discussions of its topics usually happened in the context of epistemology and theories of dialogue or argumentation. In Nyaya, inference is understood as a source of knowledge (). It follows the perception of an object and tries to arrive at conclusions, for example, about the cause of this object. A similar emphasis on the relation to epistemology is also found in Buddhist and Jainist schools of logic, where inference is used to expand the knowledge gained through other sources. Some of the later theories of Nyaya, belonging to the Navya-Nyāya school, resemble modern forms of logic, such as Gottlob Frege's distinction between sense and reference and his definition of number.
The syllogistic logic developed by Aristotle predominated in the West until the mid-19th century, when interest in the foundations of mathematics stimulated the development of modern symbolic logic. Many see Gottlob Frege's ' as the birthplace of modern logic. Gottfried Wilhelm Leibniz
Gottfried Wilhelm Leibniz (or Leibnitz; – 14 November 1716) was a German polymath active as a mathematician, philosopher, scientist and diplomat who is credited, alongside Sir Isaac Newton, with the creation of calculus in addition to ...
's idea of a universal formal language is often considered a forerunner. Other pioneers were George Boole
George Boole ( ; 2 November 1815 – 8 December 1864) was a largely self-taught English mathematician, philosopher and logician, most of whose short career was spent as the first professor of mathematics at Queen's College, Cork in Ireland. H ...
, who invented Boolean algebra as a mathematical system of logic, and Charles Peirce, who developed the logic of relatives. Alfred North Whitehead and Bertrand Russell, in turn, condensed many of these insights in their work '. Modern logic introduced novel concepts, such as functions, quantifiers, and relational predicates. A hallmark of modern symbolic logic is its use of formal language to precisely codify its insights. In this regard, it departs from earlier logicians, who relied mainly on natural language. Of particular influence was the development of first-order logic, which is usually treated as the standard system of modern logic. Its analytical generality allowed the formalization of mathematics and drove the investigation of set theory
Set theory is the branch of mathematical logic that studies Set (mathematics), sets, which can be informally described as collections of objects. Although objects of any kind can be collected into a set, set theory – as a branch of mathema ...
. It also made Alfred Tarski's approach to model theory
In mathematical logic, model theory is the study of the relationship between theory (mathematical logic), formal theories (a collection of Sentence (mathematical logic), sentences in a formal language expressing statements about a Structure (mat ...
possible and provided the foundation of modern mathematical logic.
See also
References
Notes
Citations
Bibliography
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *External links
{{Authority control Formal sciences