Lane–Emden equation on:
[Wikipedia]
[Google]
[Amazon]
In astrophysics, the Lane–Emden equation is a dimensionless form of
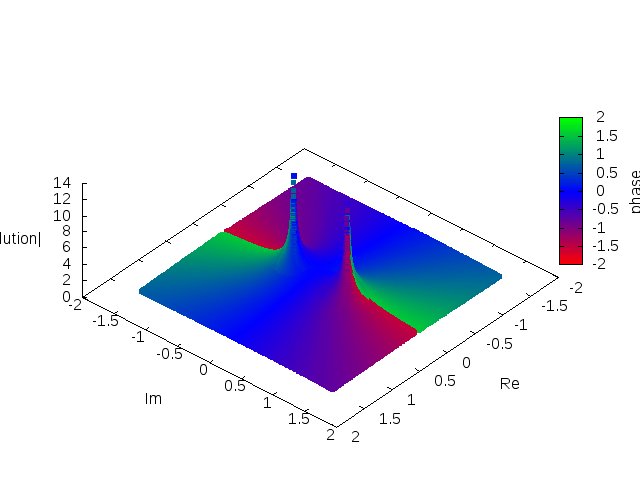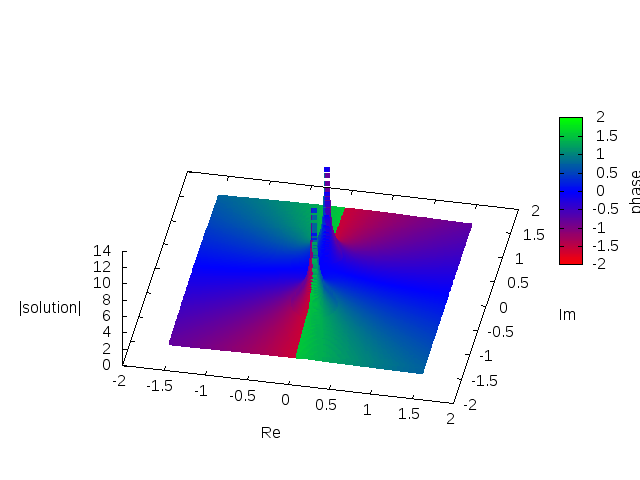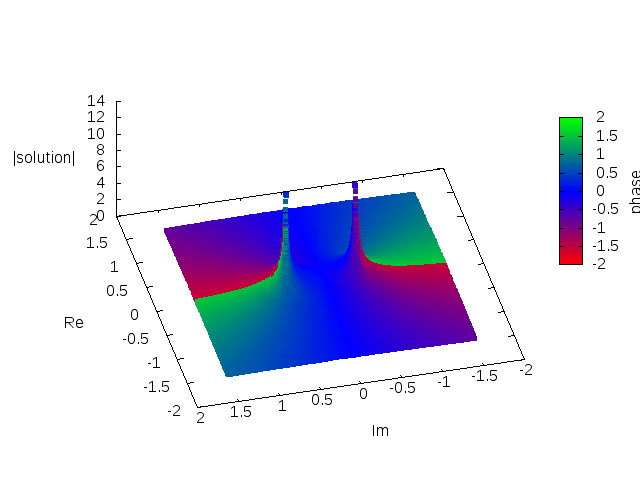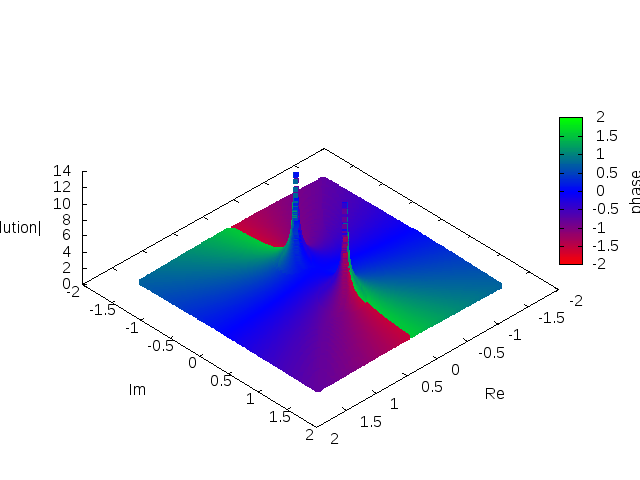 The
The
Poisson's equation
Poisson's equation is an elliptic partial differential equation of broad utility in theoretical physics. For example, the solution to Poisson's equation is the potential field caused by a given electric charge or mass density distribution; with t ...
for the gravitational potential of a Newtonian self-gravitating, spherically symmetric, polytropic fluid. It is named after astrophysicists Jonathan Homer Lane
Jonathan Homer Lane (August 9, 1819 – May 3, 1880) was an American astrophysicist and inventor.
Biography
Lane's parents were Mark and Henrietta (née Tenny) Lane and his education was at the Phillips Exeter Academy in Exeter, New Hampsh ...
and Robert Emden
Jacob Robert Emden (4 March 1862 – 8 October 1940) was a Swiss astrophysicist and meteorologist. He is best known for his book, ''Gaskugeln: Anwendungen der mechanischen Wärmetheorie auf kosmologische und meteorologische probleme'' (Gas sphe ...
. The equation reads
:
where is a dimensionless radius and is related to the density, and thus the pressure, by for central density . The index is the polytropic index that appears in the polytropic equation of state,
:
where and are the pressure and density, respectively, and is a constant of proportionality. The standard boundary conditions are and . Solutions thus describe the run of pressure and density with radius and are known as ''polytropes'' of index . If an isothermal fluid (polytropic index tends to infinity) is used instead of a polytropic fluid, one obtains the Emden–Chandrasekhar equation
In astrophysics, the Emden–Chandrasekhar equation is a dimensionless form of the Poisson equation for the density distribution of a spherically symmetric isothermal gas sphere subjected to its own gravitational force, named after Robert Emden a ...
.
Applications
Physically, hydrostatic equilibrium connects the gradient of the potential, the density, and the gradient of the pressure, whereas Poisson's equation connects the potential with the density. Thus, if we have a further equation that dictates how the pressure and density vary with respect to one another, we can reach a solution. The particular choice of a polytropic gas as given above makes the mathematical statement of the problem particularly succinct and leads to the Lane–Emden equation. The equation is a useful approximation for self-gravitating spheres of plasma such as stars, but typically it is a rather limiting assumption.Derivation
From hydrostatic equilibrium
Consider a self-gravitating, spherically symmetric fluid inhydrostatic equilibrium
In fluid mechanics, hydrostatic equilibrium (hydrostatic balance, hydrostasy) is the condition of a fluid or plastic solid at rest, which occurs when external forces, such as gravity, are balanced by a pressure-gradient force. In the planetary ...
. Mass is conserved and thus described by the continuity equation
:
where is a function of . The equation of hydrostatic equilibrium is
:
where is also a function of . Differentiating again gives
:
where the continuity equation has been used to replace the mass gradient. Multiplying both sides by and collecting the derivatives of on the left, one can write
:
Dividing both sides by yields, in some sense, a dimensional form of the desired equation. If, in addition, we substitute for the polytropic equation of state with and , we have
:
Gathering the constants and substituting , where
:
we have the Lane–Emden equation,
:
From Poisson's equation
Equivalently, one can start withPoisson's equation
Poisson's equation is an elliptic partial differential equation of broad utility in theoretical physics. For example, the solution to Poisson's equation is the potential field caused by a given electric charge or mass density distribution; with t ...
,
:
One can replace the gradient of the potential using the hydrostatic equilibrium, via
:
which again yields the dimensional form of the Lane–Emden equation.
Exact solutions
For a given value of the polytropic index , denote the solution to the Lane–Emden equation as . In general, the Lane–Emden equation must be solved numerically to find . There are exact, analytic solutions for certain values of , in particular: . For between 0 and 5, the solutions are continuous and finite in extent, with the radius of the star given by , where . For a given solution , the density profile is given by : . The total mass of the model star can be found by integrating the density over radius, from 0 to . The pressure can be found using the polytropic equation of state, , i.e. : Finally, if the gas isideal
Ideal may refer to:
Philosophy
* Ideal (ethics), values that one actively pursues as goals
* Platonic ideal, a philosophical idea of trueness of form, associated with Plato
Mathematics
* Ideal (ring theory), special subsets of a ring considere ...
, the equation of state is , where is the Boltzmann constant
The Boltzmann constant ( or ) is the proportionality factor that relates the average relative kinetic energy of particles in a gas with the thermodynamic temperature of the gas. It occurs in the definitions of the kelvin and the gas constant, ...
and the mean molecular weight. The temperature profile is then given by
:
In spherically symmetric cases, the Lane–Emden equation is integrable for only three values of the polytropic index .
For ''n'' = 0
If , the equation becomes : Re-arranging and integrating once gives : Dividing both sides by and integrating again gives : The boundary conditions and imply that the constants of integration are and . Therefore, :For ''n'' = 1
When , the equation can be expanded in the form : One assumes a power series solution: : This leads to a recursive relationship for the expansion coefficients: : This relation can be solved leading to the general solution: : The boundary condition for a physical polytrope demands that as . This requires that , thus leading to the solution: :For ''n'' = 5
We start from with the Lane–Emden equation: : Rewriting for produces: : Differentiating with respect to ''ξ'' leads to: : Reduced, we come by: : Therefore, the Lane–Emden equation has the solution : when . This solution is finite in mass but infinite in radial extent, and therefore the complete polytrope does not represent a physical solution. Chandrasekhar believed for a long time that finding other solution for "is complicated and involves elliptic integrals".Srivastava's solution
In 1962, Sambhunath Srivastava found an explicit solution when . His solution is given by : and from this solution, a family of solutions can be obtained using homology transformation. Since this solution does not satisfy the conditions at the origin (in fact, it is oscillatory with amplitudes growing indefinitely as the origin is approached), this solution can be used in composite stellar models.Analytic solutions
In applications, the main role play analytic solutions that are expressible by the convergentpower series
In mathematics, a power series (in one variable) is an infinite series of the form
\sum_^\infty a_n \left(x - c\right)^n = a_0 + a_1 (x - c) + a_2 (x - c)^2 + \dots
where ''an'' represents the coefficient of the ''n''th term and ''c'' is a con ...
expanded around some initial point. Typically the expansion point is , which is also a singular point (fixed singularity) of the equation, and there is provided some initial data at the centre of the star. One can prove that the equation has the convergent power series/analytic solution around the origin of the form
.
 The
The radius of convergence
In mathematics, the radius of convergence of a power series is the radius of the largest disk at the center of the series in which the series converges. It is either a non-negative real number or \infty. When it is positive, the power series ...
of this series is limited due to existence of two singularities on the imaginary axis in the complex plane. These singularities are located symmetrically with respect to the origin. Their position change when we change equation parameters and the initial condition , and therefore, they are called movable singularities due to classification of the singularities of non-linear ordinary differential equations in the complex plane by Paul Painlevé
Paul Painlevé (; 5 December 1863 – 29 October 1933) was a French mathematician and statesman. He served twice as Prime Minister of the Third Republic: 12 September – 13 November 1917 and 17 April – 22 November 1925. His entry into politic ...
. A similar structure of singularities appears in other non-linear equations that result from the reduction of the Laplace operator in spherical symmetry, e.g., Isothermal Sphere equation.
Analytic solutions can be extended along the real line by analytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of definition of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a n ...
procedure resulting in the full profile of the star or molecular cloud
A molecular cloud, sometimes called a stellar nursery (if star formation is occurring within), is a type of interstellar cloud, the density and size of which permit absorption nebulae, the formation of molecules (most commonly molecular hydroge ...
cores. Two analytic solutions with the overlapping circles of convergence can also be matched on the overlap to the larger domain solution, which is a commonly used method of construction of profiles of required properties.
The series solution is also used in the numerical integration of the equation. It is used to shift the initial data for analytic solution slightly away from the origin since at the origin the numerical methods fail due to the singularity of the equation.
Numerical solutions
In general, solutions are found by numerical integration. Many standard methods require that the problem is formulated as a system of first-orderordinary differential equation
In mathematics, an ordinary differential equation (ODE) is a differential equation whose unknown(s) consists of one (or more) function(s) of one variable and involves the derivatives of those functions. The term ''ordinary'' is used in contrast ...
s. For example,
:
Here, is interpreted as the dimensionless mass, defined by . The relevant initial conditions are and . The first equation represents hydrostatic equilibrium and the second represents mass conservation.
Homologous variables
Homology-invariant equation
It is known that if is a solution of the Lane–Emden equation, then so is . Solutions that are related in this way are called ''homologous''; the process that transforms them is ''homology''. If one chooses variables that are invariant to homology, then we can reduce the order of the Lane–Emden equation by one. A variety of such variables exist. A suitable choice is : and : We can differentiate the logarithms of these variables with respect to , which gives : and : . Finally, we can divide these two equations to eliminate the dependence on , which leaves : This is now a single first-order equation.Topology of the homology-invariant equation
The homology-invariant equation can be regarded as the autonomous pair of equations : and : The behaviour of solutions to these equations can be determined by linear stability analysis. The critical points of the equation (where ) and the eigenvalues and eigenvectors of the Jacobian matrix are tabulated below. :See also
*Emden–Chandrasekhar equation
In astrophysics, the Emden–Chandrasekhar equation is a dimensionless form of the Poisson equation for the density distribution of a spherically symmetric isothermal gas sphere subjected to its own gravitational force, named after Robert Emden a ...
* Chandrasekhar's white dwarf equation
References
Further reading
* *External links
* {{DEFAULTSORT:Lane-Emden equation Astrophysics Ordinary differential equations