|
Correlation Indicators
In statistics, correlation or dependence is any statistical relationship, whether causal or not, between two random variables or bivariate data. Although in the broadest sense, "correlation" may indicate any type of association, in statistics it usually refers to the degree to which a pair of variables are '' linearly'' related. Familiar examples of dependent phenomena include the correlation between the height of parents and their offspring, and the correlation between the price of a good and the quantity the consumers are willing to purchase, as it is depicted in the demand curve. Correlations are useful because they can indicate a predictive relationship that can be exploited in practice. For example, an electrical utility may produce less power on a mild day based on the correlation between electricity demand and weather. In this example, there is a causal relationship, because extreme weather causes people to use more electricity for heating or cooling. However, in gen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
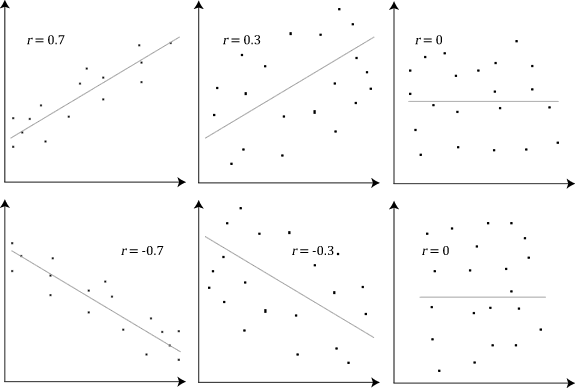
Correlation Examples2
In statistics, correlation or dependence is any statistical relationship, whether causality, causal or not, between two random variables or bivariate data. Although in the broadest sense, "correlation" may indicate any type of association, in statistics it usually refers to the degree to which a pair of variables are ''line (geometry), linearly'' related. Familiar examples of dependent phenomena include the correlation between the human height, height of parents and their offspring, and the correlation between the price of a good and the quantity the consumers are willing to purchase, as it is depicted in the demand curve. Correlations are useful because they can indicate a predictive relationship that can be exploited in practice. For example, an electrical utility may produce less power on a mild day based on the correlation between electricity demand and weather. In this example, there is a causality, causal relationship, because extreme weather causes people to use more ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pearson Correlation Coefficient And Associated Scatterplots
Pearson may refer to: Organizations Education * Lester B. Pearson College, Victoria, British Columbia, Canada * Pearson College (UK), London, owned by Pearson PLC * Lester B. Pearson High School (other) Companies * Pearson plc, a UK-based international media conglomerate, best known as a book publisher ** Pearson Education, the textbook division of Pearson PLC *** Pearson-Longman, an imprint of Pearson Education * Pearson Yachts Pearson Yachts was a sailboat manufacturer founded by Everett Pearson and Clinton Pearson in 1956. One of the first fiberglass sailboat manufacturers, they grew rapidly during the 60s and 70s, while also developing and designing new boats. Howe ... Places * Pearson, Georgia, a US city * Pearson, Texas, an unincorporated community in the US * Pearson, Victoria, a ghost town in Australia * Pearson, Wisconsin, an unincorporated community in the US * Toronto Pearson International Airport, in Toronto, Ontario, Canada * Pearson Field, in Vancouve ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Uncorrelated
In probability theory and statistics, two real-valued random variables, X, Y, are said to be uncorrelated if their covariance, \operatorname ,Y= \operatorname Y- \operatorname \operatorname /math>, is zero. If two variables are uncorrelated, there is no linear relationship between them. Uncorrelated random variables have a Pearson correlation coefficient, when it exists, of zero, except in the trivial case when either variable has zero variance (is a constant). In this case the correlation is undefined. In general, uncorrelatedness is not the same as orthogonality, except in the special case where at least one of the two random variables has an expected value of 0. In this case, the covariance is the expectation of the product, and X and Y are uncorrelated if and only if In logic and related fields such as mathematics and philosophy, "if and only if" (often shortened as "iff") is paraphrased by the biconditional, a logical connective between statements. The bicondit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Independence
Independence is a fundamental notion in probability theory, as in statistics and the theory of stochastic processes. Two events are independent, statistically independent, or stochastically independent if, informally speaking, the occurrence of one does not affect the probability of occurrence of the other or, equivalently, does not affect the odds. Similarly, two random variables are independent if the realization of one does not affect the probability distribution of the other. When dealing with collections of more than two events, two notions of independence need to be distinguished. The events are called pairwise independent if any two events in the collection are independent of each other, while mutual independence (or collective independence) of events means, informally speaking, that each event is independent of any combination of other events in the collection. A similar notion exists for collections of random variables. Mutual independence implies pairwise independence ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Dependence
In the theory of vector spaces, a set of vectors is said to be if there exists no nontrivial linear combination of the vectors that equals the zero vector. If such a linear combination exists, then the vectors are said to be . These concepts are central to the definition of dimension. A vector space can be of finite dimension or infinite dimension depending on the maximum number of linearly independent vectors. The definition of linear dependence and the ability to determine whether a subset of vectors in a vector space is linearly dependent are central to determining the dimension of a vector space. Definition A sequence of vectors \mathbf_1, \mathbf_2, \dots, \mathbf_k from a vector space is said to be ''linearly dependent'', if there exist scalars a_1, a_2, \dots, a_k, not all zero, such that :a_1\mathbf_1 + a_2\mathbf_2 + \cdots + a_k\mathbf_k = \mathbf, where \mathbf denotes the zero vector. This implies that at least one of the scalars is nonzero, say a_1\ne ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Open Interval
In mathematics, a real interval is the set (mathematics), set of all real numbers lying between two fixed endpoints with no "gaps". Each endpoint is either a real number or positive or negative infinity, indicating the interval extends without a Bounded set, bound. A real interval can contain neither endpoint, either endpoint, or both endpoints, excluding any endpoint which is infinite. For example, the set of real numbers consisting of , , and all numbers in between is an interval, denoted and called the unit interval; the set of all positive real numbers is an interval, denoted ; the set of all real numbers is an interval, denoted ; and any single real number is an interval, denoted . Intervals are ubiquitous in mathematical analysis. For example, they occur implicitly in the epsilon-delta definition of continuity; the intermediate value theorem asserts that the image of an interval by a continuous function is an interval; integrals of real functions are defined over an int ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Absolute Value
In mathematics, the absolute value or modulus of a real number x, is the non-negative value without regard to its sign. Namely, , x, =x if x is a positive number, and , x, =-x if x is negative (in which case negating x makes -x positive), and For example, the absolute value of 3 and the absolute value of −3 is The absolute value of a number may be thought of as its distance from zero. Generalisations of the absolute value for real numbers occur in a wide variety of mathematical settings. For example, an absolute value is also defined for the complex numbers, the quaternions, ordered rings, fields and vector spaces. The absolute value is closely related to the notions of magnitude, distance, and norm in various mathematical and physical contexts. Terminology and notation In 1806, Jean-Robert Argand introduced the term ''module'', meaning ''unit of measure'' in French, specifically for the ''complex'' absolute value,Oxford English Dictionary, Draft Revision, Ju ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
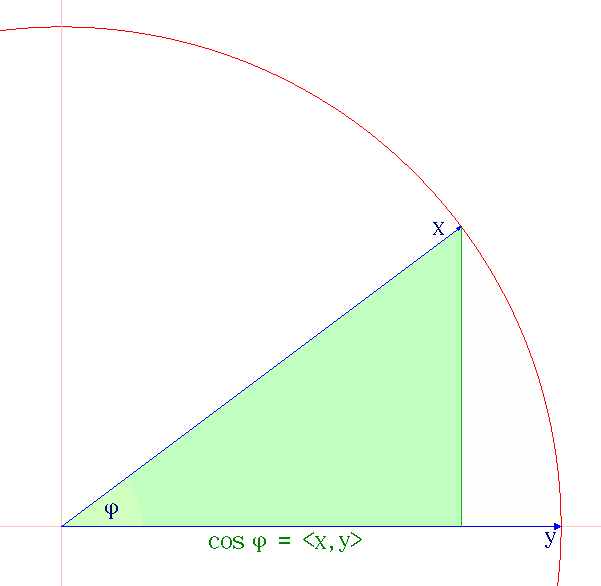
Cauchy–Schwarz Inequality
The Cauchy–Schwarz inequality (also called Cauchy–Bunyakovsky–Schwarz inequality) is an upper bound on the absolute value of the inner product between two vectors in an inner product space in terms of the product of the vector norms. It is considered one of the most important and widely used inequalities in mathematics. Inner products of vectors can describe finite sums (via finite-dimensional vector spaces), infinite series (via vectors in sequence spaces), and integrals (via vectors in Hilbert spaces). The inequality for sums was published by . The corresponding inequality for integrals was published by and . Schwarz gave the modern proof of the integral version. Statement of the inequality The Cauchy–Schwarz inequality states that for all vectors \mathbf and \mathbf of an inner product space where \langle \cdot, \cdot \rangle is the inner product. Examples of inner products include the real and complex dot product; see the examples in inner product. Every ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Moment (mathematics)
In mathematics, the moments of a function are certain quantitative measures related to the shape of the function's graph. If the function represents mass density, then the zeroth moment is the total mass, the first moment (normalized by total mass) is the center of mass, and the second moment is the moment of inertia. If the function is a probability distribution, then the first moment is the expected value, the second central moment is the variance, the third standardized moment is the skewness, and the fourth standardized moment is the kurtosis. For a distribution of mass or probability on a bounded interval, the collection of all the moments (of all orders, from to ) uniquely determines the distribution ( Hausdorff moment problem). The same is not true on unbounded intervals ( Hamburger moment problem). In the mid-nineteenth century, Pafnuty Chebyshev became the first person to think systematically in terms of the moments of random variables. Significance of th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Expected Value
In probability theory, the expected value (also called expectation, expectancy, expectation operator, mathematical expectation, mean, expectation value, or first Moment (mathematics), moment) is a generalization of the weighted average. Informally, the expected value is the arithmetic mean, mean of the possible values a random variable can take, weighted by the probability of those outcomes. Since it is obtained through arithmetic, the expected value sometimes may not even be included in the sample data set; it is not the value you would expect to get in reality. The expected value of a random variable with a finite number of outcomes is a weighted average of all possible outcomes. In the case of a continuum of possible outcomes, the expectation is defined by Integral, integration. In the axiomatic foundation for probability provided by measure theory, the expectation is given by Lebesgue integration. The expected value of a random variable is often denoted by , , or , with a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Random Variables
A random variable (also called random quantity, aleatory variable, or stochastic variable) is a mathematical formalization of a quantity or object which depends on random events. The term 'random variable' in its mathematical definition refers to neither randomness nor variability but instead is a mathematical function in which * the domain is the set of possible outcomes in a sample space (e.g. the set \ which are the possible upper sides of a flipped coin heads H or tails T as the result from tossing a coin); and * the range is a measurable space (e.g. corresponding to the domain above, the range might be the set \ if say heads H mapped to -1 and T mapped to 1). Typically, the range of a random variable is a subset of the real numbers. Informally, randomness typically represents some fundamental element of chance, such as in the roll of a die; it may also represent uncertainty, such as measurement error. However, the interpretation of probability is philosophic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Francis Galton
Sir Francis Galton (; 16 February 1822 – 17 January 1911) was an English polymath and the originator of eugenics during the Victorian era; his ideas later became the basis of behavioural genetics. Galton produced over 340 papers and books. He also developed the statistical concept of correlation and widely promoted regression toward the mean. He was the first to apply statistical methods to the study of human differences and inheritance of intelligence, and introduced the use of questionnaires and Statistical survey, surveys for collecting data on human communities, which he needed for genealogical and biographical works and for his anthropometrics, anthropometric studies. He popularised the phrase "nature versus nurture". His book ''Hereditary Genius'' (1869) was the first social scientific attempt to study genius and greatness. As an investigator of the human mind, he founded psychometrics and differential psychology, as well as the lexical hypothesis of personality. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |