connectivity (graph theory) on:
[Wikipedia]
[Google]
[Amazon]

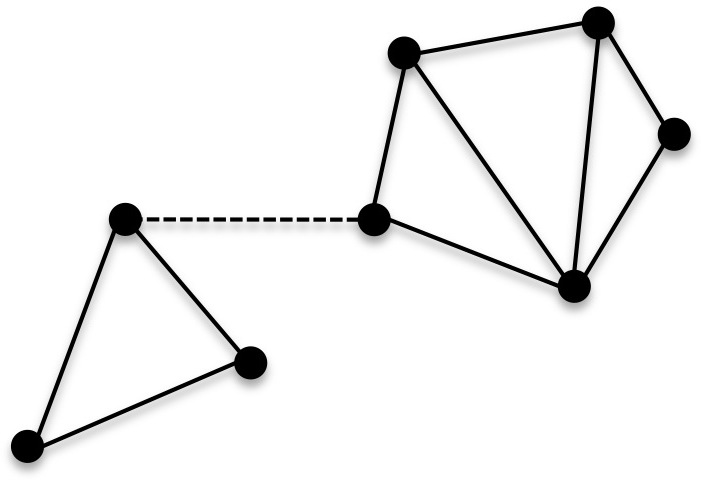 In
In
 In an
In an

 In
In mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ...
and computer science
Computer science is the study of computation, information, and automation. Computer science spans Theoretical computer science, theoretical disciplines (such as algorithms, theory of computation, and information theory) to Applied science, ...
, connectivity is one of the basic concepts of graph theory
In mathematics and computer science, graph theory is the study of ''graph (discrete mathematics), graphs'', which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of ''Vertex (graph ...
: it asks for the minimum
In mathematical analysis, the maximum and minimum of a function are, respectively, the greatest and least value taken by the function. Known generically as extremum, they may be defined either within a given range (the ''local'' or ''relative ...
number of elements (nodes or edges) that need to be removed to separate the remaining nodes into two or more isolated subgraphs. It is closely related to the theory of network flow problems. The connectivity of a graph is an important measure of its resilience as a network.
Connected vertices and graphs
undirected graph
In discrete mathematics, particularly in graph theory, a graph is a structure consisting of a set of objects where some pairs of the objects are in some sense "related". The objects are represented by abstractions called '' vertices'' (also call ...
, two vertices and are called connected if contains a path
A path is a route for physical travel – see Trail.
Path or PATH may also refer to:
Physical paths of different types
* Bicycle path
* Bridle path, used by people on horseback
* Course (navigation), the intended path of a vehicle
* Desir ...
from to . Otherwise, they are called disconnected. If the two vertices are additionally connected by a path of length (that is, they are the endpoints of a single edge), the vertices are called adjacent.
A graph
Graph may refer to:
Mathematics
*Graph (discrete mathematics), a structure made of vertices and edges
**Graph theory, the study of such graphs and their properties
*Graph (topology), a topological space resembling a graph in the sense of discret ...
is said to be connected if every pair of vertices in the graph is connected. This means that there is a path
A path is a route for physical travel – see Trail.
Path or PATH may also refer to:
Physical paths of different types
* Bicycle path
* Bridle path, used by people on horseback
* Course (navigation), the intended path of a vehicle
* Desir ...
between every pair of vertices. An undirected graph that is not connected is called disconnected. An undirected graph is therefore disconnected if there exist two vertices in such that no path in has these vertices as endpoints. A graph with just one vertex is connected. An edgeless graph with two or more vertices is disconnected.
A directed graph is called weakly connected if replacing all of its directed edges with undirected edges produces a connected (undirected) graph. It is unilaterally connected or unilateral (also called semiconnected) if it contains a directed path from to or a directed path from to for every pair of vertices . It is strongly connected, or simply strong, if it contains a directed path from to and a directed path from to for every pair of vertices .
Components and cuts
A connected component is a maximal connected subgraph of an undirected graph. Each vertex belongs to exactly one connected component, as does each edge. A graph is connectedif and only if
In logic and related fields such as mathematics and philosophy, "if and only if" (often shortened as "iff") is paraphrased by the biconditional, a logical connective between statements. The biconditional is true in two cases, where either bo ...
it has exactly one connected component.
The strong components are the maximal strongly connected subgraphs of a directed graph.
A vertex cut or separating set of a connected graph is a set of vertices whose removal renders disconnected. The vertex connectivity (where is not a complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge. A complete digraph is a directed graph in which every pair of distinct vertices i ...
) is the size of a smallest vertex cut. A graph is called '-vertex-connected or '-connected if its vertex connectivity is or greater.
More precisely, any graph (complete or not) is said to be ''-vertex-connected'' if it contains at least vertices, but does not contain a set of vertices whose removal disconnects the graph; and is defined as the largest such that is -connected. In particular, a complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge. A complete digraph is a directed graph in which every pair of distinct vertices i ...
with vertices, denoted , has no vertex cuts at all, but .
A vertex cut for two vertices and is a set of vertices whose removal from the graph disconnects and . The local connectivity is the size of a smallest vertex cut separating and . Local connectivity is symmetric for undirected graphs; that is, . Moreover, except for complete graphs, equals the minimum of over all nonadjacent pairs of vertices .
-connectivity is also called '' biconnectivity'' and -connectivity is also called ''triconnectivity''. A graph which is connected but not -connected is sometimes called ''separable''.
Analogous concepts can be defined for edges. In the simple case in which cutting a single, specific edge would disconnect the graph, that edge is called a ''bridge
A bridge is a structure built to Span (engineering), span a physical obstacle (such as a body of water, valley, road, or railway) without blocking the path underneath. It is constructed for the purpose of providing passage over the obstacle, whi ...
''. More generally, an edge cut of is a set of edges whose removal renders the graph disconnected. The ''edge-connectivity
In graph theory, a connected Graph (discrete mathematics), graph is -edge-connected if it remains Connectivity (graph theory), connected whenever fewer than edges are removed.
The edge-connectivity of a graph is the largest for which the graph ...
'' is the size of a smallest edge cut, and the local edge-connectivity of two vertices is the size of a smallest edge cut disconnecting from . Again, local edge-connectivity is symmetric. A graph is called ''-edge-connected'' if its edge connectivity is or greater.
A graph is said to be ''maximally connected'' if its connectivity equals its minimum degree. A graph is said to be ''maximally edge-connected'' if its edge-connectivity equals its minimum degree.
Super- and hyper-connectivity
A graph is said to be ''super-connected'' or ''super-κ'' if every minimum vertex cut isolates a vertex. A graph is said to be ''hyper-connected'' or ''hyper-κ'' if the deletion of each minimum vertex cut creates exactly two components, one of which is an isolated vertex. A graph is ''semi-hyper-connected'' or ''semi-hyper-κ'' if any minimum vertex cut separates the graph into exactly two components. More precisely: a connected graph is said to be ''super-connected'' or ''super-κ'' if all minimum vertex-cuts consist of the vertices adjacent with one (minimum-degree) vertex. A connected graph is said to be ''super-edge-connected'' or ''super-λ'' if all minimum edge-cuts consist of the edges incident on some (minimum-degree) vertex. A cutset of is called a non-trivial cutset if does not contain the neighborhood of any vertex . Then the ''superconnectivity'' of is A non-trivial edge-cut and the ''edge-superconnectivity'' are defined analogously.Menger's theorem
One of the most important facts about connectivity in graphs is Menger's theorem, which characterizes the connectivity and edge-connectivity of a graph in terms of the number of independent paths between vertices. If and are vertices of a graph , then a collection of paths between and is called independent if no two of them share a vertex (other than and themselves). Similarly, the collection is edge-independent if no two paths in it share an edge. The number of mutually independent paths between and is written as , and the number of mutually edge-independent paths between and is written as . Menger's theorem asserts that for distinct vertices ''u'',''v'', equals , and if ''u'' is also not adjacent to ''v'' then equals . This fact is actually a special case of the max-flow min-cut theorem.Computational aspects
The problem of determining whether two vertices in a graph are connected can be solved efficiently using asearch algorithm
In computer science, a search algorithm is an algorithm designed to solve a search problem. Search algorithms work to retrieve information stored within particular data structure, or calculated in the Feasible region, search space of a problem do ...
, such as breadth-first search
Breadth-first search (BFS) is an algorithm for searching a tree data structure for a node that satisfies a given property. It starts at the tree root and explores all nodes at the present depth prior to moving on to the nodes at the next dept ...
. More generally, it is easy to determine computationally whether a graph is connected (for example, by using a disjoint-set data structure
In computer science, a disjoint-set data structure, also called a union–find data structure or merge–find set, is a data structure that stores a collection of Disjoint sets, disjoint (non-overlapping) Set (mathematics), sets. Equivalently, it ...
), or to count the number of connected components. A simple algorithm might be written in pseudo-code as follows:
#Begin at any arbitrary node of the graph .
#Proceed from that node using either depth-first or breadth-first search, counting all nodes reached.
#Once the graph has been entirely traversed, if the number of nodes counted is equal to the number of nodes of , the graph is connected; otherwise it is disconnected.
By Menger's theorem, for any two vertices and in a connected graph , the numbers and can be determined efficiently using the max-flow min-cut algorithm. The connectivity and edge-connectivity of can then be computed as the minimum values of and , respectively.
In computational complexity theory
In theoretical computer science and mathematics, computational complexity theory focuses on classifying computational problems according to their resource usage, and explores the relationships between these classifications. A computational problem ...
, SL is the class of problems log-space reducible to the problem of determining whether two vertices in a graph are connected, which was proved to be equal to L by Omer Reingold in 2004. Hence, undirected graph connectivity may be solved in space.
The problem of computing the probability that a Bernoulli random graph is connected is called network reliability and the problem of computing whether two given vertices are connected the ST-reliability problem. Both of these are #P-hard.
Number of connected graphs
The number of distinct connected labeled graphs with ''n'' nodes is tabulated in theOn-Line Encyclopedia of Integer Sequences
The On-Line Encyclopedia of Integer Sequences (OEIS) is an online database of integer sequences. It was created and maintained by Neil Sloane while researching at AT&T Labs. He transferred the intellectual property and hosting of the OEIS to th ...
as sequence . The first few non-trivial terms are

Examples
* The vertex- and edge-connectivities of a disconnected graph are both . * -connectedness is equivalent to connectedness for graphs of at least two vertices. * Thecomplete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge. A complete digraph is a directed graph in which every pair of distinct vertices i ...
on vertices has edge-connectivity equal to . Every other simple graph
In discrete mathematics, particularly in graph theory, a graph is a structure consisting of a Set (mathematics), set of objects where some pairs of the objects are in some sense "related". The objects are represented by abstractions called ''Ver ...
on vertices has strictly smaller edge-connectivity.
* In a tree
In botany, a tree is a perennial plant with an elongated stem, or trunk, usually supporting branches and leaves. In some usages, the definition of a tree may be narrower, e.g., including only woody plants with secondary growth, only ...
, the local edge-connectivity between any two distinct vertices is .
Bounds on connectivity
* The vertex-connectivity of a graph is less than or equal to its edge-connectivity. That is, . * The edge-connectivity for a graph with at least 2 vertices is less than or equal to the minimum degree of the graph because removing all the edges that are incident to a vertex of minimum degree will disconnect that vertex from the rest of the graph. * For avertex-transitive graph
In the mathematics, mathematical field of graph theory, an Graph automorphism, automorphism is a permutation of the Vertex (graph theory), vertices such that edges are mapped to edges and non-edges are mapped to non-edges. A graph is a vertex-tr ...
of degree , we have: .
* For a vertex-transitive graph of degree , or for any (undirected) minimal Cayley graph
In mathematics, a Cayley graph, also known as a Cayley color graph, Cayley diagram, group diagram, or color group, is a Graph (discrete mathematics), graph that encodes the abstract structure of a group (mathematics), group. Its definition is sug ...
of degree , or for any symmetric graph of degree , both kinds of connectivity are equal: .
Other properties
* Connectedness is preserved by graph homomorphisms. * If is connected then itsline graph
In the mathematics, mathematical discipline of graph theory, the line graph of an undirected graph is another graph that represents the adjacencies between edge (graph theory), edges of . is constructed in the following way: for each edge i ...
is also connected.
* A graph is -edge-connected if and only if it has an orientation that is strongly connected.
* Balinski's theorem states that the polytopal graph (-skeleton
A skeleton is the structural frame that supports the body of most animals. There are several types of skeletons, including the exoskeleton, which is a rigid outer shell that holds up an organism's shape; the endoskeleton, a rigid internal fra ...
) of a -dimensional convex polytope
A convex polytope is a special case of a polytope, having the additional property that it is also a convex set contained in the n-dimensional Euclidean space \mathbb^n. Most texts. use the term "polytope" for a bounded convex polytope, and the wo ...
is a -vertex-connected graph. Steinitz's previous theorem that any 3-vertex-connected planar graph
In graph theory, a planar graph is a graph (discrete mathematics), graph that can be graph embedding, embedded in the plane (geometry), plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints. ...
is a polytopal graph (Steinitz's theorem
In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedron, convex polyhedra: they are exactly the vertex connect ...
) gives a partial converse.
* According to a theorem of G. A. Dirac, if a graph is -connected for , then for every set of vertices in the graph there is a cycle that passes through all the vertices in the set.. The converse is true when .
See also
* Algebraic connectivity * Cheeger constant (graph theory) * Dynamic connectivity,Disjoint-set data structure
In computer science, a disjoint-set data structure, also called a union–find data structure or merge–find set, is a data structure that stores a collection of Disjoint sets, disjoint (non-overlapping) Set (mathematics), sets. Equivalently, it ...
* Expander graph
In graph theory, an expander graph is a sparse graph that has strong connectivity properties, quantified using vertex, edge or spectral expansion. Expander constructions have spawned research in pure and applied mathematics, with several appli ...
* Strength of a graph
References
{{reflist