Zeno's paradoxes on:
[Wikipedia]
[Google]
[Amazon]
Zeno's paradoxes are a series of philosophical
"Physics" by Aristotle translated by R. P. Hardie and R. K. Gaye and Simplicius's commentary thereon) are essentially equivalent to one another. Aristotle offered a response to some of them. Popular literature often misrepresents Zeno's arguments. For example, Zeno is often said to have argued that the sum of an infinite number of terms must itself be infinite–with the result that not only the time, but also the distance to be travelled, become infinite. However, none of the original ancient sources has Zeno discussing the sum of any infinite series. Simplicius has Zeno saying "it is impossible to traverse an infinite number of things in a finite time". This presents Zeno's problem not with finding the ''sum'', but rather with ''finishing'' a task with an infinite number of steps: how can one ever get from A to B, if an infinite number of (non-instantaneous) events can be identified that need to precede the arrival at B, and one cannot reach even the beginning of a "last event"?
 Suppose
Suppose
ImageSize= width:800 height:100
PlotArea= width:720 height:55 left:65 bottom:20
AlignBars= justify
Period= from:0 till:100
TimeAxis= orientation:horizontal
ScaleMajor= unit:year increment:10 start:0
ScaleMinor= unit:year increment:1 start:0
Colors=
id:homer value:rgb(0.4,0.8,1) # light purple
PlotData=
bar:homer fontsize:L color:homer
from:0 till:100
at:50 mark:(line,red)
at:25 mark:(line,black)
at:12.5 mark:(line,black)
at:6.25 mark:(line,black)
at:3.125 mark:(line,black)
at:1.5625 mark:(line,black)
at:0.78125 mark:(line,black)
at:0.390625 mark:(line,black)
at:0.1953125 mark:(line,black)
at:0.09765625 mark:(line,black)
The resulting sequence can be represented as:
:
This description requires one to complete an infinite number of tasks, which Zeno maintains is an impossibility.
This sequence also presents a second problem in that it contains no first distance to run, for any possible ( finite) first distance could be divided in half, and hence would not be first after all. Hence, the trip cannot even begin. The paradoxical conclusion then would be that travel over any finite distance can be neither completed nor begun, and so all motion must be an
 In the paradox of Achilles and the tortoise,
In the paradox of Achilles and the tortoise,
 In the arrow paradox, Zeno states that for motion to occur, an object must change the position which it occupies. He gives an example of an arrow in flight. He states that at any one (durationless) instant of time, the arrow is neither moving to where it is, nor to where it is not.
It cannot move to where it is not, because no time elapses for it to move there; it cannot move to where it is, because it is already there. In other words, at every instant of time there is no motion occurring. If everything is motionless at every instant, and time is entirely composed of instants, then motion is impossible.
Whereas the first two paradoxes divide space, this paradox starts by dividing time—and not into segments, but into points.
In the arrow paradox, Zeno states that for motion to occur, an object must change the position which it occupies. He gives an example of an arrow in flight. He states that at any one (durationless) instant of time, the arrow is neither moving to where it is, nor to where it is not.
It cannot move to where it is not, because no time elapses for it to move there; it cannot move to where it is, because it is already there. In other words, at every instant of time there is no motion occurring. If everything is motionless at every instant, and time is entirely composed of instants, then motion is impossible.
Whereas the first two paradoxes divide space, this paradox starts by dividing time—and not into segments, but into points.
 From Aristotle:
An expanded account of Zeno's arguments, as presented by Aristotle, is given in Simplicius's commentary ''On Aristotle's Physics''.
According to Angie Hobbs of The University of Sheffield, this paradox is intended to be considered together with the paradox of Achilles and the Tortoise, problematizing the concept of discrete space & time where the other problematizes the concept of infinitely divisible space & time.
From Aristotle:
An expanded account of Zeno's arguments, as presented by Aristotle, is given in Simplicius's commentary ''On Aristotle's Physics''.
According to Angie Hobbs of The University of Sheffield, this paradox is intended to be considered together with the paradox of Achilles and the Tortoise, problematizing the concept of discrete space & time where the other problematizes the concept of infinitely divisible space & time.
, Josh McHugh,
 Roughly contemporaneously during the
Roughly contemporaneously during the
Zeno’s Paradoxes
" Entry in the
Introduction to Mathematical Philosophy
Ludwig-Maximilians-Universität München * Silagadze, Z. K.
Zeno meets modern science
" *
Zeno's Paradox: Achilles and the Tortoise
' by Jon McLoone,
Kevin Brown on Zeno and the Paradox of Motion
* * * {{authority control Eponymous paradoxes Philosophical paradoxes Supertasks Mathematical paradoxes Paradoxes of infinity Physical paradoxes
arguments
An argument is a series of sentences, statements, or propositions some of which are called premises and one is the conclusion. The purpose of an argument is to give reasons for one's conclusion via justification, explanation, and/or persua ...
presented by the ancient Greek
Ancient Greek (, ; ) includes the forms of the Greek language used in ancient Greece and the classical antiquity, ancient world from around 1500 BC to 300 BC. It is often roughly divided into the following periods: Mycenaean Greek (), Greek ...
philosopher Zeno of Elea
Zeno of Elea (; ; ) was a pre-Socratic Greek philosopher from Elea, in Southern Italy (Magna Graecia). He was a student of Parmenides and one of the Eleatics. Zeno defended his instructor's belief in monism, the idea that only one single en ...
(c. 490–430 BC), primarily known through the works of Plato
Plato ( ; Greek language, Greek: , ; born BC, died 348/347 BC) was an ancient Greek philosopher of the Classical Greece, Classical period who is considered a foundational thinker in Western philosophy and an innovator of the writte ...
, Aristotle
Aristotle (; 384–322 BC) was an Ancient Greek philosophy, Ancient Greek philosopher and polymath. His writings cover a broad range of subjects spanning the natural sciences, philosophy, linguistics, economics, politics, psychology, a ...
, and later commentators like Simplicius of Cilicia. Zeno devised these paradoxes to support his teacher Parmenides
Parmenides of Elea (; ; fl. late sixth or early fifth century BC) was a Pre-Socratic philosophy, pre-Socratic ancient Greece, Greek philosopher from Velia, Elea in Magna Graecia (Southern Italy).
Parmenides was born in the Greek colony of Veli ...
's philosophy of monism
Monism attributes oneness or singleness () to a concept, such as to existence. Various kinds of monism can be distinguished:
* Priority monism states that all existing things go back to a source that is distinct from them; e.g., in Neoplatonis ...
, which posits that despite people's sensory experiences, reality is singular and unchanging. The paradoxes famously challenge the notions of plurality (the existence
Existence is the state of having being or reality in contrast to nonexistence and nonbeing. Existence is often contrasted with essence: the essence of an entity is its essential features or qualities, which can be understood even if one does ...
of many things), motion, space, and time by suggesting they lead to logical contradictions.
Zeno's work, primarily known from second-hand accounts since his original texts are lost, comprises forty "paradoxes of plurality," which argue against the coherence of believing in multiple existences, and several arguments against motion and change. Of these, only a few are definitively known today, including the renowned "Achilles Paradox", which illustrates the problematic concept of infinite divisibility in space
Space is a three-dimensional continuum containing positions and directions. In classical physics, physical space is often conceived in three linear dimensions. Modern physicists usually consider it, with time, to be part of a boundless ...
and time
Time is the continuous progression of existence that occurs in an apparently irreversible process, irreversible succession from the past, through the present, and into the future. It is a component quantity of various measurements used to sequ ...
. In this paradox, Zeno argues that a swift runner like Achilles
In Greek mythology, Achilles ( ) or Achilleus () was a hero of the Trojan War who was known as being the greatest of all the Greek warriors. The central character in Homer's ''Iliad'', he was the son of the Nereids, Nereid Thetis and Peleus, ...
cannot overtake a slower moving tortoise
Tortoises ( ) are reptiles of the family Testudinidae of the order Testudines (Latin for "tortoise"). Like other turtles, tortoises have a shell to protect from predation and other threats. The shell in tortoises is generally hard, and like o ...
with a head start, because the distance
Distance is a numerical or occasionally qualitative measurement of how far apart objects, points, people, or ideas are. In physics or everyday usage, distance may refer to a physical length or an estimation based on other criteria (e.g. "two co ...
between them can be infinitely subdivided, implying Achilles would require an infinite number of steps to catch the tortoise.
These paradoxes have stirred extensive philosophical and mathematical discussion throughout history
History is the systematic study of the past, focusing primarily on the Human history, human past. As an academic discipline, it analyses and interprets evidence to construct narratives about what happened and explain why it happened. Some t ...
, particularly regarding the nature of infinity and the continuity of space and time. Initially, Aristotle
Aristotle (; 384–322 BC) was an Ancient Greek philosophy, Ancient Greek philosopher and polymath. His writings cover a broad range of subjects spanning the natural sciences, philosophy, linguistics, economics, politics, psychology, a ...
's interpretation, suggesting a potential rather than actual infinity, was widely accepted. However, modern solutions leveraging the mathematical framework of calculus
Calculus is the mathematics, mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizations of arithmetic operations.
Originally called infinitesimal calculus or "the ...
have provided a different perspective, highlighting Zeno's significant early insight into the complexities of infinity and continuous motion. Zeno's paradoxes remain a pivotal reference point in the philosophical and mathematical exploration of reality, motion, and the infinite, influencing both ancient thought and modern scientific understanding.
History
The origins of the paradoxes are somewhat unclear, but they are generally thought to have been developed to supportParmenides
Parmenides of Elea (; ; fl. late sixth or early fifth century BC) was a Pre-Socratic philosophy, pre-Socratic ancient Greece, Greek philosopher from Velia, Elea in Magna Graecia (Southern Italy).
Parmenides was born in the Greek colony of Veli ...
' doctrine of monism
Monism attributes oneness or singleness () to a concept, such as to existence. Various kinds of monism can be distinguished:
* Priority monism states that all existing things go back to a source that is distinct from them; e.g., in Neoplatonis ...
, that all of reality is one, and that ''all change is impossible'', that is, that nothing ever changes in location or in any other respect. Diogenes Laërtius
Diogenes Laërtius ( ; , ; ) was a biographer of the Greek philosophers. Little is definitively known about his life, but his surviving book ''Lives and Opinions of Eminent Philosophers'' is a principal source for the history of ancient Greek ph ...
, citing Favorinus
Favorinus (c. 80 – c. 160 AD) was a Roman sophist and skeptic philosopher who flourished during the reign of Hadrian and the Second Sophistic.
Early life
He was of Gaulish ancestry, born in Arelate (Arles). He received a refined educa ...
, says that Zeno's teacher Parmenides was the first to introduce the paradox of Achilles and the tortoise. But in a later passage, Laërtius attributes the origin of the paradox to Zeno, explaining that Favorinus disagrees. Modern academics attribute the paradox to Zeno.
Many of these paradoxes argue that contrary to the evidence of one's senses, motion
In physics, motion is when an object changes its position with respect to a reference point in a given time. Motion is mathematically described in terms of displacement, distance, velocity, acceleration, speed, and frame of reference to an o ...
is nothing but an illusion
An illusion is a distortion of the senses, which can reveal how the mind normally organizes and interprets sensory stimulation. Although illusions distort the human perception of reality, they are generally shared by most people.
Illusions may ...
. In Plato's ''Parmenides'' (128a–d), Zeno is characterized as taking on the project of creating these paradoxes
A paradox is a logically self-contradictory statement or a statement that runs contrary to one's expectation. It is a statement that, despite apparently valid reasoning from true or apparently true premises, leads to a seemingly self-contradictor ...
because other philosophers claimed paradoxes arise when considering Parmenides' view. Zeno's arguments may then be early examples of a method of proof called ''reductio ad absurdum
In logic, (Latin for "reduction to absurdity"), also known as (Latin for "argument to absurdity") or ''apagogical argument'', is the form of argument that attempts to establish a claim by showing that the opposite scenario would lead to absur ...
'', also known as proof by contradiction
In logic, proof by contradiction is a form of proof that establishes the truth or the validity of a proposition by showing that assuming the proposition to be false leads to a contradiction.
Although it is quite freely used in mathematical pr ...
. Thus Plato has Zeno say the purpose of the paradoxes "is to show that their hypothesis that existences are many, if properly followed up, leads to still more absurd results than the hypothesis that they are one." Plato has Socrates
Socrates (; ; – 399 BC) was a Ancient Greek philosophy, Greek philosopher from Classical Athens, Athens who is credited as the founder of Western philosophy and as among the first moral philosophers of the Ethics, ethical tradition ...
claim that Zeno and Parmenides were essentially arguing exactly the same point. They are also credited as a source of the dialectic
Dialectic (; ), also known as the dialectical method, refers originally to dialogue between people holding different points of view about a subject but wishing to arrive at the truth through reasoned argument. Dialectic resembles debate, but the ...
method used by Socrates.
Paradoxes
Some of Zeno's nine surviving paradoxes (preserved in Aristotle's ''Physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge whi ...
''Aristotle's ''Physics''"Physics" by Aristotle translated by R. P. Hardie and R. K. Gaye and Simplicius's commentary thereon) are essentially equivalent to one another. Aristotle offered a response to some of them. Popular literature often misrepresents Zeno's arguments. For example, Zeno is often said to have argued that the sum of an infinite number of terms must itself be infinite–with the result that not only the time, but also the distance to be travelled, become infinite. However, none of the original ancient sources has Zeno discussing the sum of any infinite series. Simplicius has Zeno saying "it is impossible to traverse an infinite number of things in a finite time". This presents Zeno's problem not with finding the ''sum'', but rather with ''finishing'' a task with an infinite number of steps: how can one ever get from A to B, if an infinite number of (non-instantaneous) events can be identified that need to precede the arrival at B, and one cannot reach even the beginning of a "last event"?
Paradoxes of motion
Three of the strongest and most famous—that of Achilles and the tortoise, theDichotomy
A dichotomy () is a partition of a set, partition of a whole (or a set) into two parts (subsets). In other words, this couple of parts must be
* jointly exhaustive: everything must belong to one part or the other, and
* mutually exclusive: nothi ...
argument, and that of an arrow in flight—are presented in detail below.Dichotomy paradox
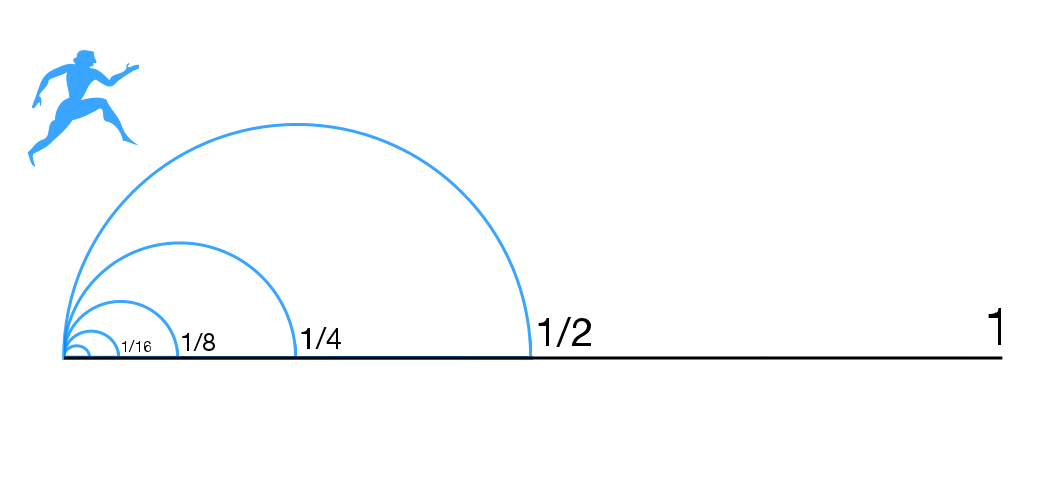
 Suppose
Suppose Atalanta
Atalanta (; ) is a heroine in Greek mythology.
There are two versions of the huntress Atalanta: one from Arcadia (region), Arcadia, whose parents were Iasus and Clymene (mythology), Clymene and who is primarily known from the tales of the Caly ...
wishes to walk to the end of a path. Before she can get there, she must get halfway there. Before she can get halfway there, she must get a quarter of the way there. Before traveling a quarter, she must travel one-eighth; before an eighth, one-sixteenth; and so on.
illusion
An illusion is a distortion of the senses, which can reveal how the mind normally organizes and interprets sensory stimulation. Although illusions distort the human perception of reality, they are generally shared by most people.
Illusions may ...
.
This argument is called the "Dichotomy
A dichotomy () is a partition of a set, partition of a whole (or a set) into two parts (subsets). In other words, this couple of parts must be
* jointly exhaustive: everything must belong to one part or the other, and
* mutually exclusive: nothi ...
" because it involves repeatedly splitting a distance into two parts. An example with the original sense can be found in an asymptote. It is also known as the Race Course paradox.
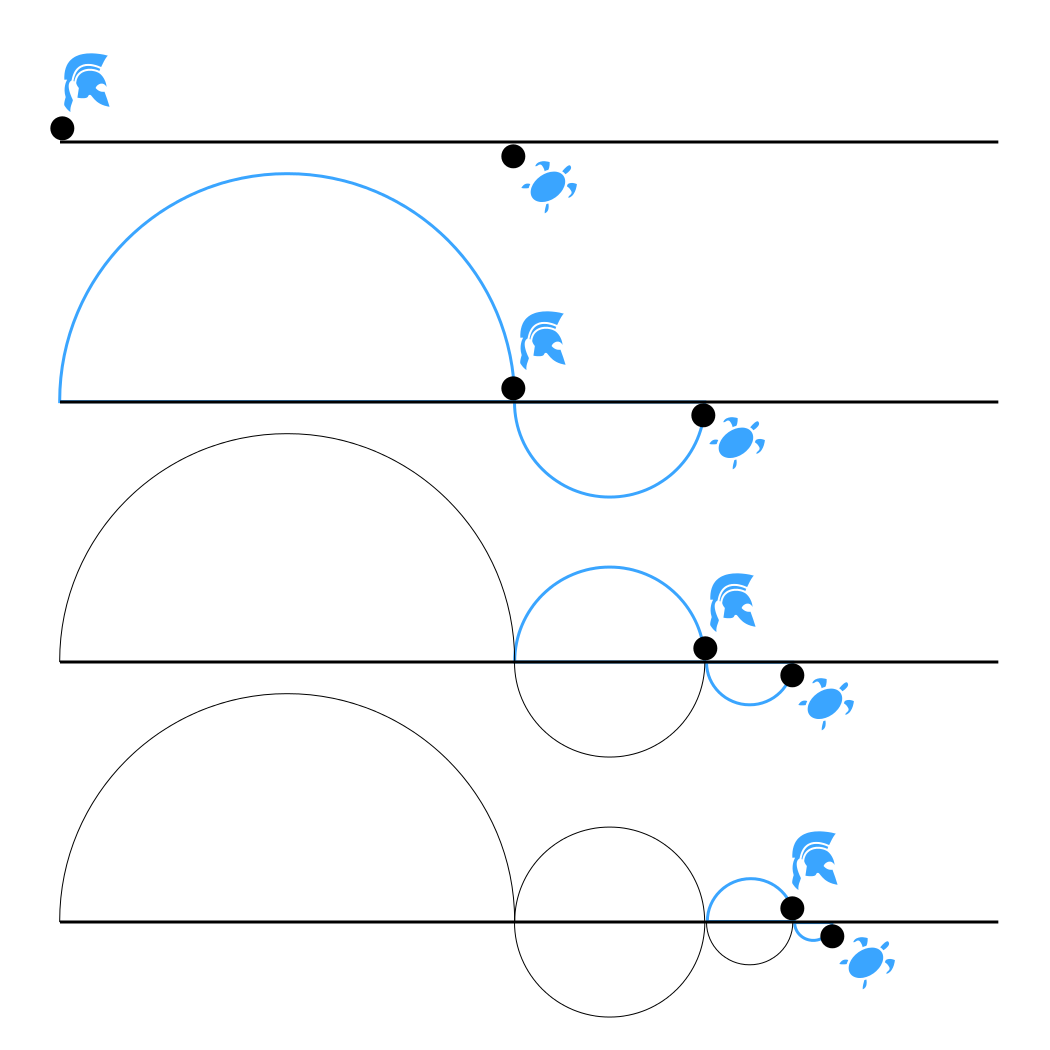
Achilles and the tortoise
 In the paradox of Achilles and the tortoise,
In the paradox of Achilles and the tortoise, Achilles
In Greek mythology, Achilles ( ) or Achilleus () was a hero of the Trojan War who was known as being the greatest of all the Greek warriors. The central character in Homer's ''Iliad'', he was the son of the Nereids, Nereid Thetis and Peleus, ...
is in a footrace with a tortoise. Achilles allows the tortoise a head start of 100 meters, for example. Suppose that each racer starts running at some constant speed, one faster than the other. After some finite time, Achilles will have run 100 meters, bringing him to the tortoise's starting point. During this time, the tortoise has run a much shorter distance, say 2 meters. It will then take Achilles some further time to run that distance, by which time the tortoise will have advanced farther; and then more time still to reach this third point, while the tortoise moves ahead. Thus, whenever Achilles arrives somewhere the tortoise has been, he still has some distance to go before he can even reach the tortoise. As Aristotle noted, this argument is similar to the Dichotomy. It lacks, however, the apparent conclusion of motionlessness.
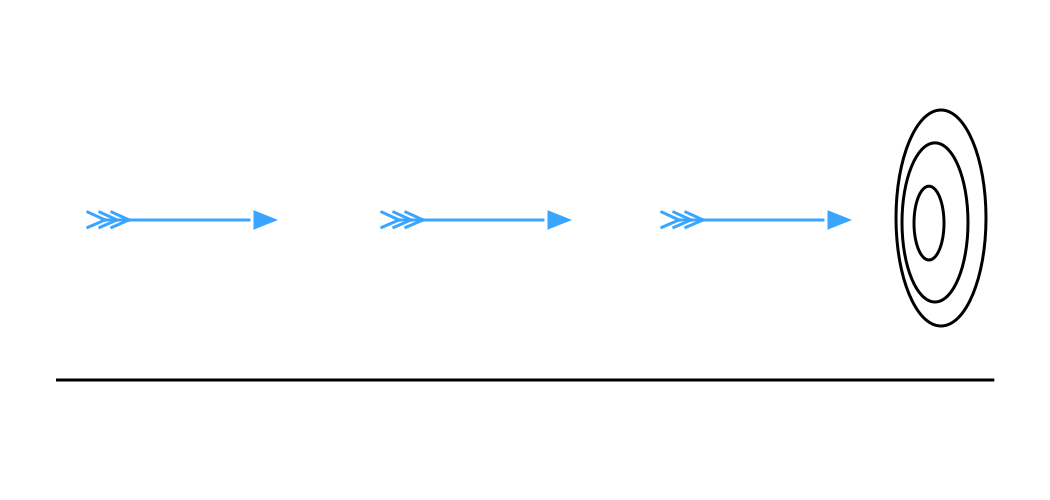
Arrow paradox
 In the arrow paradox, Zeno states that for motion to occur, an object must change the position which it occupies. He gives an example of an arrow in flight. He states that at any one (durationless) instant of time, the arrow is neither moving to where it is, nor to where it is not.
It cannot move to where it is not, because no time elapses for it to move there; it cannot move to where it is, because it is already there. In other words, at every instant of time there is no motion occurring. If everything is motionless at every instant, and time is entirely composed of instants, then motion is impossible.
Whereas the first two paradoxes divide space, this paradox starts by dividing time—and not into segments, but into points.
In the arrow paradox, Zeno states that for motion to occur, an object must change the position which it occupies. He gives an example of an arrow in flight. He states that at any one (durationless) instant of time, the arrow is neither moving to where it is, nor to where it is not.
It cannot move to where it is not, because no time elapses for it to move there; it cannot move to where it is, because it is already there. In other words, at every instant of time there is no motion occurring. If everything is motionless at every instant, and time is entirely composed of instants, then motion is impossible.
Whereas the first two paradoxes divide space, this paradox starts by dividing time—and not into segments, but into points.
Other paradoxes
Aristotle gives three other paradoxes.Paradox of place
From Aristotle:Paradox of the grain of millet
Description of the paradox from the ''Routledge Dictionary of Philosophy'': Aristotle's response: Description from Nick Huggett:The moving rows (or stadium)
 From Aristotle:
An expanded account of Zeno's arguments, as presented by Aristotle, is given in Simplicius's commentary ''On Aristotle's Physics''.
According to Angie Hobbs of The University of Sheffield, this paradox is intended to be considered together with the paradox of Achilles and the Tortoise, problematizing the concept of discrete space & time where the other problematizes the concept of infinitely divisible space & time.
From Aristotle:
An expanded account of Zeno's arguments, as presented by Aristotle, is given in Simplicius's commentary ''On Aristotle's Physics''.
According to Angie Hobbs of The University of Sheffield, this paradox is intended to be considered together with the paradox of Achilles and the Tortoise, problematizing the concept of discrete space & time where the other problematizes the concept of infinitely divisible space & time.
Proposed solutions
In classical antiquity
According to Simplicius, Diogenes the Cynic said nothing upon hearing Zeno's arguments, but stood up and walked, in order to demonstrate the falsity of Zeno's conclusions. To fully solve any of the paradoxes, however, one needs to show what is wrong with the argument, not just the conclusions. Throughout history several solutions have been proposed, among the earliest recorded being those of Aristotle and Archimedes. Aristotle remarked that as the distance decreases, the time needed to cover those distances also decreases, so that the time needed also becomes increasingly small. Aristotle also distinguished "things infinite in respect of divisibility" (such as a unit of space that can be mentally divided into ever smaller units while remaining spatially the same) from things (or distances) that are infinite in extension ("with respect to their extremities"). Aristotle's objection to the arrow paradox was that "Time is not composed of indivisible nows any more than any other magnitude is composed of indivisibles."Thomas Aquinas
Thomas Aquinas ( ; ; – 7 March 1274) was an Italian Dominican Order, Dominican friar and Catholic priest, priest, the foremost Scholasticism, Scholastic thinker, as well as one of the most influential philosophers and theologians in the W ...
, commenting on Aristotle's objection, wrote "Instants are not parts of time, for time is not made up of instants any more than a magnitude is made of points, as we have already proved. Hence it does not follow that a thing is not in motion in a given time, just because it is not in motion in any instant of that time."
In modern mathematics
Some mathematicians and historians, such as Carl Benjamin Boyer, hold that Zeno's paradoxes are simply mathematical problems, for which modern calculus provides a mathematical solution. Infinite processes remained theoretically troublesome in mathematics until the late 19th century. With theepsilon-delta
Although the function is not defined at zero, as becomes closer and closer to zero, becomes arbitrarily close to 1. In other words, the limit of as approaches zero, equals 1.
In mathematics, the limit of a function is a fundame ...
definition of limit, Karl Weierstrass
Karl Theodor Wilhelm Weierstrass (; ; 31 October 1815 – 19 February 1897) was a German mathematician often cited as the " father of modern analysis". Despite leaving university without a degree, he studied mathematics and trained as a school t ...
and Augustin-Louis Cauchy
Baron Augustin-Louis Cauchy ( , , ; ; 21 August 1789 – 23 May 1857) was a French mathematician, engineer, and physicist. He was one of the first to rigorously state and prove the key theorems of calculus (thereby creating real a ...
developed a rigorous formulation of the logic and calculus involved. These works resolved the mathematics involving infinite processes. B Russell (1956) ''Mathematics and the metaphysicians'' in "The World of Mathematics" (ed. J R Newman), pp 1576-1590.
Some philosophers, however, say that Zeno's paradoxes and their variations (see Thomson's lamp) remain relevant metaphysical
Metaphysics is the branch of philosophy that examines the basic structure of reality. It is traditionally seen as the study of mind-independent features of the world, but some theorists view it as an inquiry into the conceptual framework of h ...
problems. While mathematics can calculate where and when the moving Achilles will overtake the Tortoise of Zeno's paradox, philosophers such as Kevin Brown and Francis Moorcroft hold that mathematics does not address the central point in Zeno's argument, and that solving the mathematical issues does not solve every issue the paradoxes raise. Brown concludes "Given the history of 'final resolutions', from Aristotle onwards, it's probably foolhardy to think we've reached the end. It may be that Zeno's arguments on motion, because of their simplicity and universality, will always serve as a kind of ' Rorschach image' onto which people can project their most fundamental phenomenological concerns (if they have any)."
Henri Bergson
An alternative conclusion, proposed byHenri Bergson
Henri-Louis Bergson (; ; 18 October 1859 – 4 January 1941) was a French philosopher who was influential in the traditions of analytic philosophy and continental philosophy, especially during the first half of the 20th century until the S ...
in his 1896 book '' Matter and Memory'', is that, while the path is divisible, the motion is not.
Peter Lynds
In 2003, Peter Lynds argued that all of Zeno's motion paradoxes are resolved by the conclusion that instants in time and instantaneous magnitudes do not physically exist.Time’s Up, Einstein, Josh McHugh,
Wired Magazine
''Wired'' is a bi-monthly American magazine that focuses on how emerging technologies affect culture, the economy, and politics. It is published in both print and Online magazine, online editions by Condé Nast. The magazine has been in public ...
, June 2005 Lynds argues that an object in relative motion cannot have an instantaneous or determined relative position (for if it did, it could not be in motion), and so cannot have its motion fractionally dissected as if it does, as is assumed by the paradoxes. Nick Huggett argues that Zeno is assuming the conclusion when he says that objects that occupy the same space as they do at rest must be at rest.
Bertrand Russell
Based on the work ofGeorg Cantor
Georg Ferdinand Ludwig Philipp Cantor ( ; ; – 6 January 1918) was a mathematician who played a pivotal role in the creation of set theory, which has become a foundations of mathematics, fundamental theory in mathematics. Cantor establi ...
, Bertrand Russell
Bertrand Arthur William Russell, 3rd Earl Russell, (18 May 1872 – 2 February 1970) was a British philosopher, logician, mathematician, and public intellectual. He had influence on mathematics, logic, set theory, and various areas of analytic ...
offered a solution to the paradoxes, what is known as the "at-at theory of motion". It agrees that there can be no motion "during" a durationless instant, and contends that all that is required for motion is that the arrow be at one point at one time, at another point another time, and at appropriate points between those two points for intervening times. In this view motion is just change in position over time.
Hermann Weyl
Another proposed solution is to question one of the assumptions Zeno used in his paradoxes (particularly the Dichotomy), which is that between any two different points in space (or time), there is always another point. Without this assumption there are only a finite number of distances between two points, hence there is no infinite sequence of movements, and the paradox is resolved. According toHermann Weyl
Hermann Klaus Hugo Weyl (; ; 9 November 1885 – 8 December 1955) was a German mathematician, theoretical physicist, logician and philosopher. Although much of his working life was spent in Zürich, Switzerland, and then Princeton, New Jersey, ...
, the assumption that space is made of finite and discrete units is subject to a further problem, given by the " tile argument" or "distance function problem". According to this, the length of the hypotenuse of a right angled triangle in discretized space is always equal to the length of one of the two sides, in contradiction to geometry. Jean Paul Van Bendegem has argued that the Tile Argument can be resolved, and that discretization can therefore remove the paradox.
Applications
Quantum Zeno effect
In 1977, physicists E. C. George Sudarshan and B. Misra discovered that the dynamical evolution (motion
In physics, motion is when an object changes its position with respect to a reference point in a given time. Motion is mathematically described in terms of displacement, distance, velocity, acceleration, speed, and frame of reference to an o ...
) of a quantum system
Quantum mechanics is the fundamental physical Scientific theory, theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is ...
can be hindered (or even inhibited) through observation
Observation in the natural sciences is an act or instance of noticing or perceiving and the acquisition of information from a primary source. In living beings, observation employs the senses. In science, observation can also involve the percep ...
of the system
A system is a group of interacting or interrelated elements that act according to a set of rules to form a unified whole. A system, surrounded and influenced by its open system (systems theory), environment, is described by its boundaries, str ...
.
This effect is usually called the quantum Zeno effect as it is strongly reminiscent of Zeno's arrow paradox. This effect was first theorized in 1958.
Zeno behaviour
In the field of verification and design of timed and hybrid systems, the system behaviour is called ''Zeno'' if it includes an infinite number of discrete steps in a finite amount of time. Someformal verification
In the context of hardware and software systems, formal verification is the act of proving or disproving the correctness of a system with respect to a certain formal specification or property, using formal methods of mathematics.
Formal ver ...
techniques exclude these behaviours from analysis, if they are not equivalent to non-Zeno behaviour. In systems design these behaviours will also often be excluded from system models, since they cannot be implemented with a digital controller.
Similar paradoxes
School of Names
 Roughly contemporaneously during the
Roughly contemporaneously during the Warring States period
The Warring States period in history of China, Chinese history (221 BC) comprises the final two and a half centuries of the Zhou dynasty (256 BC), which were characterized by frequent warfare, bureaucratic and military reforms, and ...
(475–221 BCE), ancient Chinese philosophers from the School of Names, a school of thought similarly concerned with logic and dialectics, developed paradoxes similar to those of Zeno. The works of the School of Names have largely been lost, with the exception of portions of the ''Gongsun Longzi''. The second of the Ten Theses of Hui Shi suggests knowledge of infinitesimals:''That which has no thickness cannot be piled up; yet it is a thousand li in dimension.'' Among the many puzzles of his recorded in the ''Zhuangzi'' is one very similar to Zeno's Dichotomy: The Mohist canon appears to propose a solution to this paradox by arguing that in moving across a measured length, the distance is not covered in successive fractions of the length, but in one stage. Due to the lack of surviving works from the School of Names, most of the other paradoxes listed are difficult to interpret.
In popular culture
" What the Tortoise Said to Achilles", written in 1895 byLewis Carroll
Charles Lutwidge Dodgson (27 January 1832 – 14 January 1898), better known by his pen name Lewis Carroll, was an English author, poet, mathematician, photographer and reluctant Anglicanism, Anglican deacon. His most notable works are ''Alice ...
, describes a paradoxical infinite regress argument in the realm of pure logic. It uses Achilles and the Tortoise as characters in a clear reference to Zeno's paradox of Achilles.
See also
* Incommensurable magnitudes * Infinite regress * Philosophy of space and time *Renormalization
Renormalization is a collection of techniques in quantum field theory, statistical field theory, and the theory of self-similar geometric structures, that is used to treat infinities arising in calculated quantities by altering values of the ...
* Ross–Littlewood paradox
* Supertask
* Zeno machine
* List of paradoxes
This list includes well known paradoxes, grouped thematically. The grouping is approximate, as paradoxes may fit into more than one category. This list collects only scenarios that have been called a paradox by at least one source and have their ...
Notes
References
* Kirk, G. S., J. E. Raven, M. Schofield (1984) ''The Presocratic Philosophers: A Critical History with a Selection of Texts, 2nd ed.''Cambridge University Press
Cambridge University Press was the university press of the University of Cambridge. Granted a letters patent by King Henry VIII in 1534, it was the oldest university press in the world. Cambridge University Press merged with Cambridge Assessme ...
. .
*
* Plato
Plato ( ; Greek language, Greek: , ; born BC, died 348/347 BC) was an ancient Greek philosopher of the Classical Greece, Classical period who is considered a foundational thinker in Western philosophy and an innovator of the writte ...
(1926) ''Plato: Cratylus. Parmenides. Greater Hippias. Lesser Hippias'', H. N. Fowler (Translator), Loeb Classical Library
The Loeb Classical Library (LCL; named after James Loeb; , ) is a monographic series of books originally published by Heinemann and since 1934 by Harvard University Press. It has bilingual editions of ancient Greek and Latin literature, ...
. .
* Sainsbury, R.M. (2003) ''Paradoxes'', 2nd ed. Cambridge University Press. .
*
External links
* Dowden, Bradley.Zeno’s Paradoxes
" Entry in the
Internet Encyclopedia of Philosophy
The ''Internet Encyclopedia of Philosophy'' (''IEP'') is a scholarly online encyclopedia with around 900 articles about philosophy, philosophers, and related topics. The IEP publishes only peer review, peer-reviewed and blind-refereed original p ...
.
*
Introduction to Mathematical Philosophy
Ludwig-Maximilians-Universität München * Silagadze, Z. K.
Zeno meets modern science
" *
Zeno's Paradox: Achilles and the Tortoise
' by Jon McLoone,
Wolfram Demonstrations Project
The Wolfram Demonstrations Project is an Open source, open-source collection of Interactive computing, interactive programmes called Demonstrations. It is hosted by Wolfram Research. At its launch, it contained 1300 demonstrations but has grown t ...
.
Kevin Brown on Zeno and the Paradox of Motion
* * * {{authority control Eponymous paradoxes Philosophical paradoxes Supertasks Mathematical paradoxes Paradoxes of infinity Physical paradoxes