Wigner–Ville Distribution

The Wigner quasiprobability distribution (also called the Wigner function or the Wigner–Ville distribution, after Eugene Wigner and Jean-André Ville) is a quasiprobability distribution. It was introduced by Eugene Wigner in 1932 to study quantum corrections to classical statistical mechanics. The goal was to link the wavefunction that appears in Schrödinger's equation to a probability distribution in phase space.

It is a generating function for all spatial autocorrelation functions of a given quantum-mechanical wavefunction .
Thus, it maps on the quantum density matrix in the map between real phase-space functions and Hermitian operators introduced by Hermann Weyl in 1927, in a context related to representation theory in mathematics (see Weyl quantization). In effect, it is the Wigner–Weyl transform of the density matrix, so the realization of that operator in phase space. It was later rederived by Jean Ville in 1948 as a quadratic (in signal) representation of the local time-frequency energy of a signal, effectively a spectrogram.

In 1949, José Enrique Moyal, who had derived it independently, recognized it as the quantum moment-generating functional, and thus as the basis of an elegant encoding of all quantum expectation values, and hence quantum mechanics, in phase space (see Phase-space formulation). It has applications in statistical mechanics, quantum chemistry, quantum optics, classical optics and signal analysis in diverse fields, such as electrical engineering, seismology, time–frequency analysis for music signals, spectrograms in biology and speech processing, and engine design.

Relation to classical mechanics

A classical particle has a definite position and momentum, and hence it is represented by a point in phase space. Given a collection (ensemble) of particles, the probability of finding a particle at a certain position in phase space is specified by a probability distribution, the Liouville density. This strict interpretation fails
for a quantum particle, due to the uncertainty principle. Instead, the above quasiprobability Wigner distribution plays an analogous role, but does not satisfy all the properties of a conventional probability distribution; and, conversely, satisfies boundedness properties unavailable to classical distributions.

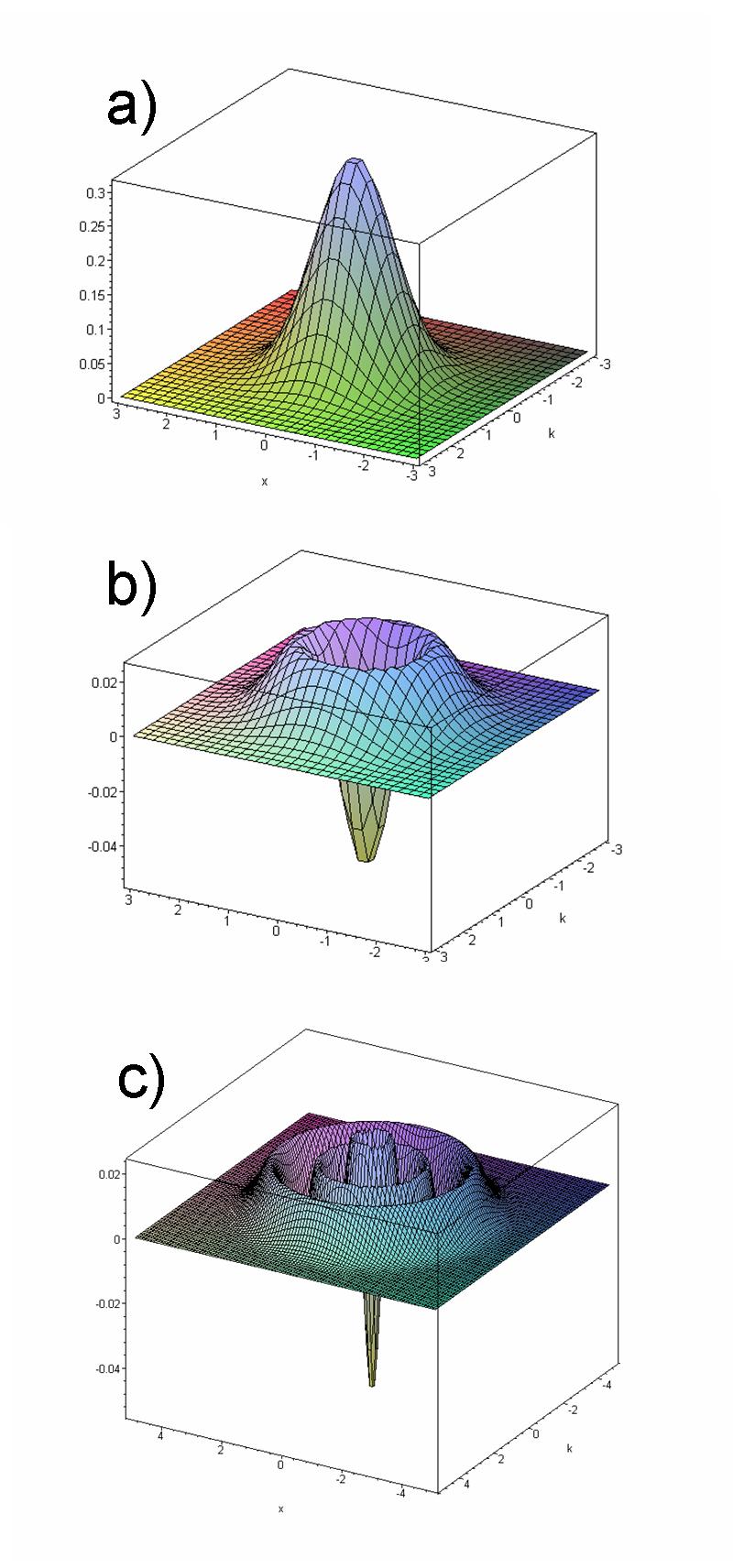
For instance, the Wigner distribution can and normally does take on negative values for states which have no classical model—and is a convenient indicator of quantum-mechanical interference. (See below for a characterization of pure states whose Wigner functions are non-negative.)
Smoothing the Wigner distribution through a filter of size larger than (e.g., convolving with a
phase-space Gaussian, a Weierstrass transform, to yield the Husimi representation, below), results in a positive-semidefinite function, i.e., it may be thought to have been coarsened to a semi-classical one.

Regions of such negative value are provable (by convolving them with a small Gaussian) to be "small": they cannot extend to compact regions larger than a few , and hence disappear in the classical limit. They are shielded by the uncertainty principle, which does not allow precise location within phase-space regions smaller than , and thus renders such " negative probabilities" less paradoxical.

Definition and meaning

The Wigner distribution of a pure state is defined as

where is the wavefunction, and and are position and momentum, but could be any conjugate variable pair (e.g. real and imaginary parts of the electric field or frequency and time of a signal). Note that it may have support in even in regions where has no support in ("beats").

It is symmetric in and :
: $W(x, p) = \frac \int_^\infty \varphi^*(p + q) \varphi(p - q) e^ \,dq,$
where is the normalized momentum-space wave function, proportional to the Fourier transform of .

In 3D,
: $W(\vec, \vec) = \frac \int \psi^*(\vec + \hbar\vec/2) \psi(\vec - \hbar\vec/2) e^ \,d^3 s.$

In the general case, which includes mixed states, it is the Wigner transform of the density matrix:
: $W(x, p) = \frac \int_^\infty \langle x - y, \hat , x + y \rangle e^ \,dy,$
where ⟨''x'', ''ψ''⟩ = . This Wigner transformation (or map) is the inverse of the Weyl transform, which maps phase-space functions to Hilbert-space operators, in Weyl quantization.

Thus, the Wigner function is the cornerstone of quantum mechanics in phase space.

In 1949, José Enrique Moyal elucidated how the Wigner function provides the integration measure (analogous to a probability density function) in phase space, to yield expectation values from phase-space c-number functions uniquely associated to suitably ordered operators through Weyl's transform (see Wigner–Weyl transform and property 7 below), in a manner evocative of classical probability theory.

Specifically, an operator's expectation value is a "phase-space average" of the Wigner transform of that operator:
: $\langle \hat \rangle = \int dx\,dp\, W(x, p) g(x, p).$

Mathematical properties

1. ''W''(''x'', ''p'') is a real-valued function.

2. The ''x'' and ''p'' probability distributions are given by the marginals:
:: $\int_^\infty dp\, W(x, p) = \langle x, \hat, x \rangle.$ If the system can be described by a pure state, one gets $\int_^\infty dp\, W(x, p) = , \psi(x), ^2.$
:: $\int_^\infty dx\, W(x, p) = \langle p, \hat, p \rangle.$ If the system can be described by a pure state, one has $\int_^ dx\, W(x, p) = , \varphi(p), ^2.$
:: $\int_^\infty dx \int_^\infty dp\, W(x, p) = \operatorname(\hat).$
: Typically the trace of the density matrix ''$\hat$'' is equal to 1.

3. ''W''(''x'', ''p'') has the following reflection symmetries:
:* Time symmetry: $\psi(x) \to \psi(x)^* \Rightarrow W(x, p) \to W(x, -p).$
:* Space symmetry: $\psi(x) \to \psi(-x) \Rightarrow W(x, p) \to W(-x, -p).$

4. ''W''(''x'', ''p'') is Galilei-covariant:
:: $\psi(x) \to \psi(x + y) \Rightarrow W(x, p) \to W(x + y, p).$
: It is not Lorentz-covariant.

5. The equation of motion for each point in the phase space is classical in the absence of forces:
:: $\frac = \frac \frac.$
: In fact, it is classical even in the presence of harmonic forces.

6. State overlap is calculated as
:: $, \langle \psi, \theta \rangle, ^2 = 2\pi\hbar \int_^\infty dx \int_^\infty dp\, W_\psi(x, p) W_\theta(x, p).$

7. Operator expectation values (averages) are calculated as phase-space averages of the respective Wigner transforms:
:: $g(x, p) \equiv \int_^\infty dy\, \left\langle x - \frac \ \hat \left, x + \frac \right\rangle e^,$
:: $\langle \psi, \hat, \psi\rangle = \operatorname(\hat \hat) = \int_^\infty dx \int_^\infty dp\, W(x, p) g(x, p).$

8. For ''W''(''x'', ''p'') to represent physical (positive) density matrices, it must satisfy
:: $\int_^\infty dx\, \int_^\infty dp\, W(x, p) W_\theta(x, p) \ge 0$
: for all pure states , θ⟩.

9. By virtue of the Cauchy–Schwarz inequality, for a pure state, it is constrained to be bounded:
:: $-\frac 2 h \leq W(x, p) \leq \frac 2 h.$
: This bound disappears in the classical limit, ''ħ'' → 0. In this limit, ''W''(''x'', ''p'') reduces to the probability density in coordinate space ''x'', usually highly localized, multiplied by δ-functions in momentum: the classical limit is "spiky". Thus, this quantum-mechanical bound precludes a Wigner function which is a perfectly localized δ-function in phase space, as a reflection of the uncertainty principle.

10. The Wigner transformation is simply the Fourier transform of the antidiagonals of the density matrix, when that matrix is expressed in a position basis.

Examples

Let $, m\rangle \equiv \frac , 0\rangle$ be the $m$-th Fock state of a quantum harmonic oscillator. Groenewold (1946) discovered its associated Wigner function, in dimensionless variables:
: $W_(x, p) = \frac e^ L_m\big(2(p^2 + x^2)\big),$
where $L_m(x)$ denotes the $m$-th Laguerre polynomial.

This may follow from the expression for the static eigenstate wavefunctions,
: $u_m(x) = \pi^ H_m(x) e^,$
where $H_m$ is the $m$-th Hermite polynomial. From the above definition of the Wigner function, upon a change of integration variables,
: $W_(x, p) = \frac e^ \int_^\infty d\zeta\, e^ H_m(\zeta - ip + x) H_m(\zeta - ip - x).$
The expression then follows from the integral relation between Hermite and Laguerre polynomials.

Evolution equation for Wigner function

The Wigner transformation is a general invertible transformation of an operator on a Hilbert space to a function ''g''(''x'', ''p'') on phase space and is given by
: $g(x, p) = \int_^\infty ds\, e^ \left\langle x - \frac s2\ \hat G \left, x + \frac s2\right\rangle.$

Hermitian operators map to real functions. The inverse of this transformation, from phase space to Hilbert space, is called the Weyl transformation:
: $\langle x , \hat G , y \rangle = \int_^\infty \frac e^ g\left(\frac, p\right)$
(not to be confused with the distinct Weyl transformation in differential geometry).

The Wigner function discussed here is thus seen to be the Wigner transform of the density matrix operator ''ρ̂''. Thus the trace of an operator with the density matrix Wigner-transforms to the equivalent phase-space integral overlap of with the Wigner function.

The Wigner transform of the von Neumann evolution equation of the density matrix in the Schrödinger picture is Moyal's evolution equation for the Wigner function:

where is the Hamiltonian, and is the Moyal bracket. In the classical limit, , the Moyal bracket reduces to the Poisson bracket, while this evolution equation reduces to the Liouville equation of classical statistical mechanics.

Formally, the classical Liouville equation can be solved in terms of the phase-space particle trajectories which are solutions of the classical Hamilton equations. This technique of solving partial differential equations is known as the method of characteristics. This method transfers to quantum systems, where the characteristics' "trajectories" now determine the evolution of Wigner functions. The solution of the Moyal evolution equation for the Wigner function is represented formally as
: $W(x, p, t) = W\big(\star\big(x_(x, p), p_(x, p)\big), 0\big),$
where $x_t(x, p)$ and $p_t(x, p)$ are the characteristic trajectories subject to the quantum Hamilton equations with initial conditions $x_(x, p) = x$ and $p_(x, p) = p$, and where $\star$-product composition is understood for all argument functions.

Since $\star$-composition of functions is ''thoroughly nonlocal'' (the "quantum probability fluid" diffuses, as observed by Moyal), vestiges of local trajectories in quantum systems are barely discernible in the evolution of the Wigner distribution function. In the integral representation of $\star$-products, successive operations by them have been adapted to a phase-space path integral, to solve the evolution equation for the Wigner function (see also B. Segev: ''Evolution kernels for phase space distributions''. In: See especially section 5. "Path integral for the propagator" o
pages 86–89

Als
online
). This non-local feature of Moyal time evolution is illustrated in the gallery below, for Hamiltonians more complex than the harmonic oscillator. In the classical limit, the trajectory nature of the time evolution of Wigner functions becomes more and more distinct. At ''ħ'' = 0, the characteristics' trajectories reduce to the classical trajectories of particles in phase space.

Harmonic-oscillator time evolution

In the special case of the quantum harmonic oscillator, however, the evolution is simple and appears identical to the classical motion: a rigid rotation in phase space with a frequency given by the oscillator frequency. This is illustrated in the gallery below. This same time evolution occurs with quantum states of light modes, which are harmonic oscillators.

Classical limit

The Wigner function allows one to study the classical limit, offering a comparison of the classical and quantum dynamics in phase space.

It has been suggested that the Wigner function approach can be viewed as a quantum analogy to the operatorial formulation of classical mechanics introduced in 1932 by Bernard Koopman and John von Neumann: the time evolution of the Wigner function approaches, in the limit ''ħ'' → 0, the time evolution of the Koopman–von Neumann wavefunction of a classical particle.

Positivity of the Wigner function

As already noted, the Wigner function of quantum state typically takes some negative values. Indeed, for a pure state in one variable, if $W(x, p) \ge 0$ for all $x$ and $p$, then the wave function must have the form
: $\psi(x) = e^$
for some complex numbers $a, b, c$ with $\operatorname(a) > 0$ (Hudson's theorem). Note that $a$ is allowed to be complex, so that $\psi$ is not necessarily a Gaussian wave packet in the usual sense. Thus, pure states with non-negative Wigner functions are not necessarily minimum-uncertainty states in the sense of the Heisenberg uncertainty formula; rather, they give equality in the Schrödinger uncertainty formula, which includes an anticommutator term in addition to the commutator term. (With careful definition of the respective variances, all pure-state Wigner functions lead to Heisenberg's inequality all the same.)

In higher dimensions, the characterization of pure states with non-negative Wigner functions is similar; the wave function must have the form
: $\psi(x) = e^,$
where $A$ is a symmetric complex matrix whose real part is positive-definite, $b$ is a complex vector, and is a complex number.F. Soto and P. Claverie, "When is the Wigner function of multidimensional systems nonnegative?", ''Journal of Mathematical Physics'' 24 (1983) 97–100. The Wigner function of any such state is a Gaussian distribution on phase space.

Soto and Claverie give an elegant proof of this characterization, using the Segal–Bargmann transform. The reasoning is as follows. The Husimi Q function of $\psi$ may be computed as the squared magnitude of the Segal–Bargmann transform of $\psi$, multiplied by a Gaussian. Meanwhile, the Husimi Q function is the convolution of the Wigner function with a Gaussian. If the Wigner function of $\psi$ is non-negative everywhere on phase space, then the Husimi Q function will be strictly positive everywhere on phase space. Thus, the Segal–Bargmann transform $F(x + ip)$ of $\psi$ will be nowhere zero. Thus, by a standard result from complex analysis, we have
: $F(x + ip) = e^$
for some holomorphic function $g$. But in order for $F$ to belong to the Segal–Bargmann space—that is, for $F$ to be square-integrable with respect to a Gaussian measure—$g$ must have at most quadratic growth at infinity. From this, elementary complex analysis can be used to show that $g$ must actually be a quadratic polynomial. Thus, we obtain an explicit form of the Segal–Bargmann transform of any pure state whose Wigner function is non-negative. We can then invert the Segal–Bargmann transform to obtain the claimed form of the position wave function.

There does not appear to be any simple characterization of mixed states with non-negative Wigner functions.

The Wigner function in relation to other interpretations of quantum mechanics

It has been shown that the Wigner quasiprobability distribution function can be regarded as an -deformation of another phase-space distribution function that describes an ensemble of de Broglie–Bohm causal trajectories. Basil Hiley has shown that the quasi-probability distribution may be understood as the density matrix re-expressed in terms of a mean position and momentum of a "cell" in phase space, and the de Broglie–Bohm interpretation allows one to describe the dynamics of the centers of such "cells".

There is a close connection between the description of quantum states in terms of the Wigner function and a method of quantum states reconstruction in terms of mutually unbiased bases.

Uses of the Wigner function outside quantum mechanics

* In the modelling of optical systems such as telescopes or fibre telecommunications devices, the Wigner function is used to bridge the gap between simple ray tracing and the full wave analysis of the system. Here is replaced with in the small-angle (paraxial) approximation. In this context, the Wigner function is the closest one can get to describing the system in terms of rays at position and angle while still including the effects of interference. If it becomes negative at any point, then simple ray tracing will not suffice to model the system. That is to say, negative values of this function are a symptom of the Gabor limit of the classical light signal and ''not'' of quantum features of light associated with .
* In signal analysis, a time-varying electrical signal, mechanical vibration, or sound wave are represented by a Wigner function. Here, is replaced with the time, and is replaced with the angular frequency , where is the regular frequency.
* In ultrafast optics, short laser pulses are characterized with the Wigner function using the same and substitutions as above. Pulse defects such as chirp (the change in frequency with time) can be visualized with the Wigner function. See adjacent figure.
* In quantum optics, and are replaced with the and quadratures, the real and imaginary components of the electric field (see coherent state).

Measurements of the Wigner function

* Quantum tomography
* Frequency-resolved optical gating

Other related quasiprobability distributions

The Wigner distribution was the first quasiprobability distribution to be formulated, but many more followed, formally equivalent and transformable to and from it (see Transformation between distributions in time–frequency analysis). As in the case of coordinate systems, on account of varying properties, several such have with various advantages for specific applications:
* Glauber P representation
* Husimi Q representation
Nevertheless, in some sense, the Wigner distribution holds a privileged position among all these distributions, since it is the ''only one'' whose requisite star-product drops out (integrates out by parts to effective unity) in the evaluation of expectation values, as illustrated above, and so ''can'' be visualized as a quasiprobability measure analogous to the classical ones.

Historical note

As indicated, the formula for the Wigner function was independently derived several times in different contexts. In fact, apparently, Wigner was unaware that even within the context of quantum theory, it had been introduced previously by Heisenberg and Dirac, albeit purely formally: these two missed its significance, and that of its negative values, as they merely considered it as an approximation to the full quantum description of a system such as the atom. (Incidentally, Dirac would later become Wigner's brother-in-law, marrying his sister Manci.) Symmetrically, in most of his legendary 18-month correspondence with Moyal in the mid-1940s, Dirac was unaware that Moyal's quantum-moment generating function was effectively the Wigner function, and it was Moyal who finally brought it to his attention.Ann Moyal, (2006)
"Maverick Mathematician: The Life and Science of J. E. Moyal"
ANU E-press, 2006, .

See also

* Heisenberg group
* Wigner–Weyl transform
* Phase space formulation
* Moyal bracket
* Negative probability
* Optical equivalence theorem
* Modified Wigner distribution function
* Cohen's class distribution function
* Wigner distribution function
* Transformation between distributions in time–frequency analysis
* Squeezed coherent state
* Bilinear time–frequency distribution
* Continuous-variable quantum information

Footnotes

References

Further reading

* M. Levanda and V. Fleurov, "Wigner quasi-distribution function for charged particles in classical electromagnetic fields", ''Annals of Physics'', 292, 199–231 (2001). .

External links

wigner
Wigner function implementation in QuTiP.

Quantum Optics Gallery


Sonogram Visible Speech
GPL-licensed freeware for the Wigner quasiprobability distribution of signal files.

{{DEFAULTSORT:Wigner Quasi-Probability Distribution
Continuous distributions
Concepts in physics
Mathematical physics
Exotic probabilities
Articles containing video clips
Quantum optics