|
Squeezed Coherent State
In physics, a squeezed coherent state is a quantum state that is usually described by two non-commuting observables having continuous spectra of eigenvalues. Examples are position x and momentum p of a particle, and the (dimension-less) electric field in the amplitude X (phase 0) and in the mode Y (phase 90°) of a light wave (the wave's quadratures). The product of the standard deviations of two such operators obeys the uncertainty principle: :\Delta x \Delta p \geq \frac2\; and \;\Delta X \Delta Y \geq \frac4 , respectively. Trivial examples, which are in fact not squeezed, are the ground state , 0\rangle of the quantum harmonic oscillator and the family of coherent states , \alpha\rangle. These states saturate the uncertainty above and have a symmetric distribution of the operator uncertainties with \Delta x_g = \Delta p_g in "natural oscillator units" and \Delta X_g = \Delta Y_g = 1/2. (In literature different normalizations for the quadrature amplitudes are u ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Physics
Physics is the natural science that studies matter, its fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which relates to the order of nature, or, in other words, to the regular succession of events." Physics is one of the most fundamental scientific disciplines, with its main goal being to understand how the universe behaves. "Physics is one of the most fundamental of the sciences. Scientists of all disciplines use the ideas of physics, including chemists who study the structure of molecules, paleontologists who try to reconstruct how dinosaurs walked, and climatologists who study how human activities affect the atmosphere and oceans. Physics is also the foundation of all engineering and technology. No engineer could design a flat-screen TV, an interplanetary spacecraft, or even a better mousetrap without first understanding the basic laws of physics ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wavepacket
In physics, a wave packet (or wave train) is a short "burst" or " envelope" of localized wave action that travels as a unit. A wave packet can be analyzed into, or can be synthesized from, an infinite set of component sinusoidal waves of different wavenumbers, with phases and amplitudes such that they interfere constructively only over a small region of space, and destructively elsewhere. Each component wave function, and hence the wave packet, are solutions of a wave equation. Depending on the wave equation, the wave packet's profile may remain constant (no dispersion, see figure) or it may change (dispersion) while propagating. Quantum mechanics ascribes a special significance to the wave packet; it is interpreted as a probability amplitude, its norm squared describing the probability density that a particle or particles in a particular state will be measured to have a given position or momentum. The wave equation is in this case the Schrödinger equation, and thro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Light Wave
In physics, electromagnetic radiation (EMR) consists of waves of the electromagnetic (EM) field, which propagate through space and carry momentum and electromagnetic radiant energy. It includes radio waves, microwaves, infrared, (visible) light, ultraviolet, X-rays, and gamma rays. All of these waves form part of the electromagnetic spectrum. Classically, electromagnetic radiation consists of electromagnetic waves, which are synchronized oscillations of electric and magnetic fields. Depending on the frequency of oscillation, different wavelengths of electromagnetic spectrum are produced. In a vacuum, electromagnetic waves travel at the speed of light, commonly denoted ''c''. In homogeneous, isotropic media, the oscillations of the two fields are perpendicular to each other and perpendicular to the direction of energy and wave propagation, forming a transverse wave. The position of an electromagnetic wave within the electromagnetic spectrum can be characterized by either it ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Noise
Quantum noise is noise arising from the indeterminate state of matter in accordance with fundamental principles of quantum mechanics, specifically the uncertainty principle and via zero-point energy fluctuations. Quantum noise is due to the apparently discrete nature of the small quantum constituents such as electrons, as well as the discrete nature of quantum effects, such as photocurrents. Quantified noise is similar to classical noise theory and will not always return an asymmetric spectral density. Shot noise as coined by J. Verdeyen is a form of quantum noise related to the statistics of photon counting, the discrete nature of electrons, and intrinsic noise generation in electronics. In contrast to shot noise, the quantum mechanical uncertainty principle sets a lower limit to a measurement. The uncertainty principle requires any amplifier or detector to have noise. Macroscopic manifestations of quantum phenomena are easily disturbed, so quantum noise is mainly observed i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
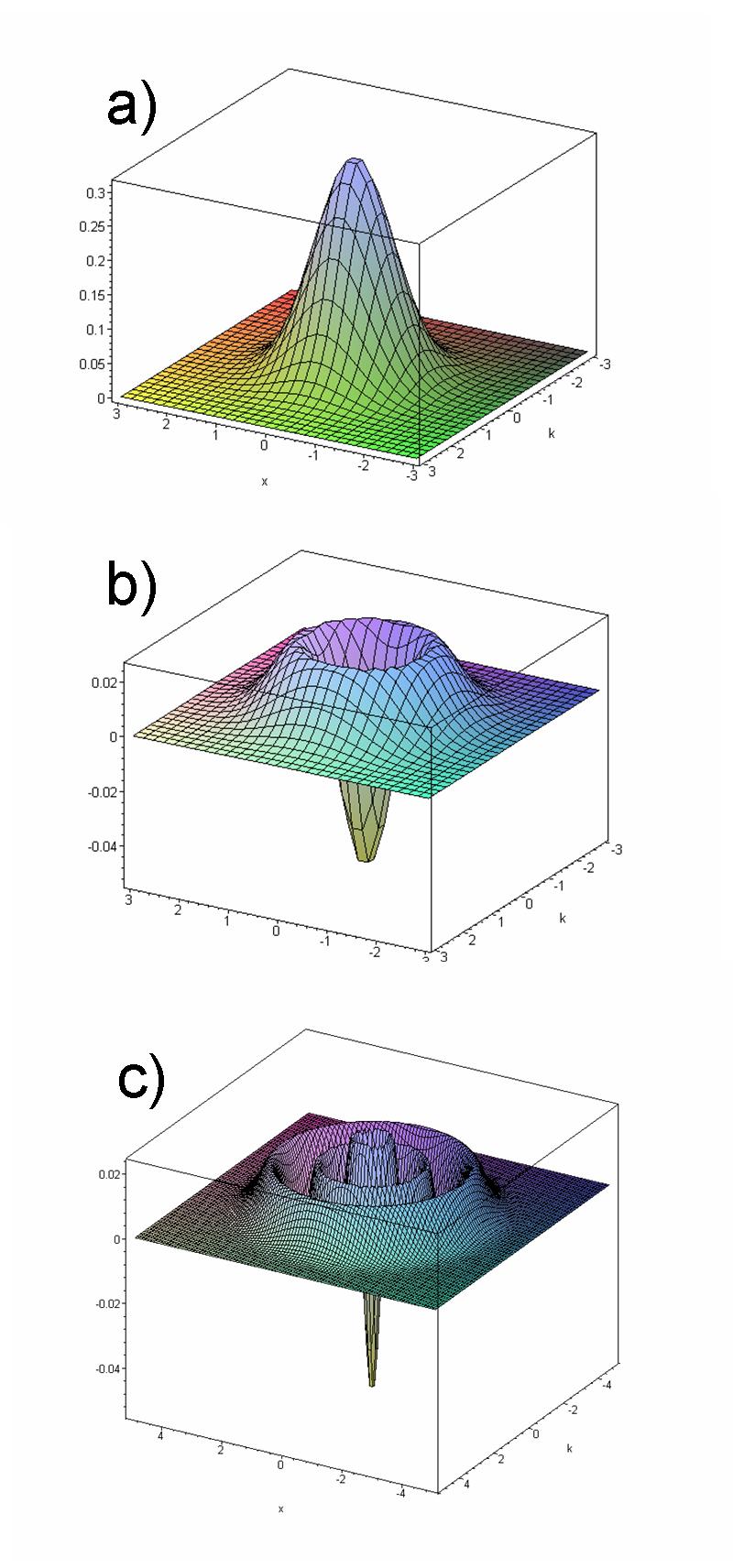
Wigner Quasiprobability Distribution
The Wigner quasiprobability distribution (also called the Wigner function or the Wigner–Ville distribution, after Eugene Wigner and Jean-André Ville) is a quasiprobability distribution. It was introduced by Eugene Wigner in 1932 to study quantum corrections to classical statistical mechanics. The goal was to link the wavefunction that appears in Schrödinger's equation to a probability distribution in phase space. It is a generating function for all spatial autocorrelation functions of a given quantum-mechanical wavefunction . Thus, it maps on the quantum density matrix in the map between real phase-space functions and Hermitian operators introduced by Hermann Weyl in 1927, in a context related to representation theory in mathematics (see Weyl quantization). In effect, it is the Wigner–Weyl transform of the density matrix, so the realization of that operator in phase space. It was later rederived by Jean Ville in 1948 as a quadratic (in signal) representation of the lo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complementarity (physics)
In physics, complementarity is a conceptual aspect of quantum mechanics that Niels Bohr regarded as an essential feature of the theory. The complementarity principle holds that objects have certain pairs of complementary properties which cannot all be observed or measured simultaneously. An example of such a pair is position and momentum. Bohr considered one of the foundational truths of quantum mechanics to be the fact that setting up an experiment to measure one quantity of a pair, for instance the position of an electron, excludes the possibility of measuring the other, yet understanding both experiments is necessary to characterize the object under study. In Bohr's view, the behavior of atomic and subatomic objects cannot be separated from the measuring instruments that create the context in which the measured objects behave. Consequently, there is no "single picture" that unifies the results obtained in these different experimental contexts, and only the "totality of the phe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Uncertainty Relation
In quantum mechanics, the uncertainty principle (also known as Heisenberg's uncertainty principle) is any of a variety of mathematical inequalities asserting a fundamental limit to the accuracy with which the values for certain pairs of physical quantities of a particle, such as position, ''x'', and momentum, ''p'', can be predicted from initial conditions. Such variable pairs are known as complementary variables or canonically conjugate variables; and, depending on interpretation, the uncertainty principle limits to what extent such conjugate properties maintain their approximate meaning, as the mathematical framework of quantum physics does not support the notion of simultaneously well-defined conjugate properties expressed by a single value. The uncertainty principle implies that it is in general not possible to predict the value of a quantity with arbitrary certainty, even if all initial conditions are specified. Introduced first in 1927 by the German physicist Werner H ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Werner Heisenberg
Werner Karl Heisenberg () (5 December 1901 – 1 February 1976) was a German theoretical physicist and one of the main pioneers of the theory of quantum mechanics. He published his work in 1925 in a breakthrough paper. In the subsequent series of papers with Max Born and Pascual Jordan, during the same year, his matrix formulation of quantum mechanics was substantially elaborated. He is known for the uncertainty principle, which he published in 1927. Heisenberg was awarded the 1932 Nobel Prize in Physics "for the creation of quantum mechanics". Heisenberg also made contributions to the theories of the hydrodynamics of turbulent flows, the atomic nucleus, ferromagnetism, cosmic rays, and subatomic particles. He was a principal scientist in the German nuclear weapons program during World War II. He was also instrumental in planning the first West German nuclear reactor at Karlsruhe, together with a research reactor in Munich, in 1957. Following World War II, he was appoint ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heisenberg Uncertainty Principle
In quantum mechanics, the uncertainty principle (also known as Heisenberg's uncertainty principle) is any of a variety of mathematical inequalities asserting a fundamental limit to the accuracy with which the values for certain pairs of physical quantities of a particle, such as position, ''x'', and momentum, ''p'', can be predicted from initial conditions. Such variable pairs are known as complementary variables or canonically conjugate variables; and, depending on interpretation, the uncertainty principle limits to what extent such conjugate properties maintain their approximate meaning, as the mathematical framework of quantum physics does not support the notion of simultaneously well-defined conjugate properties expressed by a single value. The uncertainty principle implies that it is in general not possible to predict the value of a quantity with arbitrary certainty, even if all initial conditions are specified. Introduced first in 1927 by the German physicist Werner ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Squeeze Operator
In quantum physics, the squeeze operator for a single mode of the electromagnetic field is :\hat(z) = \exp \left ( (z^* \hat^2 - z \hat^) \right ) , \qquad z = r \, e^ where the operators inside the exponential are the ladder operators. It is a unitary operator and therefore obeys S(\zeta)S^\dagger (\zeta)=S^\dagger (\zeta)S(\zeta)=\hat 1, where \hat 1 is the identity operator. Its action on the annihilation and creation operators produces :\hat^(z)\hat\hat(z)=\hat\cosh r - e^ \hat^ \sinh r \qquad\text\qquad \hat^(z)\hat^\hat(z)=\hat^\cosh r - e^ \hat \sinh r The squeeze operator is ubiquitous in quantum optics and can operate on any state. For example, when acting upon the vacuum, the squeezing operator produces the squeezed vacuum state. The squeezing operator can also act on coherent states and produce squeezed coherent states. The squeezing operator does not commute with the displacement operator: : \hat(z) \hat(\alpha) \neq \hat(\alpha) \hat(z), nor does it commute ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Displacement Operator
In the quantum mechanics study of optical phase space, the displacement operator for one mode is the shift operator in quantum optics, :\hat(\alpha)=\exp \left ( \alpha \hat^\dagger - \alpha^\ast \hat \right ) , where \alpha is the amount of displacement in optical phase space, \alpha^* is the complex conjugate of that displacement, and \hat and \hat^\dagger are the lowering and raising operators, respectively. The name of this operator is derived from its ability to displace a localized state in phase space by a magnitude \alpha. It may also act on the vacuum state by displacing it into a coherent state. Specifically, \hat(\alpha), 0\rangle=, \alpha\rangle where , \alpha\rangle is a coherent state, which is an eigenstate of the annihilation (lowering) operator. Properties The displacement operator is a unitary operator, and therefore obeys \hat(\alpha)\hat^\dagger(\alpha)=\hat^\dagger(\alpha)\hat(\alpha)=\hat, where \hat is the identity operator. Since \hat^\dagger(\alpha)=\ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vacuum State
In quantum field theory, the quantum vacuum state (also called the quantum vacuum or vacuum state) is the quantum state with the lowest possible energy. Generally, it contains no physical particles. The word zero-point field is sometimes used as a synonym for the vacuum state of a quantized field which is completely individual. According to present-day understanding of what is called the vacuum state or the quantum vacuum, it is "by no means a simple empty space". According to quantum mechanics, the vacuum state is not truly empty but instead contains fleeting electromagnetic waves and particles that pop into and out of the quantum field. The QED vacuum of quantum electrodynamics (or QED) was the first vacuum of quantum field theory to be developed. QED originated in the 1930s, and in the late 1940s and early 1950s it was reformulated by Feynman, Tomonaga, and Schwinger, who jointly received the Nobel prize for this work in 1965. For a historical discussion, see fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |

.gif)