Vibrations on:
[Wikipedia]
[Google]
[Amazon]
Vibration is a mechanical phenomenon whereby 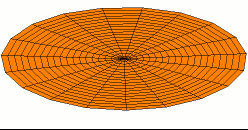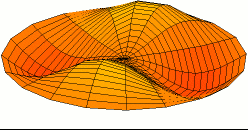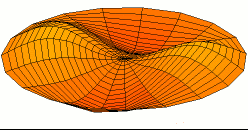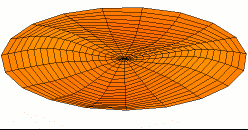

Where to place the control accelerometer: one of the most critical decisions in developing random vibration tests also is the most neglected
', EE-Evaluation Engineering, 2006 Other "response" points may experience higher vibration levels (resonance) or lower vibration level (anti-resonance or damping) than the control point(s). It is often desirable to achieve anti-resonance to keep a system from becoming too noisy, or to reduce strain on certain parts due to vibration modes caused by specific vibration frequencies. The most common types of vibration testing services conducted by vibration test labs are sinusoidal and random. Sine (one-frequency-at-a-time) tests are performed to survey the structural response of the device under test (DUT). During the early history of vibration testing, vibration machine controllers were limited only to controlling sine motion so only sine testing was performed. Later, more sophisticated analog and then digital controllers were able to provide random control (all frequencies at once). A random (all frequencies at once) test is generally considered to more closely replicate a real world environment, such as road inputs to a moving automobile. Most vibration testing is conducted in a 'single DUT axis' at a time, even though most real-world vibration occurs in various axes simultaneously. MIL-STD-810G, released in late 2008, Test Method 527, calls for multiple exciter testing. The ''vibration test fixtureTony Araujo.
The evolution of automotive vibration fixturing
', EE-Evaluation Engineering, 2019'' used to attach the DUT to the shaker table must be designed for the frequency range of the vibration test spectrum. It is difficult to design a vibration test fixture which duplicates the dynamic response (mechanical impedance)Blanks, H.S., "Equivalence Techniques for Vibration Testing," SVIC Notes, pp 17. of the actual in-use mounting. For this reason, to ensure repeatability between vibration tests, vibration fixtures are designed to be resonance free within the test frequency range. Generally for smaller fixtures and lower frequency ranges, the designer can target a fixture design that is free of resonances in the test frequency range. This becomes more difficult as the DUT gets larger and as the test frequency increases. In these cases multi-point control strategiesAraujo, T. and Yao, B., ''"Vibration Fixture Performance Qualification – A Review of Automotive Industry Best Practices," SAE Technical Paper 2020-01-1065, 2020, https://doi.org/10.4271/2020-01-1065.'' can mitigate some of the resonances that may be present in the future. Some vibration test methods limit the amount of crosstalk (movement of a response point in a mutually perpendicular direction to the axis under test) permitted to be exhibited by the vibration test fixture. Devices specifically designed to trace or record vibrations are called
 To start the investigation of the mass–spring–damper assume the damping is negligible and that there is no external force applied to the mass (i.e. free vibration). The force applied to the mass by the spring is proportional to the amount the spring is stretched "x" (assuming the spring is already compressed due to the weight of the mass). The proportionality constant, k, is the stiffness of the spring and has units of force/distance (e.g. lbf/in or N/m). The negative sign indicates that the force is always opposing the motion of the mass attached to it:
:
The force generated by the mass is proportional to the acceleration of the mass as given by
To start the investigation of the mass–spring–damper assume the damping is negligible and that there is no external force applied to the mass (i.e. free vibration). The force applied to the mass by the spring is proportional to the amount the spring is stretched "x" (assuming the spring is already compressed due to the weight of the mass). The proportionality constant, k, is the stiffness of the spring and has units of force/distance (e.g. lbf/in or N/m). The negative sign indicates that the force is always opposing the motion of the mass attached to it:
:
The force generated by the mass is proportional to the acceleration of the mass as given by  Assuming that the initiation of vibration begins by stretching the spring by the distance of ''A'' and releasing, the solution to the above equation that describes the motion of mass is:
:
This solution says that it will oscillate with
Assuming that the initiation of vibration begins by stretching the spring by the distance of ''A'' and releasing, the solution to the above equation that describes the motion of mass is:
:
This solution says that it will oscillate with
 When a "viscous" damper is added to the model this outputs a force that is proportional to the velocity of the mass. The damping is called viscous because it models the effects of a fluid within an object. The proportionality constant ''c'' is called the damping coefficient and has units of Force over velocity (lbf⋅s/in or N⋅s/m).
:
Summing the forces on the mass results in the following ordinary differential equation:
:
The solution to this equation depends on the amount of damping. If the damping is small enough, the system still vibrates—but eventually, over time, stops vibrating. This case is called underdamping, which is important in vibration analysis. If damping is increased just to the point where the system no longer oscillates, the system has reached the point of critical damping. If the damping is increased past critical damping, the system is
When a "viscous" damper is added to the model this outputs a force that is proportional to the velocity of the mass. The damping is called viscous because it models the effects of a fluid within an object. The proportionality constant ''c'' is called the damping coefficient and has units of Force over velocity (lbf⋅s/in or N⋅s/m).
:
Summing the forces on the mass results in the following ordinary differential equation:
:
The solution to this equation depends on the amount of damping. If the damping is small enough, the system still vibrates—but eventually, over time, stops vibrating. This case is called underdamping, which is important in vibration analysis. If damping is increased just to the point where the system no longer oscillates, the system has reached the point of critical damping. If the damping is increased past critical damping, the system is  The value of ''X'', the initial magnitude, and the
The value of ''X'', the initial magnitude, and the
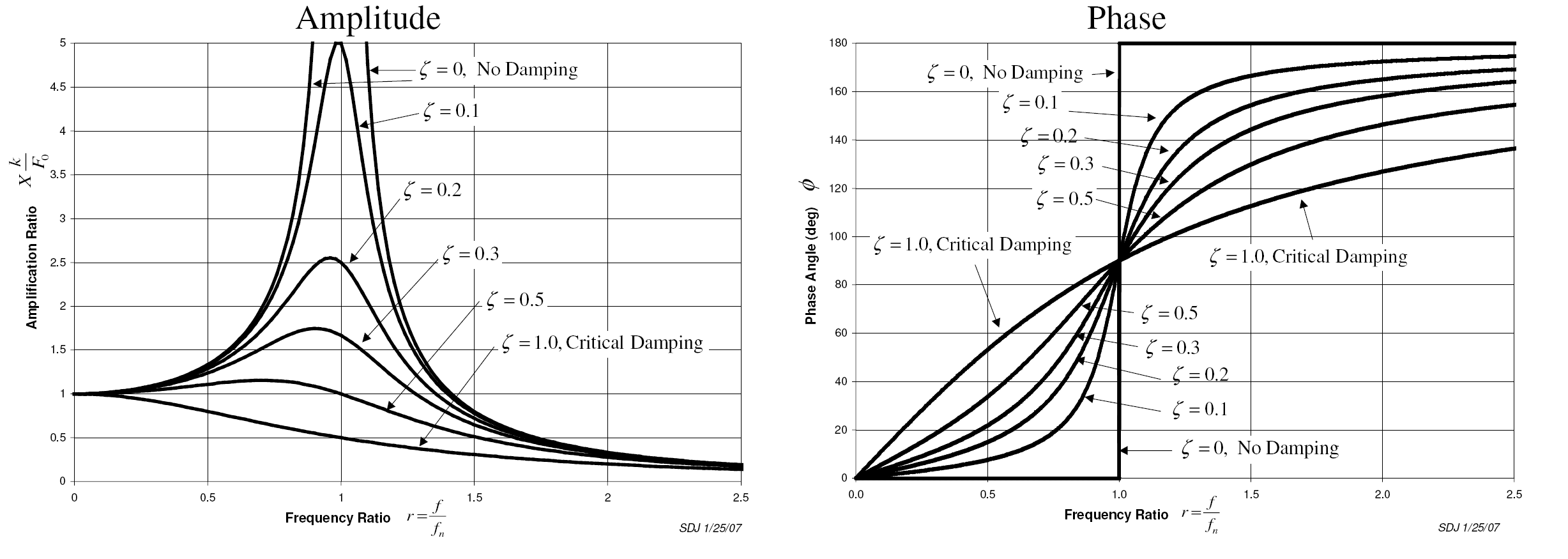 The plot of these functions, called "the frequency response of the system", presents one of the most important features in forced vibration. In a lightly damped system when the forcing frequency nears the natural frequency () the amplitude of the vibration can get extremely high. This phenomenon is called
The plot of these functions, called "the frequency response of the system", presents one of the most important features in forced vibration. In a lightly damped system when the forcing frequency nears the natural frequency () the amplitude of the vibration can get extremely high. This phenomenon is called
 The Fourier transform of the square wave generates a
The Fourier transform of the square wave generates a
 For example, calculating the FRF for a mass–spring–damper system with a mass of 1 kg, spring stiffness of 1.93 N/mm and a damping ratio of 0.1. The values of the spring and mass give a natural frequency of 7 Hz for this specific system. Applying the 1 Hz square wave from earlier allows the calculation of the predicted vibration of the mass. The figure illustrates the resulting vibration. It happens in this example that the fourth harmonic of the square wave falls at 7 Hz. The frequency response of the mass–spring–damper therefore outputs a high 7 Hz vibration even though the input force had a relatively low 7 Hz harmonic. This example highlights that the resulting vibration is dependent on both the forcing function and the system that the force is applied to.
The figure also shows the time domain representation of the resulting vibration. This is done by performing an inverse Fourier Transform that converts frequency domain data to time domain. In practice, this is rarely done because the frequency spectrum provides all the necessary information.
The frequency response function (FRF) does not necessarily have to be calculated from the knowledge of the mass, damping, and stiffness of the system—but can be measured experimentally. For example, if a known force over a range of frequencies is applied, and if the associated vibrations are measured, the frequency response function can be calculated, thereby characterizing the system. This technique is used in the field of experimental
For example, calculating the FRF for a mass–spring–damper system with a mass of 1 kg, spring stiffness of 1.93 N/mm and a damping ratio of 0.1. The values of the spring and mass give a natural frequency of 7 Hz for this specific system. Applying the 1 Hz square wave from earlier allows the calculation of the predicted vibration of the mass. The figure illustrates the resulting vibration. It happens in this example that the fourth harmonic of the square wave falls at 7 Hz. The frequency response of the mass–spring–damper therefore outputs a high 7 Hz vibration even though the input force had a relatively low 7 Hz harmonic. This example highlights that the resulting vibration is dependent on both the forcing function and the system that the force is applied to.
The figure also shows the time domain representation of the resulting vibration. This is done by performing an inverse Fourier Transform that converts frequency domain data to time domain. In practice, this is rarely done because the frequency spectrum provides all the necessary information.
The frequency response function (FRF) does not necessarily have to be calculated from the knowledge of the mass, damping, and stiffness of the system—but can be measured experimentally. For example, if a known force over a range of frequencies is applied, and if the associated vibrations are measured, the frequency response function can be calculated, thereby characterizing the system. This technique is used in the field of experimental
 The simple mass–spring–damper model is the foundation of vibration analysis, but what about more complex systems? The mass–spring–damper model described above is called a single
The simple mass–spring–damper model is the foundation of vibration analysis, but what about more complex systems? The mass–spring–damper model described above is called a single
*
Whole-body and hand-arm vibration
* Manarikkal, I., Elsaha, F., Mba, D. and Laila, D. Dynamic Modelling of Planetary Gearboxes with Cracked Tooth Using Vibrational Analysis, (2019) Advances in Condition Monitoring of Machinery in Non-Stationary Operations, p 240-250, Springer, Switzerland
Free Excel sheets to estimate modal parametersVibration Analysis Reference – Mobius InstituteCondition Monitoring and Machinery Protection – Siemens AG
Mechanical vibrations, V
oscillation
Oscillation is the repetitive or periodic variation, typically in time, of some measure about a central value (often a point of equilibrium) or between two or more different states. Familiar examples of oscillation include a swinging pendulum ...
s occur about an equilibrium point
In mathematics, specifically in differential equations, an equilibrium point is a constant solution to a differential equation.
Formal definition
The point \tilde\in \mathbb^n is an equilibrium point for the differential equation
:\frac = \ ...
. The word comes from Latin ''vibrationem'' ("shaking, brandishing"). The oscillations may be periodic, such as the motion of a pendulum—or random
In common usage, randomness is the apparent or actual lack of pattern or predictability in events. A random sequence of events, symbols or steps often has no :wikt:order, order and does not follow an intelligible pattern or combination. Ind ...
, such as the movement of a tire on a gravel road.
Vibration can be desirable: for example, the motion of a tuning fork
A tuning fork is an acoustic resonator in the form of a two-pronged fork with the prongs (tines) formed from a U-shaped bar of elastic metal (usually steel). It resonates at a specific constant pitch when set vibrating by striking it against ...
, the reed
Reed or Reeds may refer to:
Science, technology, biology, and medicine
* Reed bird (disambiguation)
* Reed pen, writing implement in use since ancient times
* Reed (plant), one of several tall, grass-like wetland plants of the order Poales
* ...
in a woodwind instrument
Woodwind instruments are a family of musical instruments within the greater category of wind instruments. Common examples include flute, clarinet, oboe, bassoon, and saxophone. There are two main types of woodwind instruments: flutes and Reed ...
or harmonica
The harmonica, also known as a French harp or mouth organ, is a free reed wind instrument used worldwide in many musical genres, notably in blues, American folk music, classical music, jazz, country, and rock. The many types of harmonica inclu ...
, a mobile phone
A mobile phone, cellular phone, cell phone, cellphone, handphone, hand phone or pocket phone, sometimes shortened to simply mobile, cell, or just phone, is a portable telephone that can make and receive calls over a radio frequency link whil ...
, or the cone of a loudspeaker
A loudspeaker (commonly referred to as a speaker or speaker driver) is an electroacoustic transducer that converts an electrical audio signal into a corresponding sound. A ''speaker system'', also often simply referred to as a "speaker" or " ...
.
In many cases, however, vibration is undesirable, wasting energy
In physics, energy (from Ancient Greek: ἐνέργεια, ''enérgeia'', “activity”) is the quantitative property that is transferred to a body or to a physical system, recognizable in the performance of work and in the form of heat a ...
and creating unwanted sound
In physics, sound is a vibration that propagates as an acoustic wave, through a transmission medium such as a gas, liquid or solid.
In human physiology and psychology, sound is the ''reception'' of such waves and their ''perception'' by the ...
. For example, the vibrational motions of engine
An engine or motor is a machine designed to convert one or more forms of energy into mechanical energy.
Available energy sources include potential energy (e.g. energy of the Earth's gravitational field as exploited in hydroelectric power gen ...
s, electric motor
An electric motor is an Electric machine, electrical machine that converts electrical energy into mechanical energy. Most electric motors operate through the interaction between the motor's magnetic field and electric current in a Electromagneti ...
s, or any mechanical device
A machine is a physical system using power to apply forces and control movement to perform an action. The term is commonly applied to artificial devices, such as those employing engines or motors, but also to natural biological macromolecul ...
in operation are typically unwanted. Such vibrations could be caused by imbalances in the rotating parts, uneven friction
Friction is the force resisting the relative motion of solid surfaces, fluid layers, and material elements sliding against each other. There are several types of friction:
*Dry friction is a force that opposes the relative lateral motion of t ...
, or the meshing of gear
A gear is a rotating circular machine part having cut teeth or, in the case of a cogwheel or gearwheel, inserted teeth (called ''cogs''), which mesh with another (compatible) toothed part to transmit (convert) torque and speed. The basic pr ...
teeth. Careful designs usually minimize unwanted vibrations.
The studies of sound and vibration are closely related. Sound, or pressure wave
In physics, mathematics, and related fields, a wave is a propagating dynamic disturbance (change from equilibrium) of one or more quantities. Waves can be periodic, in which case those quantities oscillate repeatedly about an equilibrium (res ...
s, are generated by vibrating structures (e.g. vocal cords
In humans, vocal cords, also known as vocal folds or voice reeds, are folds of throat tissues that are key in creating sounds through vocalization. The size of vocal cords affects the pitch of voice. Open when breathing and vibrating for speech ...
); these pressure waves can also induce the vibration of structures (e.g. ear drum
In the anatomy of humans and various other tetrapods, the eardrum, also called the tympanic membrane or myringa, is a thin, cone-shaped membrane that separates the external ear from the middle ear. Its function is to transmit sound from the air ...
). Hence, attempts to reduce noise are often related to issues of vibration.


Machining vibrations
Machining vibrations, also called chatter, are the relative movement between the workpiece and the cutting tool. The vibrations result in waves on the machined surface. This affects typical machining processes, such as turning, milling and drilli ...
are common in the process of subtractive manufacturing
Machining is a process in which a material (often metal) is cut to a desired final shape and size by a controlled material-removal process. The processes that have this common theme are collectively called subtractive manufacturing, which utilizes ...
.
Types
Free vibration occurs when a mechanical system is set in motion with an initial input and allowed to vibrate freely. Examples of this type of vibration are pulling a child back on a swing and letting it go, or hitting a tuning fork and letting it ring. The mechanical system vibrates at one or more of itsnatural frequencies
The fundamental frequency, often referred to simply as the ''fundamental'', is defined as the lowest frequency of a periodic waveform. In music, the fundamental is the musical pitch of a note that is perceived as the lowest partial present. In ...
and damps
Damage-associated molecular patterns (DAMPs) are molecules within cells that are a component of the innate immune response released from damaged or dying cells due to trauma or an infection by a pathogen. They are also known as danger-associated ...
down to motionlessness.
Forced vibration is when a time-varying disturbance (load, displacement, velocity, or acceleration) is applied to a mechanical system. The disturbance can be a periodic and steady-state input, a transient input, or a random input. The periodic input can be a harmonic or a non-harmonic disturbance. Examples of these types of vibration include a washing machine shaking due to an imbalance, transportation vibration caused by an engine or uneven road, or the vibration of a building during an earthquake. For linear systems, the frequency of the steady-state vibration response resulting from the application of a periodic, harmonic input is equal to the frequency of the applied force or motion, with the response magnitude being dependent on the actual mechanical system.
Damped vibration: When the energy of a vibrating system is gradually dissipated by friction and other resistances, the vibrations are said to be damped. The vibrations gradually reduce or change in frequency or intensity or cease and the system rests in its equilibrium position. An example of this type of vibration is the vehicular suspension dampened by the shock absorber
A shock absorber or damper is a mechanical or hydraulic device designed to absorb and damp shock impulses. It does this by converting the kinetic energy of the shock into another form of energy (typically heat) which is then dissipated. Most sh ...
.
Isolation
Testing
Vibration testing is accomplished by introducing a forcing function into a structure, usually with some type of shaker. Alternately, a DUT (device under test) is attached to the "table" of a shaker. Vibration testing is performed to examine the response of a device under test (DUT) to a defined vibration environment. The measured response may be ability to function in the vibration environment, fatigue life, resonant frequencies or squeak and rattle sound output ( NVH). Squeak and rattle testing is performed with a special type of ''quiet shaker'' that produces very low sound levels while under operation. For relatively low frequency forcing (typically less than 100 Hz), servohydraulic (electrohydraulic) shakers are used. For higher frequencies (typically 5 Hz to 2000 Hz), electrodynamic shakers are used. Generally, one or more "input" or "control" points located on the DUT-side of a vibration fixture is kept at a specified acceleration.Tustin, Wayne.Where to place the control accelerometer: one of the most critical decisions in developing random vibration tests also is the most neglected
', EE-Evaluation Engineering, 2006 Other "response" points may experience higher vibration levels (resonance) or lower vibration level (anti-resonance or damping) than the control point(s). It is often desirable to achieve anti-resonance to keep a system from becoming too noisy, or to reduce strain on certain parts due to vibration modes caused by specific vibration frequencies. The most common types of vibration testing services conducted by vibration test labs are sinusoidal and random. Sine (one-frequency-at-a-time) tests are performed to survey the structural response of the device under test (DUT). During the early history of vibration testing, vibration machine controllers were limited only to controlling sine motion so only sine testing was performed. Later, more sophisticated analog and then digital controllers were able to provide random control (all frequencies at once). A random (all frequencies at once) test is generally considered to more closely replicate a real world environment, such as road inputs to a moving automobile. Most vibration testing is conducted in a 'single DUT axis' at a time, even though most real-world vibration occurs in various axes simultaneously. MIL-STD-810G, released in late 2008, Test Method 527, calls for multiple exciter testing. The ''vibration test fixtureTony Araujo.
The evolution of automotive vibration fixturing
', EE-Evaluation Engineering, 2019'' used to attach the DUT to the shaker table must be designed for the frequency range of the vibration test spectrum. It is difficult to design a vibration test fixture which duplicates the dynamic response (mechanical impedance)Blanks, H.S., "Equivalence Techniques for Vibration Testing," SVIC Notes, pp 17. of the actual in-use mounting. For this reason, to ensure repeatability between vibration tests, vibration fixtures are designed to be resonance free within the test frequency range. Generally for smaller fixtures and lower frequency ranges, the designer can target a fixture design that is free of resonances in the test frequency range. This becomes more difficult as the DUT gets larger and as the test frequency increases. In these cases multi-point control strategiesAraujo, T. and Yao, B., ''"Vibration Fixture Performance Qualification – A Review of Automotive Industry Best Practices," SAE Technical Paper 2020-01-1065, 2020, https://doi.org/10.4271/2020-01-1065.'' can mitigate some of the resonances that may be present in the future. Some vibration test methods limit the amount of crosstalk (movement of a response point in a mutually perpendicular direction to the axis under test) permitted to be exhibited by the vibration test fixture. Devices specifically designed to trace or record vibrations are called
vibroscope
Vibroscope ( la, vibrare 'vibrate' + scope) is an instrument for observing and tracing (and sometimes recording) vibration.
For example, a primitive mechanical vibroscope consists of a vibrating object with a pointy end which leaves a wave trace ...
s.
Analysis
Vibration analysis (VA), applied in an industrial or maintenance environment aims to reduce maintenance costs and equipment downtime by detecting equipment faults. VA is a key component of acondition monitoring
Condition monitoring (colloquially, CM) is the process of monitoring a parameter of condition in machinery (vibration, temperature etc.), in order to identify a significant change which is indicative of a developing fault. It is a major component o ...
(CM) program, and is often referred to as predictive maintenance
Predictive maintenance techniques are designed to help determine the condition of in-service equipment in order to estimate when maintenance should be performed. This approach promises cost savings over routine or time-based preventive maintena ...
(PdM). Most commonly VA is used to detect faults in rotating equipment (Fans, Motors, Pumps, and Gearboxes etc.) such as imbalance, misalignment, rolling element bearing faults and resonance conditions.
VA can use the units of Displacement, Velocity and Acceleration displayed as a time waveform (TWF), but most commonly the spectrum is used, derived from a fast Fourier transform of the TWF. The vibration spectrum provides important frequency information that can pinpoint the faulty component.
The fundamentals of vibration analysis can be understood by studying the simple Mass-spring-damper model. Indeed, even a complex structure such as an automobile body can be modeled as a "summation" of simple mass–spring–damper models. The mass–spring–damper model is an example of a simple harmonic oscillator
In mechanics and physics, simple harmonic motion (sometimes abbreviated ) is a special type of periodic motion of a body resulting from a dynamic equilibrium between an inertial force, proportional to the acceleration of the body away from the ...
. The mathematics used to describe its behavior is identical to other simple harmonic oscillators such as the RLC circuit
An RLC circuit is an electrical circuit consisting of a electrical resistance, resistor (R), an inductor (L), and a capacitor (C), connected in series or in parallel. The name of the circuit is derived from the letters that are used to denote the ...
.
Note: This article does not include the step-by-step mathematical derivations, but focuses on major vibration analysis equations and concepts. Please refer to the references at the end of the article for detailed derivations.
Free vibration without damping
Newton's second law of motion
Newton's laws of motion are three basic laws of classical mechanics that describe the relationship between the motion of an object and the forces acting on it. These laws can be paraphrased as follows:
# A body remains at rest, or in motion ...
:
:
The sum of the forces on the mass then generates this ordinary differential equation
In mathematics, an ordinary differential equation (ODE) is a differential equation whose unknown(s) consists of one (or more) function(s) of one variable and involves the derivatives of those functions. The term ''ordinary'' is used in contrast w ...
:
 Assuming that the initiation of vibration begins by stretching the spring by the distance of ''A'' and releasing, the solution to the above equation that describes the motion of mass is:
:
This solution says that it will oscillate with
Assuming that the initiation of vibration begins by stretching the spring by the distance of ''A'' and releasing, the solution to the above equation that describes the motion of mass is:
:
This solution says that it will oscillate with simple harmonic motion
In mechanics and physics, simple harmonic motion (sometimes abbreviated ) is a special type of periodic motion of a body resulting from a dynamic equilibrium between an inertial force, proportional to the acceleration of the body away from the ...
that has an amplitude
The amplitude of a periodic variable is a measure of its change in a single period (such as time or spatial period). The amplitude of a non-periodic signal is its magnitude compared with a reference value. There are various definitions of amplit ...
of ''A'' and a frequency of ''fn''. The number ''fn'' is called the undamped natural frequency. For the simple mass–spring system, ''fn'' is defined as:
:
Note: angular frequency
In physics, angular frequency "''ω''" (also referred to by the terms angular speed, circular frequency, orbital frequency, radian frequency, and pulsatance) is a scalar measure of rotation rate. It refers to the angular displacement per unit tim ...
ω (ω=2 π ''f'') with the units of radians per second is often used in equations because it simplifies the equations, but is normally converted to ordinary frequency
Frequency is the number of occurrences of a repeating event per unit of time. It is also occasionally referred to as ''temporal frequency'' for clarity, and is distinct from ''angular frequency''. Frequency is measured in hertz (Hz) which is eq ...
(units of Hz or equivalently cycles per second) when stating the frequency of a system. If the mass and stiffness of the system is known, the formula above can determine the frequency at which the system vibrates once set in motion by an initial disturbance. Every vibrating system has one or more natural frequencies that it vibrates at once disturbed. This simple relation can be used to understand in general what happens to a more complex system once we add mass or stiffness. For example, the above formula explains why, when a car or truck is fully loaded, the suspension feels ″softer″ than unloaded—the mass has increased, reducing the natural frequency of the system.
What causes the system to vibrate: from conservation of energy point of view
Vibrational motion could be understood in terms ofconservation of energy
In physics and chemistry, the law of conservation of energy states that the total energy of an isolated system remains constant; it is said to be ''conserved'' over time. This law, first proposed and tested by Émilie du Châtelet, means th ...
. In the above example the spring has been extended by a value of x and therefore some potential energy
In physics, potential energy is the energy held by an object because of its position relative to other objects, stresses within itself, its electric charge, or other factors.
Common types of potential energy include the gravitational potentia ...
() is stored in the spring. Once released, the spring tends to return to its un-stretched state (which is the minimum potential energy state) and in the process accelerates the mass. At the point where the spring has reached its un-stretched state all the potential energy that we supplied by stretching it has been transformed into kinetic energy
In physics, the kinetic energy of an object is the energy that it possesses due to its motion.
It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its accele ...
(). The mass then begins to decelerate because it is now compressing the spring and in the process transferring the kinetic energy back to its potential. Thus oscillation of the spring amounts to the transferring back and forth of the kinetic energy into potential energy. In this simple model the mass continues to oscillate forever at the same magnitude—but in a real system, ''damping'' always dissipates the energy, eventually bringing the spring to rest.
Free vibration with damping
overdamped
Damping is an influence within or upon an oscillatory system that has the effect of reducing or preventing its oscillation. In physical systems, damping is produced by processes that dissipate the energy stored in the oscillation. Examples incl ...
. The value that the damping coefficient must reach for critical damping in the mass-spring-damper model
The mass-spring-damper model consists of discrete mass nodes distributed throughout an object and interconnected via a network of springs and dampers. This model is well-suited for modelling object with complex material properties such as nonl ...
is:
:
To characterize the amount of damping in a system a ratio called the damping ratio
Damping is an influence within or upon an oscillatory system that has the effect of reducing or preventing its oscillation. In physical systems, damping is produced by processes that dissipate the energy stored in the oscillation. Examples inc ...
(also known as damping factor and % critical damping) is used. This damping ratio is just a ratio of the actual damping over the amount of damping required to reach critical damping. The formula for the damping ratio () of the mass-spring-damper model is:
:
For example, metal structures (e.g., airplane fuselages, engine crankshafts) have damping factors less than 0.05, while automotive suspensions are in the range of 0.2–0.3. The solution to the underdamped system
Damping is an influence within or upon an oscillatory system that has the effect of reducing or preventing its oscillation. In physical systems, damping is produced by processes that dissipate the energy stored in the oscillation. Examples inc ...
for the mass-spring-damper model is the following:
:
 The value of ''X'', the initial magnitude, and the
The value of ''X'', the initial magnitude, and the phase shift
In physics and mathematics, the phase of a periodic function F of some real variable t (such as time) is an angle-like quantity representing the fraction of the cycle covered up to t. It is denoted \phi(t) and expressed in such a scale that it v ...
, are determined by the amount the spring is stretched. The formulas for these values can be found in the references.
Damped and undamped natural frequencies
The major points to note from the solution are the exponential term and the cosine function. The exponential term defines how quickly the system “damps” down – the larger the damping ratio, the quicker it damps to zero. The cosine function is the oscillating portion of the solution, but the frequency of the oscillations is different from the undamped case. The frequency in this case is called the "damped natural frequency", and is related to the undamped natural frequency by the following formula: : The damped natural frequency is less than the undamped natural frequency, but for many practical cases the damping ratio is relatively small and hence the difference is negligible. Therefore, the damped and undamped description are often dropped when stating the natural frequency (e.g. with 0.1 damping ratio, the damped natural frequency is only 1% less than the undamped). The plots to the side present how 0.1 and 0.3 damping ratios effect how the system “rings” down over time. What is often done in practice is to experimentally measure the free vibration after an impact (for example by a hammer) and then determine the natural frequency of the system by measuring the rate of oscillation, as well as the damping ratio by measuring the rate of decay. The natural frequency and damping ratio are not only important in free vibration, but also characterize how a system behaves under forced vibration.Forced vibration with damping
The behavior of the spring mass damper model varies with the addition of a harmonic force. A force of this type could, for example, be generated by a rotating imbalance. : Summing the forces on the mass results in the following ordinary differential equation: : Thesteady state
In systems theory, a system or a Process theory, process is in a steady state if the variables (called state variables) which define the behavior of the system or the process are unchanging in time. In continuous time, this means that for those p ...
solution of this problem can be written as:
:
The result states that the mass will oscillate at the same frequency, ''f'', of the applied force, but with a phase shift
The amplitude of the vibration “X” is defined by the following formula.
:
Where “r” is defined as the ratio of the harmonic force frequency over the undamped natural frequency of the mass–spring–damper model.
:
The phase shift, is defined by the following formula.
:
 The plot of these functions, called "the frequency response of the system", presents one of the most important features in forced vibration. In a lightly damped system when the forcing frequency nears the natural frequency () the amplitude of the vibration can get extremely high. This phenomenon is called
The plot of these functions, called "the frequency response of the system", presents one of the most important features in forced vibration. In a lightly damped system when the forcing frequency nears the natural frequency () the amplitude of the vibration can get extremely high. This phenomenon is called resonance
Resonance describes the phenomenon of increased amplitude that occurs when the frequency of an applied periodic force (or a Fourier component of it) is equal or close to a natural frequency of the system on which it acts. When an oscillatin ...
(subsequently the natural frequency of a system is often referred to as the resonant frequency). In rotor bearing systems any rotational speed that excites a resonant frequency is referred to as a critical speed In solid mechanics, in the field of rotordynamics, the critical speed is the theoretical angular velocity that excites the natural frequency of a rotating object, such as a shaft, propeller, leadscrew, or gear. As the speed of rotation approache ...
.
If resonance occurs in a mechanical system it can be very harmful – leading to eventual failure of the system. Consequently, one of the major reasons for vibration analysis is to predict when this type of resonance may occur and then to determine what steps to take to prevent it from occurring. As the amplitude plot shows, adding damping can significantly reduce the magnitude of the vibration. Also, the magnitude can be reduced if the natural frequency can be shifted away from the forcing frequency by changing the stiffness or mass of the system. If the system cannot be changed, perhaps the forcing frequency can be shifted (for example, changing the speed of the machine generating the force).
The following are some other points in regards to the forced vibration shown in the frequency response plots.
*At a given frequency ratio, the amplitude of the vibration, ''X'', is directly proportional to the amplitude of the force (e.g. if you double the force, the vibration doubles)
*With little or no damping, the vibration is in phase with the forcing frequency when the frequency ratio ''r'' < 1 and 180 degrees out of phase when the frequency ratio ''r'' > 1
*When ''r'' ≪ 1 the amplitude is just the deflection of the spring under the static force This deflection is called the static deflection Hence, when ''r'' ≪ 1 the effects of the damper and the mass are minimal.
*When ''r'' ≫ 1 the amplitude of the vibration is actually less than the static deflection In this region the force generated by the mass (''F'' = ''ma'') is dominating because the acceleration seen by the mass increases with the frequency. Since the deflection seen in the spring, ''X'', is reduced in this region, the force transmitted by the spring (''F'' = ''kx'') to the base is reduced. Therefore, the mass–spring–damper system is isolating the harmonic force from the mounting base – referred to as vibration isolation Vibration isolation is the process of isolating an object, such as a piece of equipment, from the source of vibrations.
Vibration is undesirable in many domains, primarily engineered systems and habitable spaces, and methods have been developed to p ...
. More damping actually reduces the effects of vibration isolation when ''r'' ≫ 1 because the damping force (''F'' = ''cv'') is also transmitted to the base.
* Whatever the damping is, the vibration is 90 degrees out of phase with the forcing frequency when the frequency ratio ''r'' = 1, which is very helpful when it comes to determining the natural frequency of the system.
* Whatever the damping is, when ''r'' ≫ 1, the vibration is 180 degrees out of phase with the forcing frequency
* Whatever the damping is, when ''r'' ≪ 1, the vibration is in phase with the forcing frequency
Resonance causes
Resonance is simple to understand if the spring and mass are viewed as energy storage elements – with the mass storing kinetic energy and the spring storing potential energy. As discussed earlier, when the mass and spring have no external force acting on them they transfer energy back and forth at a rate equal to the natural frequency. In other words, to efficiently pump energy into both mass and spring requires that the energy source feed the energy in at a rate equal to the natural frequency. Applying a force to the mass and spring is similar to pushing a child on swing, a push is needed at the correct moment to make the swing get higher and higher. As in the case of the swing, the force applied need not be high to get large motions, but must just add energy to the system. The damper, instead of storing energy, dissipates energy. Since the damping force is proportional to the velocity, the more the motion, the more the damper dissipates the energy. Therefore, there is a point when the energy dissipated by the damper equals the energy added by the force. At this point, the system has reached its maximum amplitude and will continue to vibrate at this level as long as the force applied stays the same. If no damping exists, there is nothing to dissipate the energy and, theoretically, the motion will continue to grow into infinity.Applying "complex" forces to the mass–spring–damper model
In a previous section only a simple harmonic force was applied to the model, but this can be extended considerably using two powerful mathematical tools. The first is theFourier transform
A Fourier transform (FT) is a mathematical transform that decomposes functions into frequency components, which are represented by the output of the transform as a function of frequency. Most commonly functions of time or space are transformed, ...
that takes a signal as a function of time (time domain
Time domain refers to the analysis of mathematical functions, physical signals or time series of economic or environmental data, with respect to time. In the time domain, the signal or function's value is known for all real numbers, for the cas ...
) and breaks it down into its harmonic components as a function of frequency (frequency domain
In physics, electronics, control systems engineering, and statistics, the frequency domain refers to the analysis of mathematical functions or signals with respect to frequency, rather than time. Put simply, a time-domain graph shows how a signa ...
). For example, by applying a force to the mass–spring–damper model that repeats the following cycle – a force equal to 1 newton
Newton most commonly refers to:
* Isaac Newton (1642–1726/1727), English scientist
* Newton (unit), SI unit of force named after Isaac Newton
Newton may also refer to:
Arts and entertainment
* ''Newton'' (film), a 2017 Indian film
* Newton ( ...
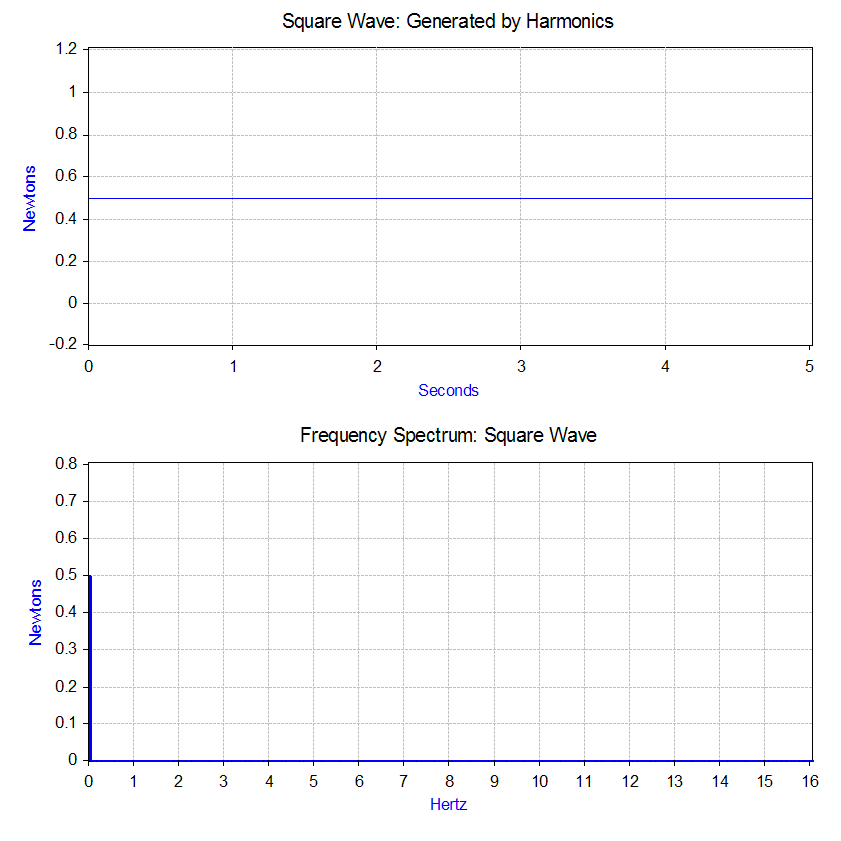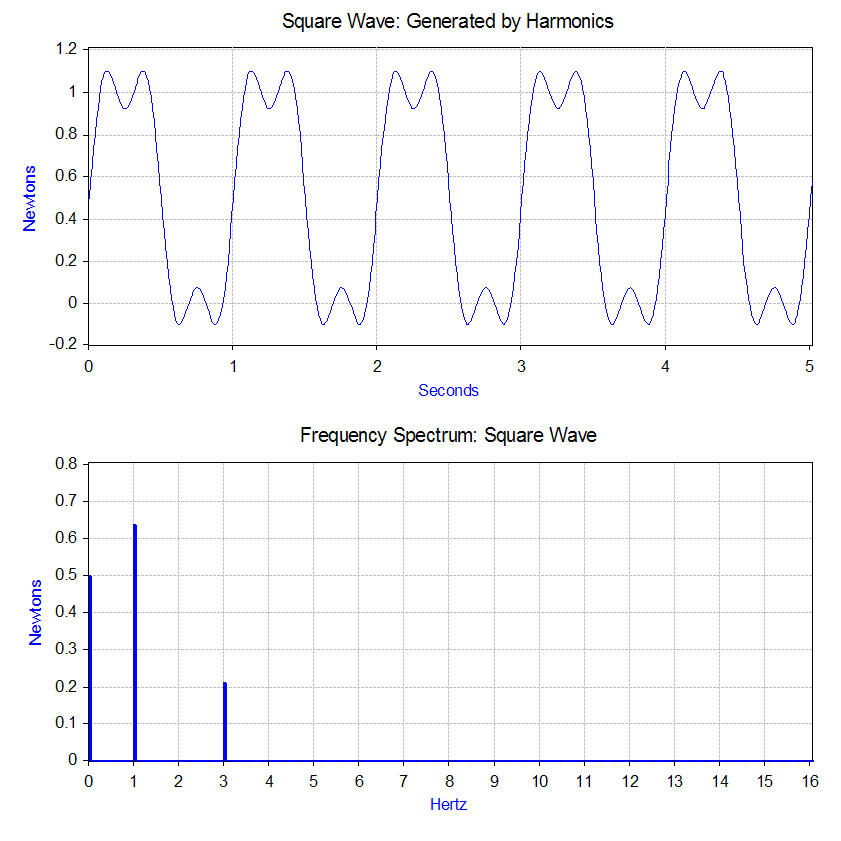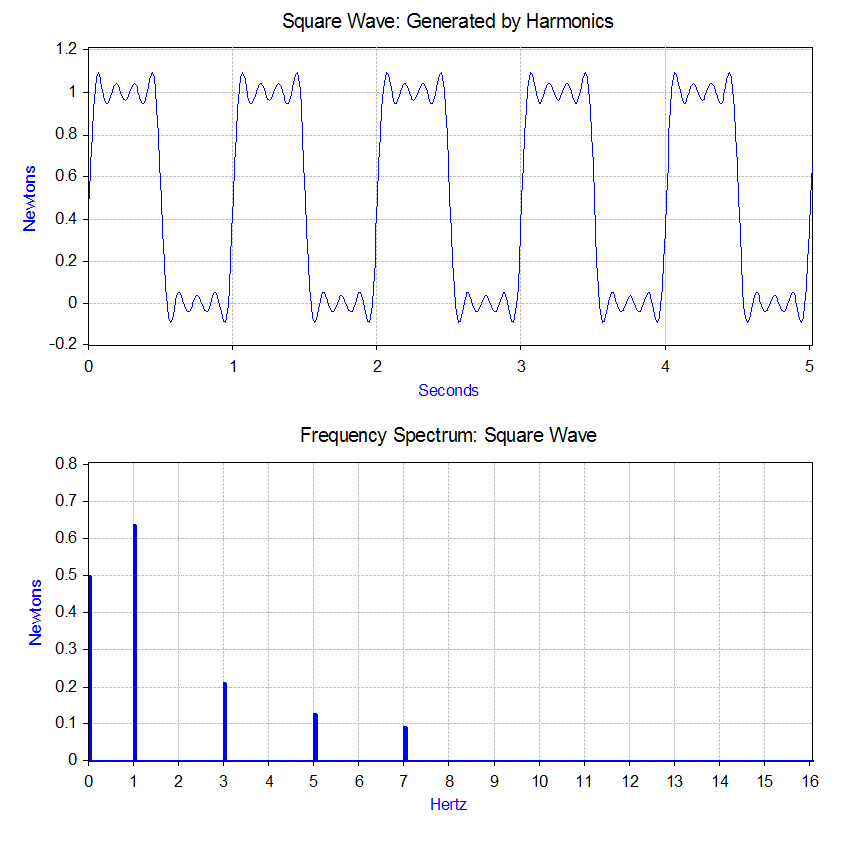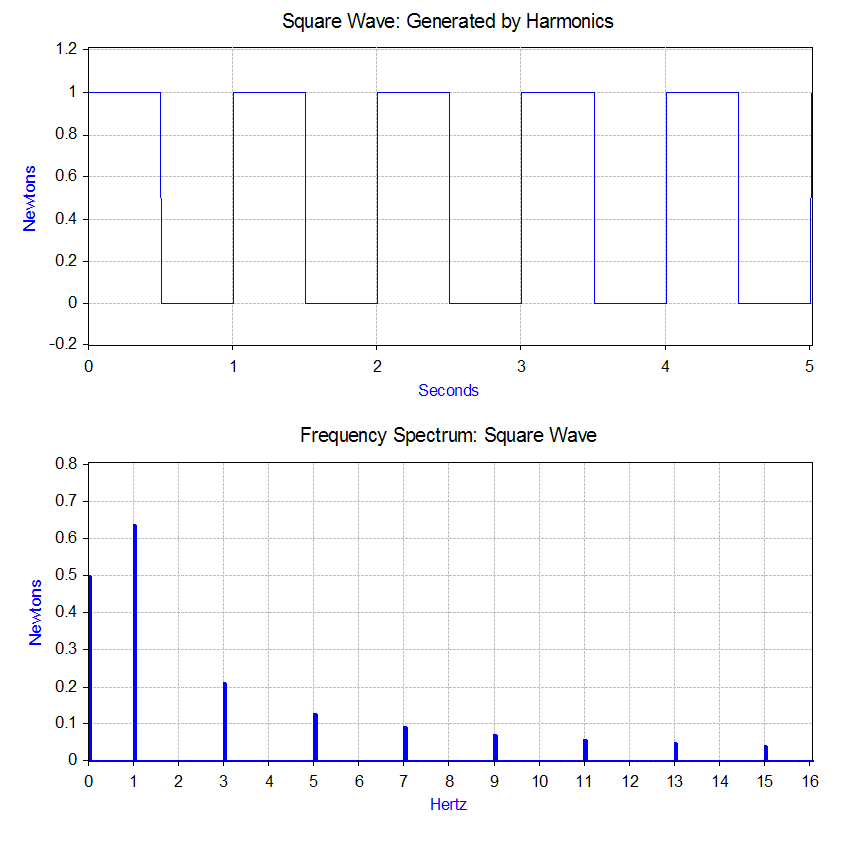
for 0.5 second and then no force for 0.5 second. This type of force has the shape of a 1 Hz square wave
A square wave is a non-sinusoidal periodic waveform in which the amplitude alternates at a steady frequency between fixed minimum and maximum values, with the same duration at minimum and maximum. In an ideal square wave, the transitions b ...
.
 The Fourier transform of the square wave generates a
The Fourier transform of the square wave generates a frequency spectrum
The power spectrum S_(f) of a time series x(t) describes the distribution of power into frequency components composing that signal. According to Fourier analysis, any physical signal can be decomposed into a number of discrete frequencies, ...
that presents the magnitude of the harmonics that make up the square wave (the phase is also generated, but is typically of less concern and therefore is often not plotted). The Fourier transform can also be used to analyze non- periodic functions such as transients (e.g. impulses) and random functions. The Fourier transform is almost always computed using the fast Fourier transform (FFT) computer algorithm in combination with a window function
In signal processing and statistics, a window function (also known as an apodization function or tapering function) is a mathematical function that is zero-valued outside of some chosen interval, normally symmetric around the middle of the inte ...
.
In the case of our square wave force, the first component is actually a constant force of 0.5 newton and is represented by a value at 0 Hz in the frequency spectrum. The next component is a 1 Hz sine wave with an amplitude of 0.64. This is shown by the line at 1 Hz. The remaining components are at odd frequencies and it takes an infinite amount of sine waves to generate the perfect square wave. Hence, the Fourier transform allows you to interpret the force as a sum of sinusoidal forces being applied instead of a more "complex" force (e.g. a square wave).
In the previous section, the vibration solution was given for a single harmonic force, but the Fourier transform in general gives multiple harmonic forces. The second mathematical tool, the superposition principle
The superposition principle, also known as superposition property, states that, for all linear systems, the net response caused by two or more stimuli is the sum of the responses that would have been caused by each stimulus individually. So tha ...
, allows the summation of the solutions from multiple forces if the system is linear
Linearity is the property of a mathematical relationship (''function'') that can be graphically represented as a straight line. Linearity is closely related to '' proportionality''. Examples in physics include rectilinear motion, the linear r ...
. In the case of the spring–mass–damper model, the system is linear if the spring force is proportional to the displacement and the damping is proportional to the velocity over the range of motion of interest. Hence, the solution to the problem with a square wave is summing the predicted vibration from each one of the harmonic forces found in the frequency spectrum of the square wave.
Frequency response model
The solution of a vibration problem can be viewed as an input/output relation – where the force is the input and the output is the vibration. Representing the force and vibration in the frequency domain (magnitude and phase) allows the following relation: : is called thefrequency response
In signal processing and electronics, the frequency response of a system is the quantitative measure of the magnitude and phase of the output as a function of input frequency. The frequency response is widely used in the design and analysis of sy ...
function (also referred to as the transfer function
In engineering, a transfer function (also known as system function or network function) of a system, sub-system, or component is a function (mathematics), mathematical function that mathematical model, theoretically models the system's output for ...
, but not technically as accurate) and has both a magnitude and phase component (if represented as a complex number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the form ...
, a real and imaginary component). The magnitude of the frequency response function (FRF) was presented earlier for the mass–spring–damper system.
:
The phase of the FRF was also presented earlier as:
:
 For example, calculating the FRF for a mass–spring–damper system with a mass of 1 kg, spring stiffness of 1.93 N/mm and a damping ratio of 0.1. The values of the spring and mass give a natural frequency of 7 Hz for this specific system. Applying the 1 Hz square wave from earlier allows the calculation of the predicted vibration of the mass. The figure illustrates the resulting vibration. It happens in this example that the fourth harmonic of the square wave falls at 7 Hz. The frequency response of the mass–spring–damper therefore outputs a high 7 Hz vibration even though the input force had a relatively low 7 Hz harmonic. This example highlights that the resulting vibration is dependent on both the forcing function and the system that the force is applied to.
The figure also shows the time domain representation of the resulting vibration. This is done by performing an inverse Fourier Transform that converts frequency domain data to time domain. In practice, this is rarely done because the frequency spectrum provides all the necessary information.
The frequency response function (FRF) does not necessarily have to be calculated from the knowledge of the mass, damping, and stiffness of the system—but can be measured experimentally. For example, if a known force over a range of frequencies is applied, and if the associated vibrations are measured, the frequency response function can be calculated, thereby characterizing the system. This technique is used in the field of experimental
For example, calculating the FRF for a mass–spring–damper system with a mass of 1 kg, spring stiffness of 1.93 N/mm and a damping ratio of 0.1. The values of the spring and mass give a natural frequency of 7 Hz for this specific system. Applying the 1 Hz square wave from earlier allows the calculation of the predicted vibration of the mass. The figure illustrates the resulting vibration. It happens in this example that the fourth harmonic of the square wave falls at 7 Hz. The frequency response of the mass–spring–damper therefore outputs a high 7 Hz vibration even though the input force had a relatively low 7 Hz harmonic. This example highlights that the resulting vibration is dependent on both the forcing function and the system that the force is applied to.
The figure also shows the time domain representation of the resulting vibration. This is done by performing an inverse Fourier Transform that converts frequency domain data to time domain. In practice, this is rarely done because the frequency spectrum provides all the necessary information.
The frequency response function (FRF) does not necessarily have to be calculated from the knowledge of the mass, damping, and stiffness of the system—but can be measured experimentally. For example, if a known force over a range of frequencies is applied, and if the associated vibrations are measured, the frequency response function can be calculated, thereby characterizing the system. This technique is used in the field of experimental modal analysis
Modal analysis is the study of the dynamic properties of systems in the frequency domain. Examples would include measuring the vibration of a car's body when it is attached to a shaker, or the noise pattern in a room when excited by a loudspeak ...
to determine the vibration characteristics of a structure.
Multiple degrees of freedom systems and mode shapes
 The simple mass–spring–damper model is the foundation of vibration analysis, but what about more complex systems? The mass–spring–damper model described above is called a single
The simple mass–spring–damper model is the foundation of vibration analysis, but what about more complex systems? The mass–spring–damper model described above is called a single degree of freedom
Degrees of freedom (often abbreviated df or DOF) refers to the number of independent variables or parameters of a thermodynamic system. In various scientific fields, the word "freedom" is used to describe the limits to which physical movement or ...
(SDOF) model since the mass is assumed to only move up and down. In more complex systems, the system must be discretized into more masses that move in more than one direction, adding degrees of freedom. The major concepts of multiple degrees of freedom (MDOF) can be understood by looking at just a 2 degree of freedom model as shown in the figure.
The equations of motion of the 2DOF system are found to be:
:
:
This can be rewritten in matrix
Matrix most commonly refers to:
* ''The Matrix'' (franchise), an American media franchise
** ''The Matrix'', a 1999 science-fiction action film
** "The Matrix", a fictional setting, a virtual reality environment, within ''The Matrix'' (franchis ...
format:
:
A more compact form of this matrix equation can be written as:
:
where and are symmetric matrices
In linear algebra, a symmetric matrix is a square matrix that is equal to its transpose. Formally,
Because equal matrices have equal dimensions, only square matrices can be symmetric.
The entries of a symmetric matrix are symmetric with re ...
referred respectively as the mass, damping, and stiffness matrices. The matrices are NxN square matrices where N is the number of degrees of freedom of the system.
The following analysis involves the case where there is no damping and no applied forces (i.e. free vibration). The solution of a viscously damped system is somewhat more complicated.Maia, Silva. ''Theoretical And Experimental Modal Analysis'', Research Studies Press Ltd., 1997,
:
This differential equation can be solved by assuming the following type of solution:
:
Note: Using the exponential solution of is a mathematical trick used to solve linear differential equations. Using Euler's formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the fundamental relationship between the trigonometric functions and the complex exponential function. Euler's formula states that for an ...
and taking only the real part of the solution it is the same cosine solution for the 1 DOF system. The exponential solution is only used because it is easier to manipulate mathematically.
The equation then becomes:
:
Since cannot equal zero the equation reduces to the following.
:
Eigenvalue problem
This is referred to aneigenvalue
In linear algebra, an eigenvector () or characteristic vector of a linear transformation is a nonzero vector that changes at most by a scalar factor when that linear transformation is applied to it. The corresponding eigenvalue, often denoted b ...
problem in mathematics and can be put in the standard format by pre-multiplying the equation by
:
and if: and
:
The solution to the problem results in N eigenvalues (i.e. ), where N corresponds to the number of degrees of freedom. The eigenvalues provide the natural frequencies of the system. When these eigenvalues are substituted back into the original set of equations, the values of that correspond to each eigenvalue are called the eigenvectors. These eigenvectors represent the mode shape
A normal mode of a dynamical system is a pattern of motion in which all parts of the system move sinusoidally with the same frequency and with a fixed phase relation. The free motion described by the normal modes takes place at fixed frequencies. ...
s of the system. The solution of an eigenvalue problem can be quite cumbersome (especially for problems with many degrees of freedom), but fortunately most math analysis programs have eigenvalue routines.
The eigenvalues and eigenvectors are often written in the following matrix format and describe the modal model of the system:
:
A simple example using the 2 DOF model can help illustrate the concepts. Let both masses have a mass of 1 kg and the stiffness of all three springs equal 1000 N/m. The mass and stiffness matrix for this problem are then:
: and
Then
The eigenvalues for this problem given by an eigenvalue routine is:
:
The natural frequencies in the units of hertz are then (remembering ) and
The two mode shapes for the respective natural frequencies are given as:
:
Since the system is a 2 DOF system, there are two modes with their respective natural frequencies and shapes. The mode shape vectors are not the absolute motion, but just describe relative motion of the degrees of freedom. In our case the first mode shape vector is saying that the masses are moving together in phase since they have the same value and sign. In the case of the second mode shape vector, each mass is moving in opposite direction at the same rate.
Illustration of a multiple DOF problem
When there are many degrees of freedom, one method of visualizing the mode shapes is by animating them using structural analysis software such asFemap
Femap (''Finite Element Modeling And Postprocessing'') is an engineering analysis program sold by Siemens Digital Industries Software that is used to build finite element models of complex engineering problems ("pre-processing") and view solution ...
, ANSYS or VA One by ESI Group
ESI Group provides virtual prototyping software that simulates a product's behavior during testing, manufacturing and real-life use. Engineers in a variety of industries use its software to evaluate the performance of proposed designs in the earl ...
. An example of animating mode shapes is shown in the figure below for a cantilever
A cantilever is a rigid structural element that extends horizontally and is supported at only one end. Typically it extends from a flat vertical surface such as a wall, to which it must be firmly attached. Like other structural elements, a canti ...
ed -beam as demonstrated using modal analysis
Modal analysis is the study of the dynamic properties of systems in the frequency domain. Examples would include measuring the vibration of a car's body when it is attached to a shaker, or the noise pattern in a room when excited by a loudspeak ...
on ANSYS. In this case, the finite element method
The finite element method (FEM) is a popular method for numerically solving differential equations arising in engineering and mathematical modeling. Typical problem areas of interest include the traditional fields of structural analysis, heat ...
was used to generate an approximation of the mass and stiffness matrices by meshing the object of interest in order to solve a discrete eigenvalue problem. Note that, in this case, the finite element method provides an approximation of the meshed surface (for which there exists an infinite number of vibration modes and frequencies). Therefore, this relatively simple model that has over 100 degrees of freedom and hence as many natural frequencies and mode shapes, provides a good approximation for the first natural frequencies and modes. Generally, only the first few modes are important for practical applications.
Note that when performing a numerical approximation of any mathematical model, convergence of the parameters of interest must be ascertained.
Multiple DOF problem converted to a single DOF problem
The eigenvectors have very important properties called orthogonality properties. These properties can be used to greatly simplify the solution of multi-degree of freedom models. It can be shown that the eigenvectors have the following properties: : : and arediagonal matrices
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero; the term usually refers to square matrices. Elements of the main diagonal can either be zero or nonzero. An example of a 2×2 diagonal m ...
that contain the modal mass and stiffness values for each one of the modes. (Note: Since the eigenvectors (mode shapes) can be arbitrarily scaled, the orthogonality properties are often used to scale the eigenvectors so the modal mass value for each mode is equal to 1. The modal mass matrix is therefore an identity matrix
In linear algebra, the identity matrix of size n is the n\times n square matrix with ones on the main diagonal and zeros elsewhere.
Terminology and notation
The identity matrix is often denoted by I_n, or simply by I if the size is immaterial o ...
)
These properties can be used to greatly simplify the solution of multi-degree of freedom models by making the following coordinate transformation.
:
Using this coordinate transformation in the original free vibration differential equation results in the following equation.
:
Taking advantage of the orthogonality properties by premultiplying this equation by
:
The orthogonality properties then simplify this equation to:
:
This equation is the foundation of vibration analysis for multiple degree of freedom systems. A similar type of result can be derived for damped systems. The key is that the modal mass and stiffness matrices are diagonal matrices and therefore the equations have been "decoupled". In other words, the problem has been transformed from a large unwieldy multiple degree of freedom problem into many single degree of freedom problems that can be solved using the same methods outlined above.
Solving for ''x'' is replaced by solving for ''q'', referred to as the modal coordinates or modal participation factors.
It may be clearer to understand if is written as:
:
Written in this form it can be seen that the vibration at each of the degrees of freedom is just a linear sum of the mode shapes. Furthermore, how much each mode "participates" in the final vibration is defined by q, its modal participation factor.
Rigid-body mode
An unrestrained multi-degree of freedom system experiences both rigid-body translation and/or rotation and vibration. The existence of a rigid-body mode results in a zero natural frequency. The corresponding mode shape is called the rigid-body mode.See also
*Acoustic engineering
Acoustical engineering (also known as acoustic engineering) is the branch of engineering dealing with sound and vibration. It includes the application of acoustics, the science of sound and vibration, in technology. Acoustical engineers are typical ...
*Anti-vibration compound
An anti-vibration compound is a temperature-resistant mixture of a liquid with fine particles, which is used to reduce oscillations in calender rolls
and to dampen vibrations in fabricated structures like machine beds and housings.
Use
Vibration ...
*Balancing machine
A balancing machine is a measuring tool used for balancing rotating machine parts such as rotors for electric motors, fans, turbines, disc brakes, disc drives, propellers and pumps. The machine usually consists of two rigid pedestals, with suspe ...
*Base isolation
Seismic base isolation, also known as base isolation, or base isolation system, is one of the most popular means of protecting a structure against earthquake forces. It is a collection of structural elements which should substantially decoupl ...
*Cushioning
Package cushioning is used to protect items during shipment. Vibration and impact shock during shipment and loading/unloading are controlled by cushioning to reduce the chance of product damage.
Cushioning is usually inside a shipping container ...
*Critical speed In solid mechanics, in the field of rotordynamics, the critical speed is the theoretical angular velocity that excites the natural frequency of a rotating object, such as a shaft, propeller, leadscrew, or gear. As the speed of rotation approache ...
*Damping ratio
Damping is an influence within or upon an oscillatory system that has the effect of reducing or preventing its oscillation. In physical systems, damping is produced by processes that dissipate the energy stored in the oscillation. Examples inc ...
*Dunkerley's method
Dunkerley's method is used in mechanical engineering to determine the critical speed of a shaft-rotor system. Other methods include the Rayleigh–Ritz method.
Whirling of a shaft
No shaft can ever be perfectly straight or perfectly balance ...
* Earthquake engineering
*Elastic pendulum
In physics and mathematics, in the area of dynamical systems, an elastic pendulum (also called spring pendulum or swinging spring) is a physical system where a piece of mass is connected to a spring so that the resulting motion contains elemen ...
* Fast Fourier transform
*Mechanical engineering
Mechanical engineering is the study of physical machines that may involve force and movement. It is an engineering branch that combines engineering physics and mathematics principles with materials science, to design, analyze, manufacture, and ...
*Mechanical resonance
Mechanical resonance is the tendency of a mechanical system to respond at greater amplitude when the frequency of its oscillations matches the system's natural frequency of vibration (its ''resonance frequency'' or ''resonant frequency'') close ...
*Modal analysis
Modal analysis is the study of the dynamic properties of systems in the frequency domain. Examples would include measuring the vibration of a car's body when it is attached to a shaker, or the noise pattern in a room when excited by a loudspeak ...
*Mode shape
A normal mode of a dynamical system is a pattern of motion in which all parts of the system move sinusoidally with the same frequency and with a fixed phase relation. The free motion described by the normal modes takes place at fixed frequencies. ...
*Noise and vibration on maritime vessels
Noise and vibration on maritime vessels are not the same but they have the same origin and come in many forms. The methods to handle the related problems are similar, to a certain level, where most shipboard noise problems are reduced by controllin ...
*Noise, vibration, and harshness
Noise, vibration, and harshness (NVH), also known as noise and vibration (N&V), is the study and modification of the noise and vibration characteristics of vehicles, particularly cars and trucks. While noise and vibration can be readily measured, ...
*Pallesthesia
Pallesthesia (\ˌpal-es-ˈthē-zh(ē-)ə\), or vibratory sensation, is the ability to perceive vibration.Campbell, W. W., & DeJong, R. N. (2013). DeJong's the neurologic examination. lectronic resourceWilliam W. Campbell. Philadelphia, PA : Lippi ...
*Passive heave compensation
Passive heave compensation is a technique used to reduce the influence of waves upon lifting and drilling operations. A simple passive heave compensator (PHC) is a soft spring which utilizes spring isolation to reduce transmissibility to less th ...
*Pendulum
A pendulum is a weight suspended from a pivot so that it can swing freely. When a pendulum is displaced sideways from its resting, equilibrium position, it is subject to a restoring force due to gravity that will accelerate it back toward the ...
*Quantum vibration
量子調和振動子 は、 古典調和振動子 の 量子力学 類似物です。任意の滑らかな ポテンシャル は通常、安定した 平衡点 の近くで 調和ポテンシャル として近似できるため、最� ...
*Random vibration In mechanical engineering, random vibration is motion which is non-deterministic, meaning that future behavior cannot be precisely predicted. The randomness is a characteristic of the excitation or input, not the mode shapes or natural frequencies. ...
*Ride quality
Ride quality refers to a vehicle's effectiveness in insulating the occupants from undulations in the road surface (e.g., bumps or corrugations).
A vehicle with good ride quality provides a comfort for the driver and passengers.
Importance
Good r ...
* Rayleigh's quotient in vibrations analysis
*Shaker (testing device)
A shaker is a device used in vibration testing to excite the structure, either for endurance testing or modal testing.
References
*Tongue, Benson, ''Principles of Vibration'', Oxford University Press, 2001,
*Inman, Daniel J., ''Engineering Vib ...
*Shock
Shock may refer to:
Common uses Collective noun
*Shock, a historic commercial term for a group of 60, see English numerals#Special names
* Stook, or shock of grain, stacked sheaves
Healthcare
* Shock (circulatory), circulatory medical emergen ...
* Shock and vibration data logger
*Simple harmonic oscillator
In mechanics and physics, simple harmonic motion (sometimes abbreviated ) is a special type of periodic motion of a body resulting from a dynamic equilibrium between an inertial force, proportional to the acceleration of the body away from the ...
*Sound
In physics, sound is a vibration that propagates as an acoustic wave, through a transmission medium such as a gas, liquid or solid.
In human physiology and psychology, sound is the ''reception'' of such waves and their ''perception'' by the ...
*Structural acoustics Structural acoustics is the study of the mechanical waves in structures and how they interact with and radiate into adjacent media. The field of structural acoustics is often referred to as vibroacoustics in Europe and Asia. People that work in th ...
*Structural dynamics
Structural dynamics is a type of structural analysis which covers the behavior of a structure subjected to dynamic (actions having high acceleration) loading. Dynamic loads include people, wind, waves, traffic, earthquakes, and blasts. Any structur ...
*Tire balance
Tire balance, also called tire unbalance or tire imbalance, describes the distribution of mass within an automobile tire or the entire wheel (including the rim) on which it is mounted.
When the wheel rotates, asymmetries in its mass distribution ...
* Torsional vibration
*Tuned mass damper
A tuned mass damper (TMD), also known as a harmonic absorber or seismic damper, is a device mounted in structures to reduce mechanical vibrations, consisting of a mass mounted on one or more damped springs. Its oscillation frequency is tuned ...
*Vibration calibrator
Vibration calibrators , sometimes also called reference shakers, are electromechanical instruments which enable calibration of vibration sensors and measuring instruments to traceable standards. They produce sinusoidal mechanical vibration signa ...
*Vibration control
In earthquake engineering, vibration control is a set of technical means aimed to mitigate seismic impacts in building and non-building structures.
All seismic vibration control devices may be classified as ''passive'', ''active'' or ''hybrid'' ...
*Vibration isolation Vibration isolation is the process of isolating an object, such as a piece of equipment, from the source of vibrations.
Vibration is undesirable in many domains, primarily engineered systems and habitable spaces, and methods have been developed to p ...
*Wave
In physics, mathematics, and related fields, a wave is a propagating dynamic disturbance (change from equilibrium) of one or more quantities. Waves can be periodic, in which case those quantities oscillate repeatedly about an equilibrium (res ...
*Whole body vibration
Whole body vibration is a generic term used when vibrations (mechanical oscillations) of any frequency are transferred to the human body. Humans are exposed to vibration through a contact surface that is in a mechanical vibrating state. Humans are ...
References
Further reading
*Tongue, Benson, ''Principles of Vibration'', Oxford University Press, 2001, *Inman, Daniel J., ''Engineering Vibration'', Prentice Hall, 2001, *Thompson, W.T., ''Theory of Vibrations'', Nelson Thornes Ltd, 1996, *Hartog, Den, ''Mechanical Vibrations'', Dover Publications, 1985, **
Institute for Occupational Safety and Health of the German Social Accident Insurance
The Institute for Occupational Safety and Health of the German Social Accident Insurance (German: ''Institut für Arbeitsschutz der Deutschen Gesetzlichen Unfallversicherung'', ''IFA'') is a German institute located in Sankt Augustin near Bonn and ...
Whole-body and hand-arm vibration
* Manarikkal, I., Elsaha, F., Mba, D. and Laila, D. Dynamic Modelling of Planetary Gearboxes with Cracked Tooth Using Vibrational Analysis, (2019) Advances in Condition Monitoring of Machinery in Non-Stationary Operations, p 240-250, Springer, Switzerland
External links
{{wikidata property, P2806Free Excel sheets to estimate modal parameters
Mechanical vibrations, V