|
Critical Speed
In solid mechanics, in the field of rotordynamics, the critical speed is the theoretical angular velocity that excites the natural frequency of a rotating object, such as a shaft, propeller, leadscrew, or gear. As the speed of rotation approaches the object's natural frequency, the object begins to resonate, which dramatically increases system vibration. The resulting resonance occurs regardless of orientation. When the rotational speed is equal to the numerical value of the natural vibration, then that speed is referred to as critical speed. Critical speed of shafts All rotating shafts, even in the absence of external load, will deflect during rotation. The unbalanced mass of the rotating object causes deflection that will create resonant vibration at certain speeds, known as the critical speeds. The magnitude of deflection depends upon the following: *Stiffness of the shaft and its support *Total mass of shaft and attached parts *Unbalance of the mass with respect to the axis of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Solid Mechanics
Solid mechanics, also known as mechanics of solids, is the branch of continuum mechanics that studies the behavior of solid materials, especially their motion and deformation under the action of forces, temperature changes, phase changes, and other external or internal agents. Solid mechanics is fundamental for civil, aerospace, nuclear, biomedical and mechanical engineering, for geology, and for many branches of physics such as materials science. It has specific applications in many other areas, such as understanding the anatomy of living beings, and the design of dental prostheses and surgical implants. One of the most common practical applications of solid mechanics is the Euler–Bernoulli beam equation. Solid mechanics extensively uses tensors to describe stresses, strains, and the relationship between them. Solid mechanics is a vast subject because of the wide range of solid materials available, such as steel, wood, concrete, biological materials, textiles, geological ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Revolutions Per Minute
Revolutions per minute (abbreviated rpm, RPM, rev/min, r/min, or with the notation min−1) is a unit of rotational speed or rotational frequency for rotating machines. Standards ISO 80000-3:2019 defines a unit of rotation as the dimensionless unit equal to 1, which it refers to as a revolution, but does not define the revolution as a unit. It defines a unit of rotational frequency equal to s−1. The superseded standard ISO 80000-3:2006 did however state with reference to the unit name 'one', symbol '1', that "The special name revolution, symbol r, for this unit is widely used in specifications on rotating machines." The International System of Units (SI) does not recognize rpm as a unit, and defines the unit of frequency, Hz, as equal to s−1. :\begin 1~&\text &&=& 60~&\text \\ \frac~&\text &&=& 1~&\text \end A corresponding but distinct quantity for describing rotation is angular velocity, for which the SI unit is the ra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mechanical Engineering
Mechanical engineering is the study of physical machines that may involve force and movement. It is an engineering branch that combines engineering physics and mathematics principles with materials science, to design, analyze, manufacture, and maintain mechanical systems. It is one of the oldest and broadest of the engineering branches. Mechanical engineering requires an understanding of core areas including mechanics, dynamics, thermodynamics, materials science, structural analysis, and electricity. In addition to these core principles, mechanical engineers use tools such as computer-aided design (CAD), computer-aided manufacturing (CAM), and product lifecycle management to design and analyze manufacturing plants, industrial equipment and machinery, heating and cooling systems, transport systems, aircraft, watercraft, robotics, medical devices, weapons, and others. Mechanical engineering emerged as a field during the Industrial Revolution in Europe in the 18th century; ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vibration
Vibration is a mechanical phenomenon whereby oscillations occur about an equilibrium point. The word comes from Latin ''vibrationem'' ("shaking, brandishing"). The oscillations may be periodic function, periodic, such as the motion of a pendulum—or random, such as the movement of a tire on a gravel road. Vibration can be desirable: for example, the motion of a tuning fork, the Reed (music), reed in a woodwind instrument or harmonica, a mobile phone, or the cone of a loudspeaker. In many cases, however, vibration is undesirable, wasting energy and creating unwanted sound. For example, the vibrational motions of engines, electric motors, or any Machine, mechanical device in operation are typically unwanted. Such vibrations could be caused by Engine balance, imbalances in the rotating parts, uneven friction, or the meshing of gear teeth. Careful designs usually minimize unwanted vibrations. The studies of sound and vibration are closely related. Sound, or pressure waves, are ge ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Resonance
Resonance describes the phenomenon of increased amplitude that occurs when the frequency of an applied periodic force (or a Fourier component of it) is equal or close to a natural frequency of the system on which it acts. When an oscillating force is applied at a resonant frequency of a dynamic system, the system will oscillate at a higher amplitude than when the same force is applied at other, non-resonant frequencies. Frequencies at which the response amplitude is a relative maximum are also known as resonant frequencies or resonance frequencies of the system. Small periodic forces that are near a resonant frequency of the system have the ability to produce large amplitude oscillations in the system due to the storage of vibrational energy. Resonance phenomena occur with all types of vibrations or waves: there is mechanical resonance, orbital resonance, acoustic resonance, electromagnetic resonance, nuclear magnetic resonance (NMR), electron spin resonance (ESR) and reso ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
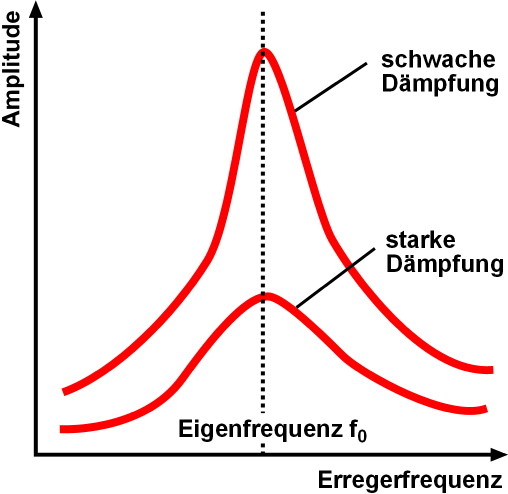
Natural Frequency
Natural frequency, also known as eigenfrequency, is the frequency at which a system tends to oscillate in the absence of any driving force. The motion pattern of a system oscillating at its natural frequency is called the normal mode (if all parts of the system move sinusoidally with that same frequency). If the oscillating system is driven by an external force at the frequency at which the amplitude of its motion is greatest (close to a natural frequency of the system), this frequency is called resonant frequency. Overview Free vibrations of an elastic body are called ''natural vibrations'' and occur at a frequency called the natural frequency. Natural vibrations are different from forced vibrations which happen at the frequency of an applied force (forced frequency). If the forced frequency is equal to the natural frequency, the vibrations' amplitude increases manyfold. This phenomenon is known as resonance. In a mass-spring system, with mass ''m'' and spring stiffness ' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Oscillate
Oscillation is the repetitive or periodic variation, typically in time, of some measure about a central value (often a point of equilibrium) or between two or more different states. Familiar examples of oscillation include a swinging pendulum and alternating current. Oscillations can be used in physics to approximate complex interactions, such as those between atoms. Oscillations occur not only in mechanical systems but also in dynamic systems in virtually every area of science: for example the beating of the human heart (for circulation), business cycles in economics, predator–prey population cycles in ecology, geothermal geysers in geology, vibration of strings in guitar and other string instruments, periodic firing of nerve cells in the brain, and the periodic swelling of Cepheid variable stars in astronomy. The term ''vibration'' is precisely used to describe a mechanical oscillation. Oscillation, especially rapid oscillation, may be an undesirable phenomenon in proce ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Damping Ratio
Damping is an influence within or upon an oscillatory system that has the effect of reducing or preventing its oscillation. In physical systems, damping is produced by processes that dissipate the energy stored in the oscillation. Examples include viscous drag (a liquid's viscosity can hinder an oscillatory system, causing it to slow down; see viscous damping) in mechanical systems, resistance in electronic oscillators, and absorption and scattering of light in optical oscillators. Damping not based on energy loss can be important in other oscillating systems such as those that occur in biological systems and bikes (ex. Suspension (mechanics)). Not to be confused with friction, which is a dissipative force acting on a system. Friction can cause or be a factor of damping. The damping ratio is a dimensionless measure describing how oscillations in a system decay after a disturbance. Many systems exhibit oscillatory behavior when they are disturbed from their position of sta ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Deflection (engineering)
In structural engineering, deflection is the degree to which a part of a structural element is displaced under a load (because it deforms). It may refer to an angle or a distance. The deflection distance of a member under a load can be calculated by integrating the function that mathematically describes the slope of the deflected shape of the member under that load. Standard formulas exist for the deflection of common beam configurations and load cases at discrete locations. Otherwise methods such as virtual work, direct integration, Castigliano's method, Macaulay's method or the direct stiffness method are used. The deflection of beam elements is usually calculated on the basis of the Euler–Bernoulli beam equation while that of a plate or shell element is calculated using plate or shell theory. An example of the use of deflection in this context is in building construction. Architects and engineers select materials for various applications. [Baidu] |
Radians
The radian, denoted by the symbol rad, is the unit of angle in the International System of Units (SI) and is the standard unit of angular measure used in many areas of mathematics. The unit was formerly an SI supplementary unit (before that category was abolished in 1995). The radian is defined in the SI as being a dimensionless unit, with 1 rad = 1. Its symbol is accordingly often omitted, especially in mathematical writing. Definition One radian is defined as the angle subtended from the center of a circle which intercepts an arc equal in length to the radius of the circle. More generally, the magnitude in radians of a subtended angle is equal to the ratio of the arc length to the radius of the circle; that is, \theta = \frac, where is the subtended angle in radians, is arc length, and is radius. A right angle is exactly \frac radians. The rotation angle (360°) corresponding to one complete revolution is the length of the circumference divided by the radius, which i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rotordynamics
Rotordynamics, also known as rotor dynamics, is a specialized branch of applied mechanics concerned with the behavior and diagnosis of rotating structures. It is commonly used to analyze the behavior of structures ranging from jet engines and steam turbines to auto engines and computer disk storage. At its most basic level, rotor dynamics is concerned with one or more mechanical structures ( rotors) supported by bearings and influenced by internal phenomena that rotate around a single axis. The supporting structure is called a stator. As the speed of rotation increases the amplitude of vibration often passes through a maximum that is called a critical speed. This amplitude is commonly excited by imbalance of the rotating structure; everyday examples include engine balance and tire balance. If the amplitude of vibration at these critical speeds is excessive, then catastrophic failure occurs. In addition to this, turbomachinery often develop instabilities which are related to the in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.jpg)