Uniform 9-polytope on:
[Wikipedia]
[Google]
[Amazon]
In nine-dimensional
Name !colspan=9, Element counts , - , , 8-faces, , 7-faces, , 6-faces, , 5-faces, , 4-faces, , Cells, , Faces, , Edges, , Vertices , - , - align=center !1 , ,
,
t0{3,3,3,3,3,3,3,3}
 ,
,
t1{3,3,3,3,3,3,3,3}
 ,
,
t2{3,3,3,3,3,3,3,3}
Birectified 9-simplex (breday) , , , , , , , , , , , , , , , , 1260 , , 120 , - align=center !4 , ,
,
t3{3,3,3,3,3,3,3,3}
Trirectified 9-simplex (treday) , , , , , , , , , , , , , , , , 2520 , , 210 , - align=center BGCOLOR="#e0f0e0" !5 , ,
,
t4{3,3,3,3,3,3,3,3}
Quadrirectified 9-simplex (icoy) , , , , , , , , , , , , , , , , 3150 , , 252 , - align=center !6 , ,
,
t0,1{3,3,3,3,3,3,3,3}
Truncated 9-simplex (teday) , , , , , , , , , , , , , , , , 405 , , 90 , - align=center !7 , ,
,
t0,2{3,3,3,3,3,3,3,3}
Cantellated 9-simplex , , , , , , , , , , , , , , , , 2880 , , 360 , - align=center !8 , ,
,
t1,2{3,3,3,3,3,3,3,3}
Bitruncated 9-simplex , , , , , , , , , , , , , , , , 1620 , , 360 , - align=center !9 , ,
,
t0,3{3,3,3,3,3,3,3,3}
Runcinated 9-simplex , , , , , , , , , , , , , , , , 8820 , , 840 , - align=center !10 , ,
,
t1,3{3,3,3,3,3,3,3,3}
Bicantellated 9-simplex , , , , , , , , , , , , , , , , 10080 , , 1260 , - align=center !11 , ,
,
t2,3{3,3,3,3,3,3,3,3}
Tritruncated 9-simplex (treday) , , , , , , , , , , , , , , , , 3780 , , 840 , - align=center !12 , ,
,
t0,4{3,3,3,3,3,3,3,3}
Stericated 9-simplex , , , , , , , , , , , , , , , , 15120 , , 1260 , - align=center !13 , ,
,
t1,4{3,3,3,3,3,3,3,3}
Biruncinated 9-simplex , , , , , , , , , , , , , , , , 26460 , , 2520 , - align=center !14 , ,
,
t2,4{3,3,3,3,3,3,3,3}
Tricantellated 9-simplex , , , , , , , , , , , , , , , , 20160 , , 2520 , - align=center !15 , ,
t3,4{3,3,3,3,3,3,3,3}
Quadritruncated 9-simplex , , , , , , , , , , , , , , , , 5670 , , 1260 , - align=center !16 , ,
,
t0,5{3,3,3,3,3,3,3,3}
Pentellated 9-simplex , , , , , , , , , , , , , , , , 15750 , , 1260 , - align=center !17 , ,
t1,5{3,3,3,3,3,3,3,3}
Bistericated 9-simplex , , , , , , , , , , , , , , , , 37800 , , 3150 , - align=center !18 , ,
t2,5{3,3,3,3,3,3,3,3}
Triruncinated 9-simplex , , , , , , , , , , , , , , , , 44100 , , 4200 , - align=center BGCOLOR="#e0f0e0" !19 , ,
t3,5{3,3,3,3,3,3,3,3}
Quadricantellated 9-simplex , , , , , , , , , , , , , , , , 25200 , , 3150 , - align=center !20 , ,
,
t0,6{3,3,3,3,3,3,3,3}
Hexicated 9-simplex , , , , , , , , , , , , , , , , 10080 , , 840 , - align=center !21 , ,
t1,6{3,3,3,3,3,3,3,3}
Bipentellated 9-simplex , , , , , , , , , , , , , , , , 31500 , , 2520 , - align=center BGCOLOR="#e0f0e0" !22 , ,
t2,6{3,3,3,3,3,3,3,3}
Tristericated 9-simplex , , , , , , , , , , , , , , , , 50400 , , 4200 , - align=center !23 , ,
,
t0,7{3,3,3,3,3,3,3,3}
Heptellated 9-simplex , , , , , , , , , , , , , , , , 3780 , , 360 , - align=center BGCOLOR="#e0f0e0" !24 , ,
t1,7{3,3,3,3,3,3,3,3}
Bihexicated 9-simplex , , , , , , , , , , , , , , , , 15120 , , 1260 , - align=center BGCOLOR="#e0f0e0" !25 , ,
,
t0,8{3,3,3,3,3,3,3,3}
Octellated 9-simplex , , , , , , , , , , , , , , , , 720 , , 90 , - align=center !26 , ,
,
t0,1,2{3,3,3,3,3,3,3,3}
Cantitruncated 9-simplex , , , , , , , , , , , , , , , , 3240 , , 720 , - align=center !27 , ,
t0,1,3{3,3,3,3,3,3,3,3}
Runcitruncated 9-simplex , , , , , , , , , , , , , , , , 18900 , , 2520 , - align=center !28 , ,
t0,2,3{3,3,3,3,3,3,3,3}
Runcicantellated 9-simplex , , , , , , , , , , , , , , , , 12600 , , 2520 , - align=center !29 , ,
,
t1,2,3{3,3,3,3,3,3,3,3}
Bicantitruncated 9-simplex , , , , , , , , , , , , , , , , 11340 , , 2520 , - align=center !30 , ,
t0,1,4{3,3,3,3,3,3,3,3}
Steritruncated 9-simplex , , , , , , , , , , , , , , , , 47880 , , 5040 , - align=center !31 , ,
t0,2,4{3,3,3,3,3,3,3,3}
Stericantellated 9-simplex , , , , , , , , , , , , , , , , 60480 , , 7560 , - align=center !32 , ,
t1,2,4{3,3,3,3,3,3,3,3}
Biruncitruncated 9-simplex , , , , , , , , , , , , , , , , 52920 , , 7560 , - align=center !33 , ,
t0,3,4{3,3,3,3,3,3,3,3}
Steriruncinated 9-simplex , , , , , , , , , , , , , , , , 27720 , , 5040 , - align=center !34 , ,
t1,3,4{3,3,3,3,3,3,3,3}
Biruncicantellated 9-simplex , , , , , , , , , , , , , , , , 41580 , , 7560 , - align=center !35 , ,
,
t2,3,4{3,3,3,3,3,3,3,3}
Tricantitruncated 9-simplex , , , , , , , , , , , , , , , , 22680 , , 5040 , - align=center !36 , ,
t0,1,5{3,3,3,3,3,3,3,3}
Pentitruncated 9-simplex , , , , , , , , , , , , , , , , 66150 , , 6300 , - align=center !37 , ,
t0,2,5{3,3,3,3,3,3,3,3}
Penticantellated 9-simplex , , , , , , , , , , , , , , , , 126000 , , 12600 , - align=center !38 , ,
t1,2,5{3,3,3,3,3,3,3,3}
Bisteritruncated 9-simplex , , , , , , , , , , , , , , , , 107100 , , 12600 , - align=center !39 , ,
t0,3,5{3,3,3,3,3,3,3,3}
Pentiruncinated 9-simplex , , , , , , , , , , , , , , , , 107100 , , 12600 , - align=center !40 , ,
t1,3,5{3,3,3,3,3,3,3,3}
Bistericantellated 9-simplex , , , , , , , , , , , , , , , , 151200 , , 18900 , - align=center !41 , ,
t2,3,5{3,3,3,3,3,3,3,3}
Triruncitruncated 9-simplex , , , , , , , , , , , , , , , , 81900 , , 12600 , - align=center !42 , ,
t0,4,5{3,3,3,3,3,3,3,3}
Pentistericated 9-simplex , , , , , , , , , , , , , , , , 37800 , , 6300 , - align=center !43 , ,
t1,4,5{3,3,3,3,3,3,3,3}
Bisteriruncinated 9-simplex , , , , , , , , , , , , , , , , 81900 , , 12600 , - align=center !44 , ,
t2,4,5{3,3,3,3,3,3,3,3}
Triruncicantellated 9-simplex , , , , , , , , , , , , , , , , 75600 , , 12600 , - align=center BGCOLOR="#e0f0e0" !45 , ,
,
t3,4,5{3,3,3,3,3,3,3,3}
Quadricantitruncated 9-simplex , , , , , , , , , , , , , , , , 28350 , , 6300 , - align=center !46 , ,
t0,1,6{3,3,3,3,3,3,3,3}
Hexitruncated 9-simplex , , , , , , , , , , , , , , , , 52920 , , 5040 , - align=center !47 , ,
t0,2,6{3,3,3,3,3,3,3,3}
Hexicantellated 9-simplex , , , , , , , , , , , , , , , , 138600 , , 12600 , - align=center !48 , ,
t1,2,6{3,3,3,3,3,3,3,3}
Bipentitruncated 9-simplex , , , , , , , , , , , , , , , , 113400 , , 12600 , - align=center !49 , ,
t0,3,6{3,3,3,3,3,3,3,3}
Hexiruncinated 9-simplex , , , , , , , , , , , , , , , , 176400 , , 16800 , - align=center !50 , ,
t1,3,6{3,3,3,3,3,3,3,3}
Bipenticantellated 9-simplex , , , , , , , , , , , , , , , , 239400 , , 25200 , - align=center !51 , ,
t2,3,6{3,3,3,3,3,3,3,3}
Tristeritruncated 9-simplex , , , , , , , , , , , , , , , , 126000 , , 16800 , - align=center !52 , ,
t0,4,6{3,3,3,3,3,3,3,3}
Hexistericated 9-simplex , , , , , , , , , , , , , , , , 113400 , , 12600 , - align=center !53 , ,
t1,4,6{3,3,3,3,3,3,3,3}
Bipentiruncinated 9-simplex , , , , , , , , , , , , , , , , 226800 , , 25200 , - align=center BGCOLOR="#e0f0e0" !54 , ,
t2,4,6{3,3,3,3,3,3,3,3}
Tristericantellated 9-simplex , , , , , , , , , , , , , , , , 201600 , , 25200 , - align=center !55 , ,
t0,5,6{3,3,3,3,3,3,3,3}
Hexipentellated 9-simplex , , , , , , , , , , , , , , , , 32760 , , 5040 , - align=center !56 , ,
t1,5,6{3,3,3,3,3,3,3,3}
Bipentistericated 9-simplex , , , , , , , , , , , , , , , , 94500 , , 12600 , - align=center !57 , ,
t0,1,7{3,3,3,3,3,3,3,3}
Heptitruncated 9-simplex , , , , , , , , , , , , , , , , 23940 , , 2520 , - align=center !58 , ,
t0,2,7{3,3,3,3,3,3,3,3}
Hepticantellated 9-simplex , , , , , , , , , , , , , , , , 83160 , , 7560 , - align=center !59 , ,
t1,2,7{3,3,3,3,3,3,3,3}
Bihexitruncated 9-simplex , , , , , , , , , , , , , , , , 64260 , , 7560 , - align=center !60 , ,
t0,3,7{3,3,3,3,3,3,3,3}
Heptiruncinated 9-simplex , , , , , , , , , , , , , , , , 144900 , , 12600 , - align=center !61 , ,
t1,3,7{3,3,3,3,3,3,3,3}
Bihexicantellated 9-simplex , , , , , , , , , , , , , , , , 189000 , , 18900 , - align=center !62 , ,
t0,4,7{3,3,3,3,3,3,3,3}
Heptistericated 9-simplex , , , , , , , , , , , , , , , , 138600 , , 12600 , - align=center BGCOLOR="#e0f0e0" !63 , ,
t1,4,7{3,3,3,3,3,3,3,3}
Bihexiruncinated 9-simplex , , , , , , , , , , , , , , , , 264600 , , 25200 , - align=center !64 , ,
t0,5,7{3,3,3,3,3,3,3,3}
Heptipentellated 9-simplex , , , , , , , , , , , , , , , , 71820 , , 7560 , - align=center !65 , ,
t0,6,7{3,3,3,3,3,3,3,3}
Heptihexicated 9-simplex , , , , , , , , , , , , , , , , 17640 , , 2520 , - align=center !66 , ,
t0,1,8{3,3,3,3,3,3,3,3}
Octitruncated 9-simplex , , , , , , , , , , , , , , , , 5400 , , 720 , - align=center !67 , ,
t0,2,8{3,3,3,3,3,3,3,3}
Octicantellated 9-simplex , , , , , , , , , , , , , , , , 25200 , , 2520 , - align=center !68 , ,
t0,3,8{3,3,3,3,3,3,3,3}
Octiruncinated 9-simplex , , , , , , , , , , , , , , , , 57960 , , 5040 , - align=center BGCOLOR="#e0f0e0" !69 , ,
t0,4,8{3,3,3,3,3,3,3,3}
Octistericated 9-simplex , , , , , , , , , , , , , , , , 75600 , , 6300 , - align=center !70 , ,
t0,1,2,3{3,3,3,3,3,3,3,3}
Runcicantitruncated 9-simplex , , , , , , , , , , , , , , , , 22680 , , 5040 , - align=center !71 , ,
t0,1,2,4{3,3,3,3,3,3,3,3}
Stericantitruncated 9-simplex , , , , , , , , , , , , , , , , 105840 , , 15120 , - align=center !72 , ,
t0,1,3,4{3,3,3,3,3,3,3,3}
Steriruncitruncated 9-simplex , , , , , , , , , , , , , , , , 75600 , , 15120 , - align=center !73 , ,
t0,2,3,4{3,3,3,3,3,3,3,3}
Steriruncicantellated 9-simplex , , , , , , , , , , , , , , , , 75600 , , 15120 , - align=center !74 , ,
t1,2,3,4{3,3,3,3,3,3,3,3}
Biruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 68040 , , 15120 , - align=center !75 , ,
t0,1,2,5{3,3,3,3,3,3,3,3}
Penticantitruncated 9-simplex , , , , , , , , , , , , , , , , 214200 , , 25200 , - align=center !76 , ,
t0,1,3,5{3,3,3,3,3,3,3,3}
Pentiruncitruncated 9-simplex , , , , , , , , , , , , , , , , 283500 , , 37800 , - align=center !77 , ,
t0,2,3,5{3,3,3,3,3,3,3,3}
Pentiruncicantellated 9-simplex , , , , , , , , , , , , , , , , 264600 , , 37800 , - align=center !78 , ,
t1,2,3,5{3,3,3,3,3,3,3,3}
Bistericantitruncated 9-simplex , , , , , , , , , , , , , , , , 245700 , , 37800 , - align=center !79 , ,
t0,1,4,5{3,3,3,3,3,3,3,3}
Pentisteritruncated 9-simplex , , , , , , , , , , , , , , , , 138600 , , 25200 , - align=center !80 , ,
t0,2,4,5{3,3,3,3,3,3,3,3}
Pentistericantellated 9-simplex , , , , , , , , , , , , , , , , 226800 , , 37800 , - align=center !81 , ,
t1,2,4,5{3,3,3,3,3,3,3,3}
Bisteriruncitruncated 9-simplex , , , , , , , , , , , , , , , , 189000 , , 37800 , - align=center !82 , ,
t0,3,4,5{3,3,3,3,3,3,3,3}
Pentisteriruncinated 9-simplex , , , , , , , , , , , , , , , , 138600 , , 25200 , - align=center !83 , ,
t1,3,4,5{3,3,3,3,3,3,3,3}
Bisteriruncicantellated 9-simplex , , , , , , , , , , , , , , , , 207900 , , 37800 , - align=center !84 , ,
t2,3,4,5{3,3,3,3,3,3,3,3}
Triruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 113400 , , 25200 , - align=center !85 , ,
t0,1,2,6{3,3,3,3,3,3,3,3}
Hexicantitruncated 9-simplex , , , , , , , , , , , , , , , , 226800 , , 25200 , - align=center !86 , ,
t0,1,3,6{3,3,3,3,3,3,3,3}
Hexiruncitruncated 9-simplex , , , , , , , , , , , , , , , , 453600 , , 50400 , - align=center !87 , ,
t0,2,3,6{3,3,3,3,3,3,3,3}
Hexiruncicantellated 9-simplex , , , , , , , , , , , , , , , , 403200 , , 50400 , - align=center !88 , ,
t1,2,3,6{3,3,3,3,3,3,3,3}
Bipenticantitruncated 9-simplex , , , , , , , , , , , , , , , , 378000 , , 50400 , - align=center !89 , ,
t0,1,4,6{3,3,3,3,3,3,3,3}
Hexisteritruncated 9-simplex , , , , , , , , , , , , , , , , 403200 , , 50400 , - align=center !90 , ,
t0,2,4,6{3,3,3,3,3,3,3,3}
Hexistericantellated 9-simplex , , , , , , , , , , , , , , , , 604800 , , 75600 , - align=center !91 , ,
t1,2,4,6{3,3,3,3,3,3,3,3}
Bipentiruncitruncated 9-simplex , , , , , , , , , , , , , , , , 529200 , , 75600 , - align=center !92 , ,
t0,3,4,6{3,3,3,3,3,3,3,3}
Hexisteriruncinated 9-simplex , , , , , , , , , , , , , , , , 352800 , , 50400 , - align=center !93 , ,
t1,3,4,6{3,3,3,3,3,3,3,3}
Bipentiruncicantellated 9-simplex , , , , , , , , , , , , , , , , 529200 , , 75600 , - align=center !94 , ,
t2,3,4,6{3,3,3,3,3,3,3,3}
Tristericantitruncated 9-simplex , , , , , , , , , , , , , , , , 302400 , , 50400 , - align=center !95 , ,
t0,1,5,6{3,3,3,3,3,3,3,3}
Hexipentitruncated 9-simplex , , , , , , , , , , , , , , , , 151200 , , 25200 , - align=center !96 , ,
t0,2,5,6{3,3,3,3,3,3,3,3}
Hexipenticantellated 9-simplex , , , , , , , , , , , , , , , , 352800 , , 50400 , - align=center !97 , ,
t1,2,5,6{3,3,3,3,3,3,3,3}
Bipentisteritruncated 9-simplex , , , , , , , , , , , , , , , , 277200 , , 50400 , - align=center !98 , ,
t0,3,5,6{3,3,3,3,3,3,3,3}
Hexipentiruncinated 9-simplex , , , , , , , , , , , , , , , , 352800 , , 50400 , - align=center !99 , ,
t1,3,5,6{3,3,3,3,3,3,3,3}
Bipentistericantellated 9-simplex , , , , , , , , , , , , , , , , 491400 , , 75600 , - align=center BGCOLOR="#e0f0e0" !100 , ,
t2,3,5,6{3,3,3,3,3,3,3,3}
Tristeriruncitruncated 9-simplex , , , , , , , , , , , , , , , , 252000 , , 50400 , - align=center !101 , ,
t0,4,5,6{3,3,3,3,3,3,3,3}
Hexipentistericated 9-simplex , , , , , , , , , , , , , , , , 151200 , , 25200 , - align=center !102 , ,
t1,4,5,6{3,3,3,3,3,3,3,3}
Bipentisteriruncinated 9-simplex , , , , , , , , , , , , , , , , 327600 , , 50400 , - align=center !103 , ,
t0,1,2,7{3,3,3,3,3,3,3,3}
Hepticantitruncated 9-simplex , , , , , , , , , , , , , , , , 128520 , , 15120 , - align=center !104 , ,
t0,1,3,7{3,3,3,3,3,3,3,3}
Heptiruncitruncated 9-simplex , , , , , , , , , , , , , , , , 359100 , , 37800 , - align=center !105 , ,
t0,2,3,7{3,3,3,3,3,3,3,3}
Heptiruncicantellated 9-simplex , , , , , , , , , , , , , , , , 302400 , , 37800 , - align=center !106 , ,
t1,2,3,7{3,3,3,3,3,3,3,3}
Bihexicantitruncated 9-simplex , , , , , , , , , , , , , , , , 283500 , , 37800 , - align=center !107 , ,
t0,1,4,7{3,3,3,3,3,3,3,3}
Heptisteritruncated 9-simplex , , , , , , , , , , , , , , , , 478800 , , 50400 , - align=center !108 , ,
t0,2,4,7{3,3,3,3,3,3,3,3}
Heptistericantellated 9-simplex , , , , , , , , , , , , , , , , 680400 , , 75600 , - align=center !109 , ,
t1,2,4,7{3,3,3,3,3,3,3,3}
Bihexiruncitruncated 9-simplex , , , , , , , , , , , , , , , , 604800 , , 75600 , - align=center !110 , ,
t0,3,4,7{3,3,3,3,3,3,3,3}
Heptisteriruncinated 9-simplex , , , , , , , , , , , , , , , , 378000 , , 50400 , - align=center !111 , ,
t1,3,4,7{3,3,3,3,3,3,3,3}
Bihexiruncicantellated 9-simplex , , , , , , , , , , , , , , , , 567000 , , 75600 , - align=center !112 , ,
t0,1,5,7{3,3,3,3,3,3,3,3}
Heptipentitruncated 9-simplex , , , , , , , , , , , , , , , , 321300 , , 37800 , - align=center !113 , ,
t0,2,5,7{3,3,3,3,3,3,3,3}
Heptipenticantellated 9-simplex , , , , , , , , , , , , , , , , 680400 , , 75600 , - align=center !114 , ,
t1,2,5,7{3,3,3,3,3,3,3,3}
Bihexisteritruncated 9-simplex , , , , , , , , , , , , , , , , 567000 , , 75600 , - align=center !115 , ,
t0,3,5,7{3,3,3,3,3,3,3,3}
Heptipentiruncinated 9-simplex , , , , , , , , , , , , , , , , 642600 , , 75600 , - align=center BGCOLOR="#e0f0e0" !116 , ,
t1,3,5,7{3,3,3,3,3,3,3,3}
Bihexistericantellated 9-simplex , , , , , , , , , , , , , , , , 907200 , , 113400 , - align=center !117 , ,
t0,4,5,7{3,3,3,3,3,3,3,3}
Heptipentistericated 9-simplex , , , , , , , , , , , , , , , , 264600 , , 37800 , - align=center !118 , ,
t0,1,6,7{3,3,3,3,3,3,3,3}
Heptihexitruncated 9-simplex , , , , , , , , , , , , , , , , 98280 , , 15120 , - align=center !119 , ,
t0,2,6,7{3,3,3,3,3,3,3,3}
Heptihexicantellated 9-simplex , , , , , , , , , , , , , , , , 302400 , , 37800 , - align=center BGCOLOR="#e0f0e0" !120 , ,
t1,2,6,7{3,3,3,3,3,3,3,3}
Bihexipentitruncated 9-simplex , , , , , , , , , , , , , , , , 226800 , , 37800 , - align=center !121 , ,
t0,3,6,7{3,3,3,3,3,3,3,3}
Heptihexiruncinated 9-simplex , , , , , , , , , , , , , , , , 428400 , , 50400 , - align=center !122 , ,
t0,4,6,7{3,3,3,3,3,3,3,3}
Heptihexistericated 9-simplex , , , , , , , , , , , , , , , , 302400 , , 37800 , - align=center !123 , ,
t0,5,6,7{3,3,3,3,3,3,3,3}
Heptihexipentellated 9-simplex , , , , , , , , , , , , , , , , 98280 , , 15120 , - align=center !124 , ,
t0,1,2,8{3,3,3,3,3,3,3,3}
Octicantitruncated 9-simplex , , , , , , , , , , , , , , , , 35280 , , 5040 , - align=center !125 , ,
t0,1,3,8{3,3,3,3,3,3,3,3}
Octiruncitruncated 9-simplex , , , , , , , , , , , , , , , , 136080 , , 15120 , - align=center !126 , ,
t0,2,3,8{3,3,3,3,3,3,3,3}
Octiruncicantellated 9-simplex , , , , , , , , , , , , , , , , 105840 , , 15120 , - align=center !127 , ,
t0,1,4,8{3,3,3,3,3,3,3,3}
Octisteritruncated 9-simplex , , , , , , , , , , , , , , , , 252000 , , 25200 , - align=center !128 , ,
t0,2,4,8{3,3,3,3,3,3,3,3}
Octistericantellated 9-simplex , , , , , , , , , , , , , , , , 340200 , , 37800 , - align=center !129 , ,
t0,3,4,8{3,3,3,3,3,3,3,3}
Octisteriruncinated 9-simplex , , , , , , , , , , , , , , , , 176400 , , 25200 , - align=center !130 , ,
t0,1,5,8{3,3,3,3,3,3,3,3}
Octipentitruncated 9-simplex , , , , , , , , , , , , , , , , 252000 , , 25200 , - align=center !131 , ,
t0,2,5,8{3,3,3,3,3,3,3,3}
Octipenticantellated 9-simplex , , , , , , , , , , , , , , , , 504000 , , 50400 , - align=center BGCOLOR="#e0f0e0" !132 , ,
t0,3,5,8{3,3,3,3,3,3,3,3}
Octipentiruncinated 9-simplex , , , , , , , , , , , , , , , , 453600 , , 50400 , - align=center !133 , ,
t0,1,6,8{3,3,3,3,3,3,3,3}
Octihexitruncated 9-simplex , , , , , , , , , , , , , , , , 136080 , , 15120 , - align=center BGCOLOR="#e0f0e0" !134 , ,
t0,2,6,8{3,3,3,3,3,3,3,3}
Octihexicantellated 9-simplex , , , , , , , , , , , , , , , , 378000 , , 37800 , - align=center BGCOLOR="#e0f0e0" !135 , ,
t0,1,7,8{3,3,3,3,3,3,3,3}
Octiheptitruncated 9-simplex , , , , , , , , , , , , , , , , 35280 , , 5040 , - align=center !136 , ,
t0,1,2,3,4{3,3,3,3,3,3,3,3}
Steriruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 136080 , , 30240 , - align=center !137 , ,
t0,1,2,3,5{3,3,3,3,3,3,3,3}
Pentiruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 491400 , , 75600 , - align=center !138 , ,
t0,1,2,4,5{3,3,3,3,3,3,3,3}
Pentistericantitruncated 9-simplex , , , , , , , , , , , , , , , , 378000 , , 75600 , - align=center !139 , ,
t0,1,3,4,5{3,3,3,3,3,3,3,3}
Pentisteriruncitruncated 9-simplex , , , , , , , , , , , , , , , , 378000 , , 75600 , - align=center !140 , ,
t0,2,3,4,5{3,3,3,3,3,3,3,3}
Pentisteriruncicantellated 9-simplex , , , , , , , , , , , , , , , , 378000 , , 75600 , - align=center !141 , ,
t1,2,3,4,5{3,3,3,3,3,3,3,3}
Bisteriruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 340200 , , 75600 , - align=center !142 , ,
t0,1,2,3,6{3,3,3,3,3,3,3,3}
Hexiruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 756000 , , 100800 , - align=center !143 , ,
t0,1,2,4,6{3,3,3,3,3,3,3,3}
Hexistericantitruncated 9-simplex , , , , , , , , , , , , , , , , 1058400 , , 151200 , - align=center !144 , ,
t0,1,3,4,6{3,3,3,3,3,3,3,3}
Hexisteriruncitruncated 9-simplex , , , , , , , , , , , , , , , , 982800 , , 151200 , - align=center !145 , ,
t0,2,3,4,6{3,3,3,3,3,3,3,3}
Hexisteriruncicantellated 9-simplex , , , , , , , , , , , , , , , , 982800 , , 151200 , - align=center !146 , ,
t1,2,3,4,6{3,3,3,3,3,3,3,3}
Bipentiruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 907200 , , 151200 , - align=center !147 , ,
t0,1,2,5,6{3,3,3,3,3,3,3,3}
Hexipenticantitruncated 9-simplex , , , , , , , , , , , , , , , , 554400 , , 100800 , - align=center !148 , ,
t0,1,3,5,6{3,3,3,3,3,3,3,3}
Hexipentiruncitruncated 9-simplex , , , , , , , , , , , , , , , , 907200 , , 151200 , - align=center !149 , ,
t0,2,3,5,6{3,3,3,3,3,3,3,3}
Hexipentiruncicantellated 9-simplex , , , , , , , , , , , , , , , , 831600 , , 151200 , - align=center !150 , ,
t1,2,3,5,6{3,3,3,3,3,3,3,3}
Bipentistericantitruncated 9-simplex , , , , , , , , , , , , , , , , 756000 , , 151200 , - align=center !151 , ,
t0,1,4,5,6{3,3,3,3,3,3,3,3}
Hexipentisteritruncated 9-simplex , , , , , , , , , , , , , , , , 554400 , , 100800 , - align=center !152 , ,
t0,2,4,5,6{3,3,3,3,3,3,3,3}
Hexipentistericantellated 9-simplex , , , , , , , , , , , , , , , , 907200 , , 151200 , - align=center !153 , ,
t1,2,4,5,6{3,3,3,3,3,3,3,3}
Bipentisteriruncitruncated 9-simplex , , , , , , , , , , , , , , , , 756000 , , 151200 , - align=center !154 , ,
t0,3,4,5,6{3,3,3,3,3,3,3,3}
Hexipentisteriruncinated 9-simplex , , , , , , , , , , , , , , , , 554400 , , 100800 , - align=center !155 , ,
t1,3,4,5,6{3,3,3,3,3,3,3,3}
Bipentisteriruncicantellated 9-simplex , , , , , , , , , , , , , , , , 831600 , , 151200 , - align=center BGCOLOR="#e0f0e0" !156 , ,
t2,3,4,5,6{3,3,3,3,3,3,3,3}
Tristeriruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 453600 , , 100800 , - align=center !157 , ,
t0,1,2,3,7{3,3,3,3,3,3,3,3}
Heptiruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 567000 , , 75600 , - align=center !158 , ,
t0,1,2,4,7{3,3,3,3,3,3,3,3}
Heptistericantitruncated 9-simplex , , , , , , , , , , , , , , , , 1209600 , , 151200 , - align=center !159 , ,
t0,1,3,4,7{3,3,3,3,3,3,3,3}
Heptisteriruncitruncated 9-simplex , , , , , , , , , , , , , , , , 1058400 , , 151200 , - align=center !160 , ,
t0,2,3,4,7{3,3,3,3,3,3,3,3}
Heptisteriruncicantellated 9-simplex , , , , , , , , , , , , , , , , 1058400 , , 151200 , - align=center !161 , ,
t1,2,3,4,7{3,3,3,3,3,3,3,3}
Bihexiruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 982800 , , 151200 , - align=center !162 , ,
t0,1,2,5,7{3,3,3,3,3,3,3,3}
Heptipenticantitruncated 9-simplex , , , , , , , , , , , , , , , , 1134000 , , 151200 , - align=center !163 , ,
t0,1,3,5,7{3,3,3,3,3,3,3,3}
Heptipentiruncitruncated 9-simplex , , , , , , , , , , , , , , , , 1701000 , , 226800 , - align=center !164 , ,
t0,2,3,5,7{3,3,3,3,3,3,3,3}
Heptipentiruncicantellated 9-simplex , , , , , , , , , , , , , , , , 1587600 , , 226800 , - align=center !165 , ,
t1,2,3,5,7{3,3,3,3,3,3,3,3}
Bihexistericantitruncated 9-simplex , , , , , , , , , , , , , , , , 1474200 , , 226800 , - align=center !166 , ,
t0,1,4,5,7{3,3,3,3,3,3,3,3}
Heptipentisteritruncated 9-simplex , , , , , , , , , , , , , , , , 982800 , , 151200 , - align=center !167 , ,
t0,2,4,5,7{3,3,3,3,3,3,3,3}
Heptipentistericantellated 9-simplex , , , , , , , , , , , , , , , , 1587600 , , 226800 , - align=center !168 , ,
t1,2,4,5,7{3,3,3,3,3,3,3,3}
Bihexisteriruncitruncated 9-simplex , , , , , , , , , , , , , , , , 1360800 , , 226800 , - align=center !169 , ,
t0,3,4,5,7{3,3,3,3,3,3,3,3}
Heptipentisteriruncinated 9-simplex , , , , , , , , , , , , , , , , 982800 , , 151200 , - align=center BGCOLOR="#e0f0e0" !170 , ,
t1,3,4,5,7{3,3,3,3,3,3,3,3}
Bihexisteriruncicantellated 9-simplex , , , , , , , , , , , , , , , , 1474200 , , 226800 , - align=center !171 , ,
t0,1,2,6,7{3,3,3,3,3,3,3,3}
Heptihexicantitruncated 9-simplex , , , , , , , , , , , , , , , , 453600 , , 75600 , - align=center !172 , ,
t0,1,3,6,7{3,3,3,3,3,3,3,3}
Heptihexiruncitruncated 9-simplex , , , , , , , , , , , , , , , , 1058400 , , 151200 , - align=center !173 , ,
t0,2,3,6,7{3,3,3,3,3,3,3,3}
Heptihexiruncicantellated 9-simplex , , , , , , , , , , , , , , , , 907200 , , 151200 , - align=center !174 , ,
t1,2,3,6,7{3,3,3,3,3,3,3,3}
Bihexipenticantitruncated 9-simplex , , , , , , , , , , , , , , , , 831600 , , 151200 , - align=center !175 , ,
t0,1,4,6,7{3,3,3,3,3,3,3,3}
Heptihexisteritruncated 9-simplex , , , , , , , , , , , , , , , , 1058400 , , 151200 , - align=center !176 , ,
t0,2,4,6,7{3,3,3,3,3,3,3,3}
Heptihexistericantellated 9-simplex , , , , , , , , , , , , , , , , 1587600 , , 226800 , - align=center BGCOLOR="#e0f0e0" !177 , ,
t1,2,4,6,7{3,3,3,3,3,3,3,3}
Bihexipentiruncitruncated 9-simplex , , , , , , , , , , , , , , , , 1360800 , , 226800 , - align=center !178 , ,
t0,3,4,6,7{3,3,3,3,3,3,3,3}
Heptihexisteriruncinated 9-simplex , , , , , , , , , , , , , , , , 907200 , , 151200 , - align=center !179 , ,
t0,1,5,6,7{3,3,3,3,3,3,3,3}
Heptihexipentitruncated 9-simplex , , , , , , , , , , , , , , , , 453600 , , 75600 , - align=center !180 , ,
t0,2,5,6,7{3,3,3,3,3,3,3,3}
Heptihexipenticantellated 9-simplex , , , , , , , , , , , , , , , , 1058400 , , 151200 , - align=center !181 , ,
t0,3,5,6,7{3,3,3,3,3,3,3,3}
Heptihexipentiruncinated 9-simplex , , , , , , , , , , , , , , , , 1058400 , , 151200 , - align=center !182 , ,
t0,4,5,6,7{3,3,3,3,3,3,3,3}
Heptihexipentistericated 9-simplex , , , , , , , , , , , , , , , , 453600 , , 75600 , - align=center !183 , ,
t0,1,2,3,8{3,3,3,3,3,3,3,3}
Octiruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 196560 , , 30240 , - align=center !184 , ,
t0,1,2,4,8{3,3,3,3,3,3,3,3}
Octistericantitruncated 9-simplex , , , , , , , , , , , , , , , , 604800 , , 75600 , - align=center !185 , ,
t0,1,3,4,8{3,3,3,3,3,3,3,3}
Octisteriruncitruncated 9-simplex , , , , , , , , , , , , , , , , 491400 , , 75600 , - align=center !186 , ,
t0,2,3,4,8{3,3,3,3,3,3,3,3}
Octisteriruncicantellated 9-simplex , , , , , , , , , , , , , , , , 491400 , , 75600 , - align=center !187 , ,
t0,1,2,5,8{3,3,3,3,3,3,3,3}
Octipenticantitruncated 9-simplex , , , , , , , , , , , , , , , , 856800 , , 100800 , - align=center !188 , ,
t0,1,3,5,8{3,3,3,3,3,3,3,3}
Octipentiruncitruncated 9-simplex , , , , , , , , , , , , , , , , 1209600 , , 151200 , - align=center !189 , ,
t0,2,3,5,8{3,3,3,3,3,3,3,3}
Octipentiruncicantellated 9-simplex , , , , , , , , , , , , , , , , 1134000 , , 151200 , - align=center !190 , ,
t0,1,4,5,8{3,3,3,3,3,3,3,3}
Octipentisteritruncated 9-simplex , , , , , , , , , , , , , , , , 655200 , , 100800 , - align=center !191 , ,
t0,2,4,5,8{3,3,3,3,3,3,3,3}
Octipentistericantellated 9-simplex , , , , , , , , , , , , , , , , 1058400 , , 151200 , - align=center BGCOLOR="#e0f0e0" !192 , ,
t0,3,4,5,8{3,3,3,3,3,3,3,3}
Octipentisteriruncinated 9-simplex , , , , , , , , , , , , , , , , 655200 , , 100800 , - align=center !193 , ,
t0,1,2,6,8{3,3,3,3,3,3,3,3}
Octihexicantitruncated 9-simplex , , , , , , , , , , , , , , , , 604800 , , 75600 , - align=center !194 , ,
t0,1,3,6,8{3,3,3,3,3,3,3,3}
Octihexiruncitruncated 9-simplex , , , , , , , , , , , , , , , , 1285200 , , 151200 , - align=center !195 , ,
t0,2,3,6,8{3,3,3,3,3,3,3,3}
Octihexiruncicantellated 9-simplex , , , , , , , , , , , , , , , , 1134000 , , 151200 , - align=center !196 , ,
t0,1,4,6,8{3,3,3,3,3,3,3,3}
Octihexisteritruncated 9-simplex , , , , , , , , , , , , , , , , 1209600 , , 151200 , - align=center BGCOLOR="#e0f0e0" !197 , ,
t0,2,4,6,8{3,3,3,3,3,3,3,3}
Octihexistericantellated 9-simplex , , , , , , , , , , , , , , , , 1814400 , , 226800 , - align=center !198 , ,
t0,1,5,6,8{3,3,3,3,3,3,3,3}
Octihexipentitruncated 9-simplex , , , , , , , , , , , , , , , , 491400 , , 75600 , - align=center !199 , ,
t0,1,2,7,8{3,3,3,3,3,3,3,3}
Octihepticantitruncated 9-simplex , , , , , , , , , , , , , , , , 196560 , , 30240 , - align=center !200 , ,
t0,1,3,7,8{3,3,3,3,3,3,3,3}
Octiheptiruncitruncated 9-simplex , , , , , , , , , , , , , , , , 604800 , , 75600 , - align=center BGCOLOR="#e0f0e0" !201 , ,
t0,1,4,7,8{3,3,3,3,3,3,3,3}
Octiheptisteritruncated 9-simplex , , , , , , , , , , , , , , , , 856800 , , 100800 , - align=center !202 , ,
t0,1,2,3,4,5{3,3,3,3,3,3,3,3}
Pentisteriruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 680400 , , 151200 , - align=center !203 , ,
t0,1,2,3,4,6{3,3,3,3,3,3,3,3}
Hexisteriruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 1814400 , , 302400 , - align=center !204 , ,
t0,1,2,3,5,6{3,3,3,3,3,3,3,3}
Hexipentiruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 1512000 , , 302400 , - align=center !205 , ,
t0,1,2,4,5,6{3,3,3,3,3,3,3,3}
Hexipentistericantitruncated 9-simplex , , , , , , , , , , , , , , , , 1512000 , , 302400 , - align=center !206 , ,
t0,1,3,4,5,6{3,3,3,3,3,3,3,3}
Hexipentisteriruncitruncated 9-simplex , , , , , , , , , , , , , , , , 1512000 , , 302400 , - align=center !207 , ,
t0,2,3,4,5,6{3,3,3,3,3,3,3,3}
Hexipentisteriruncicantellated 9-simplex , , , , , , , , , , , , , , , , 1512000 , , 302400 , - align=center !208 , ,
t1,2,3,4,5,6{3,3,3,3,3,3,3,3}
Bipentisteriruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 1360800 , , 302400 , - align=center !209 , ,
t0,1,2,3,4,7{3,3,3,3,3,3,3,3}
Heptisteriruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 1965600 , , 302400 , - align=center !210 , ,
t0,1,2,3,5,7{3,3,3,3,3,3,3,3}
Heptipentiruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 2948400 , , 453600 , - align=center !211 , ,
t0,1,2,4,5,7{3,3,3,3,3,3,3,3}
Heptipentistericantitruncated 9-simplex , , , , , , , , , , , , , , , , 2721600 , , 453600 , - align=center !212 , ,
t0,1,3,4,5,7{3,3,3,3,3,3,3,3}
Heptipentisteriruncitruncated 9-simplex , , , , , , , , , , , , , , , , 2721600 , , 453600 , - align=center !213 , ,
t0,2,3,4,5,7{3,3,3,3,3,3,3,3}
Heptipentisteriruncicantellated 9-simplex , , , , , , , , , , , , , , , , 2721600 , , 453600 , - align=center !214 , ,
t1,2,3,4,5,7{3,3,3,3,3,3,3,3}
Bihexisteriruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 2494800 , , 453600 , - align=center !215 , ,
t0,1,2,3,6,7{3,3,3,3,3,3,3,3}
Heptihexiruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 1663200 , , 302400 , - align=center !216 , ,
t0,1,2,4,6,7{3,3,3,3,3,3,3,3}
Heptihexistericantitruncated 9-simplex , , , , , , , , , , , , , , , , 2721600 , , 453600 , - align=center !217 , ,
t0,1,3,4,6,7{3,3,3,3,3,3,3,3}
Heptihexisteriruncitruncated 9-simplex , , , , , , , , , , , , , , , , 2494800 , , 453600 , - align=center !218 , ,
t0,2,3,4,6,7{3,3,3,3,3,3,3,3}
Heptihexisteriruncicantellated 9-simplex , , , , , , , , , , , , , , , , 2494800 , , 453600 , - align=center !219 , ,
t1,2,3,4,6,7{3,3,3,3,3,3,3,3}
Bihexipentiruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 2268000 , , 453600 , - align=center !220 , ,
t0,1,2,5,6,7{3,3,3,3,3,3,3,3}
Heptihexipenticantitruncated 9-simplex , , , , , , , , , , , , , , , , 1663200 , , 302400 , - align=center !221 , ,
t0,1,3,5,6,7{3,3,3,3,3,3,3,3}
Heptihexipentiruncitruncated 9-simplex , , , , , , , , , , , , , , , , 2721600 , , 453600 , - align=center !222 , ,
t0,2,3,5,6,7{3,3,3,3,3,3,3,3}
Heptihexipentiruncicantellated 9-simplex , , , , , , , , , , , , , , , , 2494800 , , 453600 , - align=center BGCOLOR="#e0f0e0" !223 , ,
t1,2,3,5,6,7{3,3,3,3,3,3,3,3}
Bihexipentistericantitruncated 9-simplex , , , , , , , , , , , , , , , , 2268000 , , 453600 , - align=center !224 , ,
t0,1,4,5,6,7{3,3,3,3,3,3,3,3}
Heptihexipentisteritruncated 9-simplex , , , , , , , , , , , , , , , , 1663200 , , 302400 , - align=center !225 , ,
t0,2,4,5,6,7{3,3,3,3,3,3,3,3}
Heptihexipentistericantellated 9-simplex , , , , , , , , , , , , , , , , 2721600 , , 453600 , - align=center !226 , ,
t0,3,4,5,6,7{3,3,3,3,3,3,3,3}
Heptihexipentisteriruncinated 9-simplex , , , , , , , , , , , , , , , , 1663200 , , 302400 , - align=center !227 , ,
t0,1,2,3,4,8{3,3,3,3,3,3,3,3}
Octisteriruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 907200 , , 151200 , - align=center !228 , ,
t0,1,2,3,5,8{3,3,3,3,3,3,3,3}
Octipentiruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 2116800 , , 302400 , - align=center !229 , ,
t0,1,2,4,5,8{3,3,3,3,3,3,3,3}
Octipentistericantitruncated 9-simplex , , , , , , , , , , , , , , , , 1814400 , , 302400 , - align=center !230 , ,
t0,1,3,4,5,8{3,3,3,3,3,3,3,3}
Octipentisteriruncitruncated 9-simplex , , , , , , , , , , , , , , , , 1814400 , , 302400 , - align=center !231 , ,
t0,2,3,4,5,8{3,3,3,3,3,3,3,3}
Octipentisteriruncicantellated 9-simplex , , , , , , , , , , , , , , , , 1814400 , , 302400 , - align=center !232 , ,
t0,1,2,3,6,8{3,3,3,3,3,3,3,3}
Octihexiruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 2116800 , , 302400 , - align=center !233 , ,
t0,1,2,4,6,8{3,3,3,3,3,3,3,3}
Octihexistericantitruncated 9-simplex , , , , , , , , , , , , , , , , 3175200 , , 453600 , - align=center !234 , ,
t0,1,3,4,6,8{3,3,3,3,3,3,3,3}
Octihexisteriruncitruncated 9-simplex , , , , , , , , , , , , , , , , 2948400 , , 453600 , - align=center !235 , ,
t0,2,3,4,6,8{3,3,3,3,3,3,3,3}
Octihexisteriruncicantellated 9-simplex , , , , , , , , , , , , , , , , 2948400 , , 453600 , - align=center !236 , ,
t0,1,2,5,6,8{3,3,3,3,3,3,3,3}
Octihexipenticantitruncated 9-simplex , , , , , , , , , , , , , , , , 1814400 , , 302400 , - align=center !237 , ,
t0,1,3,5,6,8{3,3,3,3,3,3,3,3}
Octihexipentiruncitruncated 9-simplex , , , , , , , , , , , , , , , , 2948400 , , 453600 , - align=center BGCOLOR="#e0f0e0" !238 , ,
t0,2,3,5,6,8{3,3,3,3,3,3,3,3}
Octihexipentiruncicantellated 9-simplex , , , , , , , , , , , , , , , , 2721600 , , 453600 , - align=center !239 , ,
t0,1,4,5,6,8{3,3,3,3,3,3,3,3}
Octihexipentisteritruncated 9-simplex , , , , , , , , , , , , , , , , 1814400 , , 302400 , - align=center !240 , ,
t0,1,2,3,7,8{3,3,3,3,3,3,3,3}
Octiheptiruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 907200 , , 151200 , - align=center !241 , ,
t0,1,2,4,7,8{3,3,3,3,3,3,3,3}
Octiheptistericantitruncated 9-simplex , , , , , , , , , , , , , , , , 2116800 , , 302400 , - align=center !242 , ,
t0,1,3,4,7,8{3,3,3,3,3,3,3,3}
Octiheptisteriruncitruncated 9-simplex , , , , , , , , , , , , , , , , 1814400 , , 302400 , - align=center !243 , ,
t0,1,2,5,7,8{3,3,3,3,3,3,3,3}
Octiheptipenticantitruncated 9-simplex , , , , , , , , , , , , , , , , 2116800 , , 302400 , - align=center BGCOLOR="#e0f0e0" !244 , ,
t0,1,3,5,7,8{3,3,3,3,3,3,3,3}
Octiheptipentiruncitruncated 9-simplex , , , , , , , , , , , , , , , , 3175200 , , 453600 , - align=center BGCOLOR="#e0f0e0" !245 , ,
t0,1,2,6,7,8{3,3,3,3,3,3,3,3}
Octiheptihexicantitruncated 9-simplex , , , , , , , , , , , , , , , , 907200 , , 151200 , - align=center !246 , ,
t0,1,2,3,4,5,6{3,3,3,3,3,3,3,3}
Hexipentisteriruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 2721600 , , 604800 , - align=center !247 , ,
t0,1,2,3,4,5,7{3,3,3,3,3,3,3,3}
Heptipentisteriruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 4989600 , , 907200 , - align=center !248 , ,
t0,1,2,3,4,6,7{3,3,3,3,3,3,3,3}
Heptihexisteriruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 4536000 , , 907200 , - align=center !249 , ,
t0,1,2,3,5,6,7{3,3,3,3,3,3,3,3}
Heptihexipentiruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 4536000 , , 907200 , - align=center !250 , ,
t0,1,2,4,5,6,7{3,3,3,3,3,3,3,3}
Heptihexipentistericantitruncated 9-simplex , , , , , , , , , , , , , , , , 4536000 , , 907200 , - align=center !251 , ,
t0,1,3,4,5,6,7{3,3,3,3,3,3,3,3}
Heptihexipentisteriruncitruncated 9-simplex , , , , , , , , , , , , , , , , 4536000 , , 907200 , - align=center !252 , ,
t0,2,3,4,5,6,7{3,3,3,3,3,3,3,3}
Heptihexipentisteriruncicantellated 9-simplex , , , , , , , , , , , , , , , , 4536000 , , 907200 , - align=center BGCOLOR="#e0f0e0" !253 , ,
t1,2,3,4,5,6,7{3,3,3,3,3,3,3,3}
Bihexipentisteriruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 4082400 , , 907200 , - align=center !254 , ,
t0,1,2,3,4,5,8{3,3,3,3,3,3,3,3}
Octipentisteriruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 3326400 , , 604800 , - align=center !255 , ,
t0,1,2,3,4,6,8{3,3,3,3,3,3,3,3}
Octihexisteriruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 5443200 , , 907200 , - align=center !256 , ,
t0,1,2,3,5,6,8{3,3,3,3,3,3,3,3}
Octihexipentiruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 4989600 , , 907200 , - align=center !257 , ,
t0,1,2,4,5,6,8{3,3,3,3,3,3,3,3}
Octihexipentistericantitruncated 9-simplex , , , , , , , , , , , , , , , , 4989600 , , 907200 , - align=center !258 , ,
t0,1,3,4,5,6,8{3,3,3,3,3,3,3,3}
Octihexipentisteriruncitruncated 9-simplex , , , , , , , , , , , , , , , , 4989600 , , 907200 , - align=center BGCOLOR="#e0f0e0" !259 , ,
t0,2,3,4,5,6,8{3,3,3,3,3,3,3,3}
Octihexipentisteriruncicantellated 9-simplex , , , , , , , , , , , , , , , , 4989600 , , 907200 , - align=center !260 , ,
t0,1,2,3,4,7,8{3,3,3,3,3,3,3,3}
Octiheptisteriruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 3326400 , , 604800 , - align=center !261 , ,
t0,1,2,3,5,7,8{3,3,3,3,3,3,3,3}
Octiheptipentiruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 5443200 , , 907200 , - align=center !262 , ,
t0,1,2,4,5,7,8{3,3,3,3,3,3,3,3}
Octiheptipentistericantitruncated 9-simplex , , , , , , , , , , , , , , , , 4989600 , , 907200 , - align=center BGCOLOR="#e0f0e0" !263 , ,
t0,1,3,4,5,7,8{3,3,3,3,3,3,3,3}
Octiheptipentisteriruncitruncated 9-simplex , , , , , , , , , , , , , , , , 4989600 , , 907200 , - align=center !264 , ,
t0,1,2,3,6,7,8{3,3,3,3,3,3,3,3}
Octiheptihexiruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 3326400 , , 604800 , - align=center BGCOLOR="#e0f0e0" !265 , ,
t0,1,2,4,6,7,8{3,3,3,3,3,3,3,3}
Octiheptihexistericantitruncated 9-simplex , , , , , , , , , , , , , , , , 5443200 , , 907200 , - align=center !266 , ,
t0,1,2,3,4,5,6,7{3,3,3,3,3,3,3,3}
Heptihexipentisteriruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 8164800 , , 1814400 , - align=center !267 , ,
t0,1,2,3,4,5,6,8{3,3,3,3,3,3,3,3}
Octihexipentisteriruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 9072000 , , 1814400 , - align=center !268 , ,
t0,1,2,3,4,5,7,8{3,3,3,3,3,3,3,3}
Octiheptipentisteriruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 9072000 , , 1814400 , - align=center !269 , ,
t0,1,2,3,4,6,7,8{3,3,3,3,3,3,3,3}
Octiheptihexisteriruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 9072000 , , 1814400 , - align=center BGCOLOR="#e0f0e0" !270 , ,
t0,1,2,3,5,6,7,8{3,3,3,3,3,3,3,3}
Octiheptihexipentiruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 9072000 , , 1814400 , - align=center BGCOLOR="#e0f0e0" !271 , ,
t0,1,2,3,4,5,6,7,8{3,3,3,3,3,3,3,3}
Omnitruncated 9-simplex , , , , , , , , , , , , , , , , 16329600 , , 3628800
Name !colspan=10, Element counts , - ! 8-faces ! 7-faces ! 6-faces ! 5-faces ! 4-faces ! Cells ! Faces ! Edges ! Vertices , - align=center !1 , ,
,
t0{4,3,3,3,3,3,3,3}
 ,
,
t0,1{4,3,3,3,3,3,3,3}
Truncated 9-cube (ten) , , , , , , , , , , , , , , , , 2304 , , 4608 , - align=center !3 , ,
,
t1{4,3,3,3,3,3,3,3}
Rectified 9-cube (ren) , , , , , , , , , , , , , , , , 18432 , , 2304 , - align=center !4 , ,
,
t2{4,3,3,3,3,3,3,3}
Birectified 9-cube (barn) , , , , , , , , , , , , , , , , 64512 , , 4608 , - align=center !5 , ,
,
t3{4,3,3,3,3,3,3,3}
Trirectified 9-cube (tarn) , , , , , , , , , , , , , , , , 96768 , , 5376 , - align=center !6 , ,
,
t4{4,3,3,3,3,3,3,3}
Quadrirectified 9-cube (nav)
(Quadrirectified 9-orthoplex) , , , , , , , , , , , , , , , , 80640, , 4032 , - align=center !7 , ,
,
t3{3,3,3,3,3,3,3,4}
Trirectified 9-orthoplex (tarv) , , , , , , , , , , , , , , , , 40320 , , 2016 , - align=center !8 , ,
,
t2{3,3,3,3,3,3,3,4}
Birectified 9-orthoplex (brav) , , , , , , , , , , , , , , , , 12096 , , 672 , - align=center !9 , ,
,
t1{3,3,3,3,3,3,3,4}
Rectified 9-orthoplex (riv) , , , , , , , , , , , , , , , 2016 , , 144 , - align=center !10 , ,
,
t0,1{3,3,3,3,3,3,3,4}
Truncated 9-orthoplex (tiv) , , , , , , , , , , , , , , , 2160 , , 288 , - align=center !11 , ,
,
t0{3,3,3,3,3,3,3,4}
(Alternately signed) !colspan=9, Element counts !rowspan=2, Circumrad , - ! B9, , D9, , D8, , D7, , D6, , D5, , D4, , D3, , A7, , A5, , A3, , 8, , 7, , 6, , 5, , 4, , 3, , 2, , 1, , 0 , - align=center !1 , , , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,
9-demicube (henne), , (1,1,1,1,1,1,1,1,1), , 274, , 2448, , 9888, , 23520, , 36288, , 37632, , 21404, , 4608, , 256, , 1.0606601 , - align=center !2 , , , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,
Truncated 9-demicube (thenne), , (1,1,3,3,3,3,3,3,3), , , , , , , , , , , , , , , , 69120 , , 9216, , 2.8504384 , - align=center !3 , , , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,
Cantellated 9-demicube, , (1,1,1,3,3,3,3,3,3), , , , , , , , , , , , , , , , 225792 , , 21504, , 2.6692696 , - align=center !4 , , , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,
Runcinated 9-demicube, , (1,1,1,1,3,3,3,3,3), , , , , , , , , , , , , , , , 419328 , , 32256, , 2.4748735 , - align=center !5 , , , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,
Stericated 9-demicube, , (1,1,1,1,1,3,3,3,3), , , , , , , , , , , , , , , , 483840 , , 32256, , 2.2638462 , - align=center !6 , , , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,
Pentellated 9-demicube, , (1,1,1,1,1,1,3,3,3), , , , , , , , , , , , , , , , 354816 , , 21504, , 2.0310094 , - align=center !7 , , , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,
Hexicated 9-demicube, , (1,1,1,1,1,1,1,3,3), , , , , , , , , , , , , , , , 161280 , , 9216, , 1.7677668 , - align=center !8 , , , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,  , ,
, ,
Heptellated 9-demicube, , (1,1,1,1,1,1,1,1,3), , , , , , , , , , , , , , , , 41472 , , 2304, , 1.4577379
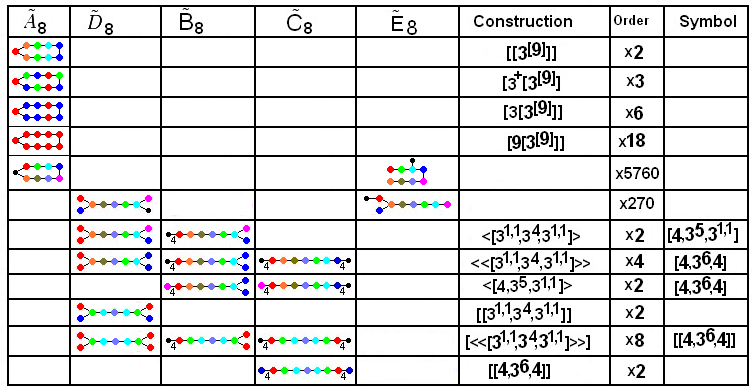 There are five fundamental affine
There are five fundamental affine
.html" ;"title="">,3[8/sup>.html" ;"title=".html" ;"title=",3 ,3[8/sup>">.html"_;"title=",3[8">,3[8/sup>
">align=right.html" ;"title="">,3[8/sup>">.html" ;"title=",3[8">,3[8/sup>
">align=right"> = align= = align= = T._Gosset:_''On_the_Regular_and_Semi-Regular_Figures_in_Space_of_n_Dimensions'',_Messenger_of_Mathematics,_Macmillan,_1900 *_ T._Gosset:_''On_the_Regular_and_Semi-Regular_Figures_in_Space_of_n_Dimensions'',_Messenger_of_Mathematics,_Macmillan,_1900 *_Alicia_Boole_Stott">A._Boole_Stott:_''Geometrical_deduction_of_semiregular_from_regular_polytopes_and_space_fillings'',_Verhandelingen_of_the_Koninklijke_academy_van_Wetenschappen_width_unit_Amsterdam,_Eerste_Sectie_11,1,_Amsterdam,_1910 *_Harold_Scott_MacDonald_Coxeter.html" ;"title="Alicia_Boole_Stott.html" ;"title="Thorold Gosset">T. Gosset: ''On the Regular and Semi-Regular Figures in Space of n Dimensions'', Messenger of Mathematics, Macmillan, 1900 * Alicia Boole Stott">A. Boole Stott: ''Geometrical deduction of semiregular from regular polytopes and space fillings'', Verhandelingen of the Koninklijke academy van Wetenschappen width unit Amsterdam, Eerste Sectie 11,1, Amsterdam, 1910 * Harold Scott MacDonald Coxeter">H.S.M. Coxeter: ** H.S.M. Coxeter, M.S. Longuet-Higgins und J.C.P. Miller: ''Uniform Polyhedra'', Philosophical Transactions of the Royal Society of London, Londne, 1954 ** H.S.M. Coxeter, ''Regular Polytopes'', 3rd Edition, Dover New York, 1973 * Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995,
** (Paper 22) H.S.M. Coxeter, ''Regular and Semi Regular Polytopes I'', [Math. Zeit. 46 (1940) 380–407, MR 2,10] ** (Paper 23) H.S.M. Coxeter, ''Regular and Semi-Regular Polytopes II'', ath. Zeit. 188 (1985) 559-591** (Paper 24) H.S.M. Coxeter, ''Regular and Semi-Regular Polytopes III'', ath. Zeit. 200 (1988) 3-45* N.W. Johnson: ''The Theory of Uniform Polytopes and Honeycombs'', Ph.D. Dissertation, University of Toronto, 1966 *
Polytope names
Jonathan Bowers
* {{Honeycombs 9-polytopes
geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is c ...
, a nine-dimensional polytope or 9-polytope is a polytope
In elementary geometry, a polytope is a geometric object with flat sides (''faces''). Polytopes are the generalization of three-dimensional polyhedra to any number of dimensions. Polytopes may exist in any general number of dimensions as an -d ...
contained by 8-polytope facets. Each 7-polytope
In seven-dimensional geometry, a 7-polytope is a polytope contained by 6-polytope facets. Each 5-polytope ridge being shared by exactly two 6-polytope facets.
A uniform 7-polytope is one whose symmetry group is transitive on vertices and whose f ...
ridge
A ridge or a mountain ridge is a geographical feature consisting of a chain of mountains or hills that form a continuous elevated crest for an extended distance. The sides of the ridge slope away from the narrow top on either side. The line ...
being shared by exactly two 8-polytope
In eight-dimensional geometry, an eight-dimensional polytope or 8-polytope is a polytope contained by 7-polytope facets. Each 6-polytope ridge being shared by exactly two 7-polytope facets.
A uniform 8-polytope is one which is vertex-transitive, ...
facets
A facet is a flat surface of a geometric shape, e.g., of a cut gemstone.
Facet may also refer to:
Arts, entertainment, and media
* ''Facets'' (album), an album by Jim Croce
* ''Facets'', a 1980 album by jazz pianist Monty Alexander and his tri ...
.
A uniform 9-polytope is one which is vertex-transitive
In geometry, a polytope (e.g. a polygon or polyhedron) or a tiling is isogonal or vertex-transitive if all its vertices are equivalent under the symmetries of the figure. This implies that each vertex is surrounded by the same kinds of face in ...
, and constructed from uniform 8-polytope
In eight-dimensional geometry, an eight-dimensional polytope or 8-polytope is a polytope contained by 7-polytope facets. Each 6-polytope ridge being shared by exactly two 7-polytope facets.
A uniform 8-polytope is one which is vertex-transiti ...
facets
A facet is a flat surface of a geometric shape, e.g., of a cut gemstone.
Facet may also refer to:
Arts, entertainment, and media
* ''Facets'' (album), an album by Jim Croce
* ''Facets'', a 1980 album by jazz pianist Monty Alexander and his tri ...
.
Regular 9-polytopes
Regular 9-polytopes can be represented by theSchläfli symbol
In geometry, the Schläfli symbol is a notation of the form \ that defines regular polytopes and tessellations.
The Schläfli symbol is named after the 19th-century Swiss mathematician Ludwig Schläfli, who generalized Euclidean geometry to more ...
, with w 8-polytope facets
A facet is a flat surface of a geometric shape, e.g., of a cut gemstone.
Facet may also refer to:
Arts, entertainment, and media
* ''Facets'' (album), an album by Jim Croce
* ''Facets'', a 1980 album by jazz pianist Monty Alexander and his tri ...
around each peak Peak or The Peak may refer to:
Basic meanings Geology
* Mountain peak
** Pyramidal peak, a mountaintop that has been sculpted by erosion to form a point Mathematics
* Peak hour or rush hour, in traffic congestion
* Peak (geometry), an (''n''-3)-di ...
.
There are exactly three such convex regular 9-polytopes:
# - 9-simplex
In geometry, a 9- simplex is a self-dual regular 9-polytope. It has 10 vertices, 45 edges, 120 triangle faces, 210 tetrahedral cells, 252 5-cell 4-faces, 210 5-simplex 5-faces, 120 6-simplex 6-faces, 45 7-simplex 7-faces, and 10 8-simplex 8-fa ...
# - 9-cube
In geometry, a 9-cube is a nine-dimensional hypercube with 512 vertices, 2304 edges, 4608 square faces, 5376 cubic cells, 4032 tesseract 4-faces, 2016 5-cube 5-faces, 672 6-cube 6-faces, 144 7-cube 7-faces, and 18 8-cube 8-faces.
It can be ...
# - 9-orthoplex
In geometry, a 9-orthoplex or 9-cross polytope, is a regular 9-polytope with 18 vertices, 144 edges, 672 triangle faces, 2016 tetrahedron cells, 4032 5-cells ''4-faces'', 5376 5-simplex ''5-faces'', 4608 6-simplex ''6-faces'', 2304 7-simplex '' ...
There are no nonconvex regular 9-polytopes.
Euler characteristic
The topology of any given 9-polytope is defined by itsBetti number
In algebraic topology, the Betti numbers are used to distinguish topological spaces based on the connectivity of ''n''-dimensional simplicial complexes. For the most reasonable finite-dimensional spaces (such as compact manifolds, finite simplicia ...
s and torsion coefficient
A torsion spring is a spring that works by twisting its end along its axis; that is, a flexible elastic object that stores mechanical energy when it is twisted. When it is twisted, it exerts a torque in the opposite direction, proportional ...
s.Richeson, D.; ''Euler's Gem: The Polyhedron Formula and the Birth of Topoplogy'', Princeton, 2008.
The value of the Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic (or Euler number, or Euler–Poincaré characteristic) is a topological invariant, a number that describes a topological space ...
used to characterise polyhedra does not generalize usefully to higher dimensions, whatever their underlying topology. This inadequacy of the Euler characteristic to reliably distinguish between different topologies in higher dimensions led to the discovery of the more sophisticated Betti numbers.
Similarly, the notion of orientability of a polyhedron is insufficient to characterise the surface twistings of toroidal polytopes, and this led to the use of torsion coefficients.
Uniform 9-polytopes by fundamental Coxeter groups
Uniform 9-polytopes with reflective symmetry can be generated by these three Coxeter groups, represented by permutations of rings of the Coxeter-Dynkin diagrams: Selected regular and uniform 9-polytopes from each family include: *Simplex
In geometry, a simplex (plural: simplexes or simplices) is a generalization of the notion of a triangle or tetrahedron to arbitrary dimensions. The simplex is so-named because it represents the simplest possible polytope in any given dimension. ...
family: A9 8-
** 271 uniform 9-polytopes as permutations of rings in the group diagram, including one regular:
**# - 9-simplex
In geometry, a 9- simplex is a self-dual regular 9-polytope. It has 10 vertices, 45 edges, 120 triangle faces, 210 tetrahedral cells, 252 5-cell 4-faces, 210 5-simplex 5-faces, 120 6-simplex 6-faces, 45 7-simplex 7-faces, and 10 8-simplex 8-fa ...
or deca-9-tope or decayotton -
* Hypercube
In geometry, a hypercube is an ''n''-dimensional analogue of a square () and a cube (). It is a closed, compact, convex figure whose 1- skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, ...
/orthoplex
In geometry, a cross-polytope, hyperoctahedron, orthoplex, or cocube is a regular, convex polytope that exists in ''n''- dimensional Euclidean space. A 2-dimensional cross-polytope is a square, a 3-dimensional cross-polytope is a regular octahed ...
family: B9 ,38-
** 511 uniform 9-polytopes as permutations of rings in the group diagram, including two regular ones:
**# - 9-cube
In geometry, a 9-cube is a nine-dimensional hypercube with 512 vertices, 2304 edges, 4608 square faces, 5376 cubic cells, 4032 tesseract 4-faces, 2016 5-cube 5-faces, 672 6-cube 6-faces, 144 7-cube 7-faces, and 18 8-cube 8-faces.
It can be ...
or enneract -
**# - 9-orthoplex
In geometry, a 9-orthoplex or 9-cross polytope, is a regular 9-polytope with 18 vertices, 144 edges, 672 triangle faces, 2016 tetrahedron cells, 4032 5-cells ''4-faces'', 5376 5-simplex ''5-faces'', 4608 6-simplex ''6-faces'', 2304 7-simplex '' ...
or enneacross -
* Demihypercube
In geometry, demihypercubes (also called ''n-demicubes'', ''n-hemicubes'', and ''half measure polytopes'') are a class of ''n''- polytopes constructed from alternation of an ''n''- hypercube, labeled as ''hγn'' for being ''half'' of the hy ...
D9 family: 6,1,1-
** 383 uniform 9-polytope as permutations of rings in the group diagram, including:
**# - 9-demicube or demienneract, 161 - ; also as h .
**# - 9-orthoplex
In geometry, a 9-orthoplex or 9-cross polytope, is a regular 9-polytope with 18 vertices, 144 edges, 672 triangle faces, 2016 tetrahedron cells, 4032 5-cells ''4-faces'', 5376 5-simplex ''5-faces'', 4608 6-simplex ''6-faces'', 2304 7-simplex '' ...
, 611 -
The A9 family
The A9 family has symmetry of order 3628800 (10 factorial). There are 256+16-1=271 forms based on all permutations of the Coxeter-Dynkin diagrams with one or more rings. These are all enumerated below. Bowers-style acronym names are given in parentheses for cross-referencing. {, class="wikitable" !rowspan=2, # !rowspan=2, Graph !rowspan=2, Coxeter-Dynkin diagramSchläfli symbol
In geometry, the Schläfli symbol is a notation of the form \ that defines regular polytopes and tessellations.
The Schläfli symbol is named after the 19th-century Swiss mathematician Ludwig Schläfli, who generalized Euclidean geometry to more ...
Name !colspan=9, Element counts , - , , 8-faces, , 7-faces, , 6-faces, , 5-faces, , 4-faces, , Cells, , Faces, , Edges, , Vertices , - , - align=center !1 ,
t0{3,3,3,3,3,3,3,3}
9-simplex
In geometry, a 9- simplex is a self-dual regular 9-polytope. It has 10 vertices, 45 edges, 120 triangle faces, 210 tetrahedral cells, 252 5-cell 4-faces, 210 5-simplex 5-faces, 120 6-simplex 6-faces, 45 7-simplex 7-faces, and 10 8-simplex 8-fa ...
(day)
, 10, , 45, , 120, , 210, , 252, , 210, , 120, , 45, , 10
, - align=center
!2
, t1{3,3,3,3,3,3,3,3}
Rectified 9-simplex
In nine-dimensional geometry, a rectified 9-simplex is a convex uniform 9-polytope, being a Rectification (geometry), rectification of the regular 9-simplex.
These polytopes are part of a family of 271 uniform 9-polytopes with A9 symmetry.
There ...
(reday)
, , , , , , , , , , , , , , , , 360 , , 45
, - align=center
!3
, t2{3,3,3,3,3,3,3,3}
Birectified 9-simplex (breday) , , , , , , , , , , , , , , , , 1260 , , 120 , - align=center !4 ,
t3{3,3,3,3,3,3,3,3}
Trirectified 9-simplex (treday) , , , , , , , , , , , , , , , , 2520 , , 210 , - align=center BGCOLOR="#e0f0e0" !5 ,
t4{3,3,3,3,3,3,3,3}
Quadrirectified 9-simplex (icoy) , , , , , , , , , , , , , , , , 3150 , , 252 , - align=center !6 ,
t0,1{3,3,3,3,3,3,3,3}
Truncated 9-simplex (teday) , , , , , , , , , , , , , , , , 405 , , 90 , - align=center !7 ,
t0,2{3,3,3,3,3,3,3,3}
Cantellated 9-simplex , , , , , , , , , , , , , , , , 2880 , , 360 , - align=center !8 ,
t1,2{3,3,3,3,3,3,3,3}
Bitruncated 9-simplex , , , , , , , , , , , , , , , , 1620 , , 360 , - align=center !9 ,
t0,3{3,3,3,3,3,3,3,3}
Runcinated 9-simplex , , , , , , , , , , , , , , , , 8820 , , 840 , - align=center !10 ,
t1,3{3,3,3,3,3,3,3,3}
Bicantellated 9-simplex , , , , , , , , , , , , , , , , 10080 , , 1260 , - align=center !11 ,
t2,3{3,3,3,3,3,3,3,3}
Tritruncated 9-simplex (treday) , , , , , , , , , , , , , , , , 3780 , , 840 , - align=center !12 ,
t0,4{3,3,3,3,3,3,3,3}
Stericated 9-simplex , , , , , , , , , , , , , , , , 15120 , , 1260 , - align=center !13 ,
t1,4{3,3,3,3,3,3,3,3}
Biruncinated 9-simplex , , , , , , , , , , , , , , , , 26460 , , 2520 , - align=center !14 ,
t2,4{3,3,3,3,3,3,3,3}
Tricantellated 9-simplex , , , , , , , , , , , , , , , , 20160 , , 2520 , - align=center !15 , ,
t3,4{3,3,3,3,3,3,3,3}
Quadritruncated 9-simplex , , , , , , , , , , , , , , , , 5670 , , 1260 , - align=center !16 ,
t0,5{3,3,3,3,3,3,3,3}
Pentellated 9-simplex , , , , , , , , , , , , , , , , 15750 , , 1260 , - align=center !17 , ,
t1,5{3,3,3,3,3,3,3,3}
Bistericated 9-simplex , , , , , , , , , , , , , , , , 37800 , , 3150 , - align=center !18 , ,
t2,5{3,3,3,3,3,3,3,3}
Triruncinated 9-simplex , , , , , , , , , , , , , , , , 44100 , , 4200 , - align=center BGCOLOR="#e0f0e0" !19 , ,
t3,5{3,3,3,3,3,3,3,3}
Quadricantellated 9-simplex , , , , , , , , , , , , , , , , 25200 , , 3150 , - align=center !20 ,
t0,6{3,3,3,3,3,3,3,3}
Hexicated 9-simplex , , , , , , , , , , , , , , , , 10080 , , 840 , - align=center !21 , ,
t1,6{3,3,3,3,3,3,3,3}
Bipentellated 9-simplex , , , , , , , , , , , , , , , , 31500 , , 2520 , - align=center BGCOLOR="#e0f0e0" !22 , ,
t2,6{3,3,3,3,3,3,3,3}
Tristericated 9-simplex , , , , , , , , , , , , , , , , 50400 , , 4200 , - align=center !23 ,
t0,7{3,3,3,3,3,3,3,3}
Heptellated 9-simplex , , , , , , , , , , , , , , , , 3780 , , 360 , - align=center BGCOLOR="#e0f0e0" !24 , ,
t1,7{3,3,3,3,3,3,3,3}
Bihexicated 9-simplex , , , , , , , , , , , , , , , , 15120 , , 1260 , - align=center BGCOLOR="#e0f0e0" !25 ,
t0,8{3,3,3,3,3,3,3,3}
Octellated 9-simplex , , , , , , , , , , , , , , , , 720 , , 90 , - align=center !26 ,
t0,1,2{3,3,3,3,3,3,3,3}
Cantitruncated 9-simplex , , , , , , , , , , , , , , , , 3240 , , 720 , - align=center !27 , ,
t0,1,3{3,3,3,3,3,3,3,3}
Runcitruncated 9-simplex , , , , , , , , , , , , , , , , 18900 , , 2520 , - align=center !28 , ,
t0,2,3{3,3,3,3,3,3,3,3}
Runcicantellated 9-simplex , , , , , , , , , , , , , , , , 12600 , , 2520 , - align=center !29 ,
t1,2,3{3,3,3,3,3,3,3,3}
Bicantitruncated 9-simplex , , , , , , , , , , , , , , , , 11340 , , 2520 , - align=center !30 , ,
t0,1,4{3,3,3,3,3,3,3,3}
Steritruncated 9-simplex , , , , , , , , , , , , , , , , 47880 , , 5040 , - align=center !31 , ,
t0,2,4{3,3,3,3,3,3,3,3}
Stericantellated 9-simplex , , , , , , , , , , , , , , , , 60480 , , 7560 , - align=center !32 , ,
t1,2,4{3,3,3,3,3,3,3,3}
Biruncitruncated 9-simplex , , , , , , , , , , , , , , , , 52920 , , 7560 , - align=center !33 , ,
t0,3,4{3,3,3,3,3,3,3,3}
Steriruncinated 9-simplex , , , , , , , , , , , , , , , , 27720 , , 5040 , - align=center !34 , ,
t1,3,4{3,3,3,3,3,3,3,3}
Biruncicantellated 9-simplex , , , , , , , , , , , , , , , , 41580 , , 7560 , - align=center !35 ,
t2,3,4{3,3,3,3,3,3,3,3}
Tricantitruncated 9-simplex , , , , , , , , , , , , , , , , 22680 , , 5040 , - align=center !36 , ,
t0,1,5{3,3,3,3,3,3,3,3}
Pentitruncated 9-simplex , , , , , , , , , , , , , , , , 66150 , , 6300 , - align=center !37 , ,
t0,2,5{3,3,3,3,3,3,3,3}
Penticantellated 9-simplex , , , , , , , , , , , , , , , , 126000 , , 12600 , - align=center !38 , ,
t1,2,5{3,3,3,3,3,3,3,3}
Bisteritruncated 9-simplex , , , , , , , , , , , , , , , , 107100 , , 12600 , - align=center !39 , ,
t0,3,5{3,3,3,3,3,3,3,3}
Pentiruncinated 9-simplex , , , , , , , , , , , , , , , , 107100 , , 12600 , - align=center !40 , ,
t1,3,5{3,3,3,3,3,3,3,3}
Bistericantellated 9-simplex , , , , , , , , , , , , , , , , 151200 , , 18900 , - align=center !41 , ,
t2,3,5{3,3,3,3,3,3,3,3}
Triruncitruncated 9-simplex , , , , , , , , , , , , , , , , 81900 , , 12600 , - align=center !42 , ,
t0,4,5{3,3,3,3,3,3,3,3}
Pentistericated 9-simplex , , , , , , , , , , , , , , , , 37800 , , 6300 , - align=center !43 , ,
t1,4,5{3,3,3,3,3,3,3,3}
Bisteriruncinated 9-simplex , , , , , , , , , , , , , , , , 81900 , , 12600 , - align=center !44 , ,
t2,4,5{3,3,3,3,3,3,3,3}
Triruncicantellated 9-simplex , , , , , , , , , , , , , , , , 75600 , , 12600 , - align=center BGCOLOR="#e0f0e0" !45 ,
t3,4,5{3,3,3,3,3,3,3,3}
Quadricantitruncated 9-simplex , , , , , , , , , , , , , , , , 28350 , , 6300 , - align=center !46 , ,
t0,1,6{3,3,3,3,3,3,3,3}
Hexitruncated 9-simplex , , , , , , , , , , , , , , , , 52920 , , 5040 , - align=center !47 , ,
t0,2,6{3,3,3,3,3,3,3,3}
Hexicantellated 9-simplex , , , , , , , , , , , , , , , , 138600 , , 12600 , - align=center !48 , ,
t1,2,6{3,3,3,3,3,3,3,3}
Bipentitruncated 9-simplex , , , , , , , , , , , , , , , , 113400 , , 12600 , - align=center !49 , ,
t0,3,6{3,3,3,3,3,3,3,3}
Hexiruncinated 9-simplex , , , , , , , , , , , , , , , , 176400 , , 16800 , - align=center !50 , ,
t1,3,6{3,3,3,3,3,3,3,3}
Bipenticantellated 9-simplex , , , , , , , , , , , , , , , , 239400 , , 25200 , - align=center !51 , ,
t2,3,6{3,3,3,3,3,3,3,3}
Tristeritruncated 9-simplex , , , , , , , , , , , , , , , , 126000 , , 16800 , - align=center !52 , ,
t0,4,6{3,3,3,3,3,3,3,3}
Hexistericated 9-simplex , , , , , , , , , , , , , , , , 113400 , , 12600 , - align=center !53 , ,
t1,4,6{3,3,3,3,3,3,3,3}
Bipentiruncinated 9-simplex , , , , , , , , , , , , , , , , 226800 , , 25200 , - align=center BGCOLOR="#e0f0e0" !54 , ,
t2,4,6{3,3,3,3,3,3,3,3}
Tristericantellated 9-simplex , , , , , , , , , , , , , , , , 201600 , , 25200 , - align=center !55 , ,
t0,5,6{3,3,3,3,3,3,3,3}
Hexipentellated 9-simplex , , , , , , , , , , , , , , , , 32760 , , 5040 , - align=center !56 , ,
t1,5,6{3,3,3,3,3,3,3,3}
Bipentistericated 9-simplex , , , , , , , , , , , , , , , , 94500 , , 12600 , - align=center !57 , ,
t0,1,7{3,3,3,3,3,3,3,3}
Heptitruncated 9-simplex , , , , , , , , , , , , , , , , 23940 , , 2520 , - align=center !58 , ,
t0,2,7{3,3,3,3,3,3,3,3}
Hepticantellated 9-simplex , , , , , , , , , , , , , , , , 83160 , , 7560 , - align=center !59 , ,
t1,2,7{3,3,3,3,3,3,3,3}
Bihexitruncated 9-simplex , , , , , , , , , , , , , , , , 64260 , , 7560 , - align=center !60 , ,
t0,3,7{3,3,3,3,3,3,3,3}
Heptiruncinated 9-simplex , , , , , , , , , , , , , , , , 144900 , , 12600 , - align=center !61 , ,
t1,3,7{3,3,3,3,3,3,3,3}
Bihexicantellated 9-simplex , , , , , , , , , , , , , , , , 189000 , , 18900 , - align=center !62 , ,
t0,4,7{3,3,3,3,3,3,3,3}
Heptistericated 9-simplex , , , , , , , , , , , , , , , , 138600 , , 12600 , - align=center BGCOLOR="#e0f0e0" !63 , ,
t1,4,7{3,3,3,3,3,3,3,3}
Bihexiruncinated 9-simplex , , , , , , , , , , , , , , , , 264600 , , 25200 , - align=center !64 , ,
t0,5,7{3,3,3,3,3,3,3,3}
Heptipentellated 9-simplex , , , , , , , , , , , , , , , , 71820 , , 7560 , - align=center !65 , ,
t0,6,7{3,3,3,3,3,3,3,3}
Heptihexicated 9-simplex , , , , , , , , , , , , , , , , 17640 , , 2520 , - align=center !66 , ,
t0,1,8{3,3,3,3,3,3,3,3}
Octitruncated 9-simplex , , , , , , , , , , , , , , , , 5400 , , 720 , - align=center !67 , ,
t0,2,8{3,3,3,3,3,3,3,3}
Octicantellated 9-simplex , , , , , , , , , , , , , , , , 25200 , , 2520 , - align=center !68 , ,
t0,3,8{3,3,3,3,3,3,3,3}
Octiruncinated 9-simplex , , , , , , , , , , , , , , , , 57960 , , 5040 , - align=center BGCOLOR="#e0f0e0" !69 , ,
t0,4,8{3,3,3,3,3,3,3,3}
Octistericated 9-simplex , , , , , , , , , , , , , , , , 75600 , , 6300 , - align=center !70 , ,
t0,1,2,3{3,3,3,3,3,3,3,3}
Runcicantitruncated 9-simplex , , , , , , , , , , , , , , , , 22680 , , 5040 , - align=center !71 , ,
t0,1,2,4{3,3,3,3,3,3,3,3}
Stericantitruncated 9-simplex , , , , , , , , , , , , , , , , 105840 , , 15120 , - align=center !72 , ,
t0,1,3,4{3,3,3,3,3,3,3,3}
Steriruncitruncated 9-simplex , , , , , , , , , , , , , , , , 75600 , , 15120 , - align=center !73 , ,
t0,2,3,4{3,3,3,3,3,3,3,3}
Steriruncicantellated 9-simplex , , , , , , , , , , , , , , , , 75600 , , 15120 , - align=center !74 , ,
t1,2,3,4{3,3,3,3,3,3,3,3}
Biruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 68040 , , 15120 , - align=center !75 , ,
t0,1,2,5{3,3,3,3,3,3,3,3}
Penticantitruncated 9-simplex , , , , , , , , , , , , , , , , 214200 , , 25200 , - align=center !76 , ,
t0,1,3,5{3,3,3,3,3,3,3,3}
Pentiruncitruncated 9-simplex , , , , , , , , , , , , , , , , 283500 , , 37800 , - align=center !77 , ,
t0,2,3,5{3,3,3,3,3,3,3,3}
Pentiruncicantellated 9-simplex , , , , , , , , , , , , , , , , 264600 , , 37800 , - align=center !78 , ,
t1,2,3,5{3,3,3,3,3,3,3,3}
Bistericantitruncated 9-simplex , , , , , , , , , , , , , , , , 245700 , , 37800 , - align=center !79 , ,
t0,1,4,5{3,3,3,3,3,3,3,3}
Pentisteritruncated 9-simplex , , , , , , , , , , , , , , , , 138600 , , 25200 , - align=center !80 , ,
t0,2,4,5{3,3,3,3,3,3,3,3}
Pentistericantellated 9-simplex , , , , , , , , , , , , , , , , 226800 , , 37800 , - align=center !81 , ,
t1,2,4,5{3,3,3,3,3,3,3,3}
Bisteriruncitruncated 9-simplex , , , , , , , , , , , , , , , , 189000 , , 37800 , - align=center !82 , ,
t0,3,4,5{3,3,3,3,3,3,3,3}
Pentisteriruncinated 9-simplex , , , , , , , , , , , , , , , , 138600 , , 25200 , - align=center !83 , ,
t1,3,4,5{3,3,3,3,3,3,3,3}
Bisteriruncicantellated 9-simplex , , , , , , , , , , , , , , , , 207900 , , 37800 , - align=center !84 , ,
t2,3,4,5{3,3,3,3,3,3,3,3}
Triruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 113400 , , 25200 , - align=center !85 , ,
t0,1,2,6{3,3,3,3,3,3,3,3}
Hexicantitruncated 9-simplex , , , , , , , , , , , , , , , , 226800 , , 25200 , - align=center !86 , ,
t0,1,3,6{3,3,3,3,3,3,3,3}
Hexiruncitruncated 9-simplex , , , , , , , , , , , , , , , , 453600 , , 50400 , - align=center !87 , ,
t0,2,3,6{3,3,3,3,3,3,3,3}
Hexiruncicantellated 9-simplex , , , , , , , , , , , , , , , , 403200 , , 50400 , - align=center !88 , ,
t1,2,3,6{3,3,3,3,3,3,3,3}
Bipenticantitruncated 9-simplex , , , , , , , , , , , , , , , , 378000 , , 50400 , - align=center !89 , ,
t0,1,4,6{3,3,3,3,3,3,3,3}
Hexisteritruncated 9-simplex , , , , , , , , , , , , , , , , 403200 , , 50400 , - align=center !90 , ,
t0,2,4,6{3,3,3,3,3,3,3,3}
Hexistericantellated 9-simplex , , , , , , , , , , , , , , , , 604800 , , 75600 , - align=center !91 , ,
t1,2,4,6{3,3,3,3,3,3,3,3}
Bipentiruncitruncated 9-simplex , , , , , , , , , , , , , , , , 529200 , , 75600 , - align=center !92 , ,
t0,3,4,6{3,3,3,3,3,3,3,3}
Hexisteriruncinated 9-simplex , , , , , , , , , , , , , , , , 352800 , , 50400 , - align=center !93 , ,
t1,3,4,6{3,3,3,3,3,3,3,3}
Bipentiruncicantellated 9-simplex , , , , , , , , , , , , , , , , 529200 , , 75600 , - align=center !94 , ,
t2,3,4,6{3,3,3,3,3,3,3,3}
Tristericantitruncated 9-simplex , , , , , , , , , , , , , , , , 302400 , , 50400 , - align=center !95 , ,
t0,1,5,6{3,3,3,3,3,3,3,3}
Hexipentitruncated 9-simplex , , , , , , , , , , , , , , , , 151200 , , 25200 , - align=center !96 , ,
t0,2,5,6{3,3,3,3,3,3,3,3}
Hexipenticantellated 9-simplex , , , , , , , , , , , , , , , , 352800 , , 50400 , - align=center !97 , ,
t1,2,5,6{3,3,3,3,3,3,3,3}
Bipentisteritruncated 9-simplex , , , , , , , , , , , , , , , , 277200 , , 50400 , - align=center !98 , ,
t0,3,5,6{3,3,3,3,3,3,3,3}
Hexipentiruncinated 9-simplex , , , , , , , , , , , , , , , , 352800 , , 50400 , - align=center !99 , ,
t1,3,5,6{3,3,3,3,3,3,3,3}
Bipentistericantellated 9-simplex , , , , , , , , , , , , , , , , 491400 , , 75600 , - align=center BGCOLOR="#e0f0e0" !100 , ,
t2,3,5,6{3,3,3,3,3,3,3,3}
Tristeriruncitruncated 9-simplex , , , , , , , , , , , , , , , , 252000 , , 50400 , - align=center !101 , ,
t0,4,5,6{3,3,3,3,3,3,3,3}
Hexipentistericated 9-simplex , , , , , , , , , , , , , , , , 151200 , , 25200 , - align=center !102 , ,
t1,4,5,6{3,3,3,3,3,3,3,3}
Bipentisteriruncinated 9-simplex , , , , , , , , , , , , , , , , 327600 , , 50400 , - align=center !103 , ,
t0,1,2,7{3,3,3,3,3,3,3,3}
Hepticantitruncated 9-simplex , , , , , , , , , , , , , , , , 128520 , , 15120 , - align=center !104 , ,
t0,1,3,7{3,3,3,3,3,3,3,3}
Heptiruncitruncated 9-simplex , , , , , , , , , , , , , , , , 359100 , , 37800 , - align=center !105 , ,
t0,2,3,7{3,3,3,3,3,3,3,3}
Heptiruncicantellated 9-simplex , , , , , , , , , , , , , , , , 302400 , , 37800 , - align=center !106 , ,
t1,2,3,7{3,3,3,3,3,3,3,3}
Bihexicantitruncated 9-simplex , , , , , , , , , , , , , , , , 283500 , , 37800 , - align=center !107 , ,
t0,1,4,7{3,3,3,3,3,3,3,3}
Heptisteritruncated 9-simplex , , , , , , , , , , , , , , , , 478800 , , 50400 , - align=center !108 , ,
t0,2,4,7{3,3,3,3,3,3,3,3}
Heptistericantellated 9-simplex , , , , , , , , , , , , , , , , 680400 , , 75600 , - align=center !109 , ,
t1,2,4,7{3,3,3,3,3,3,3,3}
Bihexiruncitruncated 9-simplex , , , , , , , , , , , , , , , , 604800 , , 75600 , - align=center !110 , ,
t0,3,4,7{3,3,3,3,3,3,3,3}
Heptisteriruncinated 9-simplex , , , , , , , , , , , , , , , , 378000 , , 50400 , - align=center !111 , ,
t1,3,4,7{3,3,3,3,3,3,3,3}
Bihexiruncicantellated 9-simplex , , , , , , , , , , , , , , , , 567000 , , 75600 , - align=center !112 , ,
t0,1,5,7{3,3,3,3,3,3,3,3}
Heptipentitruncated 9-simplex , , , , , , , , , , , , , , , , 321300 , , 37800 , - align=center !113 , ,
t0,2,5,7{3,3,3,3,3,3,3,3}
Heptipenticantellated 9-simplex , , , , , , , , , , , , , , , , 680400 , , 75600 , - align=center !114 , ,
t1,2,5,7{3,3,3,3,3,3,3,3}
Bihexisteritruncated 9-simplex , , , , , , , , , , , , , , , , 567000 , , 75600 , - align=center !115 , ,
t0,3,5,7{3,3,3,3,3,3,3,3}
Heptipentiruncinated 9-simplex , , , , , , , , , , , , , , , , 642600 , , 75600 , - align=center BGCOLOR="#e0f0e0" !116 , ,
t1,3,5,7{3,3,3,3,3,3,3,3}
Bihexistericantellated 9-simplex , , , , , , , , , , , , , , , , 907200 , , 113400 , - align=center !117 , ,
t0,4,5,7{3,3,3,3,3,3,3,3}
Heptipentistericated 9-simplex , , , , , , , , , , , , , , , , 264600 , , 37800 , - align=center !118 , ,
t0,1,6,7{3,3,3,3,3,3,3,3}
Heptihexitruncated 9-simplex , , , , , , , , , , , , , , , , 98280 , , 15120 , - align=center !119 , ,
t0,2,6,7{3,3,3,3,3,3,3,3}
Heptihexicantellated 9-simplex , , , , , , , , , , , , , , , , 302400 , , 37800 , - align=center BGCOLOR="#e0f0e0" !120 , ,
t1,2,6,7{3,3,3,3,3,3,3,3}
Bihexipentitruncated 9-simplex , , , , , , , , , , , , , , , , 226800 , , 37800 , - align=center !121 , ,
t0,3,6,7{3,3,3,3,3,3,3,3}
Heptihexiruncinated 9-simplex , , , , , , , , , , , , , , , , 428400 , , 50400 , - align=center !122 , ,
t0,4,6,7{3,3,3,3,3,3,3,3}
Heptihexistericated 9-simplex , , , , , , , , , , , , , , , , 302400 , , 37800 , - align=center !123 , ,
t0,5,6,7{3,3,3,3,3,3,3,3}
Heptihexipentellated 9-simplex , , , , , , , , , , , , , , , , 98280 , , 15120 , - align=center !124 , ,
t0,1,2,8{3,3,3,3,3,3,3,3}
Octicantitruncated 9-simplex , , , , , , , , , , , , , , , , 35280 , , 5040 , - align=center !125 , ,
t0,1,3,8{3,3,3,3,3,3,3,3}
Octiruncitruncated 9-simplex , , , , , , , , , , , , , , , , 136080 , , 15120 , - align=center !126 , ,
t0,2,3,8{3,3,3,3,3,3,3,3}
Octiruncicantellated 9-simplex , , , , , , , , , , , , , , , , 105840 , , 15120 , - align=center !127 , ,
t0,1,4,8{3,3,3,3,3,3,3,3}
Octisteritruncated 9-simplex , , , , , , , , , , , , , , , , 252000 , , 25200 , - align=center !128 , ,
t0,2,4,8{3,3,3,3,3,3,3,3}
Octistericantellated 9-simplex , , , , , , , , , , , , , , , , 340200 , , 37800 , - align=center !129 , ,
t0,3,4,8{3,3,3,3,3,3,3,3}
Octisteriruncinated 9-simplex , , , , , , , , , , , , , , , , 176400 , , 25200 , - align=center !130 , ,
t0,1,5,8{3,3,3,3,3,3,3,3}
Octipentitruncated 9-simplex , , , , , , , , , , , , , , , , 252000 , , 25200 , - align=center !131 , ,
t0,2,5,8{3,3,3,3,3,3,3,3}
Octipenticantellated 9-simplex , , , , , , , , , , , , , , , , 504000 , , 50400 , - align=center BGCOLOR="#e0f0e0" !132 , ,
t0,3,5,8{3,3,3,3,3,3,3,3}
Octipentiruncinated 9-simplex , , , , , , , , , , , , , , , , 453600 , , 50400 , - align=center !133 , ,
t0,1,6,8{3,3,3,3,3,3,3,3}
Octihexitruncated 9-simplex , , , , , , , , , , , , , , , , 136080 , , 15120 , - align=center BGCOLOR="#e0f0e0" !134 , ,
t0,2,6,8{3,3,3,3,3,3,3,3}
Octihexicantellated 9-simplex , , , , , , , , , , , , , , , , 378000 , , 37800 , - align=center BGCOLOR="#e0f0e0" !135 , ,
t0,1,7,8{3,3,3,3,3,3,3,3}
Octiheptitruncated 9-simplex , , , , , , , , , , , , , , , , 35280 , , 5040 , - align=center !136 , ,
t0,1,2,3,4{3,3,3,3,3,3,3,3}
Steriruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 136080 , , 30240 , - align=center !137 , ,
t0,1,2,3,5{3,3,3,3,3,3,3,3}
Pentiruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 491400 , , 75600 , - align=center !138 , ,
t0,1,2,4,5{3,3,3,3,3,3,3,3}
Pentistericantitruncated 9-simplex , , , , , , , , , , , , , , , , 378000 , , 75600 , - align=center !139 , ,
t0,1,3,4,5{3,3,3,3,3,3,3,3}
Pentisteriruncitruncated 9-simplex , , , , , , , , , , , , , , , , 378000 , , 75600 , - align=center !140 , ,
t0,2,3,4,5{3,3,3,3,3,3,3,3}
Pentisteriruncicantellated 9-simplex , , , , , , , , , , , , , , , , 378000 , , 75600 , - align=center !141 , ,
t1,2,3,4,5{3,3,3,3,3,3,3,3}
Bisteriruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 340200 , , 75600 , - align=center !142 , ,
t0,1,2,3,6{3,3,3,3,3,3,3,3}
Hexiruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 756000 , , 100800 , - align=center !143 , ,
t0,1,2,4,6{3,3,3,3,3,3,3,3}
Hexistericantitruncated 9-simplex , , , , , , , , , , , , , , , , 1058400 , , 151200 , - align=center !144 , ,
t0,1,3,4,6{3,3,3,3,3,3,3,3}
Hexisteriruncitruncated 9-simplex , , , , , , , , , , , , , , , , 982800 , , 151200 , - align=center !145 , ,
t0,2,3,4,6{3,3,3,3,3,3,3,3}
Hexisteriruncicantellated 9-simplex , , , , , , , , , , , , , , , , 982800 , , 151200 , - align=center !146 , ,
t1,2,3,4,6{3,3,3,3,3,3,3,3}
Bipentiruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 907200 , , 151200 , - align=center !147 , ,
t0,1,2,5,6{3,3,3,3,3,3,3,3}
Hexipenticantitruncated 9-simplex , , , , , , , , , , , , , , , , 554400 , , 100800 , - align=center !148 , ,
t0,1,3,5,6{3,3,3,3,3,3,3,3}
Hexipentiruncitruncated 9-simplex , , , , , , , , , , , , , , , , 907200 , , 151200 , - align=center !149 , ,
t0,2,3,5,6{3,3,3,3,3,3,3,3}
Hexipentiruncicantellated 9-simplex , , , , , , , , , , , , , , , , 831600 , , 151200 , - align=center !150 , ,
t1,2,3,5,6{3,3,3,3,3,3,3,3}
Bipentistericantitruncated 9-simplex , , , , , , , , , , , , , , , , 756000 , , 151200 , - align=center !151 , ,
t0,1,4,5,6{3,3,3,3,3,3,3,3}
Hexipentisteritruncated 9-simplex , , , , , , , , , , , , , , , , 554400 , , 100800 , - align=center !152 , ,
t0,2,4,5,6{3,3,3,3,3,3,3,3}
Hexipentistericantellated 9-simplex , , , , , , , , , , , , , , , , 907200 , , 151200 , - align=center !153 , ,
t1,2,4,5,6{3,3,3,3,3,3,3,3}
Bipentisteriruncitruncated 9-simplex , , , , , , , , , , , , , , , , 756000 , , 151200 , - align=center !154 , ,
t0,3,4,5,6{3,3,3,3,3,3,3,3}
Hexipentisteriruncinated 9-simplex , , , , , , , , , , , , , , , , 554400 , , 100800 , - align=center !155 , ,
t1,3,4,5,6{3,3,3,3,3,3,3,3}
Bipentisteriruncicantellated 9-simplex , , , , , , , , , , , , , , , , 831600 , , 151200 , - align=center BGCOLOR="#e0f0e0" !156 , ,
t2,3,4,5,6{3,3,3,3,3,3,3,3}
Tristeriruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 453600 , , 100800 , - align=center !157 , ,
t0,1,2,3,7{3,3,3,3,3,3,3,3}
Heptiruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 567000 , , 75600 , - align=center !158 , ,
t0,1,2,4,7{3,3,3,3,3,3,3,3}
Heptistericantitruncated 9-simplex , , , , , , , , , , , , , , , , 1209600 , , 151200 , - align=center !159 , ,
t0,1,3,4,7{3,3,3,3,3,3,3,3}
Heptisteriruncitruncated 9-simplex , , , , , , , , , , , , , , , , 1058400 , , 151200 , - align=center !160 , ,
t0,2,3,4,7{3,3,3,3,3,3,3,3}
Heptisteriruncicantellated 9-simplex , , , , , , , , , , , , , , , , 1058400 , , 151200 , - align=center !161 , ,
t1,2,3,4,7{3,3,3,3,3,3,3,3}
Bihexiruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 982800 , , 151200 , - align=center !162 , ,
t0,1,2,5,7{3,3,3,3,3,3,3,3}
Heptipenticantitruncated 9-simplex , , , , , , , , , , , , , , , , 1134000 , , 151200 , - align=center !163 , ,
t0,1,3,5,7{3,3,3,3,3,3,3,3}
Heptipentiruncitruncated 9-simplex , , , , , , , , , , , , , , , , 1701000 , , 226800 , - align=center !164 , ,
t0,2,3,5,7{3,3,3,3,3,3,3,3}
Heptipentiruncicantellated 9-simplex , , , , , , , , , , , , , , , , 1587600 , , 226800 , - align=center !165 , ,
t1,2,3,5,7{3,3,3,3,3,3,3,3}
Bihexistericantitruncated 9-simplex , , , , , , , , , , , , , , , , 1474200 , , 226800 , - align=center !166 , ,
t0,1,4,5,7{3,3,3,3,3,3,3,3}
Heptipentisteritruncated 9-simplex , , , , , , , , , , , , , , , , 982800 , , 151200 , - align=center !167 , ,
t0,2,4,5,7{3,3,3,3,3,3,3,3}
Heptipentistericantellated 9-simplex , , , , , , , , , , , , , , , , 1587600 , , 226800 , - align=center !168 , ,
t1,2,4,5,7{3,3,3,3,3,3,3,3}
Bihexisteriruncitruncated 9-simplex , , , , , , , , , , , , , , , , 1360800 , , 226800 , - align=center !169 , ,
t0,3,4,5,7{3,3,3,3,3,3,3,3}
Heptipentisteriruncinated 9-simplex , , , , , , , , , , , , , , , , 982800 , , 151200 , - align=center BGCOLOR="#e0f0e0" !170 , ,
t1,3,4,5,7{3,3,3,3,3,3,3,3}
Bihexisteriruncicantellated 9-simplex , , , , , , , , , , , , , , , , 1474200 , , 226800 , - align=center !171 , ,
t0,1,2,6,7{3,3,3,3,3,3,3,3}
Heptihexicantitruncated 9-simplex , , , , , , , , , , , , , , , , 453600 , , 75600 , - align=center !172 , ,
t0,1,3,6,7{3,3,3,3,3,3,3,3}
Heptihexiruncitruncated 9-simplex , , , , , , , , , , , , , , , , 1058400 , , 151200 , - align=center !173 , ,
t0,2,3,6,7{3,3,3,3,3,3,3,3}
Heptihexiruncicantellated 9-simplex , , , , , , , , , , , , , , , , 907200 , , 151200 , - align=center !174 , ,
t1,2,3,6,7{3,3,3,3,3,3,3,3}
Bihexipenticantitruncated 9-simplex , , , , , , , , , , , , , , , , 831600 , , 151200 , - align=center !175 , ,
t0,1,4,6,7{3,3,3,3,3,3,3,3}
Heptihexisteritruncated 9-simplex , , , , , , , , , , , , , , , , 1058400 , , 151200 , - align=center !176 , ,
t0,2,4,6,7{3,3,3,3,3,3,3,3}
Heptihexistericantellated 9-simplex , , , , , , , , , , , , , , , , 1587600 , , 226800 , - align=center BGCOLOR="#e0f0e0" !177 , ,
t1,2,4,6,7{3,3,3,3,3,3,3,3}
Bihexipentiruncitruncated 9-simplex , , , , , , , , , , , , , , , , 1360800 , , 226800 , - align=center !178 , ,
t0,3,4,6,7{3,3,3,3,3,3,3,3}
Heptihexisteriruncinated 9-simplex , , , , , , , , , , , , , , , , 907200 , , 151200 , - align=center !179 , ,
t0,1,5,6,7{3,3,3,3,3,3,3,3}
Heptihexipentitruncated 9-simplex , , , , , , , , , , , , , , , , 453600 , , 75600 , - align=center !180 , ,
t0,2,5,6,7{3,3,3,3,3,3,3,3}
Heptihexipenticantellated 9-simplex , , , , , , , , , , , , , , , , 1058400 , , 151200 , - align=center !181 , ,
t0,3,5,6,7{3,3,3,3,3,3,3,3}
Heptihexipentiruncinated 9-simplex , , , , , , , , , , , , , , , , 1058400 , , 151200 , - align=center !182 , ,
t0,4,5,6,7{3,3,3,3,3,3,3,3}
Heptihexipentistericated 9-simplex , , , , , , , , , , , , , , , , 453600 , , 75600 , - align=center !183 , ,
t0,1,2,3,8{3,3,3,3,3,3,3,3}
Octiruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 196560 , , 30240 , - align=center !184 , ,
t0,1,2,4,8{3,3,3,3,3,3,3,3}
Octistericantitruncated 9-simplex , , , , , , , , , , , , , , , , 604800 , , 75600 , - align=center !185 , ,
t0,1,3,4,8{3,3,3,3,3,3,3,3}
Octisteriruncitruncated 9-simplex , , , , , , , , , , , , , , , , 491400 , , 75600 , - align=center !186 , ,
t0,2,3,4,8{3,3,3,3,3,3,3,3}
Octisteriruncicantellated 9-simplex , , , , , , , , , , , , , , , , 491400 , , 75600 , - align=center !187 , ,
t0,1,2,5,8{3,3,3,3,3,3,3,3}
Octipenticantitruncated 9-simplex , , , , , , , , , , , , , , , , 856800 , , 100800 , - align=center !188 , ,
t0,1,3,5,8{3,3,3,3,3,3,3,3}
Octipentiruncitruncated 9-simplex , , , , , , , , , , , , , , , , 1209600 , , 151200 , - align=center !189 , ,
t0,2,3,5,8{3,3,3,3,3,3,3,3}
Octipentiruncicantellated 9-simplex , , , , , , , , , , , , , , , , 1134000 , , 151200 , - align=center !190 , ,
t0,1,4,5,8{3,3,3,3,3,3,3,3}
Octipentisteritruncated 9-simplex , , , , , , , , , , , , , , , , 655200 , , 100800 , - align=center !191 , ,
t0,2,4,5,8{3,3,3,3,3,3,3,3}
Octipentistericantellated 9-simplex , , , , , , , , , , , , , , , , 1058400 , , 151200 , - align=center BGCOLOR="#e0f0e0" !192 , ,
t0,3,4,5,8{3,3,3,3,3,3,3,3}
Octipentisteriruncinated 9-simplex , , , , , , , , , , , , , , , , 655200 , , 100800 , - align=center !193 , ,
t0,1,2,6,8{3,3,3,3,3,3,3,3}
Octihexicantitruncated 9-simplex , , , , , , , , , , , , , , , , 604800 , , 75600 , - align=center !194 , ,
t0,1,3,6,8{3,3,3,3,3,3,3,3}
Octihexiruncitruncated 9-simplex , , , , , , , , , , , , , , , , 1285200 , , 151200 , - align=center !195 , ,
t0,2,3,6,8{3,3,3,3,3,3,3,3}
Octihexiruncicantellated 9-simplex , , , , , , , , , , , , , , , , 1134000 , , 151200 , - align=center !196 , ,
t0,1,4,6,8{3,3,3,3,3,3,3,3}
Octihexisteritruncated 9-simplex , , , , , , , , , , , , , , , , 1209600 , , 151200 , - align=center BGCOLOR="#e0f0e0" !197 , ,
t0,2,4,6,8{3,3,3,3,3,3,3,3}
Octihexistericantellated 9-simplex , , , , , , , , , , , , , , , , 1814400 , , 226800 , - align=center !198 , ,
t0,1,5,6,8{3,3,3,3,3,3,3,3}
Octihexipentitruncated 9-simplex , , , , , , , , , , , , , , , , 491400 , , 75600 , - align=center !199 , ,
t0,1,2,7,8{3,3,3,3,3,3,3,3}
Octihepticantitruncated 9-simplex , , , , , , , , , , , , , , , , 196560 , , 30240 , - align=center !200 , ,
t0,1,3,7,8{3,3,3,3,3,3,3,3}
Octiheptiruncitruncated 9-simplex , , , , , , , , , , , , , , , , 604800 , , 75600 , - align=center BGCOLOR="#e0f0e0" !201 , ,
t0,1,4,7,8{3,3,3,3,3,3,3,3}
Octiheptisteritruncated 9-simplex , , , , , , , , , , , , , , , , 856800 , , 100800 , - align=center !202 , ,
t0,1,2,3,4,5{3,3,3,3,3,3,3,3}
Pentisteriruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 680400 , , 151200 , - align=center !203 , ,
t0,1,2,3,4,6{3,3,3,3,3,3,3,3}
Hexisteriruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 1814400 , , 302400 , - align=center !204 , ,
t0,1,2,3,5,6{3,3,3,3,3,3,3,3}
Hexipentiruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 1512000 , , 302400 , - align=center !205 , ,
t0,1,2,4,5,6{3,3,3,3,3,3,3,3}
Hexipentistericantitruncated 9-simplex , , , , , , , , , , , , , , , , 1512000 , , 302400 , - align=center !206 , ,
t0,1,3,4,5,6{3,3,3,3,3,3,3,3}
Hexipentisteriruncitruncated 9-simplex , , , , , , , , , , , , , , , , 1512000 , , 302400 , - align=center !207 , ,
t0,2,3,4,5,6{3,3,3,3,3,3,3,3}
Hexipentisteriruncicantellated 9-simplex , , , , , , , , , , , , , , , , 1512000 , , 302400 , - align=center !208 , ,
t1,2,3,4,5,6{3,3,3,3,3,3,3,3}
Bipentisteriruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 1360800 , , 302400 , - align=center !209 , ,
t0,1,2,3,4,7{3,3,3,3,3,3,3,3}
Heptisteriruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 1965600 , , 302400 , - align=center !210 , ,
t0,1,2,3,5,7{3,3,3,3,3,3,3,3}
Heptipentiruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 2948400 , , 453600 , - align=center !211 , ,
t0,1,2,4,5,7{3,3,3,3,3,3,3,3}
Heptipentistericantitruncated 9-simplex , , , , , , , , , , , , , , , , 2721600 , , 453600 , - align=center !212 , ,
t0,1,3,4,5,7{3,3,3,3,3,3,3,3}
Heptipentisteriruncitruncated 9-simplex , , , , , , , , , , , , , , , , 2721600 , , 453600 , - align=center !213 , ,
t0,2,3,4,5,7{3,3,3,3,3,3,3,3}
Heptipentisteriruncicantellated 9-simplex , , , , , , , , , , , , , , , , 2721600 , , 453600 , - align=center !214 , ,
t1,2,3,4,5,7{3,3,3,3,3,3,3,3}
Bihexisteriruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 2494800 , , 453600 , - align=center !215 , ,
t0,1,2,3,6,7{3,3,3,3,3,3,3,3}
Heptihexiruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 1663200 , , 302400 , - align=center !216 , ,
t0,1,2,4,6,7{3,3,3,3,3,3,3,3}
Heptihexistericantitruncated 9-simplex , , , , , , , , , , , , , , , , 2721600 , , 453600 , - align=center !217 , ,
t0,1,3,4,6,7{3,3,3,3,3,3,3,3}
Heptihexisteriruncitruncated 9-simplex , , , , , , , , , , , , , , , , 2494800 , , 453600 , - align=center !218 , ,
t0,2,3,4,6,7{3,3,3,3,3,3,3,3}
Heptihexisteriruncicantellated 9-simplex , , , , , , , , , , , , , , , , 2494800 , , 453600 , - align=center !219 , ,
t1,2,3,4,6,7{3,3,3,3,3,3,3,3}
Bihexipentiruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 2268000 , , 453600 , - align=center !220 , ,
t0,1,2,5,6,7{3,3,3,3,3,3,3,3}
Heptihexipenticantitruncated 9-simplex , , , , , , , , , , , , , , , , 1663200 , , 302400 , - align=center !221 , ,
t0,1,3,5,6,7{3,3,3,3,3,3,3,3}
Heptihexipentiruncitruncated 9-simplex , , , , , , , , , , , , , , , , 2721600 , , 453600 , - align=center !222 , ,
t0,2,3,5,6,7{3,3,3,3,3,3,3,3}
Heptihexipentiruncicantellated 9-simplex , , , , , , , , , , , , , , , , 2494800 , , 453600 , - align=center BGCOLOR="#e0f0e0" !223 , ,
t1,2,3,5,6,7{3,3,3,3,3,3,3,3}
Bihexipentistericantitruncated 9-simplex , , , , , , , , , , , , , , , , 2268000 , , 453600 , - align=center !224 , ,
t0,1,4,5,6,7{3,3,3,3,3,3,3,3}
Heptihexipentisteritruncated 9-simplex , , , , , , , , , , , , , , , , 1663200 , , 302400 , - align=center !225 , ,
t0,2,4,5,6,7{3,3,3,3,3,3,3,3}
Heptihexipentistericantellated 9-simplex , , , , , , , , , , , , , , , , 2721600 , , 453600 , - align=center !226 , ,
t0,3,4,5,6,7{3,3,3,3,3,3,3,3}
Heptihexipentisteriruncinated 9-simplex , , , , , , , , , , , , , , , , 1663200 , , 302400 , - align=center !227 , ,
t0,1,2,3,4,8{3,3,3,3,3,3,3,3}
Octisteriruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 907200 , , 151200 , - align=center !228 , ,
t0,1,2,3,5,8{3,3,3,3,3,3,3,3}
Octipentiruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 2116800 , , 302400 , - align=center !229 , ,
t0,1,2,4,5,8{3,3,3,3,3,3,3,3}
Octipentistericantitruncated 9-simplex , , , , , , , , , , , , , , , , 1814400 , , 302400 , - align=center !230 , ,
t0,1,3,4,5,8{3,3,3,3,3,3,3,3}
Octipentisteriruncitruncated 9-simplex , , , , , , , , , , , , , , , , 1814400 , , 302400 , - align=center !231 , ,
t0,2,3,4,5,8{3,3,3,3,3,3,3,3}
Octipentisteriruncicantellated 9-simplex , , , , , , , , , , , , , , , , 1814400 , , 302400 , - align=center !232 , ,
t0,1,2,3,6,8{3,3,3,3,3,3,3,3}
Octihexiruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 2116800 , , 302400 , - align=center !233 , ,
t0,1,2,4,6,8{3,3,3,3,3,3,3,3}
Octihexistericantitruncated 9-simplex , , , , , , , , , , , , , , , , 3175200 , , 453600 , - align=center !234 , ,
t0,1,3,4,6,8{3,3,3,3,3,3,3,3}
Octihexisteriruncitruncated 9-simplex , , , , , , , , , , , , , , , , 2948400 , , 453600 , - align=center !235 , ,
t0,2,3,4,6,8{3,3,3,3,3,3,3,3}
Octihexisteriruncicantellated 9-simplex , , , , , , , , , , , , , , , , 2948400 , , 453600 , - align=center !236 , ,
t0,1,2,5,6,8{3,3,3,3,3,3,3,3}
Octihexipenticantitruncated 9-simplex , , , , , , , , , , , , , , , , 1814400 , , 302400 , - align=center !237 , ,
t0,1,3,5,6,8{3,3,3,3,3,3,3,3}
Octihexipentiruncitruncated 9-simplex , , , , , , , , , , , , , , , , 2948400 , , 453600 , - align=center BGCOLOR="#e0f0e0" !238 , ,
t0,2,3,5,6,8{3,3,3,3,3,3,3,3}
Octihexipentiruncicantellated 9-simplex , , , , , , , , , , , , , , , , 2721600 , , 453600 , - align=center !239 , ,
t0,1,4,5,6,8{3,3,3,3,3,3,3,3}
Octihexipentisteritruncated 9-simplex , , , , , , , , , , , , , , , , 1814400 , , 302400 , - align=center !240 , ,
t0,1,2,3,7,8{3,3,3,3,3,3,3,3}
Octiheptiruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 907200 , , 151200 , - align=center !241 , ,
t0,1,2,4,7,8{3,3,3,3,3,3,3,3}
Octiheptistericantitruncated 9-simplex , , , , , , , , , , , , , , , , 2116800 , , 302400 , - align=center !242 , ,
t0,1,3,4,7,8{3,3,3,3,3,3,3,3}
Octiheptisteriruncitruncated 9-simplex , , , , , , , , , , , , , , , , 1814400 , , 302400 , - align=center !243 , ,
t0,1,2,5,7,8{3,3,3,3,3,3,3,3}
Octiheptipenticantitruncated 9-simplex , , , , , , , , , , , , , , , , 2116800 , , 302400 , - align=center BGCOLOR="#e0f0e0" !244 , ,
t0,1,3,5,7,8{3,3,3,3,3,3,3,3}
Octiheptipentiruncitruncated 9-simplex , , , , , , , , , , , , , , , , 3175200 , , 453600 , - align=center BGCOLOR="#e0f0e0" !245 , ,
t0,1,2,6,7,8{3,3,3,3,3,3,3,3}
Octiheptihexicantitruncated 9-simplex , , , , , , , , , , , , , , , , 907200 , , 151200 , - align=center !246 , ,
t0,1,2,3,4,5,6{3,3,3,3,3,3,3,3}
Hexipentisteriruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 2721600 , , 604800 , - align=center !247 , ,
t0,1,2,3,4,5,7{3,3,3,3,3,3,3,3}
Heptipentisteriruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 4989600 , , 907200 , - align=center !248 , ,
t0,1,2,3,4,6,7{3,3,3,3,3,3,3,3}
Heptihexisteriruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 4536000 , , 907200 , - align=center !249 , ,
t0,1,2,3,5,6,7{3,3,3,3,3,3,3,3}
Heptihexipentiruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 4536000 , , 907200 , - align=center !250 , ,
t0,1,2,4,5,6,7{3,3,3,3,3,3,3,3}
Heptihexipentistericantitruncated 9-simplex , , , , , , , , , , , , , , , , 4536000 , , 907200 , - align=center !251 , ,
t0,1,3,4,5,6,7{3,3,3,3,3,3,3,3}
Heptihexipentisteriruncitruncated 9-simplex , , , , , , , , , , , , , , , , 4536000 , , 907200 , - align=center !252 , ,
t0,2,3,4,5,6,7{3,3,3,3,3,3,3,3}
Heptihexipentisteriruncicantellated 9-simplex , , , , , , , , , , , , , , , , 4536000 , , 907200 , - align=center BGCOLOR="#e0f0e0" !253 , ,
t1,2,3,4,5,6,7{3,3,3,3,3,3,3,3}
Bihexipentisteriruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 4082400 , , 907200 , - align=center !254 , ,
t0,1,2,3,4,5,8{3,3,3,3,3,3,3,3}
Octipentisteriruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 3326400 , , 604800 , - align=center !255 , ,
t0,1,2,3,4,6,8{3,3,3,3,3,3,3,3}
Octihexisteriruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 5443200 , , 907200 , - align=center !256 , ,
t0,1,2,3,5,6,8{3,3,3,3,3,3,3,3}
Octihexipentiruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 4989600 , , 907200 , - align=center !257 , ,
t0,1,2,4,5,6,8{3,3,3,3,3,3,3,3}
Octihexipentistericantitruncated 9-simplex , , , , , , , , , , , , , , , , 4989600 , , 907200 , - align=center !258 , ,
t0,1,3,4,5,6,8{3,3,3,3,3,3,3,3}
Octihexipentisteriruncitruncated 9-simplex , , , , , , , , , , , , , , , , 4989600 , , 907200 , - align=center BGCOLOR="#e0f0e0" !259 , ,
t0,2,3,4,5,6,8{3,3,3,3,3,3,3,3}
Octihexipentisteriruncicantellated 9-simplex , , , , , , , , , , , , , , , , 4989600 , , 907200 , - align=center !260 , ,
t0,1,2,3,4,7,8{3,3,3,3,3,3,3,3}
Octiheptisteriruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 3326400 , , 604800 , - align=center !261 , ,
t0,1,2,3,5,7,8{3,3,3,3,3,3,3,3}
Octiheptipentiruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 5443200 , , 907200 , - align=center !262 , ,
t0,1,2,4,5,7,8{3,3,3,3,3,3,3,3}
Octiheptipentistericantitruncated 9-simplex , , , , , , , , , , , , , , , , 4989600 , , 907200 , - align=center BGCOLOR="#e0f0e0" !263 , ,
t0,1,3,4,5,7,8{3,3,3,3,3,3,3,3}
Octiheptipentisteriruncitruncated 9-simplex , , , , , , , , , , , , , , , , 4989600 , , 907200 , - align=center !264 , ,
t0,1,2,3,6,7,8{3,3,3,3,3,3,3,3}
Octiheptihexiruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 3326400 , , 604800 , - align=center BGCOLOR="#e0f0e0" !265 , ,
t0,1,2,4,6,7,8{3,3,3,3,3,3,3,3}
Octiheptihexistericantitruncated 9-simplex , , , , , , , , , , , , , , , , 5443200 , , 907200 , - align=center !266 , ,
t0,1,2,3,4,5,6,7{3,3,3,3,3,3,3,3}
Heptihexipentisteriruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 8164800 , , 1814400 , - align=center !267 , ,
t0,1,2,3,4,5,6,8{3,3,3,3,3,3,3,3}
Octihexipentisteriruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 9072000 , , 1814400 , - align=center !268 , ,
t0,1,2,3,4,5,7,8{3,3,3,3,3,3,3,3}
Octiheptipentisteriruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 9072000 , , 1814400 , - align=center !269 , ,
t0,1,2,3,4,6,7,8{3,3,3,3,3,3,3,3}
Octiheptihexisteriruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 9072000 , , 1814400 , - align=center BGCOLOR="#e0f0e0" !270 , ,
t0,1,2,3,5,6,7,8{3,3,3,3,3,3,3,3}
Octiheptihexipentiruncicantitruncated 9-simplex , , , , , , , , , , , , , , , , 9072000 , , 1814400 , - align=center BGCOLOR="#e0f0e0" !271 , ,
t0,1,2,3,4,5,6,7,8{3,3,3,3,3,3,3,3}
Omnitruncated 9-simplex , , , , , , , , , , , , , , , , 16329600 , , 3628800
The B9 family
There are 511 forms based on all permutations of the Coxeter-Dynkin diagrams with one or more rings. Eleven cases are shown below: Nine rectified forms and 2 truncations. Bowers-style acronym names are given in parentheses for cross-referencing. Bowers-style acronym names are given in parentheses for cross-referencing. {, class="wikitable" !rowspan=2, # !rowspan=2, Graph !rowspan=2, Coxeter-Dynkin diagramSchläfli symbol
In geometry, the Schläfli symbol is a notation of the form \ that defines regular polytopes and tessellations.
The Schläfli symbol is named after the 19th-century Swiss mathematician Ludwig Schläfli, who generalized Euclidean geometry to more ...
Name !colspan=10, Element counts , - ! 8-faces ! 7-faces ! 6-faces ! 5-faces ! 4-faces ! Cells ! Faces ! Edges ! Vertices , - align=center !1 ,
t0{4,3,3,3,3,3,3,3}
9-cube
In geometry, a 9-cube is a nine-dimensional hypercube with 512 vertices, 2304 edges, 4608 square faces, 5376 cubic cells, 4032 tesseract 4-faces, 2016 5-cube 5-faces, 672 6-cube 6-faces, 144 7-cube 7-faces, and 18 8-cube 8-faces.
It can be ...
(enne)
, 18, , 144, , 672, , 2016, , 4032, , 5376, , 4608, , 2304, , 512
, - align=center
!2
,  ,
, t0,1{4,3,3,3,3,3,3,3}
Truncated 9-cube (ten) , , , , , , , , , , , , , , , , 2304 , , 4608 , - align=center !3 ,
 ,
, t1{4,3,3,3,3,3,3,3}
Rectified 9-cube (ren) , , , , , , , , , , , , , , , , 18432 , , 2304 , - align=center !4 ,
 ,
, t2{4,3,3,3,3,3,3,3}
Birectified 9-cube (barn) , , , , , , , , , , , , , , , , 64512 , , 4608 , - align=center !5 ,
 ,
, t3{4,3,3,3,3,3,3,3}
Trirectified 9-cube (tarn) , , , , , , , , , , , , , , , , 96768 , , 5376 , - align=center !6 ,
 ,
, t4{4,3,3,3,3,3,3,3}
Quadrirectified 9-cube (nav)
(Quadrirectified 9-orthoplex) , , , , , , , , , , , , , , , , 80640, , 4032 , - align=center !7 ,
 ,
, t3{3,3,3,3,3,3,3,4}
Trirectified 9-orthoplex (tarv) , , , , , , , , , , , , , , , , 40320 , , 2016 , - align=center !8 ,
 ,
, t2{3,3,3,3,3,3,3,4}
Birectified 9-orthoplex (brav) , , , , , , , , , , , , , , , , 12096 , , 672 , - align=center !9 ,
 ,
, t1{3,3,3,3,3,3,3,4}
Rectified 9-orthoplex (riv) , , , , , , , , , , , , , , , 2016 , , 144 , - align=center !10 ,
 ,
, t0,1{3,3,3,3,3,3,3,4}
Truncated 9-orthoplex (tiv) , , , , , , , , , , , , , , , 2160 , , 288 , - align=center !11 ,
 ,
, t0{3,3,3,3,3,3,3,4}
9-orthoplex
In geometry, a 9-orthoplex or 9-cross polytope, is a regular 9-polytope with 18 vertices, 144 edges, 672 triangle faces, 2016 tetrahedron cells, 4032 5-cells ''4-faces'', 5376 5-simplex ''5-faces'', 4608 6-simplex ''6-faces'', 2304 7-simplex '' ...
(vee)
, 512, , 2304, , 4608, , 5376, , 4032, , 2016, , 672, , 144, , 18
The D9 family
The D9 family has symmetry of order 92,897,280 (9factorial
In mathematics, the factorial of a non-negative denoted is the product of all positive integers less than or equal The factorial also equals the product of n with the next smaller factorial:
\begin
n! &= n \times (n-1) \times (n-2) \t ...
× 28).
This family has 3×128−1=383 Wythoffian uniform polytopes, generated by marking one or more nodes of the D9 Coxeter-Dynkin diagram. Of these, 255 (2×128−1) are repeated from the B9 family and 128 are unique to this family, with the eight 1 or 2 ringed forms listed below. Bowers-style acronym names are given in parentheses for cross-referencing.
{, class="wikitable"
!rowspan=2, #
!colspan=11, Coxeter plane
In mathematics, the Coxeter number ''h'' is the order of a Coxeter element of an irreducible Coxeter group. It is named after H.S.M. Coxeter.
Definitions
Note that this article assumes a finite Coxeter group. For infinite Coxeter groups, there a ...
graphs
!rowspan=2, Coxeter-Dynkin diagramSchläfli symbol
In geometry, the Schläfli symbol is a notation of the form \ that defines regular polytopes and tessellations.
The Schläfli symbol is named after the 19th-century Swiss mathematician Ludwig Schläfli, who generalized Euclidean geometry to more ...
!rowspan=2, Base point(Alternately signed) !colspan=9, Element counts !rowspan=2, Circumrad , - ! B9, , D9, , D8, , D7, , D6, , D5, , D4, , D3, , A7, , A5, , A3, , 8, , 7, , 6, , 5, , 4, , 3, , 2, , 1, , 0 , - align=center !1 , ,
9-demicube (henne), , (1,1,1,1,1,1,1,1,1), , 274, , 2448, , 9888, , 23520, , 36288, , 37632, , 21404, , 4608, , 256, , 1.0606601 , - align=center !2 , ,
Truncated 9-demicube (thenne), , (1,1,3,3,3,3,3,3,3), , , , , , , , , , , , , , , , 69120 , , 9216, , 2.8504384 , - align=center !3 , ,
Cantellated 9-demicube, , (1,1,1,3,3,3,3,3,3), , , , , , , , , , , , , , , , 225792 , , 21504, , 2.6692696 , - align=center !4 , ,
Runcinated 9-demicube, , (1,1,1,1,3,3,3,3,3), , , , , , , , , , , , , , , , 419328 , , 32256, , 2.4748735 , - align=center !5 , ,
Stericated 9-demicube, , (1,1,1,1,1,3,3,3,3), , , , , , , , , , , , , , , , 483840 , , 32256, , 2.2638462 , - align=center !6 , ,
Pentellated 9-demicube, , (1,1,1,1,1,1,3,3,3), , , , , , , , , , , , , , , , 354816 , , 21504, , 2.0310094 , - align=center !7 , ,
Hexicated 9-demicube, , (1,1,1,1,1,1,1,3,3), , , , , , , , , , , , , , , , 161280 , , 9216, , 1.7677668 , - align=center !8 , ,
Heptellated 9-demicube, , (1,1,1,1,1,1,1,1,3), , , , , , , , , , , , , , , , 41472 , , 2304, , 1.4577379
Regular and uniform honeycombs
 There are five fundamental affine
There are five fundamental affine Coxeter groups
In mathematics, a Coxeter group, named after Harold Scott MacDonald Coxeter, H. S. M. Coxeter, is an group (mathematics), abstract group that admits a group presentation, formal description in terms of Reflection (mathematics), reflections (or Kal ...
that generate regular and uniform tessellations in 8-space:
{, class=wikitable
!#
!colspan=2, Coxeter group
In mathematics, a Coxeter group, named after H. S. M. Coxeter, is an abstract group that admits a formal description in terms of reflections (or kaleidoscopic mirrors). Indeed, the finite Coxeter groups are precisely the finite Euclidean refl ...
!Coxeter diagram
Harold Scott MacDonald "Donald" Coxeter, (9 February 1907 – 31 March 2003) was a British and later also Canadian geometer. He is regarded as one of the greatest geometers of the 20th century.
Biography
Coxeter was born in Kensington to ...
!Forms
, - align=center
, 1, , , , [9/sup>.html"_;"title=".html"_;"title="[9">[9/sup>">.html"_;"title="[9">[9/sup>.html" ;"title="">[9/sup>.html" ;"title=".html" ;"title=" [9/sup>">.html"_;"title="[9">[9/sup>">.html" ;"title="">[9/sup>">.html" ;"title="[9">[9/sup>">">, 45
, - align=center
, 2, , , , , , 271
, - align=center
, 3, , , , h , , 383 (128 new)
, - align=center
, 4, , , , q ,36,4br_/>[31,1,34,31,1.html" ;"title="1,1,34,31,1">,36,4br />[31,1,34,31,1">, , 155 (15 new)
, - align=center
, 5, , , , [35,2,1, , , 511
Regular and uniform tessellations include:
* 45 uniquely ringed forms
**8-simplex honeycomb: {3[9]}
* 271 uniquely ringed forms
** List of regular polytopes#Higher dimensions 3, Regular 8-cube honeycomb: {4,36,4},
* : 383 uniquely ringed forms, 255 shared with , 128 new
** 8-demicube honeycomb: h{4,36,4} or {31,1,35,4}, or
* , 1,1,34,31,1 155 unique ring permutations, and 15 are new, the first, , Coxeter called a quarter 8-cubic honeycomb, representing as q{4,36,4}, or qδ9.
* 511 forms
** 521 honeycomb:
** 251 honeycomb:
** 152 honeycomb:
Regular and uniform hyperbolic honeycombs
There are no compact hyperbolic Coxeter groups of rank 9, groups that can generate honeycombs with all finite facets, and a finitevertex figure
In geometry, a vertex figure, broadly speaking, is the figure exposed when a corner of a polyhedron or polytope is sliced off.
Definitions
Take some corner or Vertex (geometry), vertex of a polyhedron. Mark a point somewhere along each connect ...
. However, there are 4 paracompact hyperbolic Coxeter groups of rank 9, each generating uniform honeycombs in 8-space as permutations of rings of the Coxeter diagrams.
{, class=wikitable
, align= = ,3[8/sup>.html"_;"title=".html"_;"title=",3[8">,3[8/sup>">.html"_;"title=",3[8">,3[8/sup>.html" ;"title="">,3[8/sup>.html" ;"title=".html" ;"title=",3 ,3[8/sup>">.html"_;"title=",3[8">,3[8/sup>
">align=right.html" ;"title="">,3[8/sup>">.html" ;"title=",3[8">,3[8/sup>
">align=right"> = align= = align= = T._Gosset:_''On_the_Regular_and_Semi-Regular_Figures_in_Space_of_n_Dimensions'',_Messenger_of_Mathematics,_Macmillan,_1900 *_ T._Gosset:_''On_the_Regular_and_Semi-Regular_Figures_in_Space_of_n_Dimensions'',_Messenger_of_Mathematics,_Macmillan,_1900 *_Alicia_Boole_Stott">A._Boole_Stott:_''Geometrical_deduction_of_semiregular_from_regular_polytopes_and_space_fillings'',_Verhandelingen_of_the_Koninklijke_academy_van_Wetenschappen_width_unit_Amsterdam,_Eerste_Sectie_11,1,_Amsterdam,_1910 *_Harold_Scott_MacDonald_Coxeter.html" ;"title="Alicia_Boole_Stott.html" ;"title="Thorold Gosset">T. Gosset: ''On the Regular and Semi-Regular Figures in Space of n Dimensions'', Messenger of Mathematics, Macmillan, 1900 * Alicia Boole Stott">A. Boole Stott: ''Geometrical deduction of semiregular from regular polytopes and space fillings'', Verhandelingen of the Koninklijke academy van Wetenschappen width unit Amsterdam, Eerste Sectie 11,1, Amsterdam, 1910 * Harold Scott MacDonald Coxeter">H.S.M. Coxeter: ** H.S.M. Coxeter, M.S. Longuet-Higgins und J.C.P. Miller: ''Uniform Polyhedra'', Philosophical Transactions of the Royal Society of London, Londne, 1954 ** H.S.M. Coxeter, ''Regular Polytopes'', 3rd Edition, Dover New York, 1973 * Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995,
** (Paper 22) H.S.M. Coxeter, ''Regular and Semi Regular Polytopes I'', [Math. Zeit. 46 (1940) 380–407, MR 2,10] ** (Paper 23) H.S.M. Coxeter, ''Regular and Semi-Regular Polytopes II'', ath. Zeit. 188 (1985) 559-591** (Paper 24) H.S.M. Coxeter, ''Regular and Semi-Regular Polytopes III'', ath. Zeit. 200 (1988) 3-45* N.W. Johnson: ''The Theory of Uniform Polytopes and Honeycombs'', Ph.D. Dissertation, University of Toronto, 1966 *
External links
Polytope names
Jonathan Bowers
* {{Honeycombs 9-polytopes