|
Runcinated 9-simplex
In geometry, runcination is an operation that cuts a regular polytope (or honeycomb) simultaneously along the faces, edges, and vertices, creating new facets in place of the original face, edge, and vertex centers. It is a higher order truncation operation, following cantellation, and truncation. It is represented by an extended Schläfli symbol t0,3. This operation only exists for 4-polytopes or higher. This operation is dual-symmetric for regular uniform 4-polytopes and 3-space convex uniform honeycombs. For a regular 4-polytope, the original cells remain, but become separated. The gaps at the separated faces become p-gonal prisms. The gaps between the separated edges become r-gonal prisms. The gaps between the separated vertices become cells. The vertex figure for a regular 4-polytope is an ''q''-gonal antiprism (called an ''antipodium'' if ''p'' and ''r'' are different). For regular 4-polytopes/honeycombs, this operation is also called expansion by Alicia Bo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Runcinated Cubic Honeycomb
The cubic honeycomb or cubic cellulation is the only proper regular space-filling tessellation (or honeycomb) in Euclidean 3-space made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron. It is a self-dual tessellation with Schläfli symbol . John Horton Conway called this honeycomb a cubille. Related honeycombs It is part of a multidimensional family of hypercube honeycombs, with Schläfli symbols of the form , starting with the square tiling, in the plane. It is one of 28 uniform honeycombs using convex uniform polyhedral cells. Isometries of simple cubic lattices Simple cubic lattices can be distorted into lower symmetries, represented by lower crystal systems: Uniform colorings There is a large number of uniform colorings, derived from different symmetries. These include: Projections The ''cubic honeycomb'' can be orthogonally projected into the euclidean plane with various s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vertex Figure
In geometry, a vertex figure, broadly speaking, is the figure exposed when a corner of a polyhedron or polytope is sliced off. Definitions Take some corner or Vertex (geometry), vertex of a polyhedron. Mark a point somewhere along each connected edge. Draw lines across the connected faces, joining adjacent points around the face. When done, these lines form a complete circuit, i.e. a polygon, around the vertex. This polygon is the vertex figure. More precise formal definitions can vary quite widely, according to circumstance. For example Coxeter (e.g. 1948, 1954) varies his definition as convenient for the current area of discussion. Most of the following definitions of a vertex figure apply equally well to infinite tessellation, tilings or, by extension, to Honeycomb (geometry), space-filling tessellation with polytope Cell (geometry), cells and other higher-dimensional polytopes. As a flat slice Make a slice through the corner of the polyhedron, cutting through all the edges ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Runcinated 120-cell Verf
In geometry, runcination is an operation that cuts a regular polytope (or honeycomb) simultaneously along the faces, edges, and vertices, creating new facets in place of the original face, edge, and vertex centers. It is a higher order truncation operation, following cantellation, and truncation. It is represented by an extended Schläfli symbol t0,3. This operation only exists for 4-polytopes or higher. This operation is dual-symmetric for regular uniform 4-polytopes and 3-space convex uniform honeycombs. For a regular 4-polytope, the original cells remain, but become separated. The gaps at the separated faces become p-gonal prisms. The gaps between the separated edges become r-gonal prisms. The gaps between the separated vertices become cells. The vertex figure for a regular 4-polytope is an ''q''-gonal antiprism (called an ''antipodium'' if ''p'' and ''r'' are different). For regular 4-polytopes/honeycombs, this operation is also called expansion by Alicia Boole Stott ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Runcinated 120-cell
In four-dimensional geometry, a runcinated 120-cell (or ''runcinated 600-cell'') is a convex uniform 4-polytope, being a runcination (a 3rd order truncation) of the regular 120-cell. There are 4 degrees of runcinations of the 120-cell including with permutations truncations and cantellations. The ''runcinated 120-cell'' can be seen as an expansion applied to a regular 4-polytope, the 120-cell or 600-cell. Runcinated 120-cell The runcinated 120-cell or small disprismatohexacosihecatonicosachoron is a uniform 4-polytope. It has 2640 cells: 120 dodecahedra, 720 pentagonal prisms, 1200 triangular prisms, and 600 tetrahedra. Its vertex figure is a nonuniform triangular antiprism (equilateral-triangular antipodium): its bases represent a dodecahedron and a tetrahedron, and its flanks represent three triangular prisms and three pentagonal prisms. Alternate names * Runcinated 120-cell / Runcinated 600-cell (Norman W. Johnson) ** Runcinated hecatonicosachoron / Runcinated dodecacon ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Runcinated 24-cell Schlegel Halfsolid
In geometry, runcination is an operation that cuts a regular polytope (or honeycomb) simultaneously along the faces, edges, and vertices, creating new facets in place of the original face, edge, and vertex centers. It is a higher order truncation operation, following cantellation, and truncation. It is represented by an extended Schläfli symbol t0,3. This operation only exists for 4-polytopes or higher. This operation is dual-symmetric for regular uniform 4-polytopes and 3-space convex uniform honeycombs. For a regular 4-polytope, the original cells remain, but become separated. The gaps at the separated faces become p-gonal prisms. The gaps between the separated edges become r-gonal prisms. The gaps between the separated vertices become cells. The vertex figure for a regular 4-polytope is an ''q''-gonal antiprism (called an ''antipodium'' if ''p'' and ''r'' are different). For regular 4-polytopes/honeycombs, this operation is also called expansion by Alicia Boole Stott ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Runcinated 24-cell Verf
In geometry, runcination is an operation that cuts a regular polytope (or honeycomb) simultaneously along the faces, edges, and vertices, creating new facets in place of the original face, edge, and vertex centers. It is a higher order truncation operation, following cantellation, and truncation. It is represented by an extended Schläfli symbol t0,3. This operation only exists for 4-polytopes or higher. This operation is dual-symmetric for regular uniform 4-polytopes and 3-space convex uniform honeycombs. For a regular 4-polytope, the original cells remain, but become separated. The gaps at the separated faces become p-gonal prisms. The gaps between the separated edges become r-gonal prisms. The gaps between the separated vertices become cells. The vertex figure for a regular 4-polytope is an ''q''-gonal antiprism (called an ''antipodium'' if ''p'' and ''r'' are different). For regular 4-polytopes/honeycombs, this operation is also called expansion by Alicia Boole Stott ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Runcinated 24-cell
In four-dimensional geometry, a runcinated 24-cell is a convex uniform 4-polytope, being a runcination (a 3rd order truncation) of the regular 24-cell. There are 3 unique degrees of runcinations of the 24-cell including with permutations truncations and cantellations. Runcinated 24-cell In geometry, the runcinated 24-cell or small prismatotetracontoctachoron is a uniform 4-polytope bounded by 48 octahedra and 192 triangular prisms. The octahedral cells correspond with the cells of a 24-cell and its dual. E. L. Elte identified it in 1912 as a semiregular polytope. Alternate names * Runcinated 24-cell ( Norman W. Johnson) * Runcinated icositetrachoron * Runcinated polyoctahedron * Small prismatotetracontoctachoron (spic) (Jonathan Bowers) Coordinates The Cartesian coordinates of the runcinated 24-cell having edge length 2 is given by all permutations of sign and coordinates of: : (0, 0, , 2+) : (1, 1, 1+, 1+) The permutations of the second set of coordinates coinc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
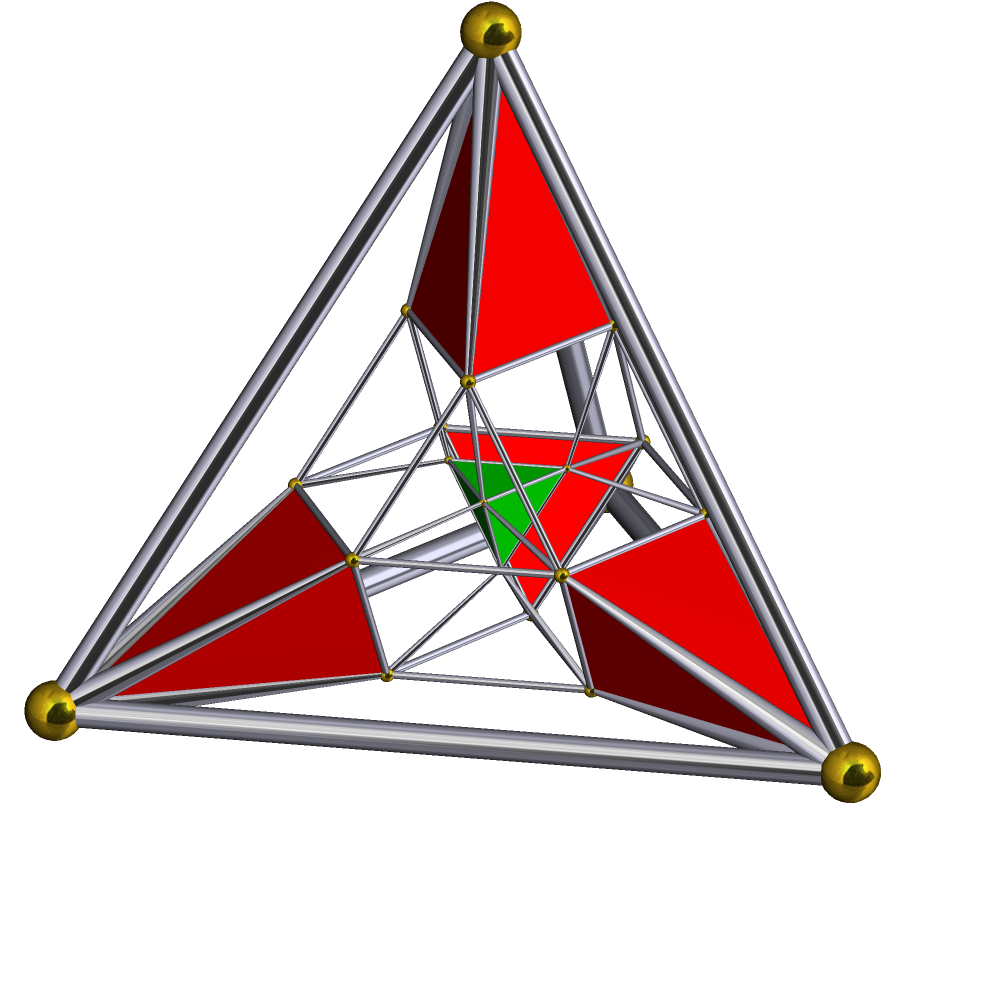
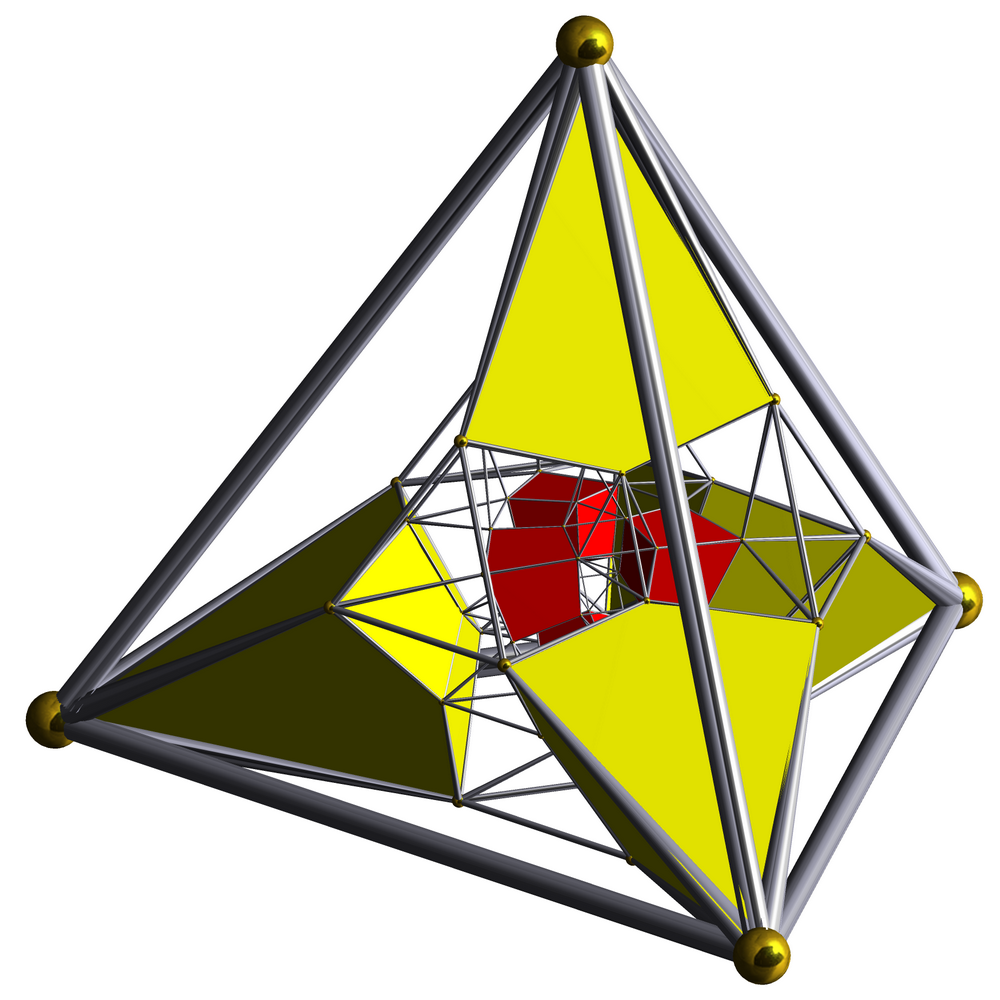
Schlegel Half-solid Runcinated 8-cell
Schlegel is a German occupational surname. Notable people with the surname include: * Anthony Schlegel (born 1981), former American football linebacker * August Wilhelm Schlegel (1767–1845), German poet, older brother of Friedrich * Brad Schlegel (born 1968), Canadian ice hockey player * Bernhard Schlegel (born 1951), German-Canadian chemist and professor at Wayne State University * Carmela Schlegel (born 1983), retired Swiss swimmer * Catharina von Schlegel (1697 – after 1768), German hymn writer * Dorothea von Schlegel (1764–1839), German novelist and translator, wife of Friedrich Schlegel * Elfi Schlegel (born 1964), former Canadian gymnast and sportscaster for NBC Sports * Frits Schlegel (1896–1965), Danish architect * Gustaaf Schlegel (1840–1903), Dutch sinologist and field naturalist * Hans Schlegel (born 1951), German astronaut * Helmut Schlegel (born 1943), German Franciscan, priest, author, meditation instructor, songwriter * Hermann Schlegel (1804–1884), German ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Schlegel Half-solid Runcinated 16-cell
Schlegel is a German occupational surname. Notable people with the surname include: * Anthony Schlegel (born 1981), former American football linebacker * August Wilhelm Schlegel (1767–1845), German poet, older brother of Friedrich * Brad Schlegel (born 1968), Canadian ice hockey player * Bernhard Schlegel (born 1951), German-Canadian chemist and professor at Wayne State University * Carmela Schlegel (born 1983), retired Swiss swimmer * Catharina von Schlegel (1697 – after 1768), German hymn writer * Dorothea von Schlegel (1764–1839), German novelist and translator, wife of Friedrich Schlegel * Elfi Schlegel (born 1964), former Canadian gymnast and sportscaster for NBC Sports * Frits Schlegel (1896–1965), Danish architect * Gustaaf Schlegel (1840–1903), Dutch sinologist and field naturalist * Hans Schlegel (born 1951), German astronaut * Helmut Schlegel (born 1943), German Franciscan, priest, author, meditation instructor, songwriter * Hermann Schlegel (1804–1884), German ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Runcinated 8-cell Verf
In geometry, runcination is an operation that cuts a regular polytope (or honeycomb) simultaneously along the faces, edges, and vertices, creating new facets in place of the original face, edge, and vertex centers. It is a higher order truncation operation, following cantellation, and truncation. It is represented by an extended Schläfli symbol t0,3. This operation only exists for 4-polytopes or higher. This operation is dual-symmetric for regular uniform 4-polytopes and 3-space convex uniform honeycombs. For a regular 4-polytope, the original cells remain, but become separated. The gaps at the separated faces become p-gonal prisms. The gaps between the separated edges become r-gonal prisms. The gaps between the separated vertices become cells. The vertex figure for a regular 4-polytope is an ''q''-gonal antiprism (called an ''antipodium'' if ''p'' and ''r'' are different). For regular 4-polytopes/honeycombs, this operation is also called expansion by Alicia Boole Stott ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Runcinated 16-cell
In four-dimensional geometry, a runcinated tesseract (or ''runcinated 16-cell'') is a convex uniform 4-polytope, being a runcination (a 3rd order truncation) of the regular tesseract. There are 4 variations of runcinations of the tesseract including with permutations truncations and cantellations. Runcinated tesseract The runcinated tesseract or (small) disprismatotesseractihexadecachoron has 16 tetrahedra, 32 cubes, and 32 triangular prisms. Each vertex is shared by 4 cubes, 3 triangular prisms and one tetrahedron. Construction The runcinated tesseract may be constructed by expanding the cells of a tesseract radially, and filling in the gaps with tetrahedra (vertex figures), cubes (face prisms), and triangular prisms (edge figure prisms). The same process applied to a 16-cell also yields the same figure. Cartesian coordinates The Cartesian coordinates of the vertices of the runcinated tesseract with edge length 2 are all permutations of: :\left(\pm 1,\ \pm 1,\ \pm 1,\ \p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
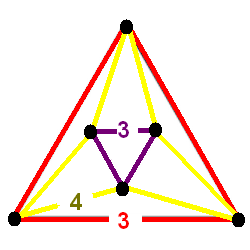
Schlegel Half-solid Runcinated 5-cell
Schlegel is a German occupational surname. Notable people with the surname include: * Anthony Schlegel (born 1981), former American football linebacker * August Wilhelm Schlegel (1767–1845), German poet, older brother of Friedrich * Brad Schlegel (born 1968), Canadian ice hockey player * Bernhard Schlegel (born 1951), German-Canadian chemist and professor at Wayne State University * Carmela Schlegel (born 1983), retired Swiss swimmer * Catharina von Schlegel (1697 – after 1768), German hymn writer * Dorothea von Schlegel (1764–1839), German novelist and translator, wife of Friedrich Schlegel * Elfi Schlegel (born 1964), former Canadian gymnast and sportscaster for NBC Sports * Frits Schlegel (1896–1965), Danish architect * Gustaaf Schlegel (1840–1903), Dutch sinologist and field naturalist * Hans Schlegel (born 1951), German astronaut * Helmut Schlegel (born 1943), German Franciscan, priest, author, meditation instructor, songwriter * Hermann Schlegel (1804–1884), German ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |