Trapeziform on:
[Wikipedia]
[Google]
[Amazon]
A quadrilateral with at least one pair of parallel sides is called a trapezoid () in American and Canadian English. In British and other forms of English, it is called a trapezium ().
A trapezoid is necessarily a convex quadrilateral in Euclidean geometry. The parallel sides are called the ''bases'' of the trapezoid. The other two sides are called the ''legs'' (or the ''lateral sides'') if they are not parallel; otherwise, the trapezoid is a parallelogram, and there are two pairs of bases). A ''scalene trapezoid'' is a trapezoid with no sides of equal measure, in contrast with the
 Ancient Greek mathematician Euclid defined five types of quadrilateral, of which four had two sets of parallel sides (known in English as square, rectangle, rhombus and rhomboid) and the last did not have two sets of parallel sides – a τραπέζια (''trapezia'' literally "a table", itself from τετράς (''tetrás''), "four" + πέζα (''péza''), "a foot; end, border, edge").
Two types of ''trapezia'' were introduced by
Ancient Greek mathematician Euclid defined five types of quadrilateral, of which four had two sets of parallel sides (known in English as square, rectangle, rhombus and rhomboid) and the last did not have two sets of parallel sides – a τραπέζια (''trapezia'' literally "a table", itself from τετράς (''tetrás''), "four" + πέζα (''péza''), "a foot; end, border, edge").
Two types of ''trapezia'' were introduced by
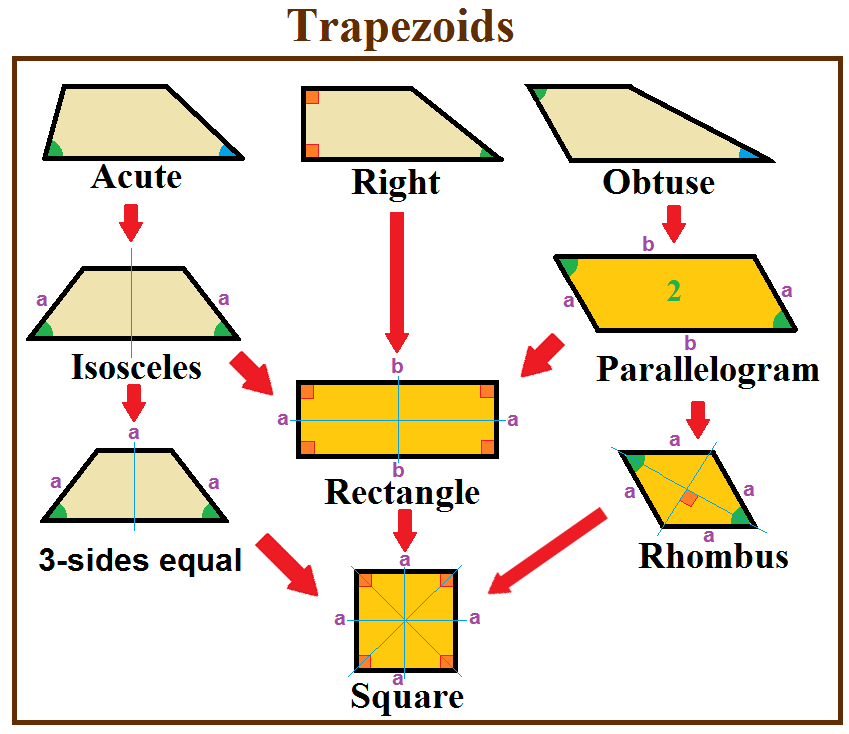 A right trapezoid (also called ''right-angled trapezoid'') has two adjacent right angles. Right trapezoids are used in the trapezoidal rule for estimating areas under a curve.
An acute trapezoid has two adjacent acute angles on its longer ''base'' edge, while an obtuse trapezoid has one acute and one obtuse angle on each ''base''.
An isosceles trapezoid is a trapezoid where the base angles have the same measure. As a consequence the two legs are also of equal length and it has reflection symmetry. This is possible for acute trapezoids or right trapezoids (rectangles).
A
A right trapezoid (also called ''right-angled trapezoid'') has two adjacent right angles. Right trapezoids are used in the trapezoidal rule for estimating areas under a curve.
An acute trapezoid has two adjacent acute angles on its longer ''base'' edge, while an obtuse trapezoid has one acute and one obtuse angle on each ''base''.
An isosceles trapezoid is a trapezoid where the base angles have the same measure. As a consequence the two legs are also of equal length and it has reflection symmetry. This is possible for acute trapezoids or right trapezoids (rectangles).
A
 Given a convex quadrilateral, the following properties are equivalent, and each implies that the quadrilateral is a trapezoid:
*It has two adjacent angles that are
Given a convex quadrilateral, the following properties are equivalent, and each implies that the quadrilateral is a trapezoid:
*It has two adjacent angles that are
"Characterizations of trapezoids"
Forum Geometricorum, 13 (2013) 23-35. *The product of the areas of the two triangles formed by one diagonal equals the product of the areas of the two triangles formed by the other diagonal. *The areas ''S'' and ''T'' of some two opposite triangles of the four triangles formed by the diagonals satisfy the equation :: :where ''K'' is the area of the quadrilateral. *The midpoints of two opposite sides and the intersection of the diagonals are collinear. *The angles in the quadrilateral ''ABCD'' satisfy *The cosines of two adjacent angles sum to 0, as do the cosines of the other two angles. *The cotangents of two adjacent angles sum to 0, as do the cotangents of the other two adjacent angles. *One bimedian divides the quadrilateral into two quadrilaterals of equal areas. *Twice the length of the bimedian connecting the midpoints of two opposite sides equals the sum of the lengths of the other sides. Additionally, the following properties are equivalent, and each implies that opposite sides ''a'' and ''b'' are parallel: * The consecutive sides ''a'', ''c'', ''b'', ''d'' and the diagonals ''p'', ''q'' satisfy the equation :: *The distance ''v'' between the midpoints of the diagonals satisfies the equation ::
 The lengths of the diagonals are
:
:
where ''a'' is the short base, ''b'' is the long base, and ''c'' and ''d'' are the trapezoid legs.
If the trapezoid is divided into four triangles by its diagonals ''AC'' and ''BD'' (as shown on the right), intersecting at ''O'', then the area of is equal to that of , and the product of the areas of and is equal to that of and . The ratio of the areas of each pair of adjacent triangles is the same as that between the lengths of the parallel sides.
Let the trapezoid have vertices ''A'', ''B'', ''C'', and ''D'' in sequence and have parallel sides ''AB'' and ''DC''. Let ''E'' be the intersection of the diagonals, and let ''F'' be on side ''DA'' and ''G'' be on side ''BC'' such that ''FEG'' is parallel to ''AB'' and ''CD''. Then ''FG'' is the
The lengths of the diagonals are
:
:
where ''a'' is the short base, ''b'' is the long base, and ''c'' and ''d'' are the trapezoid legs.
If the trapezoid is divided into four triangles by its diagonals ''AC'' and ''BD'' (as shown on the right), intersecting at ''O'', then the area of is equal to that of , and the product of the areas of and is equal to that of and . The ratio of the areas of each pair of adjacent triangles is the same as that between the lengths of the parallel sides.
Let the trapezoid have vertices ''A'', ''B'', ''C'', and ''D'' in sequence and have parallel sides ''AB'' and ''DC''. Let ''E'' be the intersection of the diagonals, and let ''F'' be on side ''DA'' and ''G'' be on side ''BC'' such that ''FEG'' is parallel to ''AB'' and ''CD''. Then ''FG'' is the
Methods for Euclidean Geometry
', Mathematical Association of America, 2010, p. 55. :
 In morphology, Taxonomy (biology), taxonomy and other descriptive disciplines in which a term for such shapes is necessary, terms such as ''trapezoidal'' or ''trapeziform'' commonly are useful in descriptions of particular organs or forms.
In morphology, Taxonomy (biology), taxonomy and other descriptive disciplines in which a term for such shapes is necessary, terms such as ''trapezoidal'' or ''trapeziform'' commonly are useful in descriptions of particular organs or forms.
''Common properties of trapezoids and convex quadrilaterals''
"Trapezium"
at ''Encyclopedia of Mathematics'' *
Trapezoid definition
With interactive animations
Trapezoid (North America)
at elsy.at: Animated course (construction, circumference, area)
on ''Numerical Methods for Stem Undergraduate'' * Autar Kaw and E. Eric Kalu,
', (2008) {{Polygons Elementary shapes Types of quadrilaterals
special cases
Special or specials may refer to:
Policing
* Specials, Ulster Special Constabulary, the Northern Ireland police force
* Specials, Special Constable, an auxiliary, volunteer, or temporary; police worker or police officer
Literature
* ''Specia ...
below.
Etymology and ''trapezium'' versus ''trapezoid''
 Ancient Greek mathematician Euclid defined five types of quadrilateral, of which four had two sets of parallel sides (known in English as square, rectangle, rhombus and rhomboid) and the last did not have two sets of parallel sides – a τραπέζια (''trapezia'' literally "a table", itself from τετράς (''tetrás''), "four" + πέζα (''péza''), "a foot; end, border, edge").
Two types of ''trapezia'' were introduced by
Ancient Greek mathematician Euclid defined five types of quadrilateral, of which four had two sets of parallel sides (known in English as square, rectangle, rhombus and rhomboid) and the last did not have two sets of parallel sides – a τραπέζια (''trapezia'' literally "a table", itself from τετράς (''tetrás''), "four" + πέζα (''péza''), "a foot; end, border, edge").
Two types of ''trapezia'' were introduced by Proclus
Proclus Lycius (; 8 February 412 – 17 April 485), called Proclus the Successor ( grc-gre, Πρόκλος ὁ Διάδοχος, ''Próklos ho Diádokhos''), was a Greek Neoplatonist philosopher, one of the last major classical philosophers ...
(412 to 485 AD) in his commentary on the first book of Euclid's Elements:
* one pair of parallel sides – a ''trapezium'' (τραπέζιον), divided into isosceles (equal legs) and scalene (unequal) trapezia
* no parallel sides – ''trapezoid'' (τραπεζοειδή, ''trapezoeidé'', literally trapezium-like ( εἶδος means "resembles"), in the same way as cuboid
In geometry, a cuboid is a hexahedron, a six-faced solid. Its faces are quadrilaterals. Cuboid means "like a cube", in the sense that by adjusting the length of the edges or the angles between edges and faces a cuboid can be transformed into a cub ...
means cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. Viewed from a corner it is a hexagon and its net is usually depicted as a cross.
The cube is the only r ...
-like and rhomboid means rhombus-like)
All European languages follow Proclus's structure as did English until the late 18th century, until an influential mathematical dictionary published by Charles Hutton in 1795 supported without explanation a transposition of the terms. This mistake was corrected in British English in about 1875, but was retained in American English into the modern day.
The following is a table comparing usages, with the most specific definitions at the top to the most general at the bottom.
Inclusive vs exclusive definition
There is some disagreement whetherparallelogram
In Euclidean geometry, a parallelogram is a simple (non- self-intersecting) quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equa ...
s, which have two pairs of parallel sides, should be regarded as trapezoids. Some define a trapezoid as a quadrilateral having ''only'' one pair of parallel sides (the exclusive definition), thereby excluding parallelograms. Others define a trapezoid as a quadrilateral with ''at least'' one pair of parallel sides (the inclusive definition), making the parallelogram a special type of trapezoid. The latter definition is consistent with its uses in higher mathematics such as calculus. This article uses the inclusive definition and considers parallelograms as special cases of a trapezoid. This is also advocated in the taxonomy of quadrilaterals.
Under the inclusive definition, all parallelograms (including rhombuses, squares and non-square rectangle
In Euclidean plane geometry, a rectangle is a quadrilateral with four right angles. It can also be defined as: an equiangular quadrilateral, since equiangular means that all of its angles are equal (360°/4 = 90°); or a parallelogram containi ...
s) are trapezoids. Rectangles have mirror symmetry on mid-edges; rhombuses have mirror symmetry on vertices, while squares have mirror symmetry on both mid-edges and vertices.
Special cases
 A right trapezoid (also called ''right-angled trapezoid'') has two adjacent right angles. Right trapezoids are used in the trapezoidal rule for estimating areas under a curve.
An acute trapezoid has two adjacent acute angles on its longer ''base'' edge, while an obtuse trapezoid has one acute and one obtuse angle on each ''base''.
An isosceles trapezoid is a trapezoid where the base angles have the same measure. As a consequence the two legs are also of equal length and it has reflection symmetry. This is possible for acute trapezoids or right trapezoids (rectangles).
A
A right trapezoid (also called ''right-angled trapezoid'') has two adjacent right angles. Right trapezoids are used in the trapezoidal rule for estimating areas under a curve.
An acute trapezoid has two adjacent acute angles on its longer ''base'' edge, while an obtuse trapezoid has one acute and one obtuse angle on each ''base''.
An isosceles trapezoid is a trapezoid where the base angles have the same measure. As a consequence the two legs are also of equal length and it has reflection symmetry. This is possible for acute trapezoids or right trapezoids (rectangles).
A parallelogram
In Euclidean geometry, a parallelogram is a simple (non- self-intersecting) quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equa ...
is a trapezoid with two pairs of parallel sides. A parallelogram has central 2-fold rotational symmetry (or point reflection symmetry). It is possible for obtuse trapezoids or right trapezoids (rectangles).
A tangential trapezoid is a trapezoid that has an incircle.
A Saccheri quadrilateral
A Saccheri quadrilateral (also known as a Khayyam–Saccheri quadrilateral) is a quadrilateral with two equal sides perpendicular to the base. It is named after Giovanni Gerolamo Saccheri, who used it extensively in his book ''Euclides ab omni na ...
is similar to a trapezoid in the hyperbolic plane, with two adjacent right angles, while it is a rectangle in the Euclidean plane. A Lambert quadrilateral in the hyperbolic plane has 3 right angles.
Condition of existence
Four lengths ''a'', ''c'', ''b'', ''d'' can constitute the consecutive sides of a non-parallelogram trapezoid with ''a'' and ''b'' parallel only when : The quadrilateral is a parallelogram when , but it is an ex-tangential quadrilateral (which is not a trapezoid) when .Characterizations
supplementary
The term supplementary can refer to:
* Supplementary angles
* Supplementary Benefit, a former benefit payable in the United Kingdom
* Supplementary question, a type of question asked during a questioning time for prime minister
See also
* Sup ...
, that is, they add up to 180 degrees.
*The angle between a side and a diagonal is equal to the angle between the opposite side and the same diagonal.
*The diagonals cut each other in mutually the same ratio (this ratio is the same as that between the lengths of the parallel sides).
*The diagonals cut the quadrilateral into four triangles of which one opposite pair have equal areas.Martin Josefsson"Characterizations of trapezoids"
Forum Geometricorum, 13 (2013) 23-35. *The product of the areas of the two triangles formed by one diagonal equals the product of the areas of the two triangles formed by the other diagonal. *The areas ''S'' and ''T'' of some two opposite triangles of the four triangles formed by the diagonals satisfy the equation :: :where ''K'' is the area of the quadrilateral. *The midpoints of two opposite sides and the intersection of the diagonals are collinear. *The angles in the quadrilateral ''ABCD'' satisfy *The cosines of two adjacent angles sum to 0, as do the cosines of the other two angles. *The cotangents of two adjacent angles sum to 0, as do the cotangents of the other two adjacent angles. *One bimedian divides the quadrilateral into two quadrilaterals of equal areas. *Twice the length of the bimedian connecting the midpoints of two opposite sides equals the sum of the lengths of the other sides. Additionally, the following properties are equivalent, and each implies that opposite sides ''a'' and ''b'' are parallel: * The consecutive sides ''a'', ''c'', ''b'', ''d'' and the diagonals ''p'', ''q'' satisfy the equation :: *The distance ''v'' between the midpoints of the diagonals satisfies the equation ::
Midsegment and height
The ''midsegment'' (also called the median or midline) of a trapezoid is the segment that joins the midpoints of the legs. It is parallel to the bases. Its length ''m'' is equal to the average of the lengths of the bases ''a'' and ''b'' of the trapezoid, : The midsegment of a trapezoid is one of the two bimedians (the other bimedian divides the trapezoid into equal areas). The ''height'' (or altitude) is the perpendicular distance between the bases. In the case that the two bases have different lengths (''a'' ≠ ''b''), the height of a trapezoid ''h'' can be determined by the length of its four sides using the formula : where ''c'' and ''d'' are the lengths of the legs.Area
The area ''K'' of a trapezoid is given by : where ''a'' and ''b'' are the lengths of the parallel sides, ''h'' is the height (the perpendicular distance between these sides), and ''m'' is thearithmetic mean
In mathematics and statistics, the arithmetic mean ( ) or arithmetic average, or just the ''mean'' or the ''average'' (when the context is clear), is the sum of a collection of numbers divided by the count of numbers in the collection. The colle ...
of the lengths of the two parallel sides. In 499 AD Aryabhata, a great mathematician- astronomer from the classical age of Indian mathematics
Indian mathematics emerged in the Indian subcontinent from 1200 BCE until the end of the 18th century. In the classical period of Indian mathematics (400 CE to 1200 CE), important contributions were made by scholars like Aryabhata, Brahmagupta ...
and Indian astronomy, used this method in the ''Aryabhatiya
''Aryabhatiya'' (IAST: ') or ''Aryabhatiyam'' ('), a Sanskrit astronomical treatise, is the ''magnum opus'' and only known surviving work of the 5th century Indian mathematician Aryabhata. Philosopher of astronomy Roger Billard estimates that th ...
'' (section 2.8). This yields as a special case the well-known formula for the area of a triangle, by considering a triangle as a degenerate trapezoid in which one of the parallel sides has shrunk to a point.
The 7th-century Indian mathematician Bhāskara I derived the following formula for the area of a trapezoid with consecutive sides ''a'', ''c'', ''b'', ''d'':
:
where ''a'' and ''b'' are parallel and ''b'' > ''a''. This formula can be factored into a more symmetric version
:
When one of the parallel sides has shrunk to a point (say ''a'' = 0), this formula reduces to Heron's formula for the area of a triangle.
Another equivalent formula for the area, which more closely resembles Heron's formula, is
:
:
where is the semiperimeter of the trapezoid. (This formula is similar to Brahmagupta's formula, but it differs from it, in that a trapezoid might not be cyclic (inscribed in a circle). The formula is also a special case of Bretschneider's formula for a general quadrilateral).
From Bretschneider's formula, it follows that
:
The line that joins the midpoints of the parallel sides, bisects the area.
Diagonals
harmonic mean
In mathematics, the harmonic mean is one of several kinds of average, and in particular, one of the Pythagorean means. It is sometimes appropriate for situations when the average rate is desired.
The harmonic mean can be expressed as the recipro ...
of ''AB'' and ''DC'':
:
The line that goes through both the intersection point of the extended nonparallel sides and the intersection point of the diagonals, bisects each base.
Other properties
The center of area (center of mass for a uniform lamina) lies along the line segment joining the midpoints of the parallel sides, at a perpendicular distance ''x'' from the longer side ''b'' given by : The center of area divides this segment in the ratio (when taken from the short to the long side) : If the angle bisectors to angles ''A'' and ''B'' intersect at ''P'', and the angle bisectors to angles ''C'' and ''D'' intersect at ''Q'', thenOwen Byer, Felix Lazebnik andDeirdre Smeltzer
Deirdre Longacher Smeltzer (born 1964) is an American mathematician, mathematics educator, textbook author, and academic administrator. A former professor, dean, and vice president at Eastern Mennonite University, she is Senior Director for Pro ...
, Methods for Euclidean Geometry
', Mathematical Association of America, 2010, p. 55. :
Applications
Architecture
In architecture the word is used to refer to symmetrical doors, windows, and buildings built wider at the base, tapering toward the top, in Egyptian style. If these have straight sides and sharp angular corners, their shapes are usually isosceles trapezoids. This was the standard style for the doors and windows of the Inca.Geometry
Thecrossed ladders problem The crossed ladders problem is a puzzle of unknown origin that has appeared in various publications and regularly reappears in Web pages and Usenet discussions.
The problem
Two ladders of lengths ''a'' and ''b'' lie oppositely across an alley, a ...
is the problem of finding the distance between the parallel sides of a right trapezoid, given the diagonal lengths and the distance from the perpendicular leg to the diagonal intersection.
Biology
 In morphology, Taxonomy (biology), taxonomy and other descriptive disciplines in which a term for such shapes is necessary, terms such as ''trapezoidal'' or ''trapeziform'' commonly are useful in descriptions of particular organs or forms.
In morphology, Taxonomy (biology), taxonomy and other descriptive disciplines in which a term for such shapes is necessary, terms such as ''trapezoidal'' or ''trapeziform'' commonly are useful in descriptions of particular organs or forms.
Computer engineering
In computer engineering, specifically digital logic and computer architecture, trapezoids are typically utilized to symbolize Multiplexer, multiplexors. Multiplexors are logic elements that select between multiple elements and produce a single output based on a select signal. Typical designs will employ trapezoids without specifically stating they are multiplexors as they are universally equivalent.See also
* Frustum, a solid having trapezoidal faces * Polite number, also known as a trapezoidal number * Wedge (geometry), Wedge, a polyhedron defined by two triangles and three trapezoid faces.References
Further reading
*D. Fraivert, A. Sigler and M. Stupel''Common properties of trapezoids and convex quadrilaterals''
External links
"Trapezium"
at ''Encyclopedia of Mathematics'' *
Trapezoid definition
With interactive animations
Trapezoid (North America)
at elsy.at: Animated course (construction, circumference, area)
on ''Numerical Methods for Stem Undergraduate'' * Autar Kaw and E. Eric Kalu,
', (2008) {{Polygons Elementary shapes Types of quadrilaterals