Stationary wave on:
[Wikipedia]
[Google]
[Amazon]
 In
In
 This boundary condition is in the form of the Sturm–Liouville formulation. The latter boundary condition is satisfied when . ''L'' is given, so the boundary condition restricts the wavelength of the standing waves to
:
Waves can only form standing waves on this string if they have a wavelength that satisfies this relationship with ''L''. If waves travel with speed ''v'' along the string, then equivalently the frequency of the standing waves is restricted to
:
The standing wave with oscillates at the
This boundary condition is in the form of the Sturm–Liouville formulation. The latter boundary condition is satisfied when . ''L'' is given, so the boundary condition restricts the wavelength of the standing waves to
:
Waves can only form standing waves on this string if they have a wavelength that satisfies this relationship with ''L''. If waves travel with speed ''v'' along the string, then equivalently the frequency of the standing waves is restricted to
:
The standing wave with oscillates at the
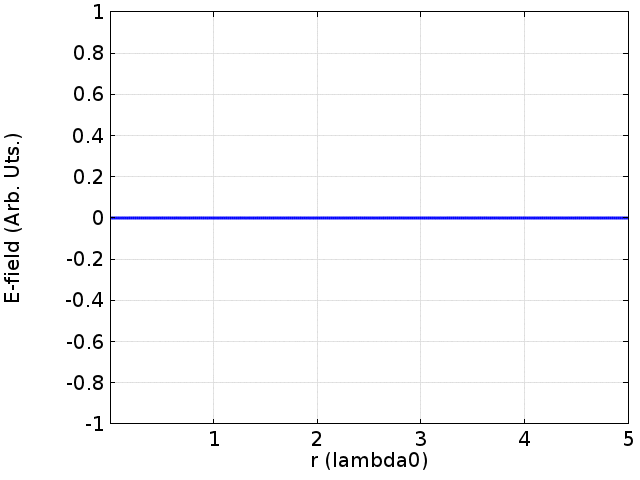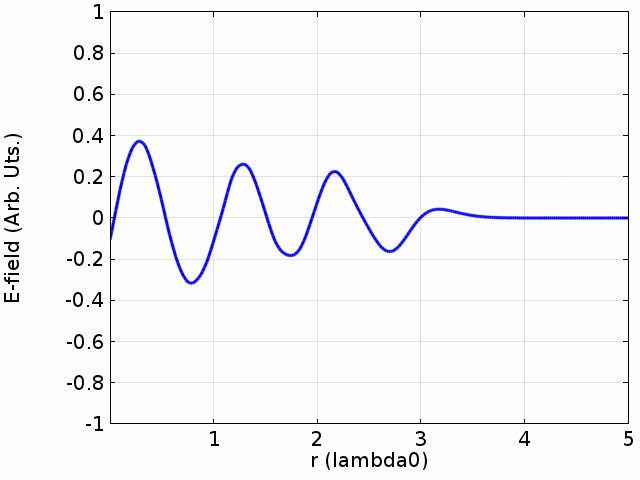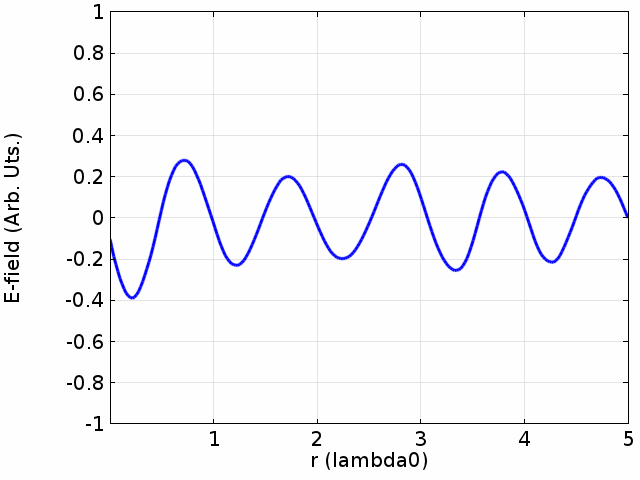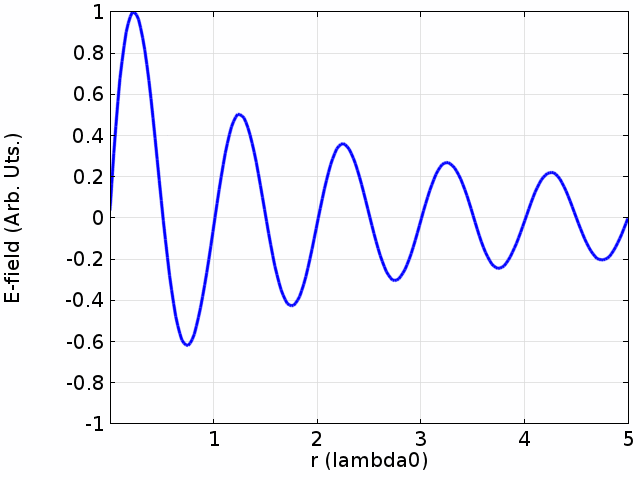 Next, consider the same string of length ''L'', but this time it is only fixed at . At , the string is free to move in the ''y'' direction. For example, the string might be tied at to a ring that can slide freely up and down a pole. The string again has small damping and is driven by a small driving force at .
In this case, Equation () still describes the standing wave pattern that can form on the string, and the string has the same boundary condition of at . However, at where the string can move freely there should be an anti-node with maximal amplitude of ''y''. Equivalently, this boundary condition of the "free end" can be stated as at , which is in the form of the Sturm–Liouville formulation. The intuition for this boundary condition at is that the motion of the "free end" will follow that of the point to its left.
Reviewing Equation (), for the largest amplitude of ''y'' occurs when , or
:
This leads to a different set of wavelengths than in the two-fixed-ends example. Here, the wavelength of the standing waves is restricted to
:
:
Equivalently, the frequency is restricted to
:
Note that in this example ''n'' only takes odd values. Because ''L'' is an anti-node, it is an ''odd'' multiple of a quarter wavelength. Thus the fundamental mode in this example only has one quarter of a complete sine cycle–zero at and the first peak at –the first harmonic has three quarters of a complete sine cycle, and so on.
This example also demonstrates a type of resonance and the frequencies that produce standing waves are called ''resonant frequencies''.
Next, consider the same string of length ''L'', but this time it is only fixed at . At , the string is free to move in the ''y'' direction. For example, the string might be tied at to a ring that can slide freely up and down a pole. The string again has small damping and is driven by a small driving force at .
In this case, Equation () still describes the standing wave pattern that can form on the string, and the string has the same boundary condition of at . However, at where the string can move freely there should be an anti-node with maximal amplitude of ''y''. Equivalently, this boundary condition of the "free end" can be stated as at , which is in the form of the Sturm–Liouville formulation. The intuition for this boundary condition at is that the motion of the "free end" will follow that of the point to its left.
Reviewing Equation (), for the largest amplitude of ''y'' occurs when , or
:
This leads to a different set of wavelengths than in the two-fixed-ends example. Here, the wavelength of the standing waves is restricted to
:
:
Equivalently, the frequency is restricted to
:
Note that in this example ''n'' only takes odd values. Because ''L'' is an anti-node, it is an ''odd'' multiple of a quarter wavelength. Thus the fundamental mode in this example only has one quarter of a complete sine cycle–zero at and the first peak at –the first harmonic has three quarters of a complete sine cycle, and so on.
This example also demonstrates a type of resonance and the frequencies that produce standing waves are called ''resonant frequencies''.
 So far, the wave has been written in terms of its pressure as a function of position ''x'' and time. Alternatively, the wave can be written in terms of its longitudinal displacement of air, where air in a segment of the pipe moves back and forth slightly in the ''x''-direction as the pressure varies and waves travel in either or both directions. The change in pressure Δ''p'' and longitudinal displacement ''s'' are related as
:
where ''ρ'' is the
So far, the wave has been written in terms of its pressure as a function of position ''x'' and time. Alternatively, the wave can be written in terms of its longitudinal displacement of air, where air in a segment of the pipe moves back and forth slightly in the ''x''-direction as the pressure varies and waves travel in either or both directions. The change in pressure Δ''p'' and longitudinal displacement ''s'' are related as
:
where ''ρ'' is the
 In
In physics
Physics is the natural science that studies matter, its fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which r ...
, a standing wave, also known as a stationary wave, is a wave
In physics, mathematics, and related fields, a wave is a propagating dynamic disturbance (change from equilibrium) of one or more quantities. Waves can be periodic, in which case those quantities oscillate repeatedly about an equilibrium (res ...
that oscillates in time but whose peak amplitude profile does not move in space. The peak amplitude
The amplitude of a periodic variable is a measure of its change in a single period (such as time or spatial period). The amplitude of a non-periodic signal is its magnitude compared with a reference value. There are various definitions of amplit ...
of the wave oscillations at any point in space is constant with respect to time, and the oscillations at different points throughout the wave are in phase
In physics and mathematics, the phase of a periodic function F of some real variable t (such as time) is an angle-like quantity representing the fraction of the cycle covered up to t. It is denoted \phi(t) and expressed in such a scale that it v ...
. The locations at which the absolute value of the amplitude is minimum are called nodes
In general, a node is a localized swelling (a "knot") or a point of intersection (a Vertex (graph theory), vertex).
Node may refer to:
In mathematics
*Vertex (graph theory), a vertex in a mathematical graph
*Vertex (geometry), a point where two ...
, and the locations where the absolute value of the amplitude is maximum are called antinode
A node is a point along a standing wave where the wave has minimum amplitude. For instance, in a vibrating guitar string, the ends of the string are nodes. By changing the position of the end node through frets, the guitarist changes the effect ...
s.
Standing waves were first noticed by Michael Faraday
Michael Faraday (; 22 September 1791 – 25 August 1867) was an English scientist who contributed to the study of electromagnetism and electrochemistry. His main discoveries include the principles underlying electromagnetic inducti ...
in 1831. Faraday observed standing waves on the surface of a liquid in a vibrating container. Franz Melde
Franz Emil Melde (March 11, 1832 in Großenlüder near Fulda – March 17, 1901 in Marburg) was a German physicist and professor. A graduate of the University of Marburg under Christian Ludwig Gerling, he later taught there, focusing primar ...
coined the term "standing wave" (German: ''stehende Welle'' or ''Stehwelle'') around 1860 and demonstrated the phenomenon in his classic experiment with vibrating strings.
This phenomenon can occur because the medium is moving in the direction opposite to the movement of the wave, or it can arise in a stationary medium as a result of interference
Interference is the act of interfering, invading, or poaching. Interference may also refer to:
Communications
* Interference (communication), anything which alters, modifies, or disrupts a message
* Adjacent-channel interference, caused by extr ...
between two waves traveling in opposite directions. The most common cause of standing waves is the phenomenon of resonance
Resonance describes the phenomenon of increased amplitude that occurs when the frequency of an applied periodic force (or a Fourier component of it) is equal or close to a natural frequency of the system on which it acts. When an oscillatin ...
, in which standing waves occur inside a resonator
A resonator is a device or system that exhibits resonance or resonant behavior. That is, it naturally oscillates with greater amplitude at some frequencies, called resonant frequencies, than at other frequencies. The oscillations in a resonator ...
due to interference between waves reflected back and forth at the resonator's resonant frequency
Resonance describes the phenomenon of increased amplitude that occurs when the frequency of an applied periodic force (or a Fourier component of it) is equal or close to a natural frequency of the system on which it acts. When an oscillatin ...
.
For waves of equal amplitude
The amplitude of a periodic variable is a measure of its change in a single period (such as time or spatial period). The amplitude of a non-periodic signal is its magnitude compared with a reference value. There are various definitions of amplit ...
traveling in opposing directions, there is on average
In ordinary language, an average is a single number taken as representative of a list of numbers, usually the sum of the numbers divided by how many numbers are in the list (the arithmetic mean). For example, the average of the numbers 2, 3, 4, 7, ...
no net propagation of energy.
Moving medium
As an example of the first type, under certain meteorological conditions standing waves form in the atmosphere in thelee
Lee may refer to:
Name
Given name
* Lee (given name), a given name in English
Surname
* Chinese surnames romanized as Li or Lee:
** Li (surname 李) or Lee (Hanzi ), a common Chinese surname
** Li (surname 利) or Lee (Hanzi ), a Chinese ...
of mountain ranges. Such waves are often exploited by glider pilots
Glider may refer to:
Aircraft and transport Aircraft
* Glider (aircraft), heavier-than-air aircraft primarily intended for unpowered flight
** Glider (sailplane), a rigid-winged glider aircraft with an undercarriage, used in the sport of gliding
...
.
Standing waves and hydraulic jump
A hydraulic jump is a phenomenon in the science of hydraulics which is frequently observed in open channel flow such as rivers and spillways. When liquid at high velocity discharges into a zone of lower velocity, a rather abrupt rise occurs in th ...
s also form on fast flowing river rapids and tidal currents such as the Saltstraumen
Saltstraumen is a small strait with one of the strongest tidal currents in the world. It is located in the municipality of Bodø in Nordland county, Norway. It is located about southeast of the town of Bodø. The narrow channel connects the out ...
maelstrom
Maelstrom may refer to:
* Maelstrom (whirlpool), a powerful whirlpool
** originally the Moskstraumen in English
Amusement rides
* Maelstrom (ride), a former log flume dark ride attraction in the Epcot theme park at Walt Disney World Resort ...
. A requirement for this in river currents is a flowing water with shallow depth in which the inertia
Inertia is the idea that an object will continue its current motion until some force causes its speed or direction to change. The term is properly understood as shorthand for "the principle of inertia" as described by Newton in his first law ...
of the water overcomes its gravity
In physics, gravity () is a fundamental interaction which causes mutual attraction between all things with mass or energy. Gravity is, by far, the weakest of the four fundamental interactions, approximately 1038 times weaker than the stro ...
due to the supercritical flow
A supercritical flow is a flow whose velocity is larger than the wave velocity. The analogous condition in gas dynamics is supersonic speed.
According to the website Civil Engineering Terms, supercritical flow is defined as follows:
The flow ...
speed (Froude number
In continuum mechanics, the Froude number (, after William Froude, ) is a dimensionless number defined as the ratio of the flow inertia to the external field (the latter in many applications simply due to gravity). The Froude number is based on t ...
: 1.7 – 4.5, surpassing 4.5 results in direct standing wave) and is therefore neither significantly slowed down by the obstacle nor pushed to the side. Many standing river waves are popular river surfing
River surfing is the sport of surfing either standing waves, tidal bores or upstream waves in rivers. Claims for its origins include a 1955 ride of along the tidal bore of the River Severn.
River surfing on standing waves has been documented a ...
breaks.
Opposing waves
As an example of the second type, a ''standing wave'' in atransmission line
In electrical engineering, a transmission line is a specialized cable or other structure designed to conduct electromagnetic waves in a contained manner. The term applies when the conductors are long enough that the wave nature of the transmis ...
is a wave in which the distribution of current
Currents, Current or The Current may refer to:
Science and technology
* Current (fluid), the flow of a liquid or a gas
** Air current, a flow of air
** Ocean current, a current in the ocean
*** Rip current, a kind of water current
** Current (stre ...
, voltage
Voltage, also known as electric pressure, electric tension, or (electric) potential difference, is the difference in electric potential between two points. In a static electric field, it corresponds to the work needed per unit of charge to m ...
, or field strength In physics, field strength means the ''magnitude'' of a vector-valued field (e.g., in volts per meter, V/m, for an electric field ''E'').
For example, an electromagnetic field results in both electric field strength and magnetic field strength.
As ...
is formed by the superposition of two waves of the same frequency
Frequency is the number of occurrences of a repeating event per unit of time. It is also occasionally referred to as ''temporal frequency'' for clarity, and is distinct from ''angular frequency''. Frequency is measured in hertz (Hz) which is eq ...
propagating in opposite directions. The effect is a series of nodes
In general, a node is a localized swelling (a "knot") or a point of intersection (a Vertex (graph theory), vertex).
Node may refer to:
In mathematics
*Vertex (graph theory), a vertex in a mathematical graph
*Vertex (geometry), a point where two ...
(zero displacement
Displacement may refer to:
Physical sciences
Mathematics and Physics
*Displacement (geometry), is the difference between the final and initial position of a point trajectory (for instance, the center of mass of a moving object). The actual path ...
) and anti-node
A node is a point along a standing wave where the wave has minimum amplitude. For instance, in a vibrating guitar string, the ends of the string are nodes. By changing the position of the end node through frets, the guitarist changes the effec ...
s (maximum displacement
Displacement may refer to:
Physical sciences
Mathematics and Physics
*Displacement (geometry), is the difference between the final and initial position of a point trajectory (for instance, the center of mass of a moving object). The actual path ...
) at fixed points along the transmission line. Such a standing wave may be formed when a wave is transmitted into one end of a transmission line and is reflected from the other end by an impedance mismatch, ''i.e.'', discontinuity, such as an open circuit Open circuit may refer to:
*Open-circuit scuba, a type of SCUBA-diving equipment where the user breathes from the set and then exhales to the surroundings without recycling the exhaled air
*Open-circuit test, a method used in electrical engineering ...
or a short
Short may refer to:
Places
* Short (crater), a lunar impact crater on the near side of the Moon
* Short, Mississippi, an unincorporated community
* Short, Oklahoma, a census-designated place
People
* Short (surname)
* List of people known as ...
. The failure of the line to transfer power at the standing wave frequency will usually result in attenuation distortion
Attenuation distortion is the distortion of an analog signal that occurs during transmission when the transmission medium does not have a flat frequency response across the bandwidth of the medium or the frequency spectrum of the signal.Rowe, Stand ...
.
In practice, losses in the transmission line and other components mean that a perfect reflection and a pure standing wave are never achieved. The result is a ''partial standing wave'', which is a superposition of a standing wave and a traveling wave. The degree to which the wave resembles either a pure standing wave or a pure traveling wave is measured by the standing wave ratio
In radio engineering and telecommunications, standing wave ratio (SWR) is a measure of impedance matching of loads to the characteristic impedance of a transmission line or waveguide. Impedance mismatches result in standing waves along the transmi ...
(SWR).
Another example is standing waves in the open ocean
The ocean (also the sea or the world ocean) is the body of salt water that covers approximately 70.8% of the surface of Earth and contains 97% of Earth's water. An ocean can also refer to any of the large bodies of water into which the wo ...
formed by waves with the same wave period moving in opposite directions. These may form near storm centres, or from reflection of a swell at the shore, and are the source of microbarom In acoustics, microbaroms, also known as the "voice of the sea",
are a class of Earth's atmosphere, atmospheric infrasonic waves generated in marine storms
by a non-linear interaction of ocean surface waves with the atmosphere.
They typically ...
s and microseism
In seismology, a microseism is defined as a faint earth tremor caused by natural phenomena. Sometimes referred to as a "hum", it should not be confused with the anomalous acoustic phenomenon of the same name. The term is most commonly used to ref ...
s.
Mathematical description
This section considers representative one- and two-dimensional cases of standing waves. First, an example of an infinite length string shows how identical waves traveling in opposite directions interfere to produce standing waves. Next, two finite length string examples with differentboundary conditions
In mathematics, in the field of differential equations, a boundary value problem is a differential equation together with a set of additional constraints, called the boundary conditions. A solution to a boundary value problem is a solution to th ...
demonstrate how the boundary conditions restrict the frequencies that can form standing waves. Next, the example of sound waves in a pipe demonstrates how the same principles can be applied to longitudinal waves with analogous boundary conditions.
Standing waves can also occur in two- or three-dimensional resonator
A resonator is a device or system that exhibits resonance or resonant behavior. That is, it naturally oscillates with greater amplitude at some frequencies, called resonant frequencies, than at other frequencies. The oscillations in a resonator ...
s. With standing waves on two-dimensional membranes such as drumhead
A drumhead or drum skin is a membrane stretched over one or both of the open ends of a drum. The drumhead is struck with sticks, mallets, or hands, so that it vibrates and the sound resonates through the drum.
Additionally outside of percus ...
s, illustrated in the animations above, the nodes become nodal lines, lines on the surface at which there is no movement, that separate regions vibrating with opposite phase. These nodal line patterns are called Chladni figure
Ernst Florens Friedrich Chladni (, , ; 30 November 1756 – 3 April 1827) was a German physicist and musician. His most important work, for which he is sometimes labeled as the father of acoustics, included research on vibrating plates and ...
s. In three-dimensional resonators, such as musical instrument sound box
A sound box or sounding box (sometimes written soundbox) is an open chamber in the body of a musical instrument which modifies the sound of the instrument, and helps transfer that sound to the surrounding air. Objects respond more strongly to vibr ...
es and microwave cavity resonator
A resonator is a device or system that exhibits resonance or resonant behavior. That is, it naturally oscillates with greater amplitude at some frequencies, called resonant frequencies, than at other frequencies. The oscillations in a resonator ...
s, there are nodal surfaces. This section includes a two-dimensional standing wave example with a rectangular boundary to illustrate how to extend the concept to higher dimensions.
Standing wave on an infinite length string
To begin, consider a string of infinite length along the ''x''-axis that is free to be stretched transversely in the ''y'' direction. For aharmonic wave
A harmonic is a wave with a frequency that is a positive integer multiple of the ''fundamental frequency'', the frequency of the original periodic signal, such as a sinusoidal wave. The original signal is also called the ''1st harmonic'', the ...
traveling to the right along the string, the string's displacement
Displacement may refer to:
Physical sciences
Mathematics and Physics
*Displacement (geometry), is the difference between the final and initial position of a point trajectory (for instance, the center of mass of a moving object). The actual path ...
in the ''y'' direction as a function of position ''x'' and time ''t'' is
:
The displacement in the ''y''-direction for an identical harmonic wave traveling to the left is
:
where
*''y''max is the amplitude
The amplitude of a periodic variable is a measure of its change in a single period (such as time or spatial period). The amplitude of a non-periodic signal is its magnitude compared with a reference value. There are various definitions of amplit ...
of the displacement of the string for each wave,
*''ω'' is the angular frequency
In physics, angular frequency "''ω''" (also referred to by the terms angular speed, circular frequency, orbital frequency, radian frequency, and pulsatance) is a scalar measure of rotation rate. It refers to the angular displacement per unit tim ...
or equivalently ''2π'' times the frequency
Frequency is the number of occurrences of a repeating event per unit of time. It is also occasionally referred to as ''temporal frequency'' for clarity, and is distinct from ''angular frequency''. Frequency is measured in hertz (Hz) which is eq ...
''f'',
*''λ'' is the wavelength
In physics, the wavelength is the spatial period of a periodic wave—the distance over which the wave's shape repeats.
It is the distance between consecutive corresponding points of the same phase on the wave, such as two adjacent crests, tro ...
of the wave.
For identical right- and left-traveling waves on the same string, the total displacement of the string is the sum of ''y''R and ''y''L,
:
Using the trigonometric sum-to-product identity ,
Note that Equation () does not describe a traveling wave. At any position ''x'', ''y''(''x'',''t'') simply oscillates in time with an amplitude that varies in the ''x''-direction as . The animation at the beginning of this article depicts what is happening. As the left-traveling blue wave and right-traveling green wave interfere, they form the standing red wave that does not travel and instead oscillates in place.
Because the string is of infinite length, it has no boundary condition for its displacement at any point along the ''x''-axis. As a result, a standing wave can form at any frequency.
At locations on the ''x''-axis that are ''even'' multiples of a quarter wavelength,
:
the amplitude is always zero. These locations are called nodes
In general, a node is a localized swelling (a "knot") or a point of intersection (a Vertex (graph theory), vertex).
Node may refer to:
In mathematics
*Vertex (graph theory), a vertex in a mathematical graph
*Vertex (geometry), a point where two ...
. At locations on the ''x''-axis that are ''odd'' multiples of a quarter wavelength
:
the amplitude is maximal, with a value of twice the amplitude of the right- and left-traveling waves that interfere to produce this standing wave pattern. These locations are called anti-node
A node is a point along a standing wave where the wave has minimum amplitude. For instance, in a vibrating guitar string, the ends of the string are nodes. By changing the position of the end node through frets, the guitarist changes the effec ...
s. The distance between two consecutive nodes or anti-nodes is half the wavelength, ''λ''/2.
Standing wave on a string with two fixed ends
Next, consider a string with fixed ends at and . The string will have some damping as it is stretched by traveling waves, but assume the damping is very small. Suppose that at the fixed end a sinusoidal force is applied that drives the string up and down in the y-direction with a small amplitude at some frequency ''f''. In this situation, the driving force produces a right-traveling wave. That wave reflects off the right fixed end and travels back to the left, reflects again off the left fixed end and travels back to the right, and so on. Eventually, a steady state is reached where the string has identical right- and left-traveling waves as in the infinite-length case and the power dissipated by damping in the string equals the power supplied by the driving force so the waves have constant amplitude. Equation () still describes the standing wave pattern that can form on this string, but now Equation () is subject toboundary condition
In mathematics, in the field of differential equations, a boundary value problem is a differential equation together with a set of additional constraints, called the boundary conditions. A solution to a boundary value problem is a solution to th ...
s where at and because the string is fixed at and because we assume the driving force at the fixed end has small amplitude. Checking the values of ''y'' at the two ends,
:
:
 This boundary condition is in the form of the Sturm–Liouville formulation. The latter boundary condition is satisfied when . ''L'' is given, so the boundary condition restricts the wavelength of the standing waves to
:
Waves can only form standing waves on this string if they have a wavelength that satisfies this relationship with ''L''. If waves travel with speed ''v'' along the string, then equivalently the frequency of the standing waves is restricted to
:
The standing wave with oscillates at the
This boundary condition is in the form of the Sturm–Liouville formulation. The latter boundary condition is satisfied when . ''L'' is given, so the boundary condition restricts the wavelength of the standing waves to
:
Waves can only form standing waves on this string if they have a wavelength that satisfies this relationship with ''L''. If waves travel with speed ''v'' along the string, then equivalently the frequency of the standing waves is restricted to
:
The standing wave with oscillates at the fundamental frequency
The fundamental frequency, often referred to simply as the ''fundamental'', is defined as the lowest frequency of a periodic waveform. In music, the fundamental is the musical pitch of a note that is perceived as the lowest partial present. In ...
and has a wavelength that is twice the length of the string. Higher integer values of ''n'' correspond to modes of oscillation called harmonic
A harmonic is a wave with a frequency that is a positive integer multiple of the ''fundamental frequency'', the frequency of the original periodic signal, such as a sinusoidal wave. The original signal is also called the ''1st harmonic'', the ...
s or overtone
An overtone is any resonant frequency above the fundamental frequency of a sound. (An overtone may or may not be a harmonic) In other words, overtones are all pitches higher than the lowest pitch within an individual sound; the fundamental i ...
s. Any standing wave on the string will have ''n'' + 1 nodes including the fixed ends and ''n'' anti-nodes.
To compare this example's nodes to the description of nodes for standing waves in the infinite length string, note that Equation () can be rewritten as
:
:
In this variation of the expression for the wavelength, ''n'' must be even. Cross multiplying we see that because ''L'' is a node, it is an ''even'' multiple of a quarter wavelength,
:
:
This example demonstrates a type of resonance
Resonance describes the phenomenon of increased amplitude that occurs when the frequency of an applied periodic force (or a Fourier component of it) is equal or close to a natural frequency of the system on which it acts. When an oscillatin ...
and the frequencies that produce standing waves can be referred to as ''resonant frequencies''.
Standing wave on a string with one fixed end
 Next, consider the same string of length ''L'', but this time it is only fixed at . At , the string is free to move in the ''y'' direction. For example, the string might be tied at to a ring that can slide freely up and down a pole. The string again has small damping and is driven by a small driving force at .
In this case, Equation () still describes the standing wave pattern that can form on the string, and the string has the same boundary condition of at . However, at where the string can move freely there should be an anti-node with maximal amplitude of ''y''. Equivalently, this boundary condition of the "free end" can be stated as at , which is in the form of the Sturm–Liouville formulation. The intuition for this boundary condition at is that the motion of the "free end" will follow that of the point to its left.
Reviewing Equation (), for the largest amplitude of ''y'' occurs when , or
:
This leads to a different set of wavelengths than in the two-fixed-ends example. Here, the wavelength of the standing waves is restricted to
:
:
Equivalently, the frequency is restricted to
:
Note that in this example ''n'' only takes odd values. Because ''L'' is an anti-node, it is an ''odd'' multiple of a quarter wavelength. Thus the fundamental mode in this example only has one quarter of a complete sine cycle–zero at and the first peak at –the first harmonic has three quarters of a complete sine cycle, and so on.
This example also demonstrates a type of resonance and the frequencies that produce standing waves are called ''resonant frequencies''.
Next, consider the same string of length ''L'', but this time it is only fixed at . At , the string is free to move in the ''y'' direction. For example, the string might be tied at to a ring that can slide freely up and down a pole. The string again has small damping and is driven by a small driving force at .
In this case, Equation () still describes the standing wave pattern that can form on the string, and the string has the same boundary condition of at . However, at where the string can move freely there should be an anti-node with maximal amplitude of ''y''. Equivalently, this boundary condition of the "free end" can be stated as at , which is in the form of the Sturm–Liouville formulation. The intuition for this boundary condition at is that the motion of the "free end" will follow that of the point to its left.
Reviewing Equation (), for the largest amplitude of ''y'' occurs when , or
:
This leads to a different set of wavelengths than in the two-fixed-ends example. Here, the wavelength of the standing waves is restricted to
:
:
Equivalently, the frequency is restricted to
:
Note that in this example ''n'' only takes odd values. Because ''L'' is an anti-node, it is an ''odd'' multiple of a quarter wavelength. Thus the fundamental mode in this example only has one quarter of a complete sine cycle–zero at and the first peak at –the first harmonic has three quarters of a complete sine cycle, and so on.
This example also demonstrates a type of resonance and the frequencies that produce standing waves are called ''resonant frequencies''.
Standing wave in a pipe
Consider a standing wave in a pipe of length ''L''. The air inside the pipe serves as the medium forlongitudinal
Longitudinal is a geometric term of location which may refer to:
* Longitude
** Line of longitude, also called a meridian
* Longitudinal engine, an internal combustion engine in which the crankshaft is oriented along the long axis of the vehicle, ...
sound wave
In physics, sound is a vibration that propagates as an acoustic wave, through a transmission medium such as a gas, liquid or solid.
In human physiology and psychology, sound is the ''reception'' of such waves and their ''perception'' by the ...
s traveling to the right or left through the pipe. While the transverse waves on the string from the previous examples vary in their displacement perpendicular to the direction of wave motion, the waves traveling through the air in the pipe vary in terms of their pressure and longitudinal displacement along the direction of wave motion. The wave propagates by alternately compressing and expanding air in segments of the pipe, which displaces the air slightly from its rest position and transfers energy to neighboring segments through the forces exerted by the alternating high and low air pressures. Equations resembling those for the wave on a string can be written for the change in pressure Δ''p'' due to a right- or left-traveling wave in the pipe.
:
:
where
*''p''max is the pressure amplitude or the maximum increase or decrease in air pressure due to each wave,
*''ω'' is the angular frequency
In physics, angular frequency "''ω''" (also referred to by the terms angular speed, circular frequency, orbital frequency, radian frequency, and pulsatance) is a scalar measure of rotation rate. It refers to the angular displacement per unit tim ...
or equivalently ''2π'' times the frequency
Frequency is the number of occurrences of a repeating event per unit of time. It is also occasionally referred to as ''temporal frequency'' for clarity, and is distinct from ''angular frequency''. Frequency is measured in hertz (Hz) which is eq ...
''f'',
*''λ'' is the wavelength
In physics, the wavelength is the spatial period of a periodic wave—the distance over which the wave's shape repeats.
It is the distance between consecutive corresponding points of the same phase on the wave, such as two adjacent crests, tro ...
of the wave.
If identical right- and left-traveling waves travel through the pipe, the resulting superposition is described by the sum
:
Note that this formula for the pressure is of the same form as Equation (), so a stationary pressure wave forms that is fixed in space and oscillates in time.
If the end of a pipe is closed, the pressure is maximal since the closed end of the pipe exerts a force that restricts the movement of air. This corresponds to a pressure anti-node (which is a node for molecular motions, because the molecules near the closed end can't move). If the end of the pipe is open, the pressure variations are very small, corresponding to a pressure node (which is an anti-node for molecular motions, because the molecules near the open end can move freely). The exact location of the pressure node at an open end is actually slightly beyond the open end of the pipe, so the effective length of the pipe for the purpose of determining resonant frequencies is slightly longer than its physical length. This difference in length is ignored in this example. In terms of reflections, open ends partially reflect waves back into the pipe, allowing some energy to be released into the outside air. Ideally, closed ends reflect the entire wave back in the other direction.
First consider a pipe that is open at both ends, for example an open organ pipe
An organ pipe is a sound-producing element of the pipe organ that resonates at a specific pitch when pressurized air (commonly referred to as ''wind'') is driven through it. Each pipe is tuned to a specific note of the musical scale. A set of ...
or a recorder
Recorder or The Recorder may refer to:
Newspapers
* ''Indianapolis Recorder'', a weekly newspaper
* ''The Recorder'' (Massachusetts newspaper), a daily newspaper published in Greenfield, Massachusetts, US
* ''The Recorder'' (Port Pirie), a news ...
. Given that the pressure must be zero at both open ends, the boundary conditions are analogous to the string with two fixed ends,
:
:
which only occurs when the wavelength of standing waves is
:
:
or equivalently when the frequency is
:
where ''v'' is the speed of sound
The speed of sound is the distance travelled per unit of time by a sound wave as it propagates through an elastic medium. At , the speed of sound in air is about , or one kilometre in or one mile in . It depends strongly on temperature as w ...
.
Next, consider a pipe that is open at (and therefore has a pressure node) and closed at (and therefore has a pressure anti-node). The closed "free end" boundary condition for the pressure at can be stated as , which is in the form of the Sturm–Liouville formulation. The intuition for this boundary condition at is that the pressure of the closed end will follow that of the point to its left. Examples of this setup include a bottle and a clarinet
The clarinet is a musical instrument in the woodwind family. The instrument has a nearly cylindrical bore and a flared bell, and uses a single reed to produce sound.
Clarinets comprise a family of instruments of differing sizes and pitches ...
. This pipe has boundary conditions analogous to the string with only one fixed end. Its standing waves have wavelengths restricted to
:
:
or equivalently the frequency of standing waves is restricted to
:
Note that for the case where one end is closed, ''n'' only takes odd values just like in the case of the string fixed at only one end.
 So far, the wave has been written in terms of its pressure as a function of position ''x'' and time. Alternatively, the wave can be written in terms of its longitudinal displacement of air, where air in a segment of the pipe moves back and forth slightly in the ''x''-direction as the pressure varies and waves travel in either or both directions. The change in pressure Δ''p'' and longitudinal displacement ''s'' are related as
:
where ''ρ'' is the
So far, the wave has been written in terms of its pressure as a function of position ''x'' and time. Alternatively, the wave can be written in terms of its longitudinal displacement of air, where air in a segment of the pipe moves back and forth slightly in the ''x''-direction as the pressure varies and waves travel in either or both directions. The change in pressure Δ''p'' and longitudinal displacement ''s'' are related as
:
where ''ρ'' is the density
Density (volumetric mass density or specific mass) is the substance's mass per unit of volume. The symbol most often used for density is ''ρ'' (the lower case Greek letter rho), although the Latin letter ''D'' can also be used. Mathematical ...
of the air. In terms of longitudinal displacement, closed ends of pipes correspond to nodes since air movement is restricted and open ends correspond to anti-nodes since the air is free to move. A similar, easier to visualize phenomenon occurs in longitudinal waves propagating along a spring.
We can also consider a pipe that is closed at both ends. In this case, both ends will be pressure anti-nodes or equivalently both ends will be displacement nodes. This example is analogous to the case where both ends are open, except the standing wave pattern has a phase shift along the ''x''-direction to shift the location of the nodes and anti-nodes. For example, the longest wavelength that resonates–the fundamental mode–is again twice the length of the pipe, except that the ends of the pipe have pressure anti-nodes instead of pressure nodes. Between the ends there is one pressure node. In the case of two closed ends, the wavelength is again restricted to
:
:
and the frequency is again restricted to
:
A Rubens tube provides a way to visualize the pressure variations of the standing waves in a tube with two closed ends.
2D standing wave with a rectangular boundary
Next, consider transverse waves that can move along a two dimensional surface within a rectangular boundary of length ''Lx'' in the ''x''-direction and length ''Ly'' in the ''y''-direction. Examples of this type of wave are water waves in a pool or waves on a rectangular sheet that has been pulled taut. The waves displace the surface in the ''z''-direction, with defined as the height of the surface when it is still. In two dimensions and Cartesian coordinates, thewave equation
The (two-way) wave equation is a second-order linear partial differential equation for the description of waves or standing wave fields — as they occur in classical physics — such as mechanical waves (e.g. water waves, sound waves and s ...
is
:
where
*''z''(''x'',''y'',''t'') is the displacement of the surface,
*''c'' is the speed of the wave.
To solve this differential equation, let's first solve for its Fourier transform
A Fourier transform (FT) is a mathematical transform that decomposes functions into frequency components, which are represented by the output of the transform as a function of frequency. Most commonly functions of time or space are transformed, ...
, with
:
Taking the Fourier transform of the wave equation,
:
This is an eigenvalue
In linear algebra, an eigenvector () or characteristic vector of a linear transformation is a nonzero vector that changes at most by a scalar factor when that linear transformation is applied to it. The corresponding eigenvalue, often denoted b ...
problem where the frequencies correspond to eigenvalues that then correspond to frequency-specific modes or eigenfunctions. Specifically, this is a form of the Helmholtz equation
In mathematics, the eigenvalue problem for the Laplace operator is known as the Helmholtz equation. It corresponds to the linear partial differential equation
\nabla^2 f = -k^2 f,
where is the Laplace operator (or "Laplacian"), is the eigenv ...
and it can be solved using separation of variables
In mathematics, separation of variables (also known as the Fourier method) is any of several methods for solving ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs ...
. Assume
:
Dividing the Helmholtz equation by ''Z'',
:
This leads to two coupled ordinary differential equations. The ''x'' term equals a constant with respect to ''x'' that we can define as
:
Solving for ''X''(''x''),
:
This ''x''-dependence is sinusoidal–recalling Euler's formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the fundamental relationship between the trigonometric functions and the complex exponential function. Euler's formula states that for an ...
–with constants ''A''''k''''x'' and ''B''''k''''x'' determined by the boundary conditions. Likewise, the ''y'' term equals a constant with respect to ''y'' that we can define as
:
and the dispersion relation
In the physical sciences and electrical engineering, dispersion relations describe the effect of dispersion on the properties of waves in a medium. A dispersion relation relates the wavelength or wavenumber of a wave to its frequency. Given the d ...
for this wave is therefore
:
Solving the differential equation for the ''y'' term,
:
Multiplying these functions together and applying the inverse Fourier transform, ''z''(''x'',''y'',''t'') is a superposition of modes where each mode is the product of sinusoidal functions for ''x'', ''y'', and ''t'',
:
The constants that determine the exact sinusoidal functions depend on the boundary conditions and initial conditions. To see how the boundary conditions apply, consider an example like the sheet that has been pulled taut where ''z''(''x'',''y'',''t'') must be zero all around the rectangular boundary. For the ''x'' dependence, ''z''(''x'',''y'',''t'') must vary in a way that it can be zero at both and for all values of ''y'' and ''t''. As in the one dimensional example of the string fixed at both ends, the sinusoidal function that satisfies this boundary condition is
:
with ''k''''x'' restricted to
:
Likewise, the ''y'' dependence of ''z''(''x'',''y'',''t'') must be zero at both and , which is satisfied by
:
Restricting the wave numbers to these values also restricts the frequencies that resonate to
:
If the initial conditions for ''z''(''x'',''y'',0) and its time derivative ''ż''(''x'',''y'',0) are chosen so the ''t''-dependence is a cosine function, then standing waves for this system take the form
:
:
So, standing waves inside this fixed rectangular boundary oscillate in time at certain resonant frequencies parameterized by the integers ''n'' and ''m''. As they oscillate in time, they do not travel and their spatial variation is sinusoidal in both the ''x''- and ''y''-directions such that they satisfy the boundary conditions. The fundamental mode, and , has a single antinode in the middle of the rectangle. Varying ''n'' and ''m'' gives complicated but predictable two-dimensional patterns of nodes and antinodes inside the rectangle.
Note from the dispersion relation that in certain situations different modes–meaning different combinations of ''n'' and ''m''–may resonate at the same frequency even though they have different shapes for their ''x''- and ''y''-dependence. For example if the boundary is square, , the modes and , and , and and all resonate at
:
Recalling that ''ω'' determines the eigenvalue in the Helmholtz equation above, the number of modes corresponding to each frequency relates to the frequency's multiplicity
Multiplicity may refer to: In science and the humanities
* Multiplicity (mathematics), the number of times an element is repeated in a multiset
* Multiplicity (philosophy), a philosophical concept
* Multiplicity (psychology), having or using multi ...
as an eigenvalue.
Standing wave ratio, phase, and energy transfer
If the two oppositely moving traveling waves are not of the same amplitude, they will not cancel completely at the nodes, the points where the waves are 180° out of phase, so the amplitude of the standing wave will not be zero at the nodes, but merely a minimum.Standing wave ratio
In radio engineering and telecommunications, standing wave ratio (SWR) is a measure of impedance matching of loads to the characteristic impedance of a transmission line or waveguide. Impedance mismatches result in standing waves along the transmi ...
(SWR) is the ratio of the amplitude at the antinode (maximum) to the amplitude at the node (minimum). A pure standing wave will have an infinite SWR. It will also have a constant phase
Phase or phases may refer to:
Science
*State of matter, or phase, one of the distinct forms in which matter can exist
*Phase (matter), a region of space throughout which all physical properties are essentially uniform
* Phase space, a mathematic ...
at any point in space (but it may undergo a 180° inversion every half cycle). A finite, non-zero SWR indicates a wave that is partially stationary and partially travelling. Such waves can be decomposed into a superposition of two waves: a travelling wave component and a stationary wave component. An SWR of one indicates that the wave does not have a stationary component – it is purely a travelling wave, since the ratio of amplitudes is equal to 1.
A pure standing wave does not transfer energy from the source to the destination. However, the wave is still subject to losses in the medium. Such losses will manifest as a finite SWR, indicating a travelling wave component leaving the source to supply the losses. Even though the SWR is now finite, it may still be the case that no energy reaches the destination because the travelling component is purely supplying the losses. However, in a lossless medium, a finite SWR implies a definite transfer of energy to the destination.
Examples
One easy example to understand standing waves is two people shaking either end of ajump rope
A skipping rope (British English) or jump rope (American English) is a tool used in the sport of skipping/jump rope where one or more participants jump over a rope swung so that it passes under their feet and over their heads. There are multi ...
. If they shake in sync the rope can form a regular pattern of waves oscillating up and down, with stationary points along the rope where the rope is almost still (nodes) and points where the arc of the rope is maximum (antinodes).
Acoustic resonance
Standing waves are also observed in physical media such as strings and columns of air. Any waves traveling along the medium will reflect back when they reach the end. This effect is most noticeable in musical instruments where, at various multiples of avibrating string
A vibration in a strings (music), string is a wave. Acoustic resonance#Resonance of a string, Resonance causes a vibrating string to produce a sound with constant frequency, i.e. constant pitch (music), pitch. If the length or tension of the strin ...
or air column
Acoustic resonance is a phenomenon in which an acoustic system amplifies sound waves whose frequency matches one of its own natural frequencies of vibration (its ''resonance frequencies'').
The term "acoustic resonance" is sometimes used to nar ...
's natural frequency
Natural frequency, also known as eigenfrequency, is the frequency at which a system tends to oscillate in the absence of any driving force.
The motion pattern of a system oscillating at its natural frequency is called the normal mode (if all par ...
, a standing wave is created, allowing harmonics
A harmonic is a wave with a frequency that is a positive integer multiple of the ''fundamental frequency'', the frequency of the original periodic signal, such as a sinusoidal wave. The original signal is also called the ''1st harmonic'', the ...
to be identified. Nodes occur at fixed ends and anti-nodes at open ends. If fixed at only one end, only odd-numbered harmonics are available. At the open end of a pipe the anti-node will not be exactly at the end as it is altered by its contact with the air and so end correction
Whenever a wave forms through a medium/object (organ pipe) with a closed/open end, there is a chance of error in the formation of the wave, i.e. it may not actually start from the opening of the object but instead before the opening, thus resulting ...
is used to place it exactly. The density of a string will affect the frequency at which harmonics will be produced; the greater the density the lower the frequency needs to be to produce a standing wave of the same harmonic.
Visible light
Standing waves are also observed in optical media such asoptical waveguides
An optical waveguide is a physical structure that guides electromagnetic waves in the optical spectrum. Common types of optical waveguides include optical fiber waveguides, transparent dielectric waveguides made of plastic and glass, liquid light g ...
and optical cavities An optical cavity, resonating cavity or optical resonator is an arrangement of mirrors or other optical elements that forms a cavity resonator for light waves. Optical cavities are a major component of lasers, surrounding the gain medium and provi ...
. Laser
A laser is a device that emits light through a process of optical amplification based on the stimulated emission of electromagnetic radiation. The word "laser" is an acronym for "light amplification by stimulated emission of radiation". The fir ...
s use optical cavities in the form of a pair of facing mirrors, which constitute a Fabry–Pérot interferometer
In optics, a Fabry–Pérot interferometer (FPI) or etalon is an optical cavity made from two parallel reflecting surfaces (i.e.: thin mirrors). Optical waves can pass through the optical cavity only when they are in resonance with it. It is ...
. The gain medium
The active laser medium (also called gain medium or lasing medium) is the source of optical gain within a laser. The gain results from the stimulated emission of photons through electronic or molecular transitions to a lower energy state from a ...
in the cavity (such as a crystal
A crystal or crystalline solid is a solid material whose constituents (such as atoms, molecules, or ions) are arranged in a highly ordered microscopic structure, forming a crystal lattice that extends in all directions. In addition, macros ...
) emits light coherently, exciting standing waves of light in the cavity. The wavelength of light is very short (in the range of nanometer
330px, Different lengths as in respect to the molecular scale.
The nanometre (international spelling as used by the International Bureau of Weights and Measures; SI symbol: nm) or nanometer (American and British English spelling differences#-re ...
s, 10−9 m) so the standing waves are microscopic in size. One use for standing light waves is to measure small distances, using optical flat
An optical flat is an optical-grade piece of glass lapped and polished to be extremely flat on one or both sides, usually within a few tens of nanometres (billionths of a metre). They are used with a monochromatic light to determine the flatn ...
s.
X-rays
Interference betweenX-ray
An X-ray, or, much less commonly, X-radiation, is a penetrating form of high-energy electromagnetic radiation. Most X-rays have a wavelength ranging from 10 picometers to 10 nanometers, corresponding to frequencies in the range 30&nb ...
beams can form an X-ray standing wave (XSW) field. Because of the short wavelength of X-rays (less than 1 nanometer), this phenomenon can be exploited for measuring atomic-scale events at material surfaces
A surface, as the term is most generally used, is the outermost or uppermost layer of a physical object or space.
Surface or surfaces may also refer to:
Mathematics
*Surface (mathematics), a generalization of a plane which needs not be flat
*Surf ...
. The XSW is generated in the region where an X-ray beam interferes with a diffracted
Diffraction is defined as the interference or bending of waves around the corners of an obstacle or through an aperture into the region of geometrical shadow of the obstacle/aperture. The diffracting object or aperture effectively becomes a s ...
beam from a nearly perfect single crystal
In materials science, a single crystal (or single-crystal solid or monocrystalline solid) is a material in which the crystal lattice of the entire sample is continuous and unbroken to the edges of the sample, with no grain boundaries.RIWD. "Re ...
surface or a reflection from an X-ray mirror. By tuning the crystal geometry or X-ray wavelength, the XSW can be translated in space, causing a shift in the X-ray fluorescence
X-ray fluorescence (XRF) is the emission of characteristic "secondary" (or fluorescent) X-rays from a material that has been excited by being bombarded with high-energy X-rays or gamma rays. The phenomenon is widely used for elemental analysis ...
or photoelectron
The photoelectric effect is the emission of electrons when electromagnetic radiation, such as light, hits a material. Electrons emitted in this manner are called photoelectrons. The phenomenon is studied in condensed matter physics, and solid sta ...
yield from the atoms near the surface. This shift can be analyzed to pinpoint the location of a particular atomic species relative to the underlying crystal structure
In crystallography, crystal structure is a description of the ordered arrangement of atoms, ions or molecules in a crystal, crystalline material. Ordered structures occur from the intrinsic nature of the constituent particles to form symmetric pat ...
or mirror surface. The XSW method has been used to clarify the atomic-scale details of dopants
A dopant, also called a doping agent, is a trace of impurity element that is introduced into a chemical material to alter its original electrical or optical properties. The amount of dopant necessary to cause changes is typically very low. When ...
in semiconductors, atomic and molecular adsorption
Adsorption is the adhesion of atoms, ions or molecules from a gas, liquid or dissolved solid to a surface. This process creates a film of the ''adsorbate'' on the surface of the ''adsorbent''. This process differs from absorption, in which a f ...
on surfaces, and chemical transformations involved in catalysis
Catalysis () is the process of increasing the rate of a chemical reaction by adding a substance known as a catalyst (). Catalysts are not consumed in the reaction and remain unchanged after it. If the reaction is rapid and the catalyst recyc ...
.
Mechanical waves
Standing waves can be mechanically induced into a solid medium using resonance. One easy to understand example is two people shaking either end of a jump rope. If they shake in sync, the rope will form a regular pattern with nodes and antinodes and appear to be stationary, hence the name standing wave. Similarly a cantilever beam can have a standing wave imposed on it by applying a base excitation. In this case the free end moves the greatest distance laterally compared to any location along the beam. Such a device can be used as asensor
A sensor is a device that produces an output signal for the purpose of sensing a physical phenomenon.
In the broadest definition, a sensor is a device, module, machine, or subsystem that detects events or changes in its environment and sends ...
to track changes in frequency
Frequency is the number of occurrences of a repeating event per unit of time. It is also occasionally referred to as ''temporal frequency'' for clarity, and is distinct from ''angular frequency''. Frequency is measured in hertz (Hz) which is eq ...
or phase
Phase or phases may refer to:
Science
*State of matter, or phase, one of the distinct forms in which matter can exist
*Phase (matter), a region of space throughout which all physical properties are essentially uniform
* Phase space, a mathematic ...
of the resonance of the fiber. One application is as a measurement device for dimensional metrology
Dimensional metrology is the science of using physical measurement equipment to quantify the physical size, form, characteristics, and relational distance from any given feature.
History of metrology
Standardized measurements are essential to t ...
.
Seismic waves
Standing surface waves on the Earth are observed as free oscillations of the Earth.Faraday waves
TheFaraday wave
Faraday waves, also known as Faraday ripples, named after Michael Faraday (1791–1867), are nonlinear standing waves that appear on liquids enclosed by a vibrating receptacle. When the vibration frequency exceeds a critical value, the flat hydros ...
is a non-linear standing wave at the air-liquid interface induced by hydrodynamic instability. It can be used as a liquid-based template to assemble microscale materials.
See also
Waves
Electronics
Notes
References
* * *External links
* {{Strings (music) Wave mechanics Articles containing video clips