Speed (finance) on:
[Wikipedia]
[Google]
[Amazon]
In
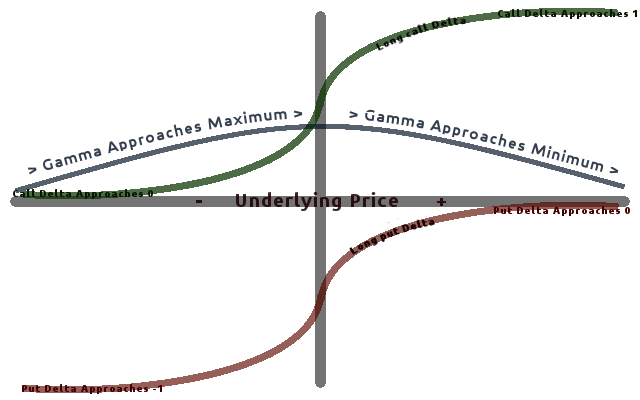 Gamma is greatest approximately at-the-money (ATM) and diminishes the further out you go either in-the-money (ITM) or out-of-the-money (OTM). Gamma is important because it corrects for the
Gamma is greatest approximately at-the-money (ATM) and diminishes the further out you go either in-the-money (ITM) or out-of-the-money (OTM). Gamma is important because it corrects for the
/ref> (sometimes rhova) measures the rate of change in rho with respect to volatility. Vera is the second derivative of the value function; once to volatility and once to interest rate. The word 'Vera' was coined by R. Naryshkin in early 2012 when this sensitivity needed to be used in practice to assess the impact of volatility changes on rho-hedging, but no name yet existed in the available literature. 'Vera' was picked to sound similar to a combination of Vega and Rho, its respective first-order Greeks. This name is now in a wider use, including, for example, the
/ref> which uses quoted call option prices to estimate the Risk-neutral measure, risk-neutral probabilities implied by such prices. For call options, it can be approximated using infinitesimal portfolios of
Vanilla Options - Espen Haug
* Volga, Vanna, Speed, Charm, Color
Vanilla Options - Uwe WystupVanilla Options - Uwe Wystup
Step-by-step mathematical derivations of option Greeks
Derivation of European Vanilla Call Price
Derivation of European Vanilla Call Delta
Derivation of European Vanilla Call Gamma
Derivation of European Vanilla Call Speed
Derivation of European Vanilla Call Vega
Derivation of European Vanilla Call Volga
Derivation of European Vanilla Call Vanna as Derivative of Vega with respect to underlying
Derivation of European Vanilla Call Vanna as Derivative of Delta with respect to volatility
Derivation of European Vanilla Call Theta
Derivation of European Vanilla Call Rho
Derivation of European Vanilla Put Price
Derivation of European Vanilla Put Delta
Derivation of European Vanilla Put Gamma
Derivation of European Vanilla Put Speed
Derivation of European Vanilla Put Vega
Derivation of European Vanilla Put Volga
Derivation of European Vanilla Put Vanna as Derivative of Vega with respect to underlying
Derivation of European Vanilla Put Vanna as Derivative of Delta with respect to volatility
Derivation of European Vanilla Put Theta
Derivation of European Vanilla Put Rho
Online tools
Surface Plots of Black-Scholes Greeks
Chris Murray
Online real-time option prices and Greeks calculator when the underlying is normally distributed
Razvan Pascalau, Univ. of Alabama
R package to compute Greeks for European-, American- and Asian Options {{DEFAULTSORT:Greeks (Finance) Mathematical finance Financial ratios Options (finance)
mathematical finance
Mathematical finance, also known as quantitative finance and financial mathematics, is a field of applied mathematics, concerned with mathematical modeling of financial markets.
In general, there exist two separate branches of finance that require ...
, the Greeks are the quantities representing the sensitivity of the price of derivatives
The derivative of a function is the rate of change of the function's output relative to its input value.
Derivative may also refer to:
In mathematics and economics
* Brzozowski derivative in the theory of formal languages
* Formal derivative, an ...
such as options
Option or Options may refer to:
Computing
*Option key, a key on Apple computer keyboards
*Option type, a polymorphic data type in programming languages
* Command-line option, an optional parameter to a command
*OPTIONS, an HTTP request method
...
to a change in underlying parameter
A parameter (), generally, is any characteristic that can help in defining or classifying a particular system (meaning an event, project, object, situation, etc.). That is, a parameter is an element of a system that is useful, or critical, when ...
s on which the value of an instrument or portfolio of financial instrument
Financial instruments are monetary contracts between parties. They can be created, traded, modified and settled. They can be cash (currency), evidence of an ownership interest in an entity or a contractual right to receive or deliver in the form ...
s is dependent. The name is used because the most common of these sensitivities are denoted by Greek letters (as are some other finance measures). Collectively these have also been called the risk sensitivities, risk measures or hedge parameters.
Use of the Greeks
The Greeks are vital tools in risk management. Each Greek measures the sensitivity of the value of a portfolio to a small change in a given underlying parameter, so that component risks may be treated in isolation, and the portfolio rebalanced accordingly to achieve a desired exposure; see for exampledelta hedging In finance, delta neutral describes a portfolio of related financial securities, in which the portfolio value remains unchanged when small changes occur in the value of the underlying security. Such a portfolio typically contains options and their ...
.
The Greeks in the Black–Scholes model are relatively easy to calculate, a desirable property of financial
Finance is the study and discipline of money, currency and capital assets. It is related to, but not synonymous with economics, the study of production, distribution, and consumption of money, assets, goods and services (the discipline of fina ...
models
A model is an informative representation of an object, person or system. The term originally denoted the plans of a building in late 16th-century English, and derived via French and Italian ultimately from Latin ''modulus'', a measure.
Models c ...
, and are very useful for derivatives traders, especially those who seek to hedge their portfolios from adverse changes in market conditions. For this reason, those Greeks which are particularly useful for hedging—such as delta, theta, and vega—are well-defined for measuring changes in Price, Time and Volatility. Although rho is a primary input into the Black–Scholes model, the overall impact on the value of an option corresponding to changes in the risk-free interest rate is generally insignificant and therefore higher-order derivatives involving the risk-free interest rate are not common.
The most common of the Greeks are the first order derivatives: delta
Delta commonly refers to:
* Delta (letter) (Δ or δ), a letter of the Greek alphabet
* River delta, at a river mouth
* D (NATO phonetic alphabet: "Delta")
* Delta Air Lines, US
* Delta variant of SARS-CoV-2 that causes COVID-19
Delta may also re ...
, vega
Vega is the brightest star in the northern constellation of Lyra. It has the Bayer designation α Lyrae, which is Latinised to Alpha Lyrae and abbreviated Alpha Lyr or α Lyr. This star is relatively close at only from the Sun, an ...
, theta
Theta (, ; uppercase: Θ or ; lowercase: θ or ; grc, ''thē̂ta'' ; Modern: ''thī́ta'' ) is the eighth letter of the Greek alphabet, derived from the Phoenician letter Teth . In the system of Greek numerals, it has a value of 9.
Gr ...
and rho
Rho (uppercase Ρ, lowercase ρ or ; el, ρο or el, ρω, label=none) is the 17th letter of the Greek alphabet. In the system of Greek numerals it has a value of 100. It is derived from Phoenician letter res . Its uppercase form uses the sa ...
as well as gamma
Gamma (uppercase , lowercase ; ''gámma'') is the third letter of the Greek alphabet. In the system of Greek numerals it has a value of 3. In Ancient Greek, the letter gamma represented a voiced velar stop . In Modern Greek, this letter re ...
, a second-order derivative of the value function. The remaining sensitivities in this list are common enough that they have common names, but this list is by no means exhaustive.
Names
The use of Greek letter names is presumably by extension from the common finance termsalpha
Alpha (uppercase , lowercase ; grc, ἄλφα, ''álpha'', or ell, άλφα, álfa) is the first letter of the Greek alphabet. In the system of Greek numerals, it has a value of one. Alpha is derived from the Phoenician letter aleph , whic ...
and beta
Beta (, ; uppercase , lowercase , or cursive ; grc, βῆτα, bē̂ta or ell, βήτα, víta) is the second letter of the Greek alphabet. In the system of Greek numerals, it has a value of 2. In Modern Greek, it represents the voiced labiod ...
, and the use of sigma
Sigma (; uppercase Σ, lowercase σ, lowercase in word-final position ς; grc-gre, σίγμα) is the eighteenth letter of the Greek alphabet. In the system of Greek numerals, it has a value of 200. In general mathematics, uppercase Σ is used as ...
(the standard deviation of logarithmic returns) and tau
Tau (uppercase Τ, lowercase τ, or \boldsymbol\tau; el, ταυ ) is the 19th letter of the Greek alphabet, representing the voiceless dental or alveolar plosive . In the system of Greek numerals, it has a value of 300.
The name in English ...
(time to expiry) in the Black–Scholes option pricing model. Several names such as 'vega' and 'zomma' are invented, but sound similar to Greek letters. The names 'color' and 'charm' presumably derive from the use of these terms for exotic properties of quarks
A quark () is a type of elementary particle and a fundamental constituent of matter. Quarks combine to form composite particles called hadrons, the most stable of which are protons and neutrons, the components of atomic nuclei. All commonly o ...
in particle physics
Particle physics or high energy physics is the study of fundamental particles and forces that constitute matter and radiation. The fundamental particles in the universe are classified in the Standard Model as fermions (matter particles) an ...
.
First-order Greeks
Delta
Delta
Delta commonly refers to:
* Delta (letter) (Δ or δ), a letter of the Greek alphabet
* River delta, at a river mouth
* D (NATO phonetic alphabet: "Delta")
* Delta Air Lines, US
* Delta variant of SARS-CoV-2 that causes COVID-19
Delta may also re ...
, , measures the rate of change of the theoretical option value with respect to changes in the underlying asset's price. Delta is the first derivative
In mathematics, the derivative of a function of a real variable measures the sensitivity to change of the function value (output value) with respect to a change in its argument (input value). Derivatives are a fundamental tool of calculus. F ...
of the value of the option with respect to the underlying instrument's price .
Practical use
For a vanilla option, delta will be a number between 0.0 and 1.0 for a long call (or a short put) and 0.0 and −1.0 for a long put (or a short call); depending on price, a call option behaves as if one owns 1 share of the underlying stock (if deep in the money), or owns nothing (if far out of the money), or something in between, and conversely for a put option. The difference between the delta of a call and the delta of a put at the same strike is equal to one. By put–call parity, long a call and short a put is equivalent to a forward ''F'', which is linear in the spot ''S,'' with unit factor, so the derivative dF/dS is 1. See the formulas below. These numbers are commonly presented as a percentage of the total number of shares represented by the option contract(s). This is convenient because the option will (instantaneously) behave like the number of shares indicated by the delta. For example, if a portfolio of 100 American call options on XYZ each have a delta of 0.25 (=25%), it will gain or lose value just like 2,500 shares of XYZ as the price changes for small price movements (100 option contracts covers 10,000 shares). The sign and percentage are often dropped – the sign is implicit in the option type (negative for put, positive for call) and the percentage is understood. The most commonly quoted are 25 delta put, 50 delta put/50 delta call, and 25 delta call. 50 Delta put and 50 Delta call are not quite identical, due to spot and forward differing by the discount factor, but they are often conflated. Delta is always positive for long calls and negative for long puts (unless they are zero). The total delta of a complex portfolio of positions on the same underlying asset can be calculated by simply taking the sum of the deltas for each individual position – delta of a portfolio is linear in the constituents. Since the delta of underlying asset is always 1.0, the trader could delta-hedge his entire position in the underlying by buying or shorting the number of shares indicated by the total delta. For example, if the delta of a portfolio of options in XYZ (expressed as shares of the underlying) is +2.75, the trader would be able to delta-hedge the portfolio byselling short
In finance, being short in an asset means investing in such a way that the investor will profit if the value of the asset falls. This is the opposite of a more conventional "long" position, where the investor will profit if the value of the ...
2.75 shares of the underlying. This portfolio will then retain its total value regardless of which direction the price of XYZ moves. (Albeit for only small movements of the underlying, a short amount of time and not-withstanding changes in other market conditions such as volatility and the rate of return for a risk-free investment).
As a proxy for probability
The (absolute value of) Delta is close to, but not identical with, the percent moneyness of an option, i.e., the ''implied'' probability that the option will expire in-the-money (if the market moves under Brownian motion in the risk-neutral measure). For this reason some option traders use the absolute value of delta as an approximation for percent moneyness. For example, if anout-of-the-money
In finance, moneyness is the relative position of the current price (or future price) of an underlying asset (e.g., a stock) with respect to the strike price of a derivative, most commonly a call option or a put option. Moneyness is firstly a thr ...
call option has a delta of 0.15, the trader might estimate that the option has approximately a 15% chance of expiring in-the-money. Similarly, if a put contract has a delta of −0.25, the trader might expect the option to have a 25% probability of expiring in-the-money. At-the-money
In finance, moneyness is the relative position of the current price (or future price) of an underlying asset (e.g., a stock) with respect to the strike price of a derivative, most commonly a call option or a put option. Moneyness is firstly a thr ...
calls and puts have a delta of approximately 0.5 and −0.5 respectively with a slight bias towards higher deltas for ATM calls. The actual probability of an option finishing in the money is its dual delta
Dual or Duals may refer to:
Paired/two things
* Dual (mathematics), a notion of paired concepts that mirror one another
** Dual (category theory), a formalization of mathematical duality
*** see more cases in :Duality theories
* Dual (grammati ...
, which is the first derivative of option price with respect to strike.
Relationship between call and put delta
Given a European call and put option for the same underlying, strike price and time to maturity, and with no dividend yield, the sum of the absolute values of the delta of each option will be 1 – more precisely, the delta of the call (positive) minus the delta of the put (negative) equals 1. This is due to put–call parity: a long call plus a short put (a call minus a put) replicates a forward, which has delta equal to 1. If the value of delta for an option is known, one can calculate the value of the delta of the option of the same strike price, underlying and maturity but opposite right by subtracting 1 from a known call delta or adding 1 to a known put delta. , therefore: and . For example, if the delta of a call is 0.42 then one can compute the delta of the corresponding put at the same strike price by 0.42 − 1 = −0.58. To derive the delta of a call from a put, one can similarly take −0.58 and add 1 to get 0.42.Vega
Vega measures sensitivity to volatility. Vega is the derivative of the option value with respect to the volatility of the underlying asset. ''Vega'' is not the name of any Greek letter. The glyph used is a non-standard majuscule version of the Greek letter ''nu'' (), written as . Presumably the name ''vega'' was adopted because the Greek letter ''nu'' looked like a Latin ''vee'', and ''vega'' was derived from ''vee'' by analogy with how ''beta'', ''eta'', and ''theta'' are pronounced in American English. The symbolkappa
Kappa (uppercase Κ, lowercase κ or cursive ; el, κάππα, ''káppa'') is the 10th letter of the Greek alphabet, representing the voiceless velar plosive sound in Ancient and Modern Greek. In the system of Greek numerals, has a value o ...
, , is sometimes used (by academics) instead of vega (as is tau ()
or capital lambda
Lambda (}, ''lám(b)da'') is the 11th letter of the Greek alphabet, representing the voiced alveolar lateral approximant . In the system of Greek numerals, lambda has a value of 30. Lambda is derived from the Phoenician Lamed . Lambda gave rise ...
(),
though these are rare).
Vega is typically expressed as the amount of money per underlying share that the option's value will gain or lose as volatility rises or falls by 1 percentage point
A percentage point or percent point is the unit (measurement), unit for the Difference (mathematics), arithmetic difference between two percentages. For example, moving up from 40 percent to 44 percent is an increase of 4 percentage points, but a ...
. All options (both calls and puts) will gain value with rising volatility.
Vega can be an important Greek to monitor for an option trader, especially in volatile markets, since the value of some option strategies can be particularly sensitive to changes in volatility. The value of an at-the-money option straddle, for example, is extremely dependent on changes to volatility.
Theta
Theta
Theta (, ; uppercase: Θ or ; lowercase: θ or ; grc, ''thē̂ta'' ; Modern: ''thī́ta'' ) is the eighth letter of the Greek alphabet, derived from the Phoenician letter Teth . In the system of Greek numerals, it has a value of 9.
Gr ...
, , measures the sensitivity of the value of the derivative to the passage of time (see Option time value): the "time decay."
The mathematical result of the formula for theta (see below) is expressed in value per year. By convention, it is usual to divide the result by the number of days in a year, to arrive at the amount an option's price will drop, in relation to the underlying stock's price. Theta is almost always negative for long calls and puts, and positive for short (or written) calls and puts. An exception is a deep in-the-money European put. The total theta for a portfolio of options can be determined by summing the thetas for each individual position.
The value of an option can be analysed into two parts: the intrinsic value and the time value. The intrinsic value is the amount of money you would gain if you exercised the option immediately, so a call with strike $50 on a stock with price $60 would have intrinsic value of $10, whereas the corresponding put would have zero intrinsic value. The time value is the value of having the option of waiting longer before deciding to exercise. Even a deeply out of the money put will be worth something, as there is some chance the stock price will fall below the strike before the expiry date. However, as time approaches maturity, there is less chance of this happening, so the time value of an option is decreasing with time. Thus if you are long an option you are short theta: your portfolio will lose value with the passage of time (all other factors held constant).
Rho
Rho
Rho (uppercase Ρ, lowercase ρ or ; el, ρο or el, ρω, label=none) is the 17th letter of the Greek alphabet. In the system of Greek numerals it has a value of 100. It is derived from Phoenician letter res . Its uppercase form uses the sa ...
, , measures sensitivity to the interest rate: it is the derivative of the option value with respect to the risk-free interest rate (for the relevant outstanding term).
Except under extreme circumstances, the value of an option is less sensitive to changes in the risk-free interest rate than to changes in other parameters. For this reason, rho is the least used of the first-order Greeks.
Rho is typically expressed as the amount of money, per share of the underlying, that the value of the option will gain or lose as the risk-free interest rate rises or falls by 1.0% per annum (100 basis points).
Lambda
Lambda
Lambda (}, ''lám(b)da'') is the 11th letter of the Greek alphabet, representing the voiced alveolar lateral approximant . In the system of Greek numerals, lambda has a value of 30. Lambda is derived from the Phoenician Lamed . Lambda gave rise ...
, , omega
Omega (; capital: Ω, lowercase: ω; Ancient Greek ὦ, later ὦ μέγα, Modern Greek ωμέγα) is the twenty-fourth and final letter in the Greek alphabet. In the Greek numeric system/isopsephy (gematria), it has a value of 800. The wo ...
, , or elasticity is the percentage
In mathematics, a percentage (from la, per centum, "by a hundred") is a number or ratio expressed as a fraction of 100. It is often denoted using the percent sign, "%", although the abbreviations "pct.", "pct" and sometimes "pc" are also us ...
change in option value per percentage change in the underlying price, a measure of leverage
Leverage or leveraged may refer to:
*Leverage (mechanics), mechanical advantage achieved by using a lever
* ''Leverage'' (album), a 2012 album by Lyriel
*Leverage (dance), a type of dance connection
*Leverage (finance), using given resources to ...
, sometimes called gearing.
It holds that .
Epsilon
Epsilon
Epsilon (, ; uppercase , lowercase or lunate ; el, έψιλον) is the fifth letter of the Greek alphabet, corresponding phonetically to a mid front unrounded vowel or . In the system of Greek numerals it also has the value five. It was der ...
, (also known as psi, ), is the percentage change in option value per percentage
In mathematics, a percentage (from la, per centum, "by a hundred") is a number or ratio expressed as a fraction of 100. It is often denoted using the percent sign, "%", although the abbreviations "pct.", "pct" and sometimes "pc" are also us ...
change in the underlying dividend
A dividend is a distribution of profits by a corporation to its shareholders. When a corporation earns a profit or surplus, it is able to pay a portion of the profit as a dividend to shareholders. Any amount not distributed is taken to be re-in ...
yield, a measure of the dividend risk. The dividend yield impact is in practice determined using a 10% increase in those yields. Obviously, this sensitivity can only be applied to derivative instruments of equity
Equity may refer to:
Finance, accounting and ownership
* Equity (finance), ownership of assets that have liabilities attached to them
** Stock, equity based on original contributions of cash or other value to a business
** Home equity, the dif ...
products.
Second-order Greeks
Gamma
Gamma
Gamma (uppercase , lowercase ; ''gámma'') is the third letter of the Greek alphabet. In the system of Greek numerals it has a value of 3. In Ancient Greek, the letter gamma represented a voiced velar stop . In Modern Greek, this letter re ...
, , measures the rate of change in the delta with respect to changes in the underlying price. Gamma is the second derivative
In mathematics, the derivative of a function of a real variable measures the sensitivity to change of the function value (output value) with respect to a change in its argument (input value). Derivatives are a fundamental tool of calculus. F ...
of the value function with respect to the underlying price.
Most long options have positive gamma and most short options have negative gamma. Long options have a positive relationship with gamma because as price increases, Gamma increases as well, causing Delta to approach 1 from 0 (long call option) and 0 from −1 (long put option). The inverse is true for short options. Gamma is greatest approximately at-the-money (ATM) and diminishes the further out you go either in-the-money (ITM) or out-of-the-money (OTM). Gamma is important because it corrects for the
Gamma is greatest approximately at-the-money (ATM) and diminishes the further out you go either in-the-money (ITM) or out-of-the-money (OTM). Gamma is important because it corrects for the convexity
Convex or convexity may refer to:
Science and technology
* Convex lens, in optics
Mathematics
* Convex set, containing the whole line segment that joins points
** Convex polygon, a polygon which encloses a convex set of points
** Convex polytope, ...
of value.
When a trader seeks to establish an effective delta-hedge for a portfolio, the trader may also seek to neutralize the portfolio's gamma, as this will ensure that the hedge will be effective over a wider range of underlying price movements.
Vanna
Vanna, also referred to as DvegaDspot and DdeltaDvol, is a second order derivative of the option value, once to the underlying spot price and once to volatility. It is mathematically equivalent to DdeltaDvol, the sensitivity of the option delta with respect to change in volatility; or alternatively, the partial of vega with respect to the underlying instrument's price. Vanna can be a useful sensitivity to monitor when maintaining a delta- or vega-hedged portfolio as vanna will help the trader to anticipate changes to the effectiveness of a delta-hedge as volatility changes or the effectiveness of a vega-hedge against change in the underlying spot price. If the underlying value has continuous second partial derivatives, then ,Charm
Charm or delta decay measures the instantaneous rate of change of delta over the passage of time. Charm has also been called DdeltaDtime. Charm can be an important Greek to measure/monitor when delta-hedging a position over a weekend. Charm is a second-order derivative of the option value, once to price and once to the passage of time. It is also then the derivative oftheta
Theta (, ; uppercase: Θ or ; lowercase: θ or ; grc, ''thē̂ta'' ; Modern: ''thī́ta'' ) is the eighth letter of the Greek alphabet, derived from the Phoenician letter Teth . In the system of Greek numerals, it has a value of 9.
Gr ...
with respect to the underlying's price.
The mathematical result of the formula for charm (see below) is expressed in delta/year. It is often useful to divide this by the number of days per year to arrive at the delta decay per day. This use is fairly accurate when the number of days remaining until option expiration is large. When an option nears expiration, charm itself may change quickly, rendering full day estimates of delta decay inaccurate.
Vomma
Vomma, volga, vega convexity, or DvegaDvol measures second order sensitivity to volatility. Vomma is the second derivative of the option value with respect to the volatility, or, stated another way, vomma measures the rate of change to vega as volatility changes. With positive vomma, a position will become long vega as implied volatility increases and short vega as it decreases, which can be scalped in a way analogous to long gamma. And an initially vega-neutral, long-vomma position can be constructed from ratios of options at different strikes. Vomma is positive for long options away from the money, and initially increases with distance from the money (but drops off as vega drops off). (Specifically, vomma is positive where the usual d1 and d2 terms are of the same sign, which is true when d1 < 0 or d2 > 0.)Veta
Veta or DvegaDtime measures the rate of change in the vega with respect to the passage of time. Veta is the second derivative of the value function; once to volatility and once to time. It is common practice to divide the mathematical result of veta by 100 times the number of days per year to reduce the value to the percentage change in vega per one day.Vera
VeraDerivatives – Second-Order Greeks – The Financial Encyclopedia/ref> (sometimes rhova) measures the rate of change in rho with respect to volatility. Vera is the second derivative of the value function; once to volatility and once to interest rate. The word 'Vera' was coined by R. Naryshkin in early 2012 when this sensitivity needed to be used in practice to assess the impact of volatility changes on rho-hedging, but no name yet existed in the available literature. 'Vera' was picked to sound similar to a combination of Vega and Rho, its respective first-order Greeks. This name is now in a wider use, including, for example, the
Maple
''Acer'' () is a genus of trees and shrubs commonly known as maples. The genus is placed in the family Sapindaceae.Stevens, P. F. (2001 onwards). Angiosperm Phylogeny Website. Version 9, June 2008 nd more or less continuously updated since http ...
computer algebra software (which has 'BlackScholesVera' function in its Finance package).
Second order partial derivative with respect to strike K
This partial derivative has a fundamental role in the Breeden-Litzenberger formula,Breeden, Litzenberger, Prices of State-Contingent Claims Implicit in Option Price/ref> which uses quoted call option prices to estimate the Risk-neutral measure, risk-neutral probabilities implied by such prices. For call options, it can be approximated using infinitesimal portfolios of
butterfly
Butterflies are insects in the macrolepidopteran clade Rhopalocera from the Order (biology), order Lepidoptera, which also includes moths. Adult butterflies have large, often brightly coloured wings, and conspicuous, fluttering flight. The ...
strategies.
Third-order Greeks
Speed
Speed measures the rate of change in Gamma with respect to changes in the underlying price. This is also sometimes referred to as the gamma of the gamma or DgammaDspot. Speed is the third derivative of the value function with respect to the underlying spot price. Speed can be important to monitor when delta-hedging or gamma-hedging a portfolio.Zomma
Zomma measures the rate of change of gamma with respect to changes in volatility. Zomma has also been referred to as DgammaDvol. Zomma is the third derivative of the option value, twice to underlying asset price and once to volatility. Zomma can be a useful sensitivity to monitor when maintaining a gamma-hedged portfolio as zomma will help the trader to anticipate changes to the effectiveness of the hedge as volatility changes.Color
Color, gamma decay or DgammaDtime measures the rate of change of gamma over the passage of time. Color is a third-order derivative of the option value, twice to underlying asset price and once to time. Color can be an important sensitivity to monitor when maintaining a gamma-hedged portfolio as it can help the trader to anticipate the effectiveness of the hedge as time passes. The mathematical result of the formula for color (see below) is expressed in gamma per year. It is often useful to divide this by the number of days per year to arrive at the change in gamma per day. This use is fairly accurate when the number of days remaining until option expiration is large. When an option nears expiration, color itself may change quickly, rendering full day estimates of gamma change inaccurate.Ultima
Ultima measures the sensitivity of the option vomma with respect to change in volatility. Ultima has also been referred to as DvommaDvol. Ultima is a third-order derivative of the option value to volatility.Greeks for multi-asset options
If the value of a derivative is dependent on two or more underlyings, its Greeks are extended to include the cross-effects between the underlyings. Correlation delta measures the sensitivity of the derivative's value to a change in the correlation between the underlyings. It is also commonly known as cega. Cross gamma measures the rate of change of delta in one underlying to a change in the level of another underlying. Cross vanna measures the rate of change of vega in one underlying due to a change in the level of another underlying. Equivalently, it measures the rate of change of delta in the second underlying due to a change in the volatility of the first underlying. Cross volga measures the rate of change of vega in one underlying to a change in the volatility of another underlying.Formulas for European option Greeks
The Greeks ofEuropean options
European, or Europeans, or Europeneans, may refer to:
In general
* ''European'', an adjective referring to something of, from, or related to Europe
** Ethnic groups in Europe
** Demographics of Europe
** European cuisine, the cuisines of Europe ...
(calls
Call or Calls may refer to:
Arts, entertainment, and media Games
* Call, a type of betting in poker
* Call, in the game of contract bridge, a bid, pass, double, or redouble in the bidding stage
Music and dance
* Call (band), from Lahore, Paki ...
and puts) under the Black–Scholes model are calculated as follows, where (phi) is the standard normal probability density function
In probability theory, a probability density function (PDF), or density of a continuous random variable, is a function whose value at any given sample (or point) in the sample space (the set of possible values taken by the random variable) can ...
and is the standard normal cumulative distribution function
In probability theory and statistics, the cumulative distribution function (CDF) of a real-valued random variable X, or just distribution function of X, evaluated at x, is the probability that X will take a value less than or equal to x.
Ev ...
. Note that the gamma and vega formulas are the same for calls and puts.
For a given:
* Stock price ,
* Strike price ,
* Risk-free rate ,
* Annual dividend yield ,
* Time to maturity (represented as a unit-less fraction of one year), and
* Volatility .
where
:
Under the Black model
The Black model (sometimes known as the Black-76 model) is a variant of the Black–Scholes option pricing model. Its primary applications are for pricing options on future contracts, bond options, interest rate cap and floors, and swaptions. It w ...
(commonly used for commodities and options on futures) the Greeks can be calculated as follows:
where
:
(*) It can be shown that
Micro proof:
let Then we have: So
Related measures
Some related risk measures offinancial instrument
Financial instruments are monetary contracts between parties. They can be created, traded, modified and settled. They can be cash (currency), evidence of an ownership interest in an entity or a contractual right to receive or deliver in the form ...
s are listed below.
Bond duration and convexity
In trading bonds and otherfixed income securities
Fixed income refers to any type of investment under which the borrower or issuer is obliged to make payments of a fixed amount on a fixed schedule. For example, the borrower may have to pay interest at a fixed rate once a year and repay the prin ...
, various measures of bond duration
In finance, the duration of a financial asset that consists of fixed cash flows, such as a bond, is the weighted average of the times until those fixed cash flows are received.
When the price of an asset is considered as a function of yield, dur ...
are used analogously to the delta of an option. The closest analogue to the delta is DV01
In finance, the duration of a financial asset that consists of fixed cash flows, such as a bond, is the weighted average of the times until those fixed cash flows are received.
When the price of an asset is considered as a function of yield, du ...
, which is the reduction in price (in currency units) for an increase of one basis point
A basis point (often abbreviated as bp, often pronounced as "bip" or "beep") is one hundredth of 1 percentage point. The related term ''permyriad'' means one hundredth of 1 percent. Changes of interest rates are often stated in basis points. If ...
(i.e. 0.01% per annum) in the yield (the yield is the underlying variable).
See also .
Analogous to the lambda is the modified duration
Modified may refer to:
* ''Modified'' (album), the second full-length album by Save Ferris
*Modified racing, or "Modifieds", an American automobile racing genre
See also
* Modification (disambiguation)
* Modifier (disambiguation)
Modifier may re ...
, which is the ''percentage'' change in the market price of the bond(s) for a ''unit'' change in the yield (i.e. it is equivalent to DV01 divided by the market price). Unlike the lambda, which is an elasticity
Elasticity often refers to:
*Elasticity (physics), continuum mechanics of bodies that deform reversibly under stress
Elasticity may also refer to:
Information technology
* Elasticity (data store), the flexibility of the data model and the cl ...
(a percentage change in output for a percentage change in input), the modified duration is instead a ''semi''-elasticity—a percentage change in output for a ''unit'' change in input.
See also Key rate duration
Fixed-income attribution is the process of measuring returns generated by various sources of risk in a fixed income portfolio, particularly when multiple sources of return are active at the same time.
For example, the risks affecting the return ...
.
Bond convexity
In finance, bond convexity is a measure of the non-linear relationship of bond prices to changes in interest rates, the second derivative of the price of the bond with respect to interest rates (duration is the first derivative). In general, the h ...
is a measure of the sensitivity of the duration to changes in interest rate
An interest rate is the amount of interest due per period, as a proportion of the amount lent, deposited, or borrowed (called the principal sum). The total interest on an amount lent or borrowed depends on the principal sum, the interest rate, th ...
s, the second derivative of the price of the bond with respect to interest rates (duration is the first derivative); it is then analogous to gamma. In general, the higher the convexity, the more sensitive the bond price is to the change in interest rates. Bond convexity is one of the most basic and widely used forms of convexity in finance.
For a bond with an embedded option
An embedded option is a component of a financial bond or other security, which provides the bondholder or the issuer the right to take some action against the other party. There are several types of options that can be embedded into a bond; common ...
, the standard yield to maturity based calculations here do not consider how changes in interest rates will alter the cash flows due to option exercise. To address this, effective duration
In finance, the duration of a financial asset that consists of fixed cash flows, such as a bond, is the weighted average of the times until those fixed cash flows are received.
When the price of an asset is considered as a function of yield, du ...
and effective convexity
In finance, bond convexity is a measure of the non-linear relationship of bond prices to changes in interest rates, the second derivative of the price of the bond with respect to interest rates ( duration is the first derivative). In general, the ...
are introduced. These values are typically calculated using a tree-based model, built for the entire yield curve (as opposed to a single yield to maturity), and therefore capturing exercise behavior at each point in the option's life as a function of both time and interest rates; see .
Beta
The beta (β) of astock
In finance, stock (also capital stock) consists of all the shares by which ownership of a corporation or company is divided.Longman Business English Dictionary: "stock - ''especially AmE'' one of the shares into which ownership of a company ...
or portfolio is a number describing the volatility of an asset in relation to the volatility of the benchmark that said asset is being compared to. This benchmark is generally the overall financial market and is often estimated via the use of representative indices, such as the S&P 500
The Standard and Poor's 500, or simply the S&P 500, is a stock market index tracking the stock performance of 500 large companies listed on stock exchanges in the United States. It is one of the most commonly followed equity indices. As of D ...
.
An asset has a Beta of zero if its returns change independently of changes in the market's returns. A positive beta means that the asset's returns generally follow the market's returns, in the sense that they both tend to be above their respective averages together, or both tend to be below their respective averages together. A negative beta means that the asset's returns generally move opposite the market's returns: one will tend to be above its average when the other is below its average.
Fugit
Thefugit
In mathematical finance, fugit is the expected (or optimal) date to exercise an American- or Bermudan option. It is useful for hedging purposes here; see Greeks (finance) and . The term was first introduced by Mark Garman in an article "Sempe ...
is the expected time to exercise an American or Bermudan option. Fugit is usefully computed for hedging purposes — for example, one can represent flows of an American swaption
A swaption is an option granting its owner the right but not the obligation to enter into an underlying swap. Although options can be traded on a variety of swaps, the term "swaption" typically refers to options on interest rate swaps.
Types of ...
like the flows of a swap starting at the fugit multiplied by delta, and then use these to compute other sensitivities.
See also
*Alpha (finance)
Alpha is a measure of the active return on an investment, the performance of that investment compared with a suitable market index. An alpha of 1% means the investment's return on investment over a selected period of time was 1% better than the ma ...
* Beta (finance)
* Delta neutral
* Financial risk management
Financial risk management is the practice of protecting economic value in a firm by using financial instruments to manage exposure to financial risk - principally operational risk, credit risk and market risk, with more specific variants as liste ...
* Greek letters used in mathematics, science, and engineering
*
* Vanna–Volga pricing
The Vanna–Volga method is a mathematical tool used in finance. It is a technique for pricing first-generation exotic options in foreign exchange market Foreign exchange derivative, (FX) derivatives.
Description
It consists of adjusting the Black ...
References
External links
Theory * Delta, Gamma, GammaP, Gamma symmetry, Vanna, Speed, Charm, Saddle GammaVanilla Options - Espen Haug
* Volga, Vanna, Speed, Charm, Color
Vanilla Options - Uwe Wystup
Step-by-step mathematical derivations of option Greeks
Derivation of European Vanilla Call Price
Derivation of European Vanilla Call Delta
Derivation of European Vanilla Call Gamma
Derivation of European Vanilla Call Speed
Derivation of European Vanilla Call Vega
Derivation of European Vanilla Call Volga
Derivation of European Vanilla Call Vanna as Derivative of Vega with respect to underlying
Derivation of European Vanilla Call Vanna as Derivative of Delta with respect to volatility
Derivation of European Vanilla Call Theta
Derivation of European Vanilla Call Rho
Derivation of European Vanilla Put Price
Derivation of European Vanilla Put Delta
Derivation of European Vanilla Put Gamma
Derivation of European Vanilla Put Speed
Derivation of European Vanilla Put Vega
Derivation of European Vanilla Put Volga
Derivation of European Vanilla Put Vanna as Derivative of Vega with respect to underlying
Derivation of European Vanilla Put Vanna as Derivative of Delta with respect to volatility
Derivation of European Vanilla Put Theta
Derivation of European Vanilla Put Rho
Online tools
Surface Plots of Black-Scholes Greeks
Chris Murray
Online real-time option prices and Greeks calculator when the underlying is normally distributed
Razvan Pascalau, Univ. of Alabama
R package to compute Greeks for European-, American- and Asian Options {{DEFAULTSORT:Greeks (Finance) Mathematical finance Financial ratios Options (finance)