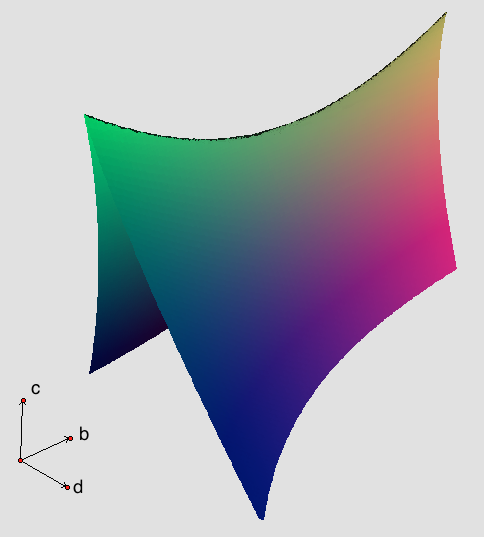
|
Delta (letter)
Delta (; uppercase Δ, lowercase δ or 𝛿; el, δέλτα, ''délta'', ) is the fourth letter of the Greek alphabet. In the system of Greek numerals it has a value of 4. It was derived from the Phoenician letter dalet 𐤃. Letters that come from delta include Latin D and Cyrillic Д. A river delta (originally, the delta of the Nile River) is so named because its shape approximates the triangular uppercase letter delta. Contrary to a popular legend, this use of the word ''delta'' was not coined by Herodotus. Pronunciation In Ancient Greek, delta represented a voiced dental plosive . In Modern Greek, it represents a voiced dental fricative , like the "th" in "that" or "this" (while in foreign words is instead commonly transcribed as ντ). Delta is romanized as ''d'' or ''dh''. Uppercase The uppercase letter Δ is used to denote: * Change of any changeable quantity, in mathematics and the sciences (more specifically, the difference operator); for example, in:\ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Greek Alphabet
The Greek alphabet has been used to write the Greek language since the late 9th or early 8th century BCE. It is derived from the earlier Phoenician alphabet, and was the earliest known alphabetic script to have distinct letters for vowels as well as consonants. In Archaic and early Classical times, the Greek alphabet existed in many local variants, but, by the end of the 4th century BCE, the Euclidean alphabet, with 24 letters, ordered from alpha to omega, had become standard and it is this version that is still used for Greek writing today. The uppercase and lowercase forms of the 24 letters are: : , , , , , , , , , , , , , , , , , /ς, , , , , , . The Greek alphabet is the ancestor of the Latin and Cyrillic scripts. Like Latin and Cyrillic, Greek originally had only a single form of each letter; it developed the letter case distinction between uppercase and lowercase in parallel with Latin during the modern era. Sound values and conventional transcriptions for some ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Latin
Latin (, or , ) is a classical language belonging to the Italic branch of the Indo-European languages. Latin was originally a dialect spoken in the lower Tiber area (then known as Latium) around present-day Rome, but through the power of the Roman Republic it became the dominant language in the Italian region and subsequently throughout the Roman Empire. Even after the fall of Western Rome, Latin remained the common language of international communication, science, scholarship and academia in Europe until well into the 18th century, when other regional vernaculars (including its own descendants, the Romance languages) supplanted it in common academic and political usage, and it eventually became a dead language in the modern linguistic definition. Latin is a highly inflected language, with three distinct genders (masculine, feminine, and neuter), six or seven noun cases (nominative, accusative, genitive, dative, ablative, and vocative), five declensions, four ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cramer's Rule
In linear algebra, Cramer's rule is an explicit formula for the solution of a system of linear equations with as many equations as unknowns, valid whenever the system has a unique solution. It expresses the solution in terms of the determinants of the (square) coefficient matrix and of matrices obtained from it by replacing one column by the column vector of right-sides of the equations. It is named after Gabriel Cramer (1704–1752), who published the rule for an arbitrary number of unknowns in 1750, although Colin Maclaurin also published special cases of the rule in 1748 (and possibly knew of it as early as 1729). Cramer's rule implemented in a naive way is computationally inefficient for systems of more than two or three equations. In the case of equations in unknowns, it requires computation of determinants, while Gaussian elimination produces the result with the same computational complexity as the computation of a single determinant. Cramer's rule can also be nu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Delta Baryon
The Delta baryons (or baryons, also called Delta resonances) are a family of subatomic particle made of three up or down quarks (u or d quarks), the same constituent quarks that make up the more familiar protons and neutrons. Properties Four closely related baryons exist: (constituent quarks: uuu), (uud), (udd), and (ddd), which respectively carry an electric charge of +2 , +1 , 0 , and −1 . The baryons have a mass of about ; their third component of isospin \; I_3 = \pm\tfrac ~\mathsf~ \pm\tfrac\;; and they are required to have an intrinsic spin of or higher (half-integer units). Ordinary nucleons (symbol , meaning either a proton or neutron), by contrast, have a mass of about , and both intrinsic spin and isospin of . The (uud) and (udd) particles are higher-mass spin-excitations of the proton (, uud) and neutron (, udd), respectively. The and , however, have no direct nucleon analogues: ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Uncertainty Principle
In quantum mechanics, the uncertainty principle (also known as Heisenberg's uncertainty principle) is any of a variety of mathematical inequalities asserting a fundamental limit to the accuracy with which the values for certain pairs of physical quantities of a particle, such as position, ''x'', and momentum, ''p'', can be predicted from initial conditions. Such variable pairs are known as complementary variables or canonically conjugate variables; and, depending on interpretation, the uncertainty principle limits to what extent such conjugate properties maintain their approximate meaning, as the mathematical framework of quantum physics does not support the notion of simultaneously well-defined conjugate properties expressed by a single value. The uncertainty principle implies that it is in general not possible to predict the value of a quantity with arbitrary certainty, even if all initial conditions are specified. Introduced first in 1927 by the German physicist Wern ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Uncertainty
Uncertainty refers to Epistemology, epistemic situations involving imperfect or unknown information. It applies to predictions of future events, to physical measurements that are already made, or to the unknown. Uncertainty arises in partially observable or stochastic environments, as well as due to ignorance, Laziness, indolence, or both. It arises in any number of fields, including insurance, philosophy, physics, statistics, economics, finance, medicine, psychology, sociology, engineering, metrology, meteorology, ecology and information science. Concepts Although the terms are used in various ways among the general public, many specialists in decision theory, statistics and other quantitative fields have defined uncertainty, risk, and their measurement as: Uncertainty The lack of certainty, a state of limited knowledge where it is impossible to exactly describe the existing state, a future outcome, or more than one possible outcome. ;Measurement of uncertainty: A set of po ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Symmetric Difference
In mathematics, the symmetric difference of two sets, also known as the disjunctive union, is the set of elements which are in either of the sets, but not in their intersection. For example, the symmetric difference of the sets \ and \ is \. The symmetric difference of the sets ''A'' and ''B'' is commonly denoted by A \ominus B, or A\operatorname \triangle B. The power set of any set becomes an abelian group under the operation of symmetric difference, with the empty set as the neutral element of the group and every element in this group being its own inverse. The power set of any set becomes a Boolean ring, with symmetric difference as the addition of the ring and intersection as the multiplication of the ring. Properties The symmetric difference is equivalent to the union of both relative complements, that is: :A\,\triangle\,B = \left(A \setminus B\right) \cup \left(B \setminus A\right), The symmetric difference can also be expressed using the XOR operation ⊕ o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Area Of A Triangle
A triangle is a polygon with three edges and three vertices. It is one of the basic shapes in geometry. A triangle with vertices ''A'', ''B'', and ''C'' is denoted \triangle ABC. In Euclidean geometry, any three points, when non-collinear, determine a unique triangle and simultaneously, a unique plane (i.e. a two-dimensional Euclidean space). In other words, there is only one plane that contains that triangle, and every triangle is contained in some plane. If the entire geometry is only the Euclidean plane, there is only one plane and all triangles are contained in it; however, in higher-dimensional Euclidean spaces, this is no longer true. This article is about triangles in Euclidean geometry, and in particular, the Euclidean plane, except where otherwise noted. Types of triangle The terminology for categorizing triangles is more than two thousand years old, having been defined on the very first page of Euclid's Elements. The names used for modern classification are eith ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quadratic Equation
In algebra, a quadratic equation () is any equation that can be rearranged in standard form as ax^2 + bx + c = 0\,, where represents an unknown (mathematics), unknown value, and , , and represent known numbers, where . (If and then the equation is linear equation, linear, not quadratic.) The numbers , , and are the ''coefficients'' of the equation and may be distinguished by respectively calling them, the ''quadratic coefficient'', the ''linear coefficient'' and the ''constant'' or ''free term''. The values of that satisfy the equation are called ''solution (mathematics), solutions'' of the equation, and ''zero of a function, roots'' or ''zero of a function, zeros'' of the Expression (mathematics), expression on its left-hand side. A quadratic equation has at most two solutions. If there is only one solution, one says that it is a double root. If all the coefficients are real numbers, there are either two real solutions, or a single real double root, or two complex number, c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polynomial
In mathematics, a polynomial is an expression consisting of indeterminates (also called variables) and coefficients, that involves only the operations of addition, subtraction, multiplication, and positive-integer powers of variables. An example of a polynomial of a single indeterminate is . An example with three indeterminates is . Polynomials appear in many areas of mathematics and science. For example, they are used to form polynomial equations, which encode a wide range of problems, from elementary word problems to complicated scientific problems; they are used to define polynomial functions, which appear in settings ranging from basic chemistry and physics to economics and social science; they are used in calculus and numerical analysis to approximate other functions. In advanced mathematics, polynomials are used to construct polynomial rings and algebraic varieties, which are central concepts in algebra and algebraic geometry. Etymology The word ''polynomial'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discriminant
In mathematics, the discriminant of a polynomial is a quantity that depends on the coefficients and allows deducing some properties of the roots without computing them. More precisely, it is a polynomial function of the coefficients of the original polynomial. The discriminant is widely used in polynomial factoring, number theory, and algebraic geometry. The discriminant of the quadratic polynomial ax^2+bx+c is :b^2-4ac, the quantity which appears under the square root in the quadratic formula. If a\ne 0, this discriminant is zero if and only if the polynomial has a double root. In the case of real coefficients, it is positive if the polynomial has two distinct real roots, and negative if it has two distinct complex conjugate roots. Similarly, the discriminant of a cubic polynomial is zero if and only if the polynomial has a multiple root. In the case of a cubic with real coefficients, the discriminant is positive if the polynomial has three distinct real roots, and negati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Laplace Operator
In mathematics, the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a scalar function on Euclidean space. It is usually denoted by the symbols \nabla\cdot\nabla, \nabla^2 (where \nabla is the nabla operator), or \Delta. In a Cartesian coordinate system, the Laplacian is given by the sum of second partial derivatives of the function with respect to each independent variable. In other coordinate systems, such as cylindrical and spherical coordinates, the Laplacian also has a useful form. Informally, the Laplacian of a function at a point measures by how much the average value of over small spheres or balls centered at deviates from . The Laplace operator is named after the French mathematician Pierre-Simon de Laplace (1749–1827), who first applied the operator to the study of celestial mechanics: the Laplacian of the gravitational potential due to a given mass density distribution is a constant multiple of that d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |