Rotation Matrix

In linear algebra, a rotation matrix is a transformation matrix that is used to perform a rotation in Euclidean space. For example, using the convention below, the matrix

:$R = \begin \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end$

rotates points in the plane counterclockwise through an angle about the origin of a two-dimensional Cartesian coordinate system. To perform the rotation on a plane point with standard coordinates , it should be written as a column vector, and multiplied by the matrix :

:$R\mathbf = \begin \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end \begin x \\ y \end = \begin x\cos\theta-y\sin\theta \\ x\sin\theta+y\cos\theta \end.$

If and are the coordinates of the endpoint of a vector with the length ''r'' and the angle $\phi$ with respect to the -axis, so that $x = r \cos \phi$ and $y = r \sin \phi$, then the above equations become the trigonometric summation angle formulae:$R\mathbf = r\begin \cos\phi\cos\theta-\sin\phi\sin\theta \\ \cos\phi\sin\theta+\sin\phi\cos\theta \end = r\begin \cos(\phi+\theta)\\ \sin(\phi+\theta) \end.$Indeed, this is the trigonometric summation angle formulae in matrix form. One way to understand this is to say we have a vector at an angle 30° from the -axis, and we wish to rotate that angle by a further 45°. We simply need to compute the vector endpoint coordinates at 75°.

The examples in this article apply to '' active rotations'' of vectors ''counterclockwise'' in a ''right-handed coordinate system'' ( counterclockwise from ) by ''pre-multiplication'' (the rotation matrix applied on the left of the column vector to be rotated). If any one of these is changed (such as rotating axes instead of vectors, a '' passive transformation''), then the inverse of the example matrix should be used, which coincides with its transpose.

Since matrix multiplication has no effect on the zero vector (the coordinates of the origin), rotation matrices describe rotations about the origin. Rotation matrices provide an algebraic description of such rotations, and are used extensively for computations in geometry, physics, and computer graphics. In some literature, the term ''rotation'' is generalized to include improper rotations, characterized by orthogonal matrices with a determinant of −1 (instead of +1). An improper rotation combines a ''proper'' rotation with ''reflections'' (which invert orientation). In other cases, where reflections are not being considered, the label ''proper'' may be dropped. The latter convention is followed in this article.

Rotation matrices are square matrices, with real entries. More specifically, they can be characterized as orthogonal matrices with determinant 1; that is, a square matrix is a rotation matrix if and only if and . The set of all orthogonal matrices of size with determinant +1 is a representation of a group known as the special orthogonal group , one example of which is the rotation group SO(3). The set of all orthogonal matrices of size with determinant +1 or −1 is a representation of the (general) orthogonal group .

In two dimensions

In two dimensions, the standard rotation matrix has the following form:
:$R(\theta) = \begin \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \\ \end.$

This rotates column vectors by means of the following matrix multiplication,
:$\begin x' \\ y' \\ \end = \begin \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \\ \end\begin x \\ y \\ \end.$

Thus, the new coordinates of a point after rotation are
:$\begin x' &= x \cos\theta - y \sin\theta\, \\ y' &= x \sin\theta + y \cos\theta\, \end.$

Examples

For example, when the vector (initially aligned with the ''x''-axis of the Cartesian coordinate system)
:$\mathbf = \begin 1 \\ 0 \\ \end$
is rotated by an angle , its new coordinates are
:$\begin \cos\theta \\ \sin\theta \\ \end,$

and when the vector (initially aligned with the ''y''-axis of the coordinate system)
:$\mathbf = \begin 0 \\ 1 \\ \end$
is rotated by an angle , its new coordinates are
:$\begin -\sin\theta \\ \cos\theta \\ \end.$

Direction

The direction of vector rotation is counterclockwise if is positive (e.g. 90°), and clockwise if is negative (e.g. −90°) for $R(\theta)$. Thus the clockwise rotation matrix is found as (by replacing with and using the trigonometric symmetry of $\sin(-\theta) = - \sin(\theta)$ and $\cos( - \theta) = \cos(\theta)$)
:$R(-\theta) = \begin \cos\theta & \sin\theta \\ -\sin\theta & \cos\theta \\ \end.$

An alternative convention uses rotating axes (instead of rotating a vector), and the above matrices also represent a rotation of the ''axes clockwise'' through an angle .

The two-dimensional case is the only non-trivial case where the rotation matrices group is commutative; it does not matter in which order rotations are multiply performed. For the 3-dimensional case, for example, a different order of multiple rotations gives a different result. (E.g., rotating a cell phone along ''z''-axis then ''y''-axis is not equal to rotations along the ''y''-axis then ''z''-axis.)

Non-standard orientation of the coordinate system

If a standard right-handed Cartesian coordinate system is used, with the to the right and the up, the rotation is counterclockwise. If a left-handed Cartesian coordinate system is used, with directed to the right but directed down, is clockwise. Such non-standard orientations are rarely used in mathematics but are common in 2D computer graphics, which often have the origin in the top left corner and the down the screen or page.

See below for other alternative conventions which may change the sense of the rotation produced by a rotation matrix.

Common 2D rotations

Matrices
:\begin
0 & -1 \\ pt 1 & 0 \\
\end, \quad
\begin
-1 & 0 \\ pt 0 & -1 \\
\end, \quad
\begin
0 & 1 \\ pt -1 & 0 \\
\end
are 2D rotation matrices corresponding to counter-clockwise rotations of respective angles of 90°, 180°, and 270°.

Relationship with complex plane

The matrices of the shape
$\begin x & -y \\ y & x \end$ form a ring, since their set is closed under addition and multiplication.
Since
$\begin 0 & -1 \\ 1 & 0 \end^2 \ =\ \begin -1 & 0 \\ 0 & -1 \end \ = -I$
(where $I$ is the identity matrix), the map
:$\begin x & -y \\ y & x \end = x\begin 1 & 0 \\ 0 & 1 \end + y \begin 0 & -1 \\ 1 & 0 \end \mapsto x+iy$
(where $i = \begin 0 & -1 \\ 1 & 0 \end$) is a ring isomorphism from this ring to the field of the complex numbers (incidentally, this shows that this ring is a field). Under this isomorphism, the rotation matrices correspond to the circle of the unit complex numbers, the complex numbers of modulus .

If one identifies $\mathbb R^2$ with $\mathbb C$ through the linear isomorphism $(a,b)\mapsto a+ib$, where $(a,b) \in \mathbb R^2$ and $a+ib \in \mathbb C$, the action of a matrix $\begin x & -y \\ y & x \end$ on a vector $(a,b)$ corresponds to multiplication on the complex number $a+ib$ by , and a rotation correspond to multiplication by a complex number of modulus .

As every 2-dimensional rotation matrix can be written
:$\begin\cos t&-\sin t\\ \sin t&\cos t\end,$
the above correspondence associates such a matrix with the complex number
:$e^ = \cos t + i\sin t = \cos t \begin 1 & 0 \\ 0 & 1 \end + \sin t \begin 0 & -1 \\ 1 & 0 \end$
where the first equality is Euler's formula, the matrix $I = \begin 1 & 0 \\ 0 & 1 \end$corresponds to 1, and the matrix $\begin 0 & -1 \\ 1 & 0 \end$ corresponds to the imaginary unit $i$.

In three dimensions

Basic 3D rotations

A basic 3D rotation (also called elemental rotation) is a rotation about one of the axes of a coordinate system. The following three basic rotation matrices rotate vectors by an angle about the -, -, or -axis, in three dimensions, using the right-hand rule—which codifies their alternating signs. Notice that the right-hand rule only works when multiplying $R \cdot \vec$. (The same matrices can also represent a clockwise rotation of the axes.Note that if instead of rotating vectors, it is the reference frame that is being rotated, the signs on the terms will be reversed. If reference frame A is rotated anti-clockwise about the origin through an angle to create reference frame B, then (with the signs flipped) will transform a vector described in reference frame A coordinates to reference frame B coordinates. Coordinate frame transformations in aerospace, robotics, and other fields are often performed using this interpretation of the rotation matrix.)

:
\begin
R_x(\theta) &= \begin
1 & 0 & 0 \\
0 & \cos \theta & -\sin \theta \\ pt0 & \sin \theta & \cos \theta \\ pt\end \\ ptR_y(\theta) &= \begin
\cos \theta & 0 & \sin \theta \\ pt0 & 1 & 0 \\ pt-\sin \theta & 0 & \cos \theta \\
\end \\ ptR_z(\theta) &= \begin
\cos \theta & -\sin \theta & 0 \\ pt\sin \theta & \cos \theta & 0 \\ pt0 & 0 & 1 \\
\end
\end

For column vectors, each of these basic vector rotations appears counterclockwise when the axis about which they occur points toward the observer, the coordinate system is right-handed, and the angle is positive. , for instance, would rotate toward the a vector aligned with the , as can easily be checked by operating with on the vector :
:$R_z(90^\circ) \begin 1 \\ 0 \\ 0 \\ \end = \begin \cos 90^\circ & -\sin 90^\circ & 0 \\ \sin 90^\circ & \quad\cos 90^\circ & 0\\ 0 & 0 & 1\\ \end \begin 1 \\ 0 \\ 0 \\ \end = \begin 0 & -1 & 0 \\ 1 & 0 & 0\\ 0 & 0 & 1\\ \end \begin 1 \\ 0 \\ 0 \\ \end = \begin 0 \\ 1 \\ 0 \\ \end$

This is similar to the rotation produced by the above-mentioned two-dimensional rotation matrix. See below for alternative conventions which may apparently or actually invert the sense of the rotation produced by these matrices.

General 3D rotations

Other 3D rotation matrices can be obtained from these three using matrix multiplication. For example, the product
:$\begin R = R_z(\alpha) \, R_y(\beta) \, R_x(\gamma) &= \overset\text \overset\text \overset\text \\ &= \begin \cos\alpha\cos\beta & \cos\alpha\sin\beta\sin\gamma - \sin\alpha\cos\gamma & \cos\alpha\sin\beta\cos\gamma + \sin\alpha\sin\gamma \\ \sin\alpha\cos\beta & \sin\alpha\sin\beta\sin\gamma + \cos\alpha\cos\gamma & \sin\alpha\sin\beta\cos\gamma - \cos\alpha\sin\gamma \\ -\sin\beta & \cos\beta\sin\gamma & \cos\beta\cos\gamma \\ \end \end$

represents a rotation whose yaw, pitch, and roll angles are , and , respectively. More formally, it is an intrinsic rotation whose Tait–Bryan angles are , , , about axes , , , respectively.
Similarly, the product
:$\begin \\ R = R_x(\gamma) \, R_y(\beta) \, R_z(\alpha) &= \overset\text \overset\text \overset\text \\ &= \begin \cos\beta\cos\gamma & \sin\alpha\sin\beta\cos\gamma - \cos\alpha\sin\gamma & \cos\alpha\sin\beta\cos\gamma + \sin\alpha\sin\gamma \\ \cos\beta\sin\gamma & \sin\alpha\sin\beta\sin\gamma + \cos\alpha\cos\gamma & \cos\alpha\sin\beta\sin\gamma - \sin\alpha\cos\gamma \\ -\sin\beta & \sin\alpha\cos\beta & \cos\alpha\cos\beta \\ \end \end$
represents an extrinsic rotation whose (improper) Euler angles are , , , about axes , , .

These matrices produce the desired effect only if they are used to premultiply column vectors, and (since in general matrix multiplication is not commutative) only if they are applied in the specified order (see Ambiguities for more details). The order of rotation operations is from right to left; the matrix adjacent to the column vector is the first to be applied, and then the one to the left.

Conversion from rotation matrix to axis–angle

Every rotation in three dimensions is defined by its axis (a vector along this axis is unchanged by the rotation), and its angle — the amount of rotation about that axis ( Euler rotation theorem).

There are several methods to compute the axis and angle from a rotation matrix (see also axis–angle representation). Here, we only describe the method based on the computation of the eigenvectors and eigenvalues of the rotation matrix. It is also possible to use the trace of the rotation matrix.

Determining the axis

Given a rotation matrix , a vector parallel to the rotation axis must satisfy
:$R\mathbf = \mathbf,$
since the rotation of around the rotation axis must result in . The equation above may be solved for which is unique up to a scalar factor unless is the identity matrix .

Further, the equation may be rewritten
:$R\mathbf = I \mathbf \implies \left(R - I\right) \mathbf = 0,$
which shows that lies in the null space of .

Viewed in another way, is an eigenvector of corresponding to the eigenvalue . Every rotation matrix must have this eigenvalue, the other two eigenvalues being complex conjugates of each other. It follows that a general rotation matrix in three dimensions has, up to a multiplicative constant, only one real eigenvector.

One way to determine the rotation axis is by showing that:

:$\begin 0 &= R^\mathsf 0 + 0 \\ &= R^\mathsf\left(R - I\right) \mathbf + \left(R - I\right) \mathbf \\ &= \left(R^\mathsfR - R^\mathsf + R - I\right) \mathbf \\ &= \left(I - R^\mathsf + R - I\right) \mathbf \\ &= \left(R - R^\mathsf\right) \mathbf \end$

Since is a skew-symmetric matrix, we can choose such that
: mathbf u = \left(R - R^\mathsf\right).
The matrix–vector product becomes a cross product of a vector with itself, ensuring that the result is zero:

:\left(R - R^\mathsf\right) \mathbf = mathbf u \mathbf = \mathbf \times \mathbf = 0\,

Therefore, if
:$R = \begin a & b & c \\ d & e & f \\ g & h & i \\ \end,$
then
:$\mathbf = \begin h-f \\ c-g \\ d-b \\ \end.$
The magnitude of computed this way is , where is the angle of rotation.

This does not work if is symmetric. Above, if is zero, then all subsequent steps are invalid. In this case, the angle of rotation is 0° or 180° and any nonzero column of is an eigenvector of with eigenvalue 1 because .

Determining the angle

To find the angle of a rotation, once the axis of the rotation is known, select a vector perpendicular to the axis. Then the angle of the rotation is the angle between and .

A more direct method, however, is to simply calculate the trace: the sum of the diagonal elements of the rotation matrix. Care should be taken to select the right sign for the angle to match the chosen axis:
:$\operatorname (R) = 1 + 2\cos\theta ,$

from which follows that the angle's absolute value is
:$, \theta, = \arccos\left(\frac\right).$

For the rotation axis $\mathbf=(n_1,n_2,n_3)$, you can get the correct angle from

$\left\{\begin{matrix} \cos \theta&=&\dfrac{\operatorname{tr}(R) - 1}{2}\\ \sin \theta&=&-\dfrac{\operatorname{tr}(K_n R)}{2} \end{matrix}\right.$

where

$K_n=\begin{bmatrix} 0 & -n_3 & n_2\\ n_3 & 0 & -n_1\\ -n_2 & n_1 & 0\\ \end{bmatrix}$

Rotation matrix from axis and angle

The matrix of a proper rotation by angle around the axis , a unit vector with , is given by:

:$R = \begin{bmatrix} u_x^2 \left(1-\cos \theta\right) + \cos \theta & u_x u_y \left(1-\cos \theta\right) - u_z \sin \theta & u_x u_z \left(1-\cos \theta\right) + u_y \sin \theta \\ u_x u_y \left(1-\cos \theta\right) + u_z \sin \theta & u_y^2\left(1-\cos \theta\right) + \cos \theta & u_y u_z \left(1-\cos \theta\right) - u_x \sin \theta \\ u_x u_z \left(1-\cos \theta\right) - u_y \sin \theta & u_y u_z \left(1-\cos \theta\right) + u_x \sin \theta & u_z^2\left(1-\cos \theta\right) + \cos \theta \end{bmatrix}.$

A derivation of this matrix from first principles can be found in section 9.2 here. The basic idea to derive this matrix is dividing the problem into few known simple steps.

# First rotate the given axis and the point such that the axis lies in one of the coordinate planes (, or )
# Then rotate the given axis and the point such that the axis is aligned with one of the two coordinate axes for that particular coordinate plane (, or )
# Use one of the fundamental rotation matrices to rotate the point depending on the coordinate axis with which the rotation axis is aligned.
# Reverse rotate the axis-point pair such that it attains the final configuration as that was in step 2 (Undoing step 2)
# Reverse rotate the axis-point pair which was done in step 1 (undoing step 1)

This can be written more concisely as

:R = (\cos\theta)\,I + (\sin\theta)\, mathbf u{\times} + (1-\cos\theta)\,(\mathbf{u}\otimes\mathbf{u}),
where is the cross product matrix of ; the expression is the outer product, and is the identity matrix. Alternatively, the matrix entries are:
:$R_{jk}=\begin{cases} \cos^2\frac{\theta}{2}+\sin^2\frac{\theta}{2}\left(2u_j^2-1\right), \quad &\text{if }j=k\\ 2u_ju_k\sin^2\frac{\theta}{2}-\varepsilon_{jkl}u_l\sin\theta, \quad &\text{if }j\neq k \end{cases}$

where is the Levi-Civita symbol with . This is a matrix form of Rodrigues' rotation formula, (or the equivalent, differently parametrized Euler–Rodrigues formula) withNote that

: \mathbf{u}\otimes\mathbf{u} = \bigl( mathbf u{\times}\bigr)^2+{\mathbf I}
so that, in Rodrigues' notation, equivalently,

: \mathbf{R} = \mathbf{I} + (\sin\theta) mathbf u{\times} + (1-\cos\theta)\bigl( mathbf u{\times}\bigr)^2.

: \mathbf{u}\otimes\mathbf{u} = \mathbf{u}\mathbf{u}^\mathsf{T} = \begin{bmatrix}
u_x^2 & u_x u_y & u_x u_z \\ ptu_x u_y & u_y^2 & u_y u_z \\ ptu_x u_z & u_y u_z & u_z^2
\end{bmatrix},\qquad mathbf u{\times} = \begin{bmatrix}
0 & -u_z & u_y \\ ptu_z & 0 & -u_x \\ pt-u_y & u_x & 0
\end{bmatrix}.

In $\mathbb{R}^3$ the rotation of a vector around the axis by an angle can be written as:
:$R_{\mathbf{u(\theta)\mathbf{x}=\mathbf{u}(\mathbf{u}\cdot\mathbf{x})+\cos\left(\theta\right)(\mathbf{u}\times\mathbf{x})\times\mathbf{u}+\sin\left(\theta\right)(\mathbf{u}\times\mathbf{x})$

or equivalently:
:$R_{\mathbf{u(\theta)\mathbf{x}= \mathbf{x} \cos(\theta) + \mathbf{u}(\mathbf{x} \cdot \mathbf{u})(1- \cos(\theta)) - \mathbf{x} \times \mathbf{u} \sin{\theta}$

This can also be written in tensor notation as:
:$(R_{\mathbf{u(\theta)\mathbf{x})_i = (R_{\mathbf{u(\theta))_{ij} {\mathbf{x_{j} \quad \text{with} \quad (R_{\mathbf{u(\theta))_{ij} = \delta_{ij}\cos(\theta) + \mathbf{u}_i\mathbf{u}_j (1- \cos(\theta)) - \sin{\theta} \varepsilon_{ijk} \mathbf{u}_{k}$

If the 3D space is right-handed and , this rotation will be counterclockwise when points towards the observer ( Right-hand rule). Explicitly, with $(\boldsymbol{\alpha}, \boldsymbol{\beta},\mathbf u)$ a right-handed orthonormal basis,
:$R_{\mathbf{u(\theta)\boldsymbol{\alpha}= \cos\left(\theta\right) \boldsymbol{\alpha} + \sin\left(\theta\right) \boldsymbol{\beta}, \quad R_{\mathbf{u(\theta)\boldsymbol{\beta}= - \sin\left(\theta\right) \boldsymbol{\alpha} + \cos\left(\theta\right) \boldsymbol{\beta}, \quad R_{\mathbf{u(\theta)\mathbf{u}=\mathbf{u}.$

Note the striking ''merely apparent differences'' to the ''equivalent'' Lie-algebraic formulation below.

Properties

For any -dimensional rotation matrix acting on $\mathbb{R}^n,$
: $R^\mathsf{T} = R^{-1}$ (The rotation is an orthogonal matrix)
It follows that:
: $\det R = \pm 1$

A rotation is termed proper if , and improper (or a roto-reflection) if . For even dimensions , the eigenvalues of a proper rotation occur as pairs of complex conjugates which are roots of unity: for , which is real only for . Therefore, there may be no vectors fixed by the rotation (), and thus no axis of rotation. Any fixed eigenvectors occur in pairs, and the axis of rotation is an even-dimensional subspace.

For odd dimensions , a proper rotation will have an odd number of eigenvalues, with at least one and the axis of rotation will be an odd dimensional subspace. Proof:
:$\begin{align} \det\left(R - I\right) &= \det\left(R^\mathsf{T}\right) \det\left(R - I\right) = \det\left(R^\mathsf{T}R - R^\mathsf{T}\right) = \det\left(I - R^\mathsf{T}\right) \\ &= \det(I - R) = \left(-1\right)^n \det\left(R - I\right) = -\det\left(R - I\right). \end{align}$

Here is the identity matrix, and we use , as well as since is odd. Therefore, , meaning there is a nonzero vector with , that is , a fixed eigenvector. There may also be pairs of fixed eigenvectors in the even-dimensional subspace orthogonal to , so the total dimension of fixed eigenvectors is odd.

For example, in 2-space , a rotation by angle has eigenvalues and , so there is no axis of rotation except when , the case of the null rotation. In 3-space , the axis of a non-null proper rotation is always a unique line, and a rotation around this axis by angle has eigenvalues . In 4-space , the four eigenvalues are of the form . The null rotation has . The case of is called a ''simple rotation'', with two unit eigenvalues forming an ''axis plane'', and a two-dimensional rotation orthogonal to the axis plane. Otherwise, there is no axis plane. The case of is called an ''isoclinic rotation'', having eigenvalues repeated twice, so every vector is rotated through an angle .

The trace of a rotation matrix is equal to the sum of its eigenvalues. For , a rotation by angle has trace . For , a rotation around any axis by angle has trace . For , and the trace is , which becomes for an isoclinic rotation.

Examples

*The rotation matrix
::$Q = \begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix}$
:corresponds to a 90° planar rotation clockwise about the origin.

*The transpose of the matrix
::$M = \begin{bmatrix} 0.936 & 0.352 \\ 0.352 & -0.936 \end{bmatrix}$
:is its inverse, but since its determinant is −1, this is not a proper rotation matrix; it is a reflection across the line .

*The rotation matrix
::$Q = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \frac{\sqrt{3{2} & \frac12 \\ 0 & -\frac12 & \frac{\sqrt{3{2} \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos 30^\circ & \sin 30^\circ \\ 0 & -\sin 30^\circ & \cos 30^\circ \\ \end{bmatrix}$
:corresponds to a −30° rotation around the -axis in three-dimensional space.

*The rotation matrix
::$Q = \begin{bmatrix} 0.36 & 0.48 & -0.80 \\ -0.80 & 0.60 & 0.00 \\ 0.48 & 0.64 & 0.60 \end{bmatrix}$
:corresponds to a rotation of approximately −74° around the axis in three-dimensional space.

*The permutation matrix
::$P = \begin{bmatrix} 0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{bmatrix}$
:is a rotation matrix, as is the matrix of any even permutation, and rotates through 120° about the axis .

*The matrix
::$M = \begin{bmatrix} 3 & -4 & 1 \\ 5 & 3 & -7 \\ -9 & 2 & 6 \end{bmatrix}$
:has determinant +1, but is not orthogonal (its transpose is not its inverse), so it is not a rotation matrix.

*The matrix
::$M = \begin{bmatrix} 0.5 & -0.1 & 0.7 \\ 0.1 & 0.5 & -0.5 \\ -0.7 & 0.5 & 0.5 \\ -0.5 & -0.7 & -0.1 \end{bmatrix}$
:is not square, and so cannot be a rotation matrix; yet yields a identity matrix (the columns are orthonormal).

*The matrix
::$Q = -I = \begin{bmatrix} -1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & -1 \end{bmatrix}$
:describes an isoclinic rotation in four dimensions, a rotation through equal angles (180°) through two orthogonal planes.

*The rotation matrix
::$Q = \begin{bmatrix} 0 & -1 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & -1 & 0 & 0 \\ 0 & 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & 0 & 1 \end{bmatrix}$
:rotates vectors in the plane of the first two coordinate axes 90°, rotates vectors in the plane of the next two axes 180°, and leaves the last coordinate axis unmoved.

Geometry

In Euclidean geometry, a rotation is an example of an isometry, a transformation that moves points without changing the distances between them. Rotations are distinguished from other isometries by two additional properties: they leave (at least) one point fixed, and they leave "handedness" unchanged. In contrast, a translation moves every point, a reflection exchanges left- and right-handed ordering, a glide reflection does both, and an improper rotation combines a change in handedness with a normal rotation.

If a fixed point is taken as the origin of a Cartesian coordinate system, then every point can be given coordinates as a displacement from the origin. Thus one may work with the vector space of displacements instead of the points themselves. Now suppose are the coordinates of the vector from the origin to point . Choose an orthonormal basis for our coordinates; then the squared distance to , by Pythagoras, is
:$d^2(O,P) = \, \mathbf{p} \, ^2 = \sum_{r=1}^n p_r^2$
which can be computed using the matrix multiplication
:$\, \mathbf{p} \, ^2 = \begin{bmatrix}p_1 \cdots p_n\end{bmatrix} \begin{bmatrix}p_1 \\ \vdots \\ p_n \end{bmatrix} = \mathbf{p}^\mathsf{T} \mathbf{p} .$

A geometric rotation transforms lines to lines, and preserves ratios of distances between points. From these properties it can be shown that a rotation is a linear transformation of the vectors, and thus can be written in matrix form, . The fact that a rotation preserves, not just ratios, but distances themselves, is stated as
:$\mathbf{p}^\mathsf{T} \mathbf{p} = (Q \mathbf{p})^\mathsf{T} (Q \mathbf{p}) ,$
or
:$\begin{align} \mathbf{p}^\mathsf{T} I \mathbf{p}&{}= \left(\mathbf{p}^\mathsf{T} Q^\mathsf{T}\right) (Q \mathbf{p}) \\ &{}= \mathbf{p}^\mathsf{T} \left(Q^\mathsf{T} Q\right) \mathbf{p} . \end{align}$
Because this equation holds for all vectors, , one concludes that every rotation matrix, , satisfies the orthogonality condition,
:$Q^\mathsf{T} Q = I .$
Rotations preserve handedness because they cannot change the ordering of the axes, which implies the special matrix condition,
:$\det Q = +1 .$
Equally important, it can be shown that any matrix satisfying these two conditions acts as a rotation.

Multiplication

The inverse of a rotation matrix is its transpose, which is also a rotation matrix:
:$\begin{align} \left(Q^\mathsf{T}\right)^\mathsf{T} \left(Q^\mathsf{T}\right) &= Q Q^\mathsf{T} = I\\ \det Q^\mathsf{T} &= \det Q = +1. \end{align}$
The product of two rotation matrices is a rotation matrix:
:$\begin{align} \left(Q_1 Q_2\right)^\mathsf{T} \left(Q_1 Q_2\right) &= Q_2^\mathsf{T} \left(Q_1^\mathsf{T} Q_1\right) Q_2 = I \\ \det \left(Q_1 Q_2\right) &= \left(\det Q_1\right) \left(\det Q_2\right) = +1. \end{align}$
For , multiplication of rotation matrices is generally not commutative.
:$\begin{align} Q_1 &= \begin{bmatrix}0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1\end{bmatrix} & Q_2 &= \begin{bmatrix}0 & 0 & 1 \\ 0 & 1 & 0 \\ -1 & 0 & 0\end{bmatrix} \\ Q_1 Q_2 &= \begin{bmatrix}0 & -1 & 0 \\ 0 & 0 & 1 \\ -1 & 0 & 0\end{bmatrix} & Q_2 Q_1 &= \begin{bmatrix}0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0\end{bmatrix}. \end{align}$
Noting that any identity matrix is a rotation matrix, and that matrix multiplication is associative, we may summarize all these properties by saying that the rotation matrices form a group, which for is non-abelian, called a special orthogonal group, and denoted by , , , or , the group of rotation matrices is isomorphic to the group of rotations in an space. This means that multiplication of rotation matrices corresponds to composition of rotations, applied in left-to-right order of their corresponding matrices.

Ambiguities

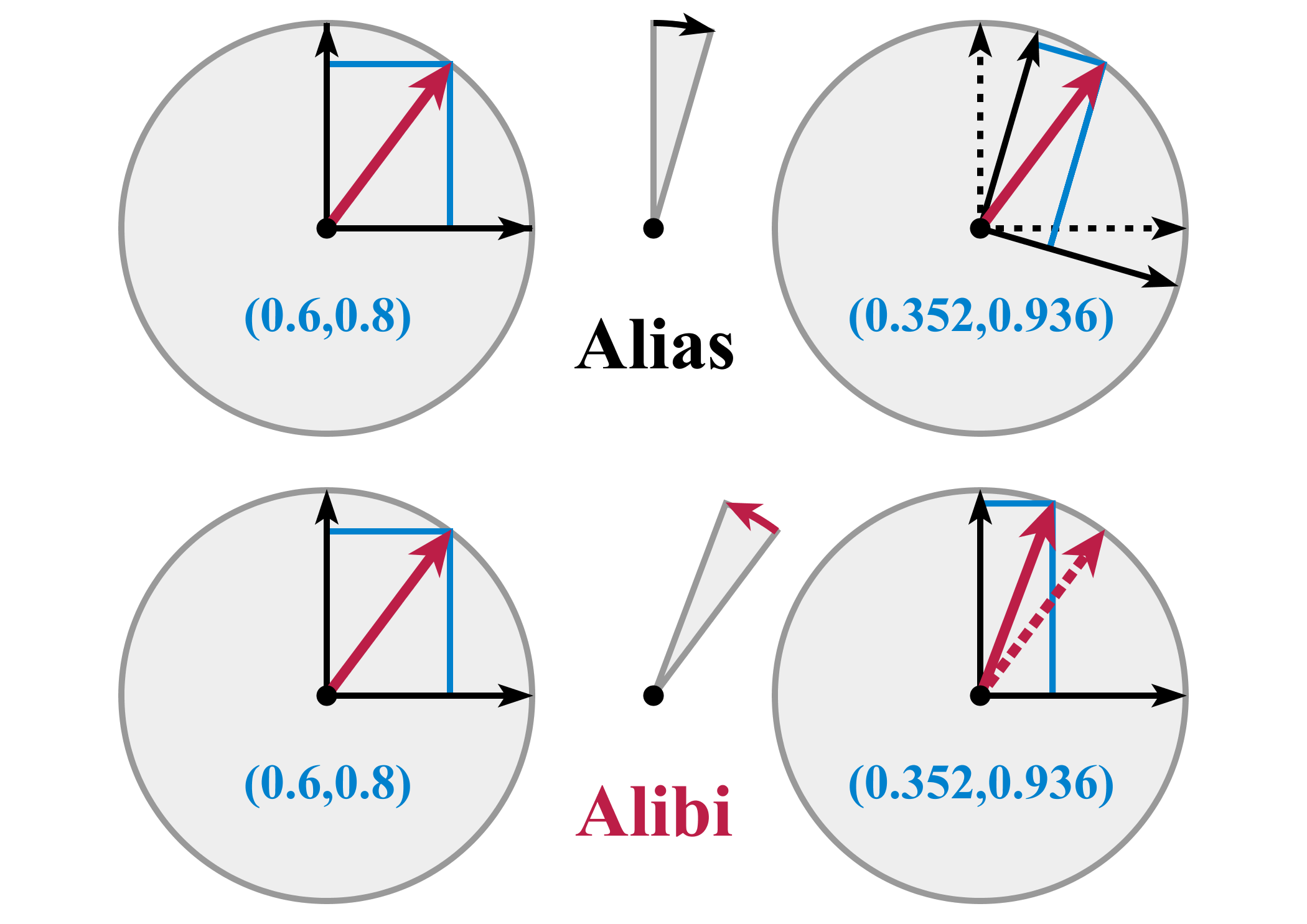
The interpretation of a rotation matrix can be subject to many ambiguities.

In most cases the effect of the ambiguity is equivalent to the effect of a rotation matrix inversion (for these orthogonal matrices equivalently matrix transpose).

; Alias or alibi (passive or active) transformation
: The coordinates of a point may change due to either a rotation of the coordinate system ( alias), or a rotation of the point ( alibi). In the latter case, the rotation of also produces a rotation of the vector representing . In other words, either and are fixed while rotates (alias), or is fixed while and rotate (alibi). Any given rotation can be legitimately described both ways, as vectors and coordinate systems actually rotate with respect to each other, about the same axis but in opposite directions. Throughout this article, we chose the alibi approach to describe rotations. For instance,
::$R(\theta) = \begin{bmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \\ \end{bmatrix}$
: represents a counterclockwise rotation of a vector by an angle , or a rotation of by the same angle but in the opposite direction (i.e. clockwise). Alibi and alias transformations are also known as active and passive transformations, respectively.
; Pre-multiplication or post-multiplication
: The same point can be represented either by a column vector or a row vector . Rotation matrices can either pre-multiply column vectors (), or post-multiply row vectors (). However, produces a rotation in the opposite direction with respect to . Throughout this article, rotations produced on column vectors are described by means of a pre-multiplication. To obtain exactly the same rotation (i.e. the same final coordinates of point ), the equivalent row vector must be post-multiplied by the transpose of (i.e. ).
; Right- or left-handed coordinates
: The matrix and the vector can be represented with respect to a right-handed or left-handed coordinate system. Throughout the article, we assumed a right-handed orientation, unless otherwise specified.
; Vectors or forms
: The vector space has a dual space of linear forms, and the matrix can act on either vectors or forms.

Decompositions

Independent planes

Consider the rotation matrix
:$Q = \begin{bmatrix} 0.36 & 0.48 & -0.80 \\ -0.80 & 0.60 & 0.00 \\ 0.48 & 0.64 & 0.60 \end{bmatrix} .$
If acts in a certain direction, , purely as a scaling by a factor , then we have
:$Q \mathbf{v} = \lambda \mathbf{v},$
so that
:$\mathbf{0} = (\lambda I - Q) \mathbf{v} .$
Thus is a root of the characteristic polynomial for ,
:$\begin{align} 0 &{}= \det (\lambda I - Q) \\ &{}= \lambda^3 - \tfrac{39}{25} \lambda^2 + \tfrac{39}{25} \lambda - 1 \\ &{}= (\lambda-1) \left(\lambda^2 - \tfrac{14}{25} \lambda + 1\right). \end{align}$
Two features are noteworthy. First, one of the roots (or eigenvalues) is 1, which tells us that some direction is unaffected by the matrix. For rotations in three dimensions, this is the ''axis'' of the rotation (a concept that has no meaning in any other dimension). Second, the other two roots are a pair of complex conjugates, whose product is 1 (the constant term of the quadratic), and whose sum is (the negated linear term). This factorization is of interest for rotation matrices because the same thing occurs for all of them. (As special cases, for a null rotation the "complex conjugates" are both 1, and for a 180° rotation they are both −1.) Furthermore, a similar factorization holds for any rotation matrix. If the dimension, , is odd, there will be a "dangling" eigenvalue of 1; and for any dimension the rest of the polynomial factors into quadratic terms like the one here (with the two special cases noted). We are guaranteed that the characteristic polynomial will have degree and thus eigenvalues. And since a rotation matrix commutes with its transpose, it is a normal matrix, so can be diagonalized. We conclude that every rotation matrix, when expressed in a suitable coordinate system, partitions into independent rotations of two-dimensional subspaces, at most of them.

The sum of the entries on the main diagonal of a matrix is called the trace; it does not change if we reorient the coordinate system, and always equals the sum of the eigenvalues. This has the convenient implication for and rotation matrices that the trace reveals the angle of rotation, , in the two-dimensional space (or subspace). For a matrix the trace is , and for a matrix it is . In the three-dimensional case, the subspace consists of all vectors perpendicular to the rotation axis (the invariant direction, with eigenvalue 1). Thus we can extract from any rotation matrix a rotation axis and an angle, and these completely determine the rotation.

Sequential angles

The constraints on a rotation matrix imply that it must have the form
:$Q = \begin{bmatrix} a & -b \\ b & a \end{bmatrix}$
with . Therefore, we may set and , for some angle . To solve for it is not enough to look at alone or alone; we must consider both together to place the angle in the correct quadrant, using a two-argument arctangent function.

Now consider the first column of a rotation matrix,
:$\begin{bmatrix}a\\b\\c\end{bmatrix} .$
Although will probably not equal 1, but some value , we can use a slight variation of the previous computation to find a so-called Givens rotation that transforms the column to
:$\begin{bmatrix}r\\0\\c\end{bmatrix} ,$
zeroing . This acts on the subspace spanned by the - and -axes. We can then repeat the process for the -subspace to zero . Acting on the full matrix, these two rotations produce the schematic form
:$Q_{xz}Q_{xy}Q = \begin{bmatrix}1&0&0\\0&\ast&\ast\\0&\ast&\ast\end{bmatrix} .$
Shifting attention to the second column, a Givens rotation of the -subspace can now zero the value. This brings the full matrix to the form
:$Q_{yz}Q_{xz}Q_{xy}Q = \begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix} ,$
which is an identity matrix. Thus we have decomposed as
:$Q = Q_{xy}^{-1}Q_{xz}^{-1}Q_{yz}^{-1} .$

An rotation matrix will have , or
:$\sum_{k=1}^{n-1} k = \frac{1}{2}n(n - 1)$
entries below the diagonal to zero. We can zero them by extending the same idea of stepping through the columns with a series of rotations in a fixed sequence of planes. We conclude that the set of rotation matrices, each of which has entries, can be parameterized by angles.

{, border="1" cellspacing="0" cellpadding="4" style="float:right; margin-left:1em"
, -
, , , , , , ,
, -
, , , , , , ,
, -
, , , , , , ,
, -
, , , , , , ,
, -
, , , , , , ,
, -
, , , , , , ,

In three dimensions this restates in matrix form an observation made by Euler, so mathematicians call the ordered sequence of three angles Euler angles. However, the situation is somewhat more complicated than we have so far indicated. Despite the small dimension, we actually have considerable freedom in the sequence of axis pairs we use; and we also have some freedom in the choice of angles. Thus we find many different conventions employed when three-dimensional rotations are parameterized for physics, or medicine, or chemistry, or other disciplines. When we include the option of world axes or body axes, 24 different sequences are possible. And while some disciplines call any sequence Euler angles, others give different names (Cardano, Tait–Bryan, roll-pitch-yaw) to different sequences.

One reason for the large number of options is that, as noted previously, rotations in three dimensions (and higher) do not commute. If we reverse a given sequence of rotations, we get a different outcome. This also implies that we cannot compose two rotations by adding their corresponding angles. Thus Euler angles are not vectors, despite a similarity in appearance as a triplet of numbers.

Nested dimensions

A rotation matrix such as
:$Q_{3 \times 3} = \begin{bmatrix} \cos \theta & -\sin \theta & {\color{CadetBlue}0} \\ \sin \theta & \cos \theta & {\color{CadetBlue}0} \\ {\color{CadetBlue}0} & {\color{CadetBlue}0} & {\color{CadetBlue}1} \end{bmatrix}$

suggests a rotation matrix,
:$Q_{2 \times 2} = \begin{bmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{bmatrix},$

is embedded in the upper left corner:
:Q_{3 \times 3} = \left \begin{matrix} Q_{2 \times 2} & \mathbf{0} \\ \mathbf{0}^\mathsf{T} & 1 \end{matrix} \right

This is no illusion; not just one, but many, copies of -dimensional rotations are found within -dimensional rotations, as subgroups. Each embedding leaves one direction fixed, which in the case of matrices is the rotation axis. For example, we have
:\begin{align}
Q_{\mathbf{x(\theta) &= \begin{bmatrix}
{\color{CadetBlue}1} & {\color{CadetBlue}0} & {\color{CadetBlue}0} \\
{\color{CadetBlue}0} & \cos \theta & -\sin \theta \\
{\color{CadetBlue}0} & \sin \theta & \cos \theta
\end{bmatrix}, \\ px Q_{\mathbf{y(\theta) &= \begin{bmatrix}
\cos \theta & {\color{CadetBlue}0} & \sin \theta \\
{\color{CadetBlue}0} & {\color{CadetBlue}1} & {\color{CadetBlue}0} \\
-\sin \theta & {\color{CadetBlue}0} & \cos \theta
\end{bmatrix}, \\ px Q_{\mathbf{z(\theta) &= \begin{bmatrix}
\cos \theta & -\sin \theta & {\color{CadetBlue}0} \\
\sin \theta & \cos \theta & {\color{CadetBlue}0} \\
{\color{CadetBlue}0} & {\color{CadetBlue}0} & {\color{CadetBlue}1}
\end{bmatrix},
\end{align}

fixing the -axis, the -axis, and the -axis, respectively. The rotation axis need not be a coordinate axis; if is a unit vector in the desired direction, then
:\begin{align}
Q_\mathbf{u}(\theta)
&= \begin{bmatrix}
0 & -z & y \\
z & 0 & -x \\
-y & x & 0
\end{bmatrix} \sin\theta + \left(I - \mathbf{u}\mathbf{u}^\mathsf{T}\right) \cos\theta + \mathbf{u}\mathbf{u}^\mathsf{T} \\ px &= \begin{bmatrix}
\left(1 - x^2\right) c_\theta + x^2 &
-z s_\theta - x y c_\theta + x y &
y s_\theta - x z c_\theta + x z \\
z s_\theta - x y c_\theta + x y &
\left(1 - y^2\right) c_\theta + y^2 &
-x s_\theta - y z c_\theta + y z \\
-y s_\theta - x z c_\theta + x z &
x s_\theta - y z c_\theta + y z &
\left(1 - z^2\right) c_\theta + z^2
\end{bmatrix} \\ px &= \begin{bmatrix}
x^2 (1 - c_\theta) + c_\theta &
x y (1 - c_\theta) - z s_\theta &
x z (1 - c_\theta) + y s_\theta \\
x y (1 - c_\theta) + z s_\theta &
y^2 (1 - c_\theta) + c_\theta &
y z (1 - c_\theta) - x s_\theta \\
x z (1 - c_\theta) - y s_\theta &
y z (1 - c_\theta) + x s_\theta &
z^2 (1 - c_\theta) + c_\theta
\end{bmatrix},
\end{align}

where , , is a rotation by angle leaving axis fixed.

A direction in -dimensional space will be a unit magnitude vector, which we may consider a point on a generalized sphere, . Thus it is natural to describe the rotation group as combining and . A suitable formalism is the fiber bundle,
:$SO(n) \hookrightarrow SO(n + 1) \to S^n ,$

where for every direction in the base space, , the fiber over it in the total space, , is a copy of the fiber space, , namely the rotations that keep that direction fixed.

Thus we can build an rotation matrix by starting with a matrix, aiming its fixed axis on (the ordinary sphere in three-dimensional space), aiming the resulting rotation on , and so on up through . A point on can be selected using numbers, so we again have numbers to describe any rotation matrix.

In fact, we can view the sequential angle decomposition, discussed previously, as reversing this process. The composition of Givens rotations brings the first column (and row) to , so that the remainder of the matrix is a rotation matrix of dimension one less, embedded so as to leave fixed.

Skew parameters via Cayley's formula

When an rotation matrix , does not include a −1 eigenvalue, thus none of the planar rotations which it comprises are 180° rotations, then is an invertible matrix. Most rotation matrices fit this description, and for them it can be shown that is a skew-symmetric matrix, . Thus ; and since the diagonal is necessarily zero, and since the upper triangle determines the lower one, contains independent numbers.

Conveniently, is invertible whenever is skew-symmetric; thus we can recover the original matrix using the ''Cayley transform'',
:$A \mapsto (I+A)(I-A)^{-1} ,$
which maps any skew-symmetric matrix to a rotation matrix. In fact, aside from the noted exceptions, we can produce any rotation matrix in this way. Although in practical applications we can hardly afford to ignore 180° rotations, the Cayley transform is still a potentially useful tool, giving a parameterization of most rotation matrices without trigonometric functions.

In three dimensions, for example, we have
:\begin{align}
&\begin{bmatrix}
0 & -z & y \\
z & 0 & -x \\
-y & x & 0
\end{bmatrix} \mapsto \\ pt \quad \frac{1}{1 + x^2 + y^2 + z^2}
&\begin{bmatrix}
1 + x^2 - y^2 - z^2 & 2xy - 2z & 2y + 2xz \\
2xy + 2z & 1 - x^2 + y^2 - z^2 & 2yz - 2x \\
2xz - 2y & 2x + 2yz & 1 - x^2 - y^2 + z^2
\end{bmatrix} .
\end{align}

If we condense the skew entries into a vector, , then we produce a 90° rotation around the -axis for (1, 0, 0), around the -axis for (0, 1, 0), and around the -axis for (0, 0, 1). The 180° rotations are just out of reach; for, in the limit as , does approach a 180° rotation around the axis, and similarly for other directions.

Decomposition into shears

For the 2D case, a rotation matrix can be decomposed into three shear matrices ():

:$\begin{align} R(\theta) &{}= \begin{bmatrix} 1 & -\tan \frac{\theta}{2}\\ 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0\\ \sin \theta & 1 \end{bmatrix} \begin{bmatrix} 1 & -\tan \frac{\theta}{2}\\ 0 & 1 \end{bmatrix} \end{align}$

This is useful, for instance, in computer graphics, since shears can be implemented with fewer multiplication instructions than rotating a bitmap directly. On modern computers, this may not matter, but it can be relevant for very old or low-end microprocessors.

A rotation can also be written as two shears and a squeeze mapping (an area preserving scaling) ():

:$\begin{align} R(\theta) &{}= \begin{bmatrix} 1 & 0\\ \tan\theta & 1 \end{bmatrix} \begin{bmatrix} 1 & -\sin\theta\cos\theta\\ 0 & 1 \end{bmatrix} \begin{bmatrix} \cos\theta & 0\\ 0 & \frac{1}{\cos\theta} \end{bmatrix} \end{align}$

Group theory

Below follow some basic facts about the role of the collection of ''all'' rotation matrices of a fixed dimension (here mostly 3) in mathematics and particularly in physics where rotational symmetry is a ''requirement'' of every truly fundamental law (due to the assumption of isotropy of space), and where the same symmetry, when present, is a ''simplifying property'' of many problems of less fundamental nature. Examples abound in classical mechanics and quantum mechanics. Knowledge of the part of the solutions pertaining to this symmetry applies (with qualifications) to ''all'' such problems and it can be factored out of a specific problem at hand, thus reducing its complexity. A prime example – in mathematics and physics – would be the theory of spherical harmonics. Their role in the group theory of the rotation groups is that of being a representation space for the entire set of finite-dimensional irreducible representations of the rotation group SO(3). For this topic, see Rotation group SO(3) § Spherical harmonics.

The main articles listed in each subsection are referred to for more detail.

Lie group

The rotation matrices for each form a group, the special orthogonal group, . This algebraic structure is coupled with a topological structure inherited from $\operatorname{GL}_n(\R)$ in such a way that the operations of multiplication and taking the inverse are analytic functions of the matrix entries. Thus is for each a Lie group. It is compact and connected, but not simply connected. It is also a semi-simple group, in fact a simple group with the exception SO(4). The relevance of this is that all theorems and all machinery from the theory of analytic manifolds (analytic manifolds are in particular smooth manifolds) apply and the well-developed representation theory of compact semi-simple groups is ready for use.

Lie algebra

The Lie algebra of is given by
:$\mathfrak{so}(n) = \mathfrak{o}(n) = \left\{X \in M_n(\mathbb{R}) \mid X = -X^\mathsf{T} \right\},$
and is the space of skew-symmetric matrices of dimension , see classical group, where is the Lie algebra of , the orthogonal group. For reference, the most common basis for is
:$L_{\mathbf{x = \begin{bmatrix}0&0&0\\0&0&-1\\0&1&0\end{bmatrix} , \quad L_{\mathbf{y = \begin{bmatrix}0&0&1\\0&0&0\\-1&0&0\end{bmatrix} , \quad L_{\mathbf{z = \begin{bmatrix}0&-1&0\\1&0&0\\0&0&0\end{bmatrix}.$

Exponential map

Connecting the Lie algebra to the Lie group is the exponential map, which is defined using the standard matrix exponential series for For any skew-symmetric matrix , is always a rotation matrix.Note that this exponential map of skew-symmetric matrices to rotation matrices is quite different from the Cayley transform discussed earlier, differing to the third order,
:$e^{2A} - \frac{I+A}{I-A}=- \tfrac{2}{3} A^3 +\mathrm{O} \left(A^4\right) .$
Conversely, a skew-symmetric matrix specifying a rotation matrix through the Cayley map specifies the ''same'' rotation matrix through the map .

An important practical example is the case. In rotation group SO(3), it is shown that one can identify every with an Euler vector , where is a unit magnitude vector.

By the properties of the identification $\mathbf{su}(2) \cong \mathbb{R}^3$, is in the null space of . Thus, is left invariant by and is hence a rotation axis.

According to Rodrigues' rotation formula on matrix form, one obtains,

:$\begin{align} \exp( A ) &= \exp\bigl(\theta(\mathbf{u}\cdot\mathbf{L})\bigr) \\ &= \exp \left( \begin{bmatrix} 0 & -z \theta & y \theta \\ z \theta & 0&-x \theta \\ -y \theta & x \theta & 0 \end{bmatrix} \right) \\ &= I + \sin \theta \ \mathbf{u}\cdot\mathbf{L} + (1-\cos \theta)(\mathbf{u}\cdot\mathbf{L} )^2 , \end{align}$

where
: $\mathbf{u}\cdot\mathbf{L} = \begin{bmatrix} 0 & -z & y \\ z & 0&-x \\ -y & x & 0 \end{bmatrix} .$

This is the matrix for a rotation around axis by the angle . For full detail, see exponential map SO(3).

Baker–Campbell–Hausdorff formula

The BCH formula provides an explicit expression for in terms of a series expansion of nested commutators of and . This general expansion unfolds asFor a detailed derivation, see Derivative of the exponential map. Issues of convergence of this series to the right element of the Lie algebra are here swept under the carpet. Convergence is guaranteed when and . If these conditions are not fulfilled, the series may still converge. A solution always exists since is onto in the cases under consideration.
:$Z = C(X, Y) = X + Y + \tfrac{1}{2}$, Y+ \tfrac{1}{12} \bigl ,[X,Ybigr">,Y.html" ;"title=",[X,Y">,[X,Ybigr- \tfrac{1}{12} \bigl[Y,[X,Y">,Y">,[X,Y<_a>bigr.html" ;"title=",Y.html" ;"title=",[X,Y">,[X,Ybigr">,Y.html" ;"title=",[X,Y">,[X,Ybigr- \tfrac{1}{12} \bigl[Y,[X,Ybigr] + \cdots .

In the case, the general infinite expansion has a compact form,
:$Z = \alpha X + \beta Y + \gamma[X, Y],$
for suitable trigonometric function coefficients, detailed in the Baker–Campbell–Hausdorff formula for SO(3).

As a group identity, the above holds for ''all faithful representations'', including the doublet (spinor representation), which is simpler. The same explicit formula thus follows straightforwardly through Pauli matrices; see the derivation for SU(2). For the general case, one might use Ref.

Spin group

The Lie group of rotation matrices, , is not simply connected, so Lie theory tells us it is a homomorphic image of a universal covering group. Often the covering group, which in this case is called the spin group denoted by , is simpler and more natural to work with.

In the case of planar rotations, SO(2) is topologically a circle, . Its universal covering group, Spin(2), is isomorphic to the real line, , under addition. Whenever angles of arbitrary magnitude are used one is taking advantage of the convenience of the universal cover. Every rotation matrix is produced by a countable infinity of angles, separated by integer multiples of 2. Correspondingly, the fundamental group of is isomorphic to the integers, .

In the case of spatial rotations, SO(3) is topologically equivalent to three-dimensional real projective space, . Its universal covering group, Spin(3), is isomorphic to the , . Every rotation matrix is produced by two opposite points on the sphere. Correspondingly, the fundamental group of SO(3) is isomorphic to the two-element group, .

We can also describe Spin(3) as isomorphic to quaternions of unit norm under multiplication, or to certain real matrices, or to complex special unitary matrices, namely SU(2). The covering maps for the first and the last case are given by
:$\mathbb{H} \supset \{q \in \mathbb{H}: \, q\, = 1\} \ni w + \mathbf{i}x + \mathbf{j}y + \mathbf{k}z \mapsto \begin{bmatrix} 1 - 2 y^2 - 2 z^2 & 2 x y - 2 z w & 2 x z + 2 y w \\ 2 x y + 2 z w & 1 - 2 x^2 - 2 z^2 & 2 y z - 2 x w \\ 2 x z - 2 y w & 2 y z + 2 x w & 1 - 2 x^2 - 2 y^2 \end{bmatrix} \in \mathrm{SO}(3),$
and
:$\mathrm{SU}(2) \ni \begin{bmatrix} \alpha & \beta \\ -\overline{\beta} & \overline{\alpha} \end{bmatrix} \mapsto \begin{bmatrix} \frac{1}{2}\left(\alpha^2 - \beta^2 + \overline{\alpha^2} - \overline{\beta^2}\right) & \frac{i}{2}\left(-\alpha^2 - \beta^2 + \overline{\alpha^2} + \overline{\beta^2}\right) & -\alpha\beta - \overline{\alpha}\overline{\beta} \\ \frac{i}{2}\left(\alpha^2 - \beta^2 - \overline{\alpha^2} + \overline{\beta^2}\right) & \frac{i}{2}\left(\alpha^2 + \beta^2 + \overline{\alpha^2} + \overline{\beta^2}\right) & -i\left(+\alpha\beta - \overline{\alpha}\overline{\beta}\right) \\ \alpha\overline{\beta} + \overline{\alpha}\beta & i\left(-\alpha\overline{\beta} + \overline{\alpha}\beta\right) & \alpha\overline{\alpha} - \beta\overline{\beta} \end{bmatrix} \in \mathrm{SO}(3).$

For a detailed account of the and the quaternionic covering, see spin group SO(3).

Many features of these cases are the same for higher dimensions. The coverings are all two-to-one, with , , having fundamental group . The natural setting for these groups is within a Clifford algebra. One type of action of the rotations is produced by a kind of "sandwich", denoted by . More importantly in applications to physics, the corresponding spin representation of the Lie algebra sits inside the Clifford algebra. It can be exponentiated in the usual way to give rise to a representation, also known as projective representation of the rotation group. This is the case with SO(3) and SU(2), where the representation can be viewed as an "inverse" of the covering map. By properties of covering maps, the inverse can be chosen ono-to-one as a local section, but not globally.

Infinitesimal rotations

The matrices in the Lie algebra are not themselves rotations; the skew-symmetric matrices are derivatives, proportional differences of rotations. An actual "differential rotation", or ''infinitesimal rotation matrix'' has the form
:$I + A \, d\theta ,$
where is vanishingly small and , for instance with ,
:$dL_{x} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & -d\theta \\ 0 & d\theta & 1 \end{bmatrix}.$

The computation rules are as usual except that infinitesimals of second order are routinely dropped. With these rules, these matrices do not satisfy all the same properties as ordinary finite rotation matrices under the usual treatment of infinitesimals. It turns out that ''the order in which infinitesimal rotations are applied is irrelevant''. To see this exemplified, consult infinitesimal rotations SO(3).

Conversions

We have seen the existence of several decompositions that apply in any dimension, namely independent planes, sequential angles, and nested dimensions. In all these cases we can either decompose a matrix or construct one. We have also given special attention to rotation matrices, and these warrant further attention, in both directions .

Quaternion

Given the unit quaternion , the equivalent pre-multiplied (to be used with column vectors) rotation matrix is
:$Q = \begin{bmatrix} 1 - 2 y^2 - 2 z^2 & 2 x y - 2 z w & 2 x z + 2 y w \\ 2 x y + 2 z w & 1 - 2 x^2 - 2 z^2 & 2 y z - 2 x w \\ 2 x z - 2 y w & 2 y z + 2 x w & 1 - 2 x^2 - 2 y^2 \end{bmatrix} .$

Now every quaternion component appears multiplied by two in a term of degree two, and if all such terms are zero what is left is an identity matrix. This leads to an efficient, robust conversion from any quaternion – whether unit or non-unit – to a rotation matrix. Given:
:$\begin{align} n &= w \times w + x \times x + y \times y + z \times z \\ s &= \begin{cases} 0 &\text{if } n = 0 \\ \frac{2}{n} &\text{otherwise} \end{cases} \\ \end{align}$
we can calculate
:$Q = \begin{bmatrix} 1 - s(yy + zz) & s(xy - wz) & s(xz + wy) \\ s(xy + wz) & 1 - s(xx + zz) & s(yz - wx) \\ s(xz - wy) & s(yz + wx) & 1 - s(xx + yy) \end{bmatrix}$

Freed from the demand for a unit quaternion, we find that nonzero quaternions act as homogeneous coordinates for rotation matrices. The Cayley transform, discussed earlier, is obtained by scaling the quaternion so that its component is 1. For a 180° rotation around any axis, will be zero, which explains the Cayley limitation.

The sum of the entries along the main diagonal (the trace), plus one, equals , which is . Thus we can write the trace itself as ; and from the previous version of the matrix we see that the diagonal entries themselves have the same form: , , and . So we can easily compare the magnitudes of all four quaternion components using the matrix diagonal. We can, in fact, obtain all four magnitudes using sums and square roots, and choose consistent signs using the skew-symmetric part of the off-diagonal entries:
:$\begin{align} t &= \operatorname{tr} Q = Q_{xx} + Q_{yy} + Q_{zz} \quad (\text{the trace of }Q) \\ r &= \sqrt{1 + t} \\ w &= \tfrac{1}{2} r \\ x &= \operatorname{sgn}\left(Q_{zy} - Q_{yz}\right)\left, \tfrac12 \sqrt{1 + Q_{xx} - Q_{yy} - Q_{zz\ \\ y &= \operatorname{sgn}\left(Q_{xz} - Q_{zx}\right)\left, \tfrac12 \sqrt{1 - Q_{xx} + Q_{yy} - Q_{zz\ \\ z &= \operatorname{sgn}\left(Q_{yx} - Q_{xy}\right)\left, \tfrac12 \sqrt{1 - Q_{xx} - Q_{yy} + Q_{zz\ \end{align}$

Alternatively, use a single square root and division
:$\begin{align} t &= \operatorname{tr} Q = Q_{xx} + Q_{yy} + Q_{zz} \\ r &= \sqrt{1 + t} \\ s &= \tfrac{1}{2r} \\ w &= \tfrac{1}{2} r \\ x &= \left(Q_{zy} - Q_{yz}\right)s \\ y &= \left(Q_{xz} - Q_{zx}\right)s \\ z &= \left(Q_{yx} - Q_{xy}\right)s \end{align}$

This is numerically stable so long as the trace, , is not negative; otherwise, we risk dividing by (nearly) zero. In that case, suppose is the largest diagonal entry, so will have the largest magnitude (the other cases are derived by cyclic permutation); then the following is safe.
:$\begin{align} r &= \sqrt{1 + Q_{xx} - Q_{yy} - Q_{zz \\ s &= \tfrac{1}{2r} \\ w &= \left(Q_{zy} - Q_{yz}\right)s \\ x &= \tfrac12 r \\ y &= \left(Q_{xy} + Q_{yx}\right)s \\ z &= \left(Q_{zx} + Q_{xz}\right)s \end{align}$

If the matrix contains significant error, such as accumulated numerical error, we may construct a symmetric matrix,
:$K = \frac13 \begin{bmatrix} Q_{xx}-Q_{yy}-Q_{zz} & Q_{yx}+Q_{xy} & Q_{zx}+Q_{xz} & Q_{zy}-Q_{yz} \\ Q_{yx}+Q_{xy} & Q_{yy}-Q_{xx}-Q_{zz} & Q_{zy}+Q_{yz} & Q_{xz}-Q_{zx} \\ Q_{zx}+Q_{xz} & Q_{zy}+Q_{yz} & Q_{zz}-Q_{xx}-Q_{yy} & Q_{yx}-Q_{xy} \\ Q_{zy}-Q_{yz} & Q_{xz}-Q_{zx} & Q_{yx}-Q_{xy} & Q_{xx}+Q_{yy}+Q_{zz} \end{bmatrix} ,$
and find the eigenvector, , of its largest magnitude eigenvalue. (If is truly a rotation matrix, that value will be 1.) The quaternion so obtained will correspond to the rotation matrix closest to the given matrix (Note: formulation of the cited article is post-multiplied, works with row vectors).

Polar decomposition

If the matrix is nonsingular, its columns are linearly independent vectors; thus the Gram–Schmidt process can adjust them to be an orthonormal basis. Stated in terms of numerical linear algebra, we convert to an orthogonal matrix, , using QR decomposition. However, we often prefer a closest to , which this method does not accomplish. For that, the tool we want is the polar decomposition (; ).

To measure closeness, we may use any matrix norm invariant under orthogonal transformations. A convenient choice is the Frobenius norm, , squared, which is the sum of the squares of the element differences. Writing this in terms of the trace, , our goal is,
: Find minimizing , subject to .

Though written in matrix terms, the objective function is just a quadratic polynomial. We can minimize it in the usual way, by finding where its derivative is zero. For a matrix, the orthogonality constraint implies six scalar equalities that the entries of must satisfy. To incorporate the constraint(s), we may employ a standard technique, Lagrange multipliers, assembled as a symmetric matrix, . Thus our method is:
: Differentiate with respect to (the entries of) , and equate to zero.

Consider a example. Including constraints, we seek to minimize
:$\begin{align} &\left(Q_{xx} - M_{xx}\right)^2 + \left(Q_{xy} - M_{xy}\right)^2 + \left(Q_{yx} - M_{yx}\right)^2 + \left(Q_{yy} - M_{yy}\right)^2 \\ &\quad {}+ \left(Q_{xx}^2 + Q_{yx}^2 - 1\right)Y_{xx} + \left(Q_{xy}^2 + Q_{yy}^2 - 1\right)Y_{yy} + 2\left(Q_{xx} Q_{xy} + Q_{yx} Q_{yy}\right)Y_{xy} . \end{align}$

Taking the derivative with respect to , , , in turn, we assemble a matrix.
:$2\begin{bmatrix} Q_{xx} - M_{xx} + Q_{xx} Y_{xx} + Q_{xy} Y_{xy} & Q_{xy} - M_{xy} + Q_{xx} Y_{xy} + Q_{xy} Y_{yy} \\ Q_{yx} - M_{yx} + Q_{yx} Y_{xx} + Q_{yy} Y_{xy} & Q_{yy} - M_{yy} + Q_{yx} Y_{xy} + Q_{yy} Y_{yy} \end{bmatrix}$

In general, we obtain the equation
:$0 = 2(Q - M) + 2QY ,$
so that
:$M = Q(I + Y) = QS ,$
where is orthogonal and is symmetric. To ensure a minimum, the matrix (and hence ) must be positive definite. Linear algebra calls the polar decomposition of , with the positive square root of .
:$S^2 = \left(Q^\mathsf{T} M\right)^\mathsf{T} \left(Q^\mathsf{T} M\right) = M^\mathsf{T} Q Q^\mathsf{T} M = M^\mathsf{T} M$

When is non-singular, the and factors of the polar decomposition are uniquely determined. However, the determinant of is positive because is positive definite, so inherits the sign of the determinant of . That is, is only guaranteed to be orthogonal, not a rotation matrix. This is unavoidable; an with negative determinant has no uniquely defined closest rotation matrix.

Axis and angle

To efficiently construct a rotation matrix from an angle and a unit axis , we can take advantage of symmetry and skew-symmetry within the entries. If , , and are the components of the unit vector representing the axis, and

:$\begin{align} c &= \cos \theta\\ s &= \sin \theta\\ C &= 1-c \end{align}$

then

:$Q(\theta) = \begin{bmatrix} xxC+c & xyC-zs & xzC+ys\\ yxC+zs & yyC+c & yzC-xs\\ zxC-ys & zyC+xs & zzC+c \end{bmatrix}$

Determining an axis and angle, like determining a quaternion, is only possible up to the sign; that is, and correspond to the same rotation matrix, just like and . Additionally, axis–angle extraction presents additional difficulties. The angle can be restricted to be from 0° to 180°, but angles are formally ambiguous by multiples of 360°. When the angle is zero, the axis is undefined. When the angle is 180°, the matrix becomes symmetric, which has implications in extracting the axis. Near multiples of 180°, care is needed to avoid numerical problems: in extracting the angle, a two-argument arctangent with equal to avoids the insensitivity of arccos; and in computing the axis magnitude in order to force unit magnitude, a brute-force approach can lose accuracy through underflow .

A partial approach is as follows:

:$\begin{align} x &= Q_{zy} - Q_{yz}\\ y &= Q_{xz} - Q_{zx}\\ z &= Q_{yx} - Q_{xy}\\ r &= \sqrt{x^2 + y^2 + z^2}\\ t &= Q_{xx} + Q_{yy} + Q_{zz}\\ \theta &= \operatorname{atan2}(r,t-1)\end{align}$

The -, -, and -components of the axis would then be divided by . A fully robust approach will use a different algorithm when , the trace of the matrix , is negative, as with quaternion extraction. When is zero because the angle is zero, an axis must be provided from some source other than the matrix.

Euler angles

Complexity of conversion escalates with Euler angles (used here in the broad sense). The first difficulty is to establish which of the twenty-four variations of Cartesian axis order we will use. Suppose the three angles are , , ; physics and chemistry may interpret these as

:$Q(\theta_1,\theta_2,\theta_3)= Q_{\mathbf{z(\theta_1) Q_{\mathbf{y(\theta_2) Q_{\mathbf{z(\theta_3) ,$

while aircraft dynamics may use
:$Q(\theta_1,\theta_2,\theta_3)= Q_{\mathbf{z(\theta_3) Q_{\mathbf{y(\theta_2) Q_{\mathbf{x(\theta_1) .$
One systematic approach begins with choosing the rightmost axis. Among all permutations of , only two place that axis first; one is an even permutation and the other odd. Choosing parity thus establishes the middle axis. That leaves two choices for the left-most axis, either duplicating the first or not. These three choices gives us variations; we double that to 24 by choosing static or rotating axes.

This is enough to construct a matrix from angles, but triples differing in many ways can give the same rotation matrix. For example, suppose we use the convention above; then we have the following equivalent pairs:
:{, style="text-align:right"
, (90°,, , 45°,, , −105°) , , ≡ , , (−270°,, , −315°,, , 255°) , , ''multiples of 360°''
, -
, (72°,, , 0°,, , 0°) , , ≡ , , (40°,, , 0°,, , 32°) , , ''singular alignment''
, -
, (45°,, , 60°,, , −30°) , , ≡ , , (−135°,, , −60°,, , 150°) , , ''bistable flip''

Angles for any order can be found using a concise common routine (; ).

The problem of singular alignment, the mathematical analog of physical gimbal lock, occurs when the middle rotation aligns the axes of the first and last rotations. It afflicts every axis order at either even or odd multiples of 90°. These singularities are not characteristic of the rotation matrix as such, and only occur with the usage of Euler angles.

The singularities are avoided when considering and manipulating the rotation matrix as orthonormal row vectors (in 3D applications often named the right-vector, up-vector and out-vector) instead of as angles. The singularities are also avoided when working with quaternions.

Vector to vector formulation

In some instances it is interesting to describe a rotation by specifying how a vector is mapped into another through the shortest path (smallest angle). In $\mathbb{R}^3$ this completely describes the associated rotation matrix. In general, given , the matrix
:$R:=I+y x^\mathsf{T}-x y^\mathsf{T}+\frac{1}{1+\langle x,y\rangle}\left(yx^\mathsf{T}-xy^\mathsf{T}\right)^2$
belongs to and maps to .

Voigt notation

In materials science, the four-dimensional stiffness and compliance tensors are often simplified to a two-dimensional matrix using Voigt notation. When applying a rotational transform through angle $\theta$ in this notation, the rotation matrix is given byClyne, T. W., & Hull, D. (2019). Tensor Analysis of Anisotropic Materials and the Elastic Deformation of Laminae. In An Introduction to Composite Materials (pp. 43–66). chapter, Cambridge: Cambridge University Press.

:$T = \begin{bmatrix} \cos^2\theta & \sin^2\theta & 2\sin\theta\cos\theta \\ \sin^2\theta & \cos^2\theta & 2\sin\theta\cos\theta \\ -\sin\theta\cos\theta & \sin\theta\cos\theta & \cos^2\theta - \sin^2\theta \end{bmatrix} .$

This is particularly useful in composite laminate design, where plies are often rotated by a certain angle to bring the properties of the laminate closer to isotropic.

Uniform random rotation matrices

We sometimes need to generate a uniformly distributed random rotation matrix. It seems intuitively clear in two dimensions that this means the rotation angle is uniformly distributed between 0 and 2. That intuition is correct, but does not carry over to higher dimensions. For example, if we decompose rotation matrices in axis–angle form, the angle should ''not'' be uniformly distributed; the probability that (the magnitude of) the angle is at most should be , for .

Since is a connected and locally compact Lie group, we have a simple standard criterion for uniformity, namely that the distribution be unchanged when composed with any arbitrary rotation (a Lie group "translation"). This definition corresponds to what is called ''Haar measure''. show how to use the Cayley transform to generate and test matrices according to this criterion.

We can also generate a uniform distribution in any dimension using the ''subgroup algorithm'' of . This recursively exploits the nested dimensions group structure of , as follows. Generate a uniform angle and construct a rotation matrix. To step from to , generate a vector uniformly distributed on the -sphere , embed the matrix in the next larger size with last column , and rotate the larger matrix so the last column becomes .

As usual, we have special alternatives for the case. Each of these methods begins with three independent random scalars uniformly distributed on the unit interval. takes advantage of the odd dimension to change a Householder reflection to a rotation by negation, and uses that to aim the axis of a uniform planar rotation.

Another method uses unit quaternions. Multiplication of rotation matrices is homomorphic to multiplication of quaternions, and multiplication by a unit quaternion rotates the unit sphere. Since the homomorphism is a local isometry, we immediately conclude that to produce a uniform distribution on SO(3) we may use a uniform distribution on . In practice: create a four-element vector where each element is a sampling of a normal distribution. Normalize its length and you have a uniformly sampled random unit quaternion which represents a uniformly sampled random rotation. Note that the aforementioned only applies to rotations in dimension 3. For a generalised idea of quaternions, one should look into Rotors.

Euler angles can also be used, though not with each angle uniformly distributed (; ).

For the axis–angle form, the axis is uniformly distributed over the unit sphere of directions, , while the angle has the nonuniform distribution over noted previously .

See also

* Euler–Rodrigues formula
* Euler's rotation theorem
* Rodrigues' rotation formula
* Plane of rotation
* Axis–angle representation
* Rotation group SO(3)
* Rotation formalisms in three dimensions
* Rotation operator (vector space)
* Transformation matrix
* Yaw-pitch-roll system
* Kabsch algorithm
* Isometry
* Rigid transformation
* Rotations in 4-dimensional Euclidean space
* Trigonometric Identities
* Versor

Remarks

Notes

References

*
*
*
*
* ; reprinted as article 52 in
*
*
*
*
*
* ( GTM 222)
*
*
*
*
*
*
*
*
*
*
*
*
*
*
* (Als
NASA-CR-53568
)
* ( GTM 102)
*

External links

*

Rotation matrices at Mathworld


(requires Java)

Rotation Matrices
at MathPages
*
A parametrization of SOn(R) by generalized Euler Angles

Rotation about any point

{{Matrix classes

Transformation (function)
Matrices (mathematics)
Mathematical physics