Problem of Apollonius

In Euclidean plane geometry, Apollonius's problem is to construct circles that are tangent to three given circles in a plane (Figure 1). Apollonius of Perga (c. 262 190 BC) posed and solved this famous problem in his work (', "Tangencies"); this work has been lost, but a 4th-century AD report of his results by Pappus of Alexandria has survived. Three given circles generically have eight different circles that are tangent to them (Figure 2), a pair of solutions for each way to divide the three given circles in two subsets (there are 4 ways to divide a set of cardinality 3 in 2 parts).

In the 16th century, Adriaan van Roomen solved the problem using intersecting hyperbolas, but this solution does not use only straightedge and compass constructions. François Viète found such a solution by exploiting limiting cases: any of the three given circles can be shrunk to zero radius (a point) or expanded to infinite radius (a line). Viète's approach, which uses simpler limiting cases to solve more complicated ones, is considered a plausible reconstruction of Apollonius' method. The method of van Roomen was simplified by Isaac Newton, who showed that Apollonius' problem is equivalent to finding a position from the differences of its distances to three known points. This has applications in navigation and positioning systems such as LORAN.

Later mathematicians introduced algebraic methods, which transform a geometric problem into algebraic equations. These methods were simplified by exploiting symmetries inherent in the problem of Apollonius: for instance solution circles generically occur in pairs, with one solution enclosing the given circles that the other excludes (Figure 2). Joseph Diaz Gergonne used this symmetry to provide an elegant straightedge and compass solution, while other mathematicians used geometrical transformations such as reflection in a circle to simplify the configuration of the given circles. These developments provide a geometrical setting for algebraic methods (using Lie sphere geometry) and a classification of solutions according to 33 essentially different configurations of the given circles.

Apollonius' problem has stimulated much further work. Generalizations to three dimensions—constructing a sphere tangent to four given spheres—and beyond have been studied. The configuration of three mutually tangent circles has received particular attention. René Descartes gave a formula relating the radii of the solution circles and the given circles, now known as Descartes' theorem. Solving Apollonius' problem iteratively in this case leads to the Apollonian gasket, which is one of the earliest fractals to be described in print, and is important in number theory via Ford circles and the Hardy–Littlewood circle method.

Statement of the problem

The general statement of Apollonius' problem is to construct one or more circles that are tangent to three given objects in a plane, where an object may be a line, a point or a circle of any size. These objects may be arranged in any way and may cross one another; however, they are usually taken to be distinct, meaning that they do not coincide. Solutions to Apollonius' problem are sometimes called ''Apollonius circles'', although the term is also used for other types of circles associated with Apollonius.

The property of tangency is defined as follows. First, a point, line or circle is assumed to be tangent to itself; hence, if a given circle is already tangent to the other two given objects, it is counted as a solution to Apollonius' problem. Two distinct geometrical objects are said to ''intersect'' if they have a point in common. By definition, a point is tangent to a circle or a line if it intersects them, that is, if it lies on them; thus, two distinct points cannot be tangent. If the angle between lines or circles at an intersection point is zero, they are said to be ''tangent''; the intersection point is called a ''tangent point'' or a ''point of tangency''. (The word "tangent" derives from the Latin present participle, ''tangens'', meaning "touching".) In practice, two distinct circles are tangent if they intersect at only one point; if they intersect at zero or two points, they are not tangent. The same holds true for a line and a circle. Two distinct lines cannot be tangent in the plane, although two parallel lines can be considered as tangent at a point at infinity in inversive geometry (see below).

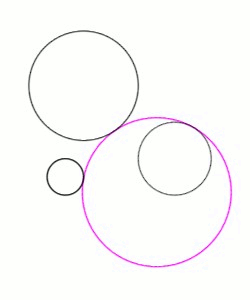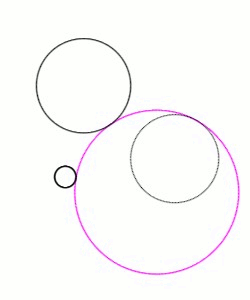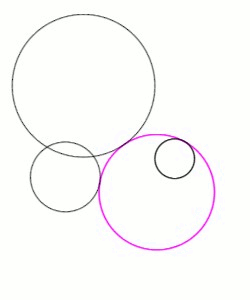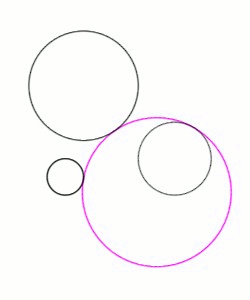
The solution circle may be either internally or externally tangent to each of the given circles. An ''external'' tangency is one where the two circles bend away from each other at their point of contact; they lie on opposite sides of the tangent line at that point, and they exclude one another. The distance between their centers equals the sum of their radii. By contrast, an ''internal'' tangency is one in which the two circles curve in the same way at their point of contact; the two circles lie on the same side of the tangent line, and one circle encloses the other. In this case, the distance between their centers equals the difference of their radii. As an illustration, in Figure 1, the pink solution circle is internally tangent to the medium-sized given black circle on the right, whereas it is externally tangent to the smallest and largest given circles on the left.

Apollonius' problem can also be formulated as the problem of locating one or more points such that the ''differences'' of its distances to three given points equal three known values. Consider a solution circle of radius ''r''_''s'' and three given circles of radii ''r''₁, ''r''₂ and ''r''₃. If the solution circle is externally tangent to all three given circles, the distances between the center of the solution circle and the centers of the given circles equal , and , respectively. Therefore, differences in these distances are constants, such as ; they depend only on the known radii of the given circles and not on the radius ''r''_''s'' of the solution circle, which cancels out. This second formulation of Apollonius' problem can be generalized to internally tangent solution circles (for which the center-center distance equals the difference of radii), by changing the corresponding differences of distances to sums of distances, so that the solution-circle radius ''r''_''s'' again cancels out. The re-formulation in terms of center-center distances is useful in the solutions below of Adriaan van Roomen and Isaac Newton, and also in hyperbolic positioning or trilateration, which is the task of locating a position from differences in distances to three known points. For example, navigation systems such as LORAN identify a receiver's position from the differences in arrival times of signals from three fixed positions, which correspond to the differences in distances to those transmitters.

History

A rich repertoire of geometrical and algebraic methods have been developed to solve Apollonius' problem, which has been called "the most famous of all" geometry problems. The original approach of Apollonius of Perga has been lost, but reconstructions have been offered by François Viète and others, based on the clues in the description by Pappus of Alexandria. The first new solution method was published in 1596 by Adriaan van Roomen, who identified the centers of the solution circles as the intersection points of two hyperbolas. Van Roomen's method was refined in 1687 by Isaac Newton in his '' Principia'', and by John Casey in 1881.

Although successful in solving Apollonius' problem, van Roomen's method has a drawback. A prized property in classical Euclidean geometry is the ability to solve problems using only a compass and a straightedge. Many constructions are impossible using only these tools, such as dividing an angle in three equal parts. However, many such "impossible" problems can be solved by intersecting curves such as hyperbolas, ellipses and parabolas (conic sections). For example, doubling the cube (the problem of constructing a cube of twice the volume of a given cube) cannot be done using only a straightedge and compass, but Menaechmus showed that the problem can be solved by using the intersections of two parabolas. Therefore, van Roomen's solution—which uses the intersection of two hyperbolas—did not determine if the problem satisfied the straightedge-and-compass property.

Van Roomen's friend François Viète, who had urged van Roomen to work on Apollonius' problem in the first place, developed a method that used only compass and straightedge. Prior to Viète's solution, Regiomontanus doubted whether Apollonius' problem could be solved by straightedge and compass. Viète first solved some simple special cases of Apollonius' problem, such as finding a circle that passes through three given points which has only one solution if the points are distinct; he then built up to solving more complicated special cases, in some cases by shrinking or swelling the given circles. According to the 4th-century report of Pappus, Apollonius' own book on this problem—entitled (', "Tangencies"; Latin: ''De tactionibus'', ''De contactibus'')—followed a similar progressive approach. Hence, Viète's solution is considered to be a plausible reconstruction of Apollonius' solution, although other reconstructions have been published independently by three different authors. Simson R (1734) ''Mathematical Collection'', volume VII, p. 117.

Several other geometrical solutions to Apollonius' problem were developed in the 19th century. The most notable solutions are those of Jean-Victor Poncelet (1811) and of Joseph Diaz Gergonne (1814). Whereas Poncelet's proof relies on homothetic centers of circles and the power of a point theorem, Gergonne's method exploits the conjugate relation between lines and their poles in a circle. Methods using circle inversion were pioneered by Julius Petersen in 1879; one example is the annular solution method of HSM Coxeter. Another approach uses Lie sphere geometry, which was developed by Sophus Lie.

Algebraic solutions to Apollonius' problem were pioneered in the 17th century by René Descartes and Princess Elisabeth of Bohemia, although their solutions were rather complex. Practical algebraic methods were developed in the late 18th and 19th centuries by several mathematicians, including Leonhard Euler, Nicolas Fuss, Carl Friedrich Gauss, Lazare Carnot,
and Augustin Louis Cauchy.

Solution methods

Intersecting hyperbolas

The solution of Adriaan van Roomen (1596) is based on the intersection of two hyperbolas. Let the given circles be denoted as ''C''₁, ''C''₂ and ''C''₃. Van Roomen solved the general problem by solving a simpler problem, that of finding the circles that are tangent to ''two'' given circles, such as ''C''₁ and ''C''₂. He noted that the center of a circle tangent to both given circles must lie on a hyperbola whose foci are the centers of the given circles. To understand this, let the radii of the solution circle and the two given circles be denoted as ''r''_''s'', ''r''_''1'' and ''r''_''2'', respectively (Figure 3). The distance ''d''₁ between the centers of the solution circle and ''C''₁ is either or , depending on whether these circles are chosen to be externally or internally tangent, respectively. Similarly, the distance ''d''₂ between the centers of the solution circle and ''C''₂ is either or , again depending on their chosen tangency. Thus, the difference between these distances is always a constant that is independent of ''r''_''s''. This property, of having a fixed difference between the distances to the foci, characterizes hyperbolas, so the possible centers of the solution circle lie on a hyperbola. A second hyperbola can be drawn for the pair of given circles ''C''₂ and ''C''₃, where the internal or external tangency of the solution and ''C''₂ should be chosen consistently with that of the first hyperbola. An intersection of these two hyperbolas (if any) gives the center of a solution circle that has the chosen internal and external tangencies to the three given circles. The full set of solutions to Apollonius' problem can be found by considering all possible combinations of internal and external tangency of the solution circle to the three given circles.

Isaac Newton (1687) refined van Roomen's solution, so that the solution-circle centers were located at the intersections of a line with a circle. Newton formulates Apollonius' problem as a problem in trilateration: to locate a point Z from three given points A, B and C, such that the differences in distances from Z to the three given points have known values. These four points correspond to the center of the solution circle (Z) and the centers of the three given circles (A, B and C).

Instead of solving for the two hyperbolas, Newton constructs their directrix lines instead. For any hyperbola, the ratio of distances from a point Z to a focus A and to the directrix is a fixed constant called the eccentricity. The two directrices intersect at a point T, and from their two known distance ratios, Newton constructs a line passing through T on which Z must lie. However, the ratio of distances TZ/TA is also known; hence, Z also lies on a known circle, since Apollonius had shown that a circle can be defined as the set of points that have a given ratio of distances to two fixed points. (As an aside, this definition is the basis of bipolar coordinates.) Thus, the solutions to Apollonius' problem are the intersections of a line with a circle.

Viète's reconstruction

As described below, Apollonius' problem has ten special cases, depending on the nature of the three given objects, which may be a circle (C), line (L) or point (P). By custom, these ten cases are distinguished by three letter codes such as CCP. Viète solved all ten of these cases using only compass and straightedge constructions, and used the solutions of simpler cases to solve the more complex cases.

Viète began by solving the PPP case (three points) following the method of Euclid in his ''Elements''. From this, he derived a lemma corresponding to the power of a point theorem, which he used to solve the LPP case (a line and two points). Following Euclid a second time, Viète solved the LLL case (three lines) using the angle bisectors. He then derived a lemma for constructing the line perpendicular to an angle bisector that passes through a point, which he used to solve the LLP problem (two lines and a point). This accounts for the first four cases of Apollonius' problem, those that do not involve circles.

To solve the remaining problems, Viète exploited the fact that the given circles and the solution circle may be re-sized in tandem while preserving their tangencies (Figure 4). If the solution-circle radius is changed by an amount Δ''r'', the radius of its internally tangent given circles must be likewise changed by Δ''r'', whereas the radius of its externally tangent given circles must be changed by −Δ''r''. Thus, as the solution circle swells, the internally tangent given circles must swell in tandem, whereas the externally tangent given circles must shrink, to maintain their tangencies.

Viète used this approach to shrink one of the given circles to a point, thus reducing the problem to a simpler, already solved case. He first solved the CLL case (a circle and two lines) by shrinking the circle into a point, rendering it an LLP case. He then solved the CLP case (a circle, a line and a point) using three lemmas. Again shrinking one circle to a point, Viète transformed the CCL case into a CLP case. He then solved the CPP case (a circle and two points) and the CCP case (two circles and a point), the latter case by two lemmas. Finally, Viète solved the general CCC case (three circles) by shrinking one circle to a point, rendering it a CCP case.

Algebraic solutions

Apollonius' problem can be framed as a system of three equations for the center and radius of the solution circle. Since the three given circles and any solution circle must lie in the same plane, their positions can be specified in terms of the (''x'', ''y'') coordinates of their centers. For example, the center positions of the three given circles may be written as (''x''₁, ''y''₁), (''x''₂, ''y''₂) and (''x''₃, ''y''₃), whereas that of a solution circle can be written as (''x''_''s'', ''y''_''s''). Similarly, the radii of the given circles and a solution circle can be written as ''r''₁, ''r''₂, ''r''₃ and ''r''_''s'', respectively. The requirement that a solution circle must exactly touch each of the three given circles can be expressed as three coupled quadratic equations for ''x''_''s'', ''y''_''s'' and ''r''_''s'':

: $\left( x_s - x_1 \right)^2 + \left( y_s - y_1 \right)^2 = \left( r_s - s_1 r_1 \right)^2$

: $\left( x_s - x_2 \right)^2 + \left( y_s - y_2 \right)^2 = \left( r_s - s_2 r_2 \right)^2$

: $\left( x_s - x_3 \right)^2 + \left( y_s - y_3 \right)^2 = \left( r_s - s_3 r_3 \right)^2.$

The three numbers ''s''₁, ''s''₂ and ''s''₃ on the right-hand side, called signs, may equal ±1, and specify whether the desired solution circle should touch the corresponding given circle internally (''s'' = 1) or externally (''s'' = −1). For example, in Figures 1 and 4, the pink solution is internally tangent to the medium-sized given circle on the right and externally tangent to the smallest and largest given circles on the left; if the given circles are ordered by radius, the signs for this solution are . Since the three signs may be chosen independently, there are eight possible sets of equations , each set corresponding to one of the eight types of solution circles.

The general system of three equations may be solved by the method of resultants. When multiplied out, all three equations have on the left-hand side, and ''r''_''s''² on the right-hand side. Subtracting one equation from another eliminates these quadratic terms; the remaining linear terms may be re-arranged to yield formulae for the coordinates ''x''_''s'' and ''y''_''s''

: $x_s = M + N r_s$

: $y_s = P + Q r_s$

where ''M'', ''N'', ''P'' and ''Q'' are known functions of the given circles and the choice of signs. Substitution of these formulae into one of the initial three equations gives a quadratic equation for ''r''_''s'', which can be solved by the quadratic formula. Substitution of the numerical value of ''r''_''s'' into the linear formulae yields the corresponding values of ''x''_''s'' and ''y''_''s''.

The signs ''s''₁, ''s''₂ and ''s''₃ on the right-hand sides of the equations may be chosen in eight possible ways, and each choice of signs gives up to two solutions, since the equation for ''r''_''s'' is quadratic. This might suggest (incorrectly) that there are up to sixteen solutions of Apollonius' problem. However, due to a symmetry of the equations, if (''r''_''s'', ''x''_''s'', ''y''_''s'') is a solution, with signs ''s''_''i'', then so is (−''r''_''s'', ''x''_''s'', ''y''_''s''), with opposite signs −''s''_''i'', which represents the same solution circle. Therefore, Apollonius' problem has at most eight independent solutions (Figure 2). One way to avoid this double-counting is to consider only solution circles with non-negative radius.

The two roots of any quadratic equation may be of three possible types: two different real numbers, two identical real numbers (i.e., a degenerate double root), or a pair of complex conjugate roots. The first case corresponds to the usual situation; each pair of roots corresponds to a pair of solutions that are related by circle inversion, as described below (Figure 6). In the second case, both roots are identical, corresponding to a solution circle that transforms into itself under inversion. In this case, one of the given circles is itself a solution to the Apollonius problem, and the number of distinct solutions is reduced by one. The third case of complex conjugate radii does not correspond to a geometrically possible solution for Apollonius' problem, since a solution circle cannot have an imaginary radius; therefore, the number of solutions is reduced by two. Apollonius' problem cannot have seven solutions, although it may have any other number of solutions from zero to eight.

Lie sphere geometry

The same algebraic equations can be derived in the context of Lie sphere geometry. That geometry represents circles, lines and points in a unified way, as a five-dimensional vector ''X'' = (''v'', ''c''_''x'', ''c''_''y'', ''w'', ''sr''), where c = (''c''_''x'', ''c''_''y'') is the center of the circle, and ''r'' is its (non-negative) radius. If ''r'' is not zero, the sign ''s'' may be positive or negative; for visualization, ''s'' represents the orientation of the circle, with counterclockwise circles having a positive ''s'' and clockwise circles having a negative ''s''. The parameter ''w'' is zero for a straight line, and one otherwise.

In this five-dimensional world, there is a bilinear product similar to the dot product:

: $\left( X_1 \mid X_2 \right) := v_1 w_2 + v_2 w_1 + \mathbf_1 \cdot \mathbf_2 - s_1 s_2 r_1 r_2.$

The Lie quadric is defined as those vectors whose product with themselves (their square norm) is zero, (''X'', ''X'') = 0. Let ''X''₁ and ''X''₂ be two vectors belonging to this quadric; the norm of their difference equals

: $\left( X_1 - X_2\mid X_1 - X_2 \right) = 2 \left( v_1 - v_2 \right) \left( w_1 - w_2 \right) + \left( \mathbf_1 - \mathbf_2 \right) \cdot \left( \mathbf_1 - \mathbf_2 \right) - \left( s_1 r_1 - s_2 r_2 \right)^2.$

The product distributes over addition and subtraction (more precisely, it is bilinear):

: $\left( X_1 - X_2 \mid X_1 - X_2 \right) = \left( X_1 \mid X_1 \right) - 2 \left( X_1 \mid X_2 \right) + \left( X_2 \mid X_2 \right).$

Since (''X''₁, ''X''₁) = (''X''₂, ''X''₂) = 0 (both belong to the Lie quadric) and since ''w''₁ = ''w''₂ = 1 for circles, the product of any two such vectors on the quadric equals

: $- 2 \left( X_1 \mid X_2 \right) = \left, \mathbf_1 - \mathbf_2 \^2 - \left( s_1 r_1 - s_2 r_2 \right)^2.$

where the vertical bars sandwiching represent the length of that difference vector, i.e., the Euclidean norm. This formula shows that if two quadric vectors ''X''₁ and ''X''₂ are orthogonal (perpendicular) to one another—that is, if (''X''₁, ''X''₂)=0—then their corresponding circles are tangent. For if the two signs ''s''₁ and ''s''₂ are the same (i.e. the circles have the same "orientation"), the circles are internally tangent; the distance between their centers equals the ''difference'' in the radii

: $\left, \mathbf_ - \mathbf_ \^ = \left( r_ - r_ \right)^.$

Conversely, if the two signs ''s''₁ and ''s''₂ are different (i.e. the circles have opposite "orientations"), the circles are externally tangent; the distance between their centers equals the ''sum'' of the radii

: $\left, \mathbf_ - \mathbf_ \^ = \left( r_ + r_ \right)^.$

Therefore, Apollonius' problem can be re-stated in Lie geometry as a problem of finding perpendicular vectors on the Lie quadric; specifically, the goal is to identify solution vectors ''X''_sol that belong to the Lie quadric and are also orthogonal (perpendicular) to the vectors ''X''₁, ''X''₂ and ''X''₃ corresponding to the given circles.

: $\left( X_\mid X_ \right) = \left( X_\mid X_ \right) = \left( X_\mid X_ \right) = \left( X_\mid X_ \right) = 0$

The advantage of this re-statement is that one can exploit theorems from linear algebra on the maximum number of linearly independent, simultaneously perpendicular vectors. This gives another way to calculate the maximum number of solutions and extend the theorem to higher-dimensional spaces.

Inversive methods

A natural setting for problem of Apollonius is inversive geometry. The basic strategy of inversive methods is to transform a given Apollonius problem into another Apollonius problem that is simpler to solve; the solutions to the original problem are found from the solutions of the transformed problem by undoing the transformation. Candidate transformations must change one Apollonius problem into another; therefore, they must transform the given points, circles and lines to other points, circles and lines, and no other shapes. Circle inversion has this property and allows the center and radius of the inversion circle to be chosen judiciously. Other candidates include the Euclidean plane isometries; however, they do not simplify the problem, since they merely shift, rotate, and mirror the original problem.

Inversion in a circle with center O and radius ''R'' consists of the following operation (Figure 5): every point P is mapped into a new point P' such that O, P, and P' are collinear, and the product of the distances of P and P' to the center O equal the radius ''R'' squared

: $\overline \cdot \overline = R^2.$

Thus, if P lies outside the circle, then P' lies within, and vice versa. When P is the same as O, the inversion is said to send P to infinity. (In complex analysis, "infinity" is defined in terms of the Riemann sphere.) Inversion has the useful property that lines and circles are always transformed into lines and circles, and points are always transformed into points. Circles are generally transformed into other circles under inversion; however, if a circle passes through the center of the inversion circle, it is transformed into a straight line, and vice versa. Importantly, if a circle crosses the circle of inversion at right angles (intersects perpendicularly), it is left unchanged by the inversion; it is transformed into itself.

Circle inversions correspond to a subset of Möbius transformations on the Riemann sphere. The planar Apollonius problem can be transferred to the sphere by an inverse stereographic projection; hence, solutions of the planar Apollonius problem also pertain to its counterpart on the sphere. Other inversive solutions to the planar problem are possible besides the common ones described below.

Pairs of solutions by inversion

Solutions to Apollonius's problem generally occur in pairs; for each solution circle, there is a conjugate solution circle (Figure 6). One solution circle excludes the given circles that are enclosed by its conjugate solution, and vice versa. For example, in Figure 6, one solution circle (pink, upper left) encloses two given circles (black), but excludes a third; conversely, its conjugate solution (also pink, lower right) encloses that third given circle, but excludes the other two. The two conjugate solution circles are related by inversion, by the following argument.

In general, any three distinct circles have a unique circle—the radical circle—that intersects all of them perpendicularly; the center of that circle is the radical center of the three circles. For illustration, the orange circle in Figure 6 crosses the black given circles at right angles. Inversion in the radical circle leaves the given circles unchanged, but transforms the two conjugate pink solution circles into one another. Under the same inversion, the corresponding points of tangency of the two solution circles are transformed into one another; for illustration, in Figure 6, the two blue points lying on each green line are transformed into one another. Hence, the lines connecting these conjugate tangent points are invariant under the inversion; therefore, they must pass through the center of inversion, which is the radical center (green lines intersecting at the orange dot in Figure 6).

Inversion to an annulus

If two of the three given circles do not intersect, a center of inversion can be chosen so that those two given circles become concentric. Under this inversion, the solution circles must fall within the annulus between the two concentric circles. Therefore, they belong to two one-parameter families. In the first family (Figure 7), the solutions do ''not'' enclose the inner concentric circle, but rather revolve like ball bearings in the annulus. In the second family (Figure 8), the solution circles enclose the inner concentric circle. There are generally four solutions for each family, yielding eight possible solutions, consistent with the algebraic solution.

When two of the given circles are concentric, Apollonius's problem can be solved easily using a method of Gauss. The radii of the three given circles are known, as is the distance ''d''_non from the common concentric center to the non-concentric circle (Figure 7). The solution circle can be determined from its radius ''r''_s, the angle θ, and the distances ''d''_s and ''d''_T from its center to the common concentric center and the center of the non-concentric circle, respectively. The radius and distance ''d''_s are known (Figure 7), and the distance ''d''_T = ''r''_s ± ''r''_non, depending on whether the solution circle is internally or externally tangent to the non-concentric circle. Therefore, by the law of cosines,

: $\cos \theta = \frac \equiv C_.$

Here, a new constant ''C'' has been defined for brevity, with the subscript indicating whether the solution is externally or internally tangent. A simple trigonometric rearrangement yields the four solutions

: $\theta = \pm 2 \arctan \left( \sqrt \right).$

This formula represents four solutions, corresponding to the two choices of the sign of θ, and the two choices for ''C''. The remaining four solutions can be obtained by the same method, using the substitutions for ''r''_s and ''d''_s indicated in Figure 8. Thus, all eight solutions of the general Apollonius problem can be found by this method.

Any initial two disjoint given circles can be rendered concentric as follows. The radical axis of the two given circles is constructed; choosing two arbitrary points P and Q on this radical axis, two circles can be constructed that are centered on P and Q and that intersect the two given circles orthogonally. These two constructed circles intersect each other in two points. Inversion in one such intersection point F renders the constructed circles into straight lines emanating from F and the two given circles into concentric circles, with the third given circle becoming another circle (in general). This follows because the system of circles is equivalent to a set of Apollonian circles, forming a bipolar coordinate system.

Resizing and inversion

The usefulness of inversion can be increased significantly by resizing. As noted in Viète's reconstruction, the three given circles and the solution circle can be resized in tandem while preserving their tangencies. Thus, the initial Apollonius problem is transformed into another problem that may be easier to solve. For example, the four circles can be resized so that one given circle is shrunk to a point; alternatively, two given circles can often be resized so that they are tangent to one another. Thirdly, given circles that intersect can be resized so that they become non-intersecting, after which the method for inverting to an annulus can be applied. In all such cases, the solution of the original Apollonius problem is obtained from the solution of the transformed problem by undoing the resizing and inversion.

= Shrinking one given circle to a point

=

In the first approach, the given circles are shrunk or swelled (appropriately to their tangency) until one given circle is shrunk to a point P. In that case, Apollonius' problem degenerates to the CCP limiting case, which is the problem of finding a solution circle tangent to the two remaining given circles that passes through the point P. Inversion in a circle centered on P transforms the two given circles into new circles, and the solution circle into a line. Therefore, the transformed solution is a line that is tangent to the two transformed given circles. There are four such solution lines, which may be constructed from the external and internal homothetic centers of the two circles. Re-inversion in P and undoing the resizing transforms such a solution line into the desired solution circle of the original Apollonius problem. All eight general solutions can be obtained by shrinking and swelling the circles according to the differing internal and external tangencies of each solution; however, different given circles may be shrunk to a point for different solutions.

= Resizing two given circles to tangency

=

In the second approach, the radii of the given circles are modified appropriately by an amount Δ''r'' so that two of them are tangential (touching). Their point of tangency is chosen as the center of inversion in a circle that intersects each of the two touching circles in two places. Upon inversion, the touching circles become two parallel lines: Their only point of intersection is sent to infinity under inversion, so they cannot meet. The same inversion transforms the third circle into another circle. The solution of the inverted problem must either be (1) a straight line parallel to the two given parallel lines and tangent to the transformed third given circle; or (2) a circle of constant radius that is tangent to the two given parallel lines and the transformed given circle. Re-inversion and adjusting the radii of all circles by Δ''r'' produces a solution circle tangent to the original three circles.

Gergonne's solution

Gergonne's approach is to consider the solution circles in pairs. Let a pair of solution circles be denoted as ''C''_A and ''C''_B (the pink circles in Figure 6), and let their tangent points with the three given circles be denoted as A₁, A₂, A₃, and B₁, B₂, B₃, respectively. Gergonne's solution aims to locate these six points, and thus solve for the two solution circles.

Gergonne's insight was that if a line ''L''₁ could be constructed such that A₁ and B₁ were guaranteed to fall on it, those two points could be identified as the intersection points of ''L''₁ with the given circle ''C''₁ (Figure 6). The remaining four tangent points would be located similarly, by finding lines ''L''₂ and ''L''₃ that contained A₂ and B₂, and A₃ and B₃, respectively. To construct a line such as ''L''₁, two points must be identified that lie on it; but these points need not be the tangent points. Gergonne was able to identify two other points for each of the three lines. One of the two points has already been identified: the radical center G lies on all three lines (Figure 6).

To locate a second point on the lines ''L''₁, ''L''₂ and ''L''₃, Gergonne noted a reciprocal relationship between those lines and the radical axis ''R'' of the solution circles, ''C''_A and ''C''_B. To understand this reciprocal relationship, consider the two tangent lines to the circle ''C''₁ drawn at its tangent points A₁ and B₁ with the solution circles; the intersection of these tangent lines is the pole point of ''L''₁ in ''C''₁. Since the distances from that pole point to the tangent points A₁ and B₁ are equal, this pole point must also lie on the radical axis ''R'' of the solution circles, by definition (Figure 9). The relationship between pole points and their polar lines is reciprocal; if the pole of ''L''₁ in ''C''₁ lies on ''R'', the pole of ''R'' in ''C''₁ must conversely lie on ''L''₁. Thus, if we can construct ''R'', we can find its pole P₁ in ''C''₁, giving the needed second point on ''L''₁ (Figure 10).

Gergonne found the radical axis ''R'' of the unknown solution circles as follows. Any pair of circles has two centers of similarity; these two points are the two possible intersections of two tangent lines to the two circles. Therefore, the three given circles have six centers of similarity, two for each distinct pair of given circles. Remarkably, these six points lie on four lines, three points on each line; moreover, each line corresponds to the radical axis of a potential pair of solution circles. To show this, Gergonne considered lines through corresponding points of tangency on two of the given circles, e.g., the line defined by A₁/A₂ and the line defined by B₁/B₂. Let X₃ be a center of similitude for the two circles ''C''₁ and ''C''₂; then, A₁/A₂ and B₁/B₂ are pairs of antihomologous points, and their lines intersect at X₃. It follows, therefore, that the products of distances are equal

: $\overline \cdot \overline = \overline \cdot \overline$

which implies that X₃ lies on the radical axis of the two solution circles. The same argument can be applied to the other pairs of circles, so that three centers of similitude for the given three circles must lie on the radical axes of pairs of solution circles.

In summary, the desired line ''L''₁ is defined by two points: the radical center G of the three given circles and the pole in ''C''₁ of one of the four lines connecting the homothetic centers. Finding the same pole in ''C''₂ and ''C''₃ gives ''L''₂ and ''L''₃, respectively; thus, all six points can be located, from which one pair of solution circles can be found. Repeating this procedure for the remaining three homothetic-center lines yields six more solutions, giving eight solutions in all. However, if a line ''L''_''k'' does not intersect its circle ''C''_''k'' for some ''k'', there is no pair of solutions for that homothetic-center line.

Intersection theory

The techniques of modern algebraic geometry, and in particular intersection theory, can be used to solve Apollonius's problem. In this approach, the problem is reinterpreted as a statement about circles in the complex projective plane. Solutions involving complex numbers are allowed and degenerate situations are counted with multiplicity. When this is done, there are always eight solutions to the problem.Eisenbud, David and Harris, Joe, ''3264 and All That: A Second Course in Algebraic Geometry''. Cambridge University Press, 2016. . pp. 66–68.

Every quadratic equation in , , and determines a unique conic, its vanishing locus. Conversely, every conic in the complex projective plane has an equation, and that equation is unique up to an overall scaling factor (because rescaling an equation does not change its vanishing locus). Therefore, the set of all conics may be parametrized by five-dimensional projective space , where the correspondence is

: \ \leftrightarrow :B:C:D:E:F\in \mathbf^5.

A ''circle'' in the complex projective plane is defined to be a conic that passes through the two points and , where denotes a square root of . The points and are called the ''circular points''. The projective variety of all circles is the subvariety of consisting of those points which correspond to conics passing through the circular points. Substituting the circular points into the equation for a generic conic yields the two equations

:$A + Bi - C = 0,$
:$A - Bi - C = 0.$

Taking the sum and difference of these equations shows that it is equivalent to impose the conditions
:$A = C$ and $B = 0$.
Therefore, the variety of all circles is a three-dimensional linear subspace of . After rescaling and completing the square, these equations also demonstrate that every conic passing through the circular points has an equation of the form

:$(X - aZ)^2 + (Y - bZ)^2 = r^2Z^2,$

which is the homogenization of the usual equation of a circle in the affine plane. Therefore, studying circles in the above sense is nearly equivalent to studying circles in the conventional sense. The only difference is that the above sense permits degenerate circles which are the union of two lines. The non-degenerate circles are called ''smooth circles'', while the degenerate ones are called '' singular circles.'' There are two types of singular circles. One is the union of the line at infinity with another line in the projective plane (possibly the line at infinity again), and the other is union of two lines in the projective plane, one through each of the two circular points. These are the limits of smooth circles as the radius tends to and , respectively. In the latter case, no point on either of the two lines has real coordinates except for the origin .

Let be a fixed smooth circle. If is any other circle, then, by the definition of a circle, and intersect at the circular points and . Because and are conics, Bézout's theorem implies and intersect in four points total, when those points are counted with the proper intersection multiplicity. That is, there are four points of intersection , , , and , but some of these points might collide. Appolonius' problem is concerned with the situation where , meaning that the intersection multiplicity at that point is ; if is also equal to a circular point, this should be interpreted as the intersection multiplicity being .

Let be the variety of circles tangent to . This variety is a quadric cone in the of all circles. To see this, consider the incidence correspondence

:$\Phi = \.$

For a curve that is the vanishing locus of a single equation , the condition that the curve meets at with multiplicity means that the Taylor series expansion of vanishes to order at ; it is therefore linear conditions on the coefficients of . This shows that, for each , the fiber of over is a cut out by two linear equations in the space of circles. Consequently, is irreducible of dimension . Since it is possible to exhibit a circle that is tangent to at only a single point, a generic element of must be tangent at only a single point. Therefore, the projection sending to is a birational morphism. It follows that the image of , which is , is also irreducible and two dimensional.

To determine the shape of , fix two distinct circles and , not necessarily tangent to . These two circles determine a pencil, meaning a line in the of circles. If the equations of and are and , respectively, then the points on correspond to the circles whose equations are , where is a point of . The points where meets are precisely the circles in the pencil that are tangent to .

There are two possibilities for the number of points of intersections. One is that either or , say , is the equation for . In this case, is a line through . If is tangent to , then so is every circle in the pencil, and therefore is contained in . The other possibility is that neither nor is the equation for . In this case, the function is a quotient of quadratics, neither of which vanishes identically. Therefore, it vanishes at two points and has poles at two points. These are the points in and , respectively, counted with multiplicity and with the circular points deducted. The rational function determines a morphism of degree two. The fiber over is the set of points for which . These are precisely the points at which the circle whose equation is meets . The branch points of this morphism are the circles tangent to . By the Riemann–Hurwitz formula, there are precisely two branch points, and therefore meets in two points. Together, these two possibilities for the intersection of and demonstrate that is a quadric cone. All such cones in are the same up to a change of coordinates, so this completely determines the shape of .

To conclude the argument, let , , and be three circles. If the intersection is finite, then it has degree , and therefore there are eight solutions to the problem of Apollonius, counted with multiplicity. To prove that the intersection is generically finite, consider the incidence correspondence

:$\Psi = \.$

There is a morphism which projects onto its final factor of . The fiber over is . This has dimension , so has dimension . Because also has dimension , the generic fiber of the projection from to the first three factors cannot have positive dimension. This proves that generically, there are eight solutions counted with multiplicity. Since it is possible to exhibit a configuration where the eight solutions are distinct, the generic configuration must have all eight solutions distinct.

Radii

In the generic problem with eight solution circles, The reciprocals of the radii of four of the solution circles sum to the same value as do the reciprocals of the radii of the other four solution circles

Special cases

Ten combinations of points, circles, and lines

Apollonius problem is to construct one or more circles tangent to three given objects in a plane, which may be circles, points, or lines. This gives rise to ten types of Apollonius' problem, one corresponding to each combination of circles, lines and points, which may be labeled with three letters, either C, L, or P, to denote whether the given elements are a circle, line or point, respectively ( Table 1). As an example, the type of Apollonius problem with a given circle, line, and point is denoted as CLP.

Some of these special cases are much easier to solve than the general case of three given circles. The two simplest cases are the problems of drawing a circle through three given points (PPP) or tangent to three lines (LLL), which were solved first by Euclid in his ''Elements''. For example, the PPP problem can be solved as follows. The center of the solution circle is equally distant from all three points, and therefore must lie on the perpendicular bisector line of any two. Hence, the center is the point of intersection of any two perpendicular bisectors. Similarly, in the LLL case, the center must lie on a line bisecting the angle at the three intersection points between the three given lines; hence, the center lies at the intersection point of two such angle bisectors. Since there are two such bisectors at every intersection point of the three given lines, there are four solutions to the general LLL problem.

Points and lines may be viewed as special cases of circles; a point can be considered as a circle of infinitely small radius, and a line may be thought of an infinitely large circle whose center is also at infinity. From this perspective, the general Apollonius problem is that of constructing circles tangent to three given circles. The nine other cases involving points and lines may be viewed as limiting cases of the general problem.

These limiting cases often have fewer solutions than the general problem; for example, the replacement of a given circle by a given point halves the number of solutions, since a point can be construed as an infinitesimal circle that is either internally or externally tangent.

Number of solutions

The problem of counting the number of solutions to different types of Apollonius' problem belongs to the field of enumerative geometry. The general number of solutions for each of the ten types of Apollonius' problem is given in Table 1 above. However, special arrangements of the given elements may change the number of solutions. For illustration, Apollonius' problem has no solution if one circle separates the two (Figure 11); to touch both the solid given circles, the solution circle would have to cross the dashed given circle; but that it cannot do, if it is to touch the dashed circle tangentially. Conversely, if three given circles are all tangent at the same point, then ''any'' circle tangent at the same point is a solution; such Apollonius problems have an infinite number of solutions. If any of the given circles are identical, there is likewise an infinity of solutions. If only two given circles are identical, there are only two distinct given circles; the centers of the solution circles form a hyperbola, as used in one solution to Apollonius' problem.

An exhaustive enumeration of the number of solutions for all possible configurations of three given circles, points or lines was first undertaken by Muirhead in 1896, although earlier work had been done by Stoll and Study. However, Muirhead's work was incomplete; it was extended in 1974 and a definitive enumeration, with 33 distinct cases, was published in 1983. Although solutions to Apollonius' problem generally occur in pairs related by inversion, an odd number of solutions is possible in some cases, e.g., the single solution for PPP, or when one or three of the given circles are themselves solutions. (An example of the latter is given in the section on Descartes' theorem.) However, there are no Apollonius problems with seven solutions. Alternative solutions based on the geometry of circles and spheres have been developed and used in higher dimensions.

Mutually tangent given circles: Soddy's circles and Descartes' theorem

If the three given circles are mutually tangent, Apollonius' problem has five solutions. Three solutions are the given circles themselves, since each is tangent to itself and to the other two given circles. The remaining two solutions (shown in red in Figure 12) correspond to the inscribed and circumscribed circles, and are called ''Soddy's circles''. This special case of Apollonius' problem is also known as the four coins problem. The three given circles of this Apollonius problem form a Steiner chain tangent to the two Soddy's circles.

Either Soddy circle, when taken together with the three given circles, produces a set of four circles that are mutually tangent at six points. The radii of these four circles are related by an equation known as Descartes' theorem. In a 1643 letter to Princess Elizabeth of Bohemia, René Descartes showed that

: $(k_1+k_2+k_3+k_s)^2 = 2( k_1^2 + k_2^2 + k_3^2 + k_s^2)$

where ''k''_''s'' = 1/''r''_''s'' and ''r''_''s'' are the curvature and radius of the solution circle, respectively, and similarly for the curvatures ''k''₁, ''k''₂ and ''k''₃ and radii ''r''₁, ''r''₂ and ''r''₃ of the three given circles. For every set of four mutually tangent circles, there is a second set of four mutually tangent circles that are tangent at the same six points.

Descartes' theorem was rediscovered independently in 1826 by Jakob Steiner, in 1842 by Philip Beecroft,

MathWords online article
) and again in 1936 by Frederick Soddy. Soddy published his findings in the scientific journal ''Nature'' as a poem, ''The Kiss Precise'', of which the first two stanzas are reproduced below. The first stanza describes Soddy's circles, whereas the second stanza gives Descartes' theorem. In Soddy's poem, two circles are said to "kiss" if they are tangent, whereas the term "bend" refers to the curvature ''k'' of the circle.

:: ''For pairs of lips to kiss maybe''
:: ''Involves no trigonometry.''
:: Tis not so when four circles kiss''
:: ''Each one the other three.''
:: ''To bring this off the four must be''
:: ''As three in one or one in three.''
:: ''If one in three, beyond a doubt''
:: ''Each gets three kisses from without.''
:: ''If three in one, then is that one''
:: ''Thrice kissed internally.''

: ''Four circles to the kissing come.''
: ''The smaller are the benter.''
: ''The bend is just the inverse of''
: ''The distance from the center.''
: ''Though their intrigue left Euclid dumb''
: ''There's now no need for rule of thumb.''
: ''Since zero bend's a dead straight line''
: ''And concave bends have minus sign,''
: ''The sum of the squares of all four bends''
: ''Is half the square of their sum.''

Sundry extensions of Descartes' theorem have been derived by Daniel Pedoe.

Generalizations

Apollonius' problem can be extended to construct all the circles that intersect three given circles at a precise angle θ, or at three specified crossing angles θ₁, θ₂ and θ₃; the ordinary Apollonius' problem corresponds to a special case in which the crossing angle is zero for all three given circles. Another generalization is the dual of the first extension, namely, to construct circles with three specified tangential distances from the three given circles.

Apollonius' problem can be extended from the plane to the sphere and other quadratic surfaces. For the sphere, the problem is to construct all the circles (the boundaries of spherical caps) that are tangent to three given circles on the sphere. This spherical problem can be rendered into a corresponding planar problem using stereographic projection. Once the solutions to the planar problem have been constructed, the corresponding solutions to the spherical problem can be determined by inverting the stereographic projection. Even more generally, one can consider the problem of four tangent curves that result from the intersections of an arbitrary quadratic surface and four planes, a problem first considered by Charles Dupin.

By solving Apollonius' problem repeatedly to find the inscribed circle, the interstices between mutually tangential circles can be filled arbitrarily finely, forming an Apollonian gasket, also known as a ''Leibniz packing'' or an ''Apollonian packing''. This gasket is a fractal, being self-similar and having a dimension ''d'' that is not known exactly but is roughly 1.3,

which is higher than that of a regular (or rectifiable) curve (''d'' = 1) but less than that of a plane (''d'' = 2). The Apollonian gasket was first described by Gottfried Leibniz in the 17th century, and is a curved precursor of the 20th-century Sierpiński triangle. The Apollonian gasket also has deep connections to other fields of mathematics; for example, it is the limit set of Kleinian groups.

The configuration of a circle tangent to ''four'' circles in the plane has special properties, which have been elucidated by Larmor (1891) and Lachlan (1893). Such a configuration is also the basis for Casey's theorem, itself a generalization of Ptolemy's theorem.

The extension of Apollonius' problem to three dimensions, namely, the problem of finding a fifth sphere that is tangent to four given spheres, can be solved by analogous methods. For example, the given and solution spheres can be resized so that one given sphere is shrunk to point while maintaining tangency. Inversion in this point reduces Apollonius' problem to finding a plane that is tangent to three given spheres. There are in general eight such planes, which become the solutions to the original problem by reversing the inversion and the resizing. This problem was first considered by Pierre de Fermat, and many alternative solution methods have been developed over the centuries. Reprinted in Euler's ''Opera Omnia'', series 1, volume 26, pp. 334–343.

Apollonius' problem can even be extended to ''d'' dimensions, to construct the hyperspheres tangent to a given set of hyperspheres. Following the publication of Frederick Soddy's re-derivation of the Descartes theorem in 1936, several people solved (independently) the mutually tangent case corresponding to Soddy's circles in ''d'' dimensions.

Applications

The principal application of Apollonius' problem, as formulated by Isaac Newton, is hyperbolic trilateration, which seeks to determine a position from the ''differences'' in distances to at least three points. For example, a ship may seek to determine its position from the differences in arrival times of signals from three synchronized transmitters. Solutions to Apollonius' problem were used in World War I to determine the location of an artillery piece from the time a gunshot was heard at three different positions, and hyperbolic trilateration is the principle used by the Decca Navigator System and LORAN. Similarly, the location of an aircraft may be determined from the difference in arrival times of its transponder signal at four receiving stations. This multilateration problem is equivalent to the three-dimensional generalization of Apollonius' problem and applies to global navigation satellite systems (see GPS#Geometric interpretation). It is also used to determine the position of calling animals (such as birds and whales), although Apollonius' problem does not pertain if the speed of sound varies with direction (i.e., the transmission medium not isotropic).

Apollonius' problem has other applications. In Book 1, Proposition 21 in his '' Principia'', Isaac Newton used his solution of Apollonius' problem to construct an orbit in celestial mechanics from the center of attraction and observations of tangent lines to the orbit corresponding to instantaneous velocity. The special case of the problem of Apollonius when all three circles are tangent is used in the Hardy–Littlewood circle method of analytic number theory to construct Hans Rademacher's contour for complex integration, given by the boundaries of an infinite set of Ford circles each of which touches several others. Finally, Apollonius' problem has been applied to some types of packing problems, which arise in disparate fields such as the error-correcting codes used on DVDs and the design of pharmaceuticals that bind in a particular enzyme of a pathogenic bacterium.

See also

* Apollonius point
* Apollonius' theorem
* Isodynamic point of a triangle

References

Further reading

*
*
*
*
* Trans., introd., and notes by Paul Ver Eecke.
*
*

External links

*
*
*
*
*

{{DEFAULTSORT:Problem Of Apollonius
Conformal geometry
Euclidean plane geometry
Incidence geometry
History of geometry