A simulation is an imitative representation of a process or system that could exist in the real world.
In this broad sense, simulation can often be used interchangeably with
model
A model is an informative representation of an object, person, or system. The term originally denoted the plans of a building in late 16th-century English, and derived via French and Italian ultimately from Latin , .
Models can be divided in ...
.
Sometimes a clear distinction between the two terms is made, in which simulations require the use of models; the model represents the key characteristics or behaviors of the selected system or process, whereas the simulation represents the evolution of the model over time.
Another way to distinguish between the terms is to define simulation as
experiment
An experiment is a procedure carried out to support or refute a hypothesis, or determine the efficacy or likelihood of something previously untried. Experiments provide insight into cause-and-effect by demonstrating what outcome occurs whe ...
ation with the help of a model. This definition includes time-independent simulations. Often,
computers are used to execute the simulation.
Simulation is used in many contexts, such as simulation of technology for
performance tuning
Performance tuning is the improvement of system Computer performance, performance. Typically in computer systems, the motivation for such activity is called a performance problem, which can be either real or anticipated. Most systems will respond t ...
or optimizing,
safety engineering
Safety engineering is an engineering Branches of science, discipline which assures that engineered systems provide acceptable levels of safety. It is strongly related to industrial engineering/systems engineering, and the subset system safety en ...
, testing, training, education, and video games. Simulation is also used with
scientific modelling
Scientific modelling is an activity that produces models representing empirical objects, phenomena, and physical processes, to make a particular part or feature of the world easier to understand, define, quantify, visualize, or simulate. It ...
of natural systems or human systems to gain insight into their functioning, as in economics. Simulation can be used to show the eventual real effects of alternative conditions and courses of action. Simulation is also used when the real system cannot be engaged, because it may not be accessible, or it may be dangerous or unacceptable to engage, or it is being designed but not yet built, or it may simply not exist.
Key issues in
modeling and simulation
Modeling and simulation (M&S) is the use of models (e.g., physical, mathematical, behavioral, or logical representation of a system, entity, phenomenon, or process) as a basis for simulations to develop data utilized for managerial or technica ...
include the acquisition of valid sources of information about the relevant selection of key characteristics and behaviors used to build the model, the use of simplifying approximations and assumptions within the model, and fidelity and validity of the simulation outcomes. Procedures and protocols for
model verification and validation are an ongoing field of academic study, refinement, research and development in simulations technology or practice, particularly in the work of computer simulation.
Classification and terminology

Historically, simulations used in different fields developed largely independently, but 20th-century studies of
systems theory
Systems theory is the Transdisciplinarity, transdisciplinary study of systems, i.e. cohesive groups of interrelated, interdependent components that can be natural or artificial. Every system has causal boundaries, is influenced by its context, de ...
and
cybernetics
Cybernetics is the transdisciplinary study of circular causal processes such as feedback and recursion, where the effects of a system's actions (its outputs) return as inputs to that system, influencing subsequent action. It is concerned with ...
combined with spreading use of computers across all those fields have led to some unification and a more systematic view of the concept.
''
Physical simulation
A simulation is an imitative representation of a process or system that could exist in the real world. In this broad sense, simulation can often be used interchangeably with model. Sometimes a clear distinction between the two terms is made, in ...
'' refers to simulation in which physical objects are substituted for the real thing. These physical objects are often chosen because they are smaller or cheaper than the actual object or system. ()
Alternatively, ''physical simulation'' may refer to computer simulations considering selected laws of physics, as in
multiphysics simulation
In computational modelling, multiphysics simulation (often shortened to simply "multiphysics") is defined as the simultaneous simulation of different aspects of a physical system or systems and the interactions among them. For example, simultaneou ...
. ()
''Interactive simulation'' is a special kind of physical simulation, often referred to as a ''
human-in-the-loop
Human-in-the-loop (HITL) is used in multiple contexts. It can be defined as a model requiring human interaction. HITL is associated with modeling and simulation (M&S) in the live, virtual, and constructive taxonomy. HITL along with the related hum ...
'' simulation, in which physical simulations include human operators, such as in a
flight simulator
A flight simulator is a device that artificially re-creates aircraft flight and the environment in which it flies, for pilot training, design, or other purposes. It includes replicating the equations that govern how aircraft fly, how they rea ...
,
sailing simulator, or
driving simulator
Driving simulators are used for entertainment as well as in training of driver's education courses taught in educational institutions and private businesses. They are also used for research purposes in the area of human factors and medical rese ...
.
''
Continuous simulation
Continuous Simulation refers to simulation approaches where a system is modeled with the help of variables that change continuously according to a set of differential equations.
History
It is notable as one of the first uses ever put to computers, ...
'' is a simulation based on
continuous-time rather than discrete-time steps, using numerical integration of
differential equations.
[McLeod, J. (1968) "Simulation: the Dynamic Modeling of Ideas And Systems with Computers", McGraw-Hill, NYC.]
''
Discrete-event simulation
A discrete-event simulation (DES) models the operation of a system as a ( discrete) sequence of events in time. Each event occurs at a particular instant in time and marks a change of state in the system. Between consecutive events, no change in t ...
'' studies systems whose states change their values only at discrete times. For example, a simulation of an epidemic could change the number of infected people at time instants when susceptible individuals get infected or when infected individuals recover.
''
Stochastic simulation A stochastic simulation is a simulation of a system that has variables that can change stochastically (randomly) with individual probabilities.DLOUHÝ, M.; FÁBRY, J.; KUNCOVÁ, M.. Simulace pro ekonomy. Praha : VŠE, 2005.
Realizations of these ...
'' is a simulation where some variable or process is subject to random variations and is projected using
Monte Carlo
Monte Carlo ( ; ; or colloquially ; , ; ) is an official administrative area of Monaco, specifically the Ward (country subdivision), ward of Monte Carlo/Spélugues, where the Monte Carlo Casino is located. Informally, the name also refers to ...
techniques using pseudo-random numbers. Thus replicated runs with the same boundary conditions will each produce different results within a specific confidence band.
''
Deterministic simulation
Determinism is the metaphysical view that all events within the universe (or multiverse) can occur only in one possible way. Deterministic theories throughout the history of philosophy have developed from diverse and sometimes overlapping mo ...
'' is a simulation which is not stochastic: thus the variables are regulated by deterministic algorithms. So replicated runs from the same boundary conditions always produce identical results.
''Hybrid simulation'' (or combined simulation) corresponds to a mix between continuous and discrete event simulation and results in integrating numerically the differential equations between two sequential events to reduce the number of discontinuities.
A ''stand-alone simulation'' is a simulation running on a single workstation by itself.
A is one which uses more than one computer simultaneously, to guarantee access from/to different resources (e.g. multi-users operating different systems, or distributed data sets); a classical example is
Distributed Interactive Simulation
Distributed Interactive Simulation (DIS) is an IEEE standard for conducting real-time platform-level wargaming across multiple host computers and is used worldwide, especially by military organizations but also by other agencies such as those inv ...
(DIS).
''Parallel simulation'' speeds up a simulation's execution by concurrently distributing its workload over multiple processors, as in
high-performance computing
High-performance computing (HPC) is the use of supercomputers and computer clusters to solve advanced computation problems.
Overview
HPC integrates systems administration (including network and security knowledge) and parallel programming into ...
.
''Interoperable simulation'' is where multiple models, simulators (often defined as federates) interoperate locally, distributed over a network; a classical example is
High-Level Architecture
The High Level Architecture (HLA) is a standard for distributed simulation, used when building a simulation for a larger purpose by combining (federating) several simulations. The standard was developed in the 1990s under the leadership of the US ...
.
''Modeling and simulation as a service'' is where simulation is accessed as a service over the web.
''Modeling, interoperable simulation and serious games'' is where
serious game
A serious game or applied game is a game designed for a primary purpose other than pure entertainment. The "serious" adjective is generally prepended to refer to video games used by industries like defense, education, scientific exploration, he ...
approaches (e.g. game engines and engagement methods) are integrated with interoperable simulation.
''Simulation fidelity'' is used to describe the accuracy of a simulation and how closely it imitates the real-life counterpart. Fidelity is broadly classified as one of three categories: low, medium, and high. Specific descriptions of fidelity levels are subject to interpretation, but the following generalizations can be made:
* Low – the minimum simulation required for a system to respond to accept inputs and provide outputs
* Medium – responds automatically to stimuli, with limited accuracy
* High – nearly indistinguishable or as close as possible to the real system
A ''synthetic environment'' is a computer simulation that can be included in human-in-the-loop simulations.
''Simulation in failure analysis'' refers to simulation in which we create environment/conditions to identify the cause of equipment failure. This can be the best and fastest method to identify the failure cause.
Computer simulation
A computer simulation (or "sim") is an attempt to model a real-life or hypothetical situation on a computer so that it can be studied to see how the system works. By changing variables in the simulation,
prediction
A prediction (Latin ''præ-'', "before," and ''dictum'', "something said") or forecast is a statement about a future event or about future data. Predictions are often, but not always, based upon experience or knowledge of forecasters. There ...
s may be made about the behaviour of the system. It is a tool to virtually investigate the behaviour of the system under study.
Computer simulation has become a useful part of
modeling
A model is an informative representation of an object, person, or system. The term originally denoted the Plan_(drawing), plans of a building in late 16th-century English, and derived via French language, French and Italian language, Italian ult ...
many natural systems in
physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge whi ...
,
chemistry
Chemistry is the scientific study of the properties and behavior of matter. It is a physical science within the natural sciences that studies the chemical elements that make up matter and chemical compound, compounds made of atoms, molecules a ...
and
biology
Biology is the scientific study of life and living organisms. It is a broad natural science that encompasses a wide range of fields and unifying principles that explain the structure, function, growth, History of life, origin, evolution, and ...
, and human systems in economics and
social science
Social science (often rendered in the plural as the social sciences) is one of the branches of science, devoted to the study of societies and the relationships among members within those societies. The term was formerly used to refer to the ...
(e.g.,
computational sociology
Computational sociology is a branch of sociology that uses computationally intensive methods to analyze and model social phenomena. Using computer simulations, artificial intelligence, complex statistical methods, and analytic approaches like soc ...
) as well as in engineering to gain insight into the operation of those systems. A good example of the usefulness of using computers to simulate can be found in the field of
network traffic simulation Network traffic simulation is a process used in telecommunications engineering to measure the efficiency of a communications network.
Overview
Telecommunications systems are complex real-world systems, containing many different components which in ...
. In such simulations, the
model
A model is an informative representation of an object, person, or system. The term originally denoted the plans of a building in late 16th-century English, and derived via French and Italian ultimately from Latin , .
Models can be divided in ...
behaviour will change each simulation according to the set of initial parameters assumed for the environment.
Traditionally, the formal modeling of systems has been via a
mathematical model
A mathematical model is an abstract and concrete, abstract description of a concrete system using mathematics, mathematical concepts and language of mathematics, language. The process of developing a mathematical model is termed ''mathematical m ...
, which attempts to find analytical solutions enabling the prediction of the behaviour of the system from a set of parameters and initial conditions. Computer simulation is often used as an adjunct to, or substitution for, modeling systems for which simple
closed form analytic solutions are not possible. There are many different types of computer simulation, the common feature they all share is the attempt to generate a sample of representative
scenario
In the performing arts, a scenario (, ; ; from Italian , "that which is pinned to the scenery") is a synoptical collage of an event or series of actions and events. In the ''commedia dell'arte'', it was an outline of entrances, exits, and actio ...
s for a model in which a complete enumeration of all possible states would be prohibitive or impossible.
Several software packages exist for running computer-based simulation modeling (e.g.
Monte Carlo
Monte Carlo ( ; ; or colloquially ; , ; ) is an official administrative area of Monaco, specifically the Ward (country subdivision), ward of Monte Carlo/Spélugues, where the Monte Carlo Casino is located. Informally, the name also refers to ...
simulation,
stochastic Stochastic (; ) is the property of being well-described by a random probability distribution. ''Stochasticity'' and ''randomness'' are technically distinct concepts: the former refers to a modeling approach, while the latter describes phenomena; i ...
modeling, multimethod modeling) that makes all the modeling almost effortless.
Modern usage of the term "computer simulation" may encompass virtually any computer-based representation.
Computer science
In
computer science
Computer science is the study of computation, information, and automation. Computer science spans Theoretical computer science, theoretical disciplines (such as algorithms, theory of computation, and information theory) to Applied science, ...
, simulation has some specialized meanings:
Alan Turing
Alan Mathison Turing (; 23 June 1912 – 7 June 1954) was an English mathematician, computer scientist, logician, cryptanalyst, philosopher and theoretical biologist. He was highly influential in the development of theoretical computer ...
used the term ''simulation'' to refer to what happens when a
universal machine
In computer science, a universal Turing machine (UTM) is a Turing machine capable of computing any computable sequence, as described by Alan Turing in his seminal paper "On Computable Numbers, with an Application to the Entscheidungsproblem". Co ...
executes a state transition table (in modern terminology, a computer runs a program) that describes the state transitions, inputs and outputs of a subject discrete-state machine. The computer simulates the subject machine. Accordingly, in
theoretical computer science
Theoretical computer science is a subfield of computer science and mathematics that focuses on the Abstraction, abstract and mathematical foundations of computation.
It is difficult to circumscribe the theoretical areas precisely. The Associati ...
the term ''
simulation
A simulation is an imitative representation of a process or system that could exist in the real world. In this broad sense, simulation can often be used interchangeably with model. Sometimes a clear distinction between the two terms is made, in ...
'' is a relation between
state transition system
In theoretical computer science, a transition system is a concept used in the study of computation. It is used to describe the potential behavior of discrete systems. It consists of states and transitions between states, which may be labeled wi ...
s, useful in the study of
operational semantics
Operational semantics is a category of formal programming language semantics in which certain desired properties of a program, such as correctness, safety or security, are verified by constructing proofs from logical statements about its exec ...
.
Less theoretically, an interesting application of computer simulation is to simulate computers using computers. In
computer architecture, a type of simulator, typically called an ''
emulator
In computing, an emulator is Computer hardware, hardware or software that enables one computer system (called the ''host'') to behave like another computer system (called the ''guest''). An emulator typically enables the host system to run sof ...
'', is often used to execute a program that has to run on some inconvenient type of computer (for example, a newly designed computer that has not yet been built or an obsolete computer that is no longer available), or in a tightly controlled testing environment (see
Computer architecture simulator
A computer architecture simulator is a program that simulates the execution of computer architecture.
Computer architecture simulators are used for the following purposes:
* Lowering cost by evaluating hardware designs without building physical ...
and
Platform virtualization
In computing, virtualization (abbreviated v12n) is a series of technologies that allows dividing of physical computing resources into a series of Virtual machine, virtual machines, Operating system, operating systems, processes or containers.
Vir ...
). For example, simulators have been used to debug a
microprogram
In processor design, microcode serves as an intermediary layer situated between the central processing unit (CPU) hardware and the programmer-visible instruction set architecture of a computer. It consists of a set of hardware-level instructions ...
or sometimes commercial application programs, before the program is downloaded to the target machine. Since the operation of the computer is simulated, all of the information about the computer's operation is directly available to the programmer, and the speed and execution of the simulation can be varied at will.
Simulators may also be used to interpret
fault tree
Fault tree analysis (FTA) is a type of failure analysis in which an undesired state of a system is examined. This analysis method is mainly used in safety engineering and reliability engineering to understand how systems can fail, to identify the ...
s, or test
VLSI logic designs before they are constructed.
Symbolic simulation
In computer science, a simulation is a computation of the execution of some appropriately modelled state-transition system. Typically this process models the complete state of the system at individual points in a discrete linear time frame, compu ...
uses variables to stand for unknown values.
In the field of
optimization
Mathematical optimization (alternatively spelled ''optimisation'') or mathematical programming is the selection of a best element, with regard to some criteria, from some set of available alternatives. It is generally divided into two subfiel ...
, simulations of physical processes are often used in conjunction with
evolutionary computation
Evolutionary computation from computer science is a family of algorithms for global optimization inspired by biological evolution, and the subfield of artificial intelligence and soft computing studying these algorithms. In technical terms ...
to optimize control strategies.
Simulation in education and training
Simulation is extensively used for educational purposes. It is used for cases where it is prohibitively expensive or simply too dangerous to allow trainees to use the real equipment in the real world. In such situations they will spend time learning valuable lessons in a "safe" virtual environment yet living a lifelike experience (or at least it is the goal). Often the convenience is to permit mistakes during training for a safety-critical system.
Simulations in education are somewhat like training simulations. They focus on specific tasks. The term 'microworld' is used to refer to educational simulations which model some abstract concept rather than simulating a realistic object or environment, or in some cases model a real-world environment in a simplistic way so as to help a learner develop an understanding of the key concepts. Normally, a user can create some sort of construction within the microworld that will behave in a way consistent with the concepts being modeled.
Seymour Papert
Seymour Aubrey Papert (; 29 February 1928 – 31 July 2016) was a South African-born American mathematician, computer scientist, and educator, who spent most of his career teaching and researching at MIT. He was one of the pioneers of artif ...
was one of the first to advocate the value of microworlds, and the
Logo
A logo (abbreviation of logotype; ) is a graphic mark, emblem, or symbol used to aid and promote public identification and recognition. It may be of an abstract or figurative design or include the text of the name that it represents, as in ...
programming environment developed by Papert is one of the most well-known microworlds.
Project management simulation is increasingly used to train students and professionals in the art and science of project management. Using simulation for
project management
Project management is the process of supervising the work of a Project team, team to achieve all project goals within the given constraints. This information is usually described in project initiation documentation, project documentation, crea ...
training improves learning retention and enhances the learning process.
''Social simulations'' may be used in social science classrooms to illustrate social and political processes in anthropology, economics, history, political science, or sociology courses, typically at the high school or university level. These may, for example, take the form of civics simulations, in which participants assume roles in a simulated society, or international relations simulations in which participants engage in negotiations, alliance formation, trade, diplomacy, and the use of force. Such simulations might be based on fictitious political systems, or be based on current or historical events. An example of the latter would be
Barnard College
Barnard College is a Private college, private Women's colleges in the United States, women's Liberal arts colleges in the United States, liberal arts college affiliated with Columbia University in New York City. It was founded in 1889 by a grou ...
's ''Reacting to the Past'' series of historical educational games. The
National Science Foundation
The U.S. National Science Foundation (NSF) is an Independent agencies of the United States government#Examples of independent agencies, independent agency of the Federal government of the United States, United States federal government that su ...
has also supported the creation of
reacting games
Reacting games are educational role-playing games set in the past, with a focus on student debates about great texts.
History
Reacting games developed as a genre of experiential education games in the United States in the late 1990s from work ...
that address science and math education. In social media simulations, participants train communication with critics and other stakeholders in a private environment.
In recent years, there has been increasing use of social simulations for staff training in aid and development agencies. The Carana simulation, for example, was first developed by the
United Nations Development Programme
The United Nations Development Programme (UNDP) is a United Nations agency tasked with helping countries eliminate poverty and achieve sustainable economic growth and human development. The UNDP emphasizes on developing local capacity towar ...
, and is now used in a very revised form by the
World Bank
The World Bank is an international financial institution that provides loans and Grant (money), grants to the governments of Least developed countries, low- and Developing country, middle-income countries for the purposes of economic development ...
for training staff to deal with fragile and conflict-affected countries.
Military uses for simulation often involve aircraft or armoured fighting vehicles, but can also target small arms and other weapon systems training. Specifically, virtual firearms ranges have become the norm in most military training processes and there is a significant amount of data to suggest this is a useful tool for armed professionals.
Virtual simulation
A virtual simulation is a category of simulation that uses simulation equipment to create a simulated world for the user. Virtual simulations allow users to interact with a
virtual world
A virtual world (also called a virtual space or spaces) is a Computer simulation, computer-simulated environment which may be populated by many simultaneous users who can create a personal Avatar (computing), avatar and independently explore th ...
. Virtual worlds operate on platforms of integrated software and hardware components. In this manner, the system can accept input from the user (e.g., body tracking, voice/sound recognition, physical controllers) and produce output to the user (e.g., visual display, aural display, haptic display) .
Virtual simulations use the aforementioned modes of interaction to produce a sense of
immersion
Immersion may refer to:
The arts
* "Immersion", a 2012 story by Aliette de Bodard
* ''Immersion'', a French comic book series by Léo Quievreux
* ''Immersion'' (album), the third album by Australian group Pendulum
* ''Immersion'' (film), a 2021 ...
for the user.
Virtual simulation input hardware

There is a wide variety of input hardware available to accept user input for virtual simulations. The following list briefly describes several of them:
* ''Body tracking'': The
motion capture
Motion capture (sometimes referred as mocap or mo-cap, for short) is the process of recording high-resolution motion (physics), movement of objects or people into a computer system. It is used in Military science, military, entertainment, sports ...
method is often used to record the user's movements and translate the captured data into inputs for the virtual simulation. For example, if a user physically turns their head, the motion would be captured by the simulation hardware in some way and translated to a corresponding shift in view within the simulation.
**
Capture suits and/or gloves may be used to capture movements of users body parts. The systems may have sensors incorporated inside them to sense movements of different body parts (e.g., fingers). Alternatively, these systems may have exterior tracking devices or marks that can be detected by external ultrasound, optical receivers or electromagnetic sensors. Internal inertial sensors are also available on some systems. The units may transmit data either wirelessly or through cables.
**
Eye tracker
Eye tracking is the process of measuring either the point of gaze (where one is looking) or the motion of an eye relative to the head. An eye tracker is a device for measuring eye positions and eye movement. Eye trackers are used in research ...
s can also be used to detect eye movements so that the system can determine precisely where a user is looking at any given instant.
* ''Physical controllers'': Physical controllers provide input to the simulation only through direct manipulation by the user. In virtual simulations, tactile feedback from physical controllers is highly desirable in a number of simulation environments.
**
Omnidirectional treadmill
An omnidirectional treadmill (ODT) is a mechanical device, similar to a typical treadmill, that allows a person to perform locomotive motion in any direction, allowing for 360 degrees of movement. The ability to move in any direction is how thes ...
s can be used to capture the users locomotion as they walk or run.
** High fidelity instrumentation such as instrument panels in virtual aircraft cockpits provides users with actual controls to raise the level of immersion. For example, pilots can use the actual
global positioning system
The Global Positioning System (GPS) is a satellite-based hyperbolic navigation system owned by the United States Space Force and operated by Mission Delta 31. It is one of the global navigation satellite systems (GNSS) that provide ge ...
controls from the real device in a simulated cockpit to help them practice procedures with the actual device in the context of the integrated cockpit system.
* ''Voice/sound recognition'': This form of interaction may be used either to interact with agents within the simulation (e.g., virtual people) or to manipulate objects in the simulation (e.g., information). Voice interaction presumably increases the level of immersion for the user.
** Users may use headsets with boom microphones, lapel microphones or the room may be equipped with strategically located microphones.
Current research into user input systems
Research in future input systems holds a great deal of promise for virtual simulations. Systems such as
brain–computer interface
A brain–computer interface (BCI), sometimes called a brain–machine interface (BMI), is a direct communication link between the brain's electrical activity and an external device, most commonly a computer or robotic limb. BCIs are often dire ...
s (BCIs) offer the ability to further increase the level of immersion for virtual simulation users. Lee, Keinrath, Scherer, Bischof, Pfurtscheller proved that naïve subjects could be trained to use a BCI to navigate a virtual apartment with relative ease. Using the BCI, the authors found that subjects were able to freely navigate the virtual environment with relatively minimal effort. It is possible that these types of systems will become standard input modalities in future virtual simulation systems.
Virtual simulation output hardware
There is a wide variety of output hardware available to deliver a stimulus to users in virtual simulations. The following list briefly describes several of them:
*''Visual display'': Visual displays provide the visual stimulus to the user.
** Stationary displays can vary from a conventional desktop display to 360-degree wrap-around screens to stereo three-dimensional screens. Conventional desktop displays can vary in size from . Wrap around screens is typically used in what is known as a
cave automatic virtual environment
A cave automatic virtual environment (better known by the recursive acronym CAVE) is an immersive virtual reality environment where projectors are directed to between three and six of the walls of a room-sized cube. The name is also a referen ...
(CAVE). Stereo three-dimensional screens produce three-dimensional images either with or without special glasses—depending on the design.
**
Head-mounted display
A head-mounted display (HMD) is a display device, worn on the head or as part of a helmet (see helmet-mounted display for aviation applications), that has a small display optic in front of one (monocular HMD) or each eye (binocular vision, bi ...
s (HMDs) have small displays that are mounted on headgear worn by the user. These systems are connected directly into the virtual simulation to provide the user with a more immersive experience. Weight, update rates and field of view are some of the key variables that differentiate HMDs. Naturally, heavier HMDs are undesirable as they cause fatigue over time. If the update rate is too slow, the system is unable to update the displays fast enough to correspond with a quick head turn by the user. Slower update rates tend to cause simulation sickness and disrupt the sense of immersion. Field of view or the angular extent of the world that is seen at a given moment
field of view
The field of view (FOV) is the angle, angular extent of the observable world that is visual perception, seen at any given moment. In the case of optical instruments or sensors, it is a solid angle through which a detector is sensitive to elec ...
can vary from system to system and has been found to affect the user's sense of immersion.
* ''Aural display'': Several different types of audio systems exist to help the user hear and localize sounds spatially. Special software can be used to produce 3D audio effects
3D audio
3D audio effects are a group of sound effects that manipulate the sound produced by Stereophonic sound, stereo speakers, Surround sound, surround-sound speakers, speaker-arrays, or headphones. This frequently involves the virtual placement of sou ...
to create the illusion that sound sources are placed within a defined three-dimensional space around the user.
** Stationary conventional speaker systems may be used to provide dual or multi-channel surround sound. However, external speakers are not as effective as headphones in producing 3D audio effects.
** Conventional headphones offer a portable alternative to stationary speakers. They also have the added advantages of masking real-world noise and facilitate more effective 3D audio sound effects.
* ''Haptic display'': These displays provide a sense of touch to the user (
haptic technology
Haptic technology (also kinaesthetic communication or 3D touch) is technology that can create an experience of touch by applying forces, vibrations, or motions to the user. These technologies can be used to create virtual objects in a computer s ...
). This type of output is sometimes referred to as force feedback.
** Tactile tile displays use different types of actuators such as inflatable bladders, vibrators, low-frequency sub-woofers, pin actuators and/or thermo-actuators to produce sensations for the user.
** End effector displays can respond to users inputs with resistance and force.
These systems are often used in medical applications for remote surgeries that employ robotic instruments.
* ''Vestibular display'': These displays provide a sense of motion to the user (
motion simulator
A motion simulator or motion platform is a mechanism that creates the feelings of being in a real motion environment. In a simulator, the movement is synchronised with a visual display of the outside world (OTW) scene. Motion platforms can provid ...
). They often manifest as motion bases for virtual vehicle simulation such as driving simulators or flight simulators. Motion bases are fixed in place but use actuators to move the simulator in ways that can produce the sensations pitching, yawing or rolling. The simulators can also move in such a way as to produce a sense of acceleration on all axes (e.g., the motion base can produce the sensation of falling).
Clinical healthcare simulators
Clinical healthcare simulators are increasingly being developed and deployed to teach therapeutic and diagnostic procedures as well as medical concepts and decision making to personnel in the health professions. Simulators have been developed for training procedures ranging from the basics such as
blood draw
In medicine, venipuncture or venepuncture is the process of obtaining intravenous access for the purpose of venous blood sampling (also called ''phlebotomy'') or intravenous therapy. In healthcare, this procedure is performed by medical labor ...
, to
laparoscopic
Laparoscopy () is an operation performed in the abdomen or human pelvis, pelvis using small Surgical incision, incisions (usually 0.5–1.5 cm) with the aid of a camera. The laparoscope aids diagnosis or therapeutic interventions with a few ...
surgery and trauma care. They are also important to help on prototyping new devices for biomedical engineering problems. Currently, simulators are applied to research and develop tools for new therapies, treatments and early diagnosis in medicine.
Many medical simulators involve a computer connected to a plastic simulation of the relevant anatomy. Sophisticated simulators of this type employ a life-size mannequin that responds to injected drugs and can be programmed to create simulations of life-threatening emergencies.
In other simulations, visual components of the procedure are reproduced by
computer graphics
Computer graphics deals with generating images and art with the aid of computers. Computer graphics is a core technology in digital photography, film, video games, digital art, cell phone and computer displays, and many specialized applications. ...
techniques, while touch-based components are reproduced by
haptic feedback devices combined with physical simulation routines computed in response to the user's actions. Medical simulations of this sort will often use 3D
CT or
MRI
Magnetic resonance imaging (MRI) is a medical imaging technique used in radiology to generate pictures of the anatomy and the physiological processes inside the body. MRI scanners use strong magnetic fields, magnetic field gradients, and rad ...
scans of patient data to enhance realism. Some medical simulations are developed to be widely distributed (such as web-enabled simulations and procedural simulations that can be viewed via standard web browsers) and can be interacted with using standard computer interfaces, such as the
keyboard
Keyboard may refer to:
Text input
* Keyboard, part of a typewriter
* Computer keyboard
** Keyboard layout, the software control of computer keyboards and their mapping
** Keyboard technology, computer keyboard hardware and firmware
Music
* Mus ...
and
mouse
A mouse (: mice) is a small rodent. Characteristically, mice are known to have a pointed snout, small rounded ears, a body-length scaly tail, and a high breeding rate. The best known mouse species is the common house mouse (''Mus musculus'' ...
.
Placebo
An important medical application of a simulator—although, perhaps, denoting a slightly different meaning of ''simulator''—is the use of a
placebo
A placebo ( ) can be roughly defined as a sham medical treatment. Common placebos include inert tablets (like sugar pills), inert injections (like saline), sham surgery, and other procedures.
Placebos are used in randomized clinical trials ...
drug, a formulation that simulates the active drug in trials of drug efficacy.
Improving patient safety
Patient safety is a concern in the medical industry. Patients have been known to suffer injuries and even death due to management error, and lack of using best standards of care and training. According to Building a National Agenda for Simulation-Based Medical Education (Eder-Van Hook, Jackie, 2004), "a health care provider's ability to react prudently in an unexpected situation is one of the most critical factors in creating a positive outcome in medical emergency, regardless of whether it occurs on the battlefield, freeway, or hospital emergency room." Eder-Van Hook (2004) also noted that medical errors kill up to 98,000 with an estimated cost between $37 and $50 million and $17 to $29 billion for preventable adverse events dollars per year.
Simulation is being used to study patient safety, as well as train medical professionals.
Studying patient safety and safety interventions in healthcare is challenging, because there is a lack of experimental control (i.e., patient complexity, system/process variances) to see if an intervention made a meaningful difference (Groves & Manges, 2017). An example of innovative simulation to study patient safety is from nursing research. Groves et al. (2016) used a high-fidelity simulation to examine nursing safety-oriented behaviors during times such as
change-of-shift report
In healthcare, a change-of-shift report is a meeting between healthcare providers at the change of shift in which vital information about and responsibility for the patient is provided from the off-going provider to the on-coming provider (Groves, ...
.
However, the value of simulation interventions to translating to clinical practice are is still debatable.
As Nishisaki states, "there is good evidence that simulation training improves provider and team
self-efficacy
In psychology, self-efficacy is an individual's belief in their capacity to act in the ways necessary to reach specific goals. The concept was originally proposed by the psychologist Albert Bandura in 1977.
Self-efficacy affects every area of hum ...
and competence on manikins. There is also good evidence that procedural simulation improves actual operational performance in clinical settings."
However, there is a need to have improved evidence to show that
crew resource management training through simulation.
One of the largest challenges is showing that team simulation improves team operational performance at the bedside.
Although evidence that simulation-based training actually improves patient outcome has been slow to accrue, today the ability of simulation to provide hands-on experience that translates to the operating room is no longer in doubt.
One of the largest factors that might impact the ability to have training impact the work of practitioners at the bedside is the ability to empower frontline staff (Stewart, Manges, Ward, 2015).
Another example of an attempt to improve patient safety through the use of simulations training is patient care to deliver just-in-time service or/and just-in-place. This training consists of 20 minutes of simulated training just before workers report to shift. One study found that just in time training improved the transition to the bedside. The conclusion as reported in Nishisaki (2008) work, was that the simulation training improved resident participation in real cases; but did not sacrifice the quality of service. It could be therefore hypothesized that by increasing the number of highly trained residents through the use of simulation training, that the simulation training does, in fact, increase patient safety.
History of simulation in healthcare
The first medical simulators were simple models of human patients.
Since antiquity, these representations in clay and stone were used to demonstrate clinical features of disease states and their effects on humans. Models have been found in many cultures and continents. These models have been used in some cultures (e.g., Chinese culture) as a "
diagnostic
Diagnosis (: diagnoses) is the identification of the nature and cause of a certain phenomenon. Diagnosis is used in a lot of different academic discipline, disciplines, with variations in the use of logic, analytics, and experience, to determine " ...
" instrument, allowing women to consult male physicians while maintaining social laws of modesty. Models are used today to help students learn the
anatomy
Anatomy () is the branch of morphology concerned with the study of the internal structure of organisms and their parts. Anatomy is a branch of natural science that deals with the structural organization of living things. It is an old scien ...
of the
musculoskeletal
The human musculoskeletal system (also known as the human locomotor system, and previously the activity system) is an organ system that gives humans the ability to move using their muscular and skeletal systems. The musculoskeletal system provid ...
system and organ systems.
In 2002, the
Society for Simulation in Healthcare (SSH) was formed to become a leader in international interprofessional advances the application of medical simulation in healthcare
The need for a "uniform mechanism to educate, evaluate, and certify simulation instructors for the health care profession" was recognized by McGaghie et al. in their critical review of simulation-based medical education research.
In 2012 the SSH piloted two new certifications to provide recognition to educators in an effort to meet this need.
Type of models
Active models
Active models that attempt to reproduce living anatomy or physiology are recent developments. The famous
"Harvey" mannequin was developed at the
University of Miami
The University of Miami (UM, UMiami, Miami, U of M, and The U) is a private university, private research university in Coral Gables, Florida, United States. , the university enrolled 19,852 students in two colleges and ten schools across over ...
and is able to recreate many of the physical findings of the
cardiology
Cardiology () is the study of the heart. Cardiology is a branch of medicine that deals with disorders of the heart and the cardiovascular system. The field includes medical diagnosis and treatment of congenital heart defects, coronary artery di ...
examination, including
palpation
Palpation is the process of using one's hands to check the body, especially while perceiving/diagnosing a disease or illness. Usually performed by a health care practitioner, it is the process of feeling an object in or on the body to determine ...
,
auscultation
Auscultation (based on the Latin verb ''auscultare'' "to listen") is listening to the internal sounds of the body, usually using a stethoscope. Auscultation is performed for the purposes of examining the circulatory system, circulatory and resp ...
, and
electrocardiography
Electrocardiography is the process of producing an electrocardiogram (ECG or EKG), a recording of the heart's electrical activity through repeated cardiac cycles.
It is an electrogram of the heart which is a graph of voltage versus time of t ...
.
Interactive models
More recently, interactive models have been developed that respond to actions taken by a student or physician.
[ Until recently, these simulations were two dimensional computer programs that acted more like a textbook than a patient. Computer simulations have the advantage of allowing a student to make judgments, and also to make errors. The process of iterative learning through assessment, evaluation, decision making, and error correction creates a much stronger learning environment than passive instruction.
]
Computer simulators
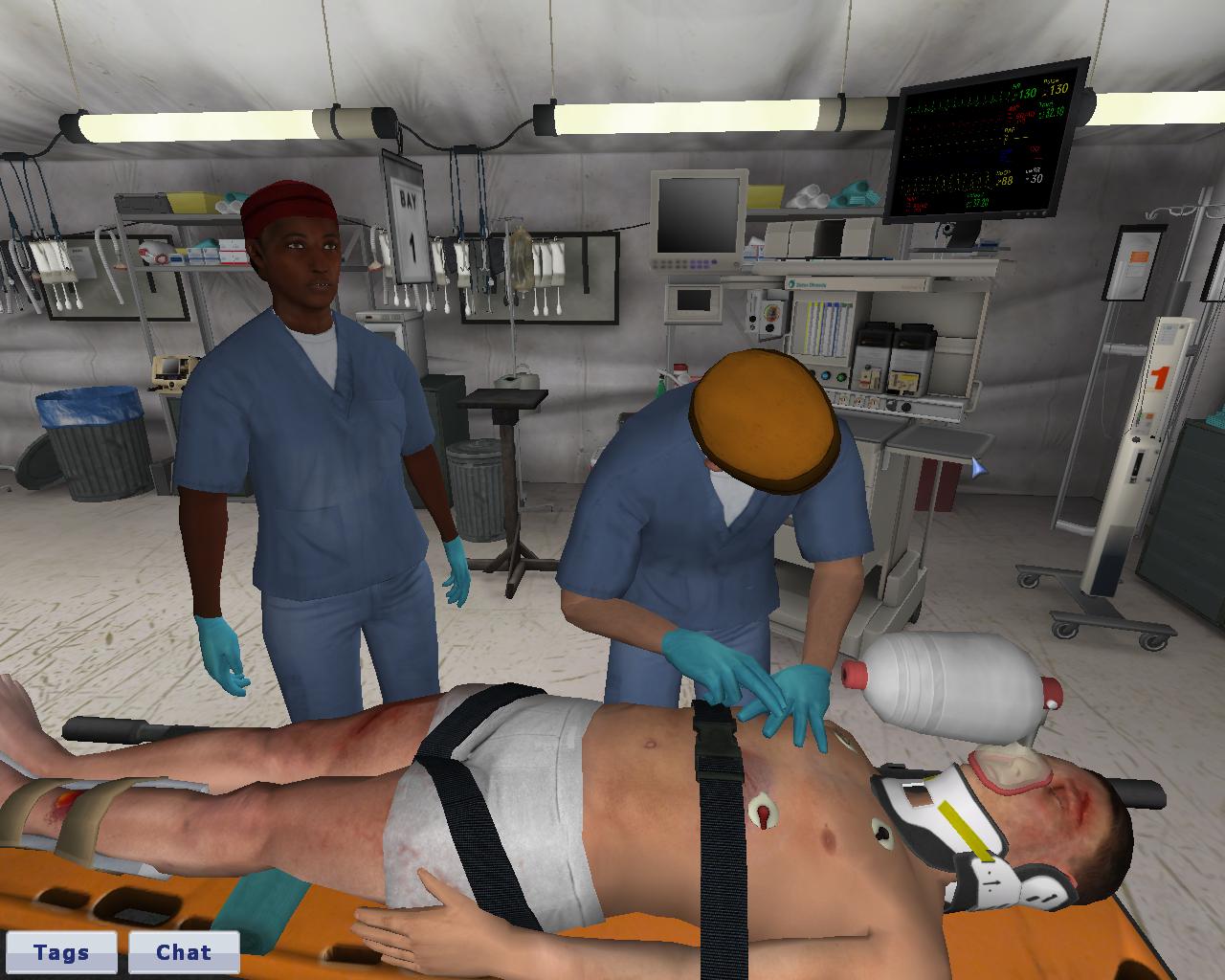 Simulators have been proposed as an ideal tool for assessment of students for clinical skills.
Simulators have been proposed as an ideal tool for assessment of students for clinical skills.
Simulation in entertainment
Simulation in entertainment encompasses many large and popular industries such as film, television, video games (including serious game
A serious game or applied game is a game designed for a primary purpose other than pure entertainment. The "serious" adjective is generally prepended to refer to video games used by industries like defense, education, scientific exploration, he ...
s) and rides in theme parks. Although modern simulation is thought to have its roots in training and the military, in the 20th century it also became a conduit for enterprises which were more hedonistic in nature.
History of visual simulation in film and games
Early history (1940s and 1950s)
The first simulation game may have been created as early as 1947 by Thomas T. Goldsmith Jr. and Estle Ray Mann. This was a straightforward game that simulated a missile being fired at a target. The curve of the missile and its speed could be adjusted using several knobs. In 1958, a computer game called ''Tennis for Two
''Tennis for Two'' (also known as ''Computer Tennis'') is a sports video game that simulates a game of tennis, and was one of the first games developed in the early history of video games. American physicist William Higinbotham designed the game ...
'' was created by Willy Higginbotham which simulated a tennis game between two players who could both play at the same time using hand controls and was displayed on an oscilloscope. This was one of the first electronic video games to use a graphical display.
1970s and early 1980s
Computer-generated imagery
Computer-generated imagery (CGI) is a specific-technology or application of computer graphics for creating or improving images in Digital art, art, Publishing, printed media, Training simulation, simulators, videos and video games. These images ...
was used in the film to simulate objects as early as 1972 in ''A Computer Animated Hand
''A Computer Animated Hand'' is the title of a 1972 American List of computer-animated films, computer-animated short film produced by Edwin Catmull and Fred Parke. Produced during Catmull's tenure at the University of Utah, the short was created ...
'', parts of which were shown on the big screen in the 1976 film ''Futureworld
''Futureworld'' is a 1976 American science fiction thriller film directed by Richard T. Heffron and written by Mayo Simon and George Schenck. It is a sequel to the 1973 Michael Crichton film '' Westworld'', and is the second installment in ...
''. This was followed by the "targeting computer" that young Skywalker turns off in the 1977 film ''Star Wars
''Star Wars'' is an American epic film, epic space opera media franchise created by George Lucas, which began with the Star Wars (film), eponymous 1977 film and Cultural impact of Star Wars, quickly became a worldwide popular culture, pop cu ...
''.
The film ''Tron
''Tron'' (stylized as ''TRON'') is a 1982 American science fiction action adventure film written and directed by Steven Lisberger from a story by Lisberger and Bonnie MacBird. The film stars Jeff Bridges as Kevin Flynn, a computer programmer ...
'' (1982) was the first film to use computer-generated imagery for more than a couple of minutes.
Advances in technology in the 1980s caused 3D simulation to become more widely used and it began to appear in movies and in computer-based games such as Atari's '' Battlezone'' (1980) and Acornsoft
Acornsoft was the software arm of Acorn Computers, and a major publisher of software for the BBC Micro and Acorn Electron. As well as games, it also produced a large number of educational titles, extra computer languages and business and util ...
's ''Elite
In political and sociological theory, the elite (, from , to select or to sort out) are a small group of powerful or wealthy people who hold a disproportionate amount of wealth, privilege, political power, or skill in a group. Defined by the ...
'' (1984), one of the first wire-frame 3D graphics games for home computer
Home computers were a class of microcomputers that entered the market in 1977 and became common during the 1980s. They were marketed to consumers as affordable and accessible computers that, for the first time, were intended for the use of a s ...
s.
Pre-virtual cinematography era (early 1980s to 1990s)
Advances in technology in the 1980s made the computer more affordable and more capable than they were in previous decades, which facilitated the rise of computer such as the Xbox gaming. The first video game console
A video game console is an electronic device that Input/output, outputs a video signal or image to display a video game that can typically be played with a game controller. These may be home video game console, home consoles, which are generally ...
s released in the 1970s and early 1980s fell prey to the industry crash in 1983, but in 1985, Nintendo
is a Japanese Multinational corporation, multinational video game company headquartered in Kyoto. It develops, publishes, and releases both video games and video game consoles.
The history of Nintendo began when craftsman Fusajiro Yamauchi ...
released the Nintendo Entertainment System (NES) which became one of the best selling consoles in video game history. In the 1990s, computer games became widely popular with the release of such game as ''The Sims
''The Sims'' is a series of life simulation video games developed by Maxis and Video game publisher, published by Electronic Arts. The franchise has sold nearly 200 million copies worldwide, and is one of the List of best-selling video game fran ...
'' and ''Command & Conquer
''Command & Conquer'' (''C&C'') is a real-time strategy (RTS) video game franchise created and originally developed by Westwood Studios and currently owned by Electronic Arts. The first game was one of the earliest of the RTS genre, itself ba ...
'' and the still increasing power of desktop computers. Today, computer simulation games such as ''World of Warcraft
''World of Warcraft'' (''WoW'') is a 2004 massively multiplayer online role-playing (MMORPG) video game developed and published by Blizzard Entertainment for Windows and Mac OS X. Set in the '' Warcraft'' fantasy universe, ''World of War ...
'' are played by millions of people around the world.
In 1993, the film ''Jurassic Park
''Jurassic Park'', later referred to as ''Jurassic World'', is an American science fiction media franchise created by Michael Crichton, centered on a disastrous attempt to create a theme park of De-extinction#Cloning, cloned dinosaurs. It bega ...
'' became the first popular film to use computer-generated graphics extensively, integrating the simulated dinosaurs almost seamlessly into live action scenes.
This event transformed the film industry; in 1995, the film ''Toy Story
''Toy Story'' is a 1995 American animated adventure comedy film produced by Pixar Animation Studios for Walt Disney Pictures. It is the first installment in the Toy Story (franchise), ''Toy Story'' franchise and the Firsts in animation, firs ...
'' was the first film to use only computer-generated images and by the new millennium computer generated graphics were the leading choice for special effects in films.
Virtual cinematography (early 2000s–present)
The advent of virtual cinematography
Virtual cinematography is the set of Cinematography, cinematographic techniques performed in a computer graphics environment. It includes a wide variety of subjects like photographing real objects, often with Stereo camera, stereo or multi-camer ...
in the early 2000s has led to an explosion of movies that would have been impossible to shoot without it. Classic examples are the digital look-alikes of Neo, Smith and other characters in the ''Matrix'' sequels and the extensive use of physically impossible camera runs in ''The Lord of the Rings'' trilogy.
The terminal in the Pan Am (TV series)
''Pan Am'' is an American period drama television series created by writer Jack Orman. Named for the iconic Pan American World Airways, the series features the aircraft pilots and stewardesses of the fictional Pan Am ''Clipper Majestic'', oper ...
no longer existed during the filming of this 2011–2012 aired series, which was no problem as they created it in virtual cinematography using automated
Automation describes a wide range of technologies that reduce human intervention in processes, mainly by predetermining decision criteria, subprocess relationships, and related actions, as well as embodying those predeterminations in machine ...
viewpoint
Viewpoint may refer to:
* Scenic viewpoint, a high place where people can gather to view scenery
In computing
* Viewpoint model, a computer science technique for making complex systems more comprehensible to human engineers
* Viewpoint Corpora ...
finding and matching in conjunction with compositing real and simulated footage, which has been the bread and butter of the movie artist in and around film studio
A film studio (also known as movie studio or simply studio) is a major entertainment company that makes films. Today, studios are mostly financing and distribution entities. In addition, they may have their own studio facility or facilities; how ...
s since the early 2000s.
Computer-generated imagery
Computer-generated imagery (CGI) is a specific-technology or application of computer graphics for creating or improving images in Digital art, art, Publishing, printed media, Training simulation, simulators, videos and video games. These images ...
is "the application of the field of 3D computer graphics to special effects". This technology is used for visual effects because they are high in quality, controllable, and can create effects that would not be feasible using any other technology either because of cost, resources or safety. Computer-generated graphics can be seen in many live-action movies today, especially those of the action genre. Further, computer-generated imagery has almost completely supplanted hand-drawn animation in children's movies which are increasingly computer-generated only. Examples of movies that use computer-generated imagery include ''Finding Nemo
''Finding Nemo'' is a 2003 American animated comedy-drama adventure film produced by Pixar Animation Studios for Walt Disney Pictures. The film was directed by Andrew Stanton, co-directed by Lee Unkrich, and produced by Graham Walters, from ...
'', ''300
__NOTOC__
Year 300 ( CCC) was a leap year starting on Monday of the Julian calendar. At the time, it was known as the Year of the Consulship of Constantius and Valerius (or, less frequently, year 1053 ''Ab urbe condita''). The denomination 300 ...
'' and ''Iron Man
Iron Man is a superhero appearing in American comic books published by Marvel Comics. Co-created by writer and editor Stan Lee, developed by scripter Larry Lieber, and designed by artists Don Heck and Jack Kirby, the character first appearan ...
''.
Examples of non-film entertainment simulation
Simulation games
Simulation games
Simulation video games are a diverse super-category of video games, generally designed to closely simulate real world activities. A simulation game attempts to copy various activities from real life in the form of a game for various purposes such ...
, as opposed to other genres of video and computer games, represent or simulate an environment accurately. Moreover, they represent the interactions between the playable characters and the environment realistically. These kinds of games are usually more complex in terms of gameplay. Simulation games have become incredibly popular among people of all ages. Popular simulation games include ''SimCity
''SimCity'' is an open-ended city-building video game franchise originally designed by Will Wright. The first game in the series, '' SimCity'', was published by Maxis in 1989 and was followed by several sequels and many other spin-off ''S ...
'' and ''Tiger Woods PGA Tour
''PGA Tour'' is a series of golf video games developed and published by Electronic Arts - and later their EA Sports sub-label - since 1990. The series primarily features courses featured on the U.S. PGA Tour, and other notable courses (such as ...
''. There are also flight simulator
A flight simulator is a device that artificially re-creates aircraft flight and the environment in which it flies, for pilot training, design, or other purposes. It includes replicating the equations that govern how aircraft fly, how they rea ...
and driving simulator
Driving simulators are used for entertainment as well as in training of driver's education courses taught in educational institutions and private businesses. They are also used for research purposes in the area of human factors and medical rese ...
games.
Theme park rides
Simulators have been used for entertainment since the Link Trainer
The term Link Trainer, also known as the "Blue box" and "Pilot Trainer" is commonly used to refer to a series of flight simulators produced between the early 1930s and early 1950s by Link Aviation Devices, founded and headed by Ed Link, based o ...
in the 1930s. The first modern simulator ride to open at a theme park was Disney's Star Tours
Star Tours was a motion simulator attraction at several Disney theme parks, based on the successful ''Star Wars'' film series created by George Lucas. Set in the ''Star Wars'' universe, the attraction sent guests on an excursion trip to ...
in 1987 soon followed by Universal's The Funtastic World of Hanna-Barbera
''The Funtastic World of Hanna-Barbera'' is an American animated syndicated programming block produced by Hanna-Barbera Productions that ran on a weekly schedule and was performed in live action. The program ran from 1985 to 1994.
Overview
The ...
in 1990 which was the first ride to be done entirely with computer graphics.[simulatr.](_blank)
/ref>
Simulator rides are the progeny of military training simulators and commercial simulators, but they are different in a fundamental way. While military training simulators react realistically to the input of the trainee in real time, ride simulators only feel like they move realistically and move according to prerecorded motion scripts.The Amazing Adventures of Spider-Man
The Amazing Adventures of Spider-Man, also known as The Amazing Adventures of Spider-Man – The Ride is a 3D motion simulator and dark ride located at Universal Islands of Adventure in Orlando, Florida. Based on the Marvel Comics superhero Spid ...
include elements to increase the amount of immersion experienced by the riders such as: 3D imagery, physical effects (spraying water or producing scents), and movement through an environment.
Simulation and manufacturing
Manufacturing simulation represents one of the most important applications of simulation. This technique represents a valuable tool used by engineers when evaluating the effect of capital investment in equipment and physical facilities like factory plants, warehouses, and distribution centers. Simulation can be used to predict the performance of an existing or planned system and to compare alternative solutions for a particular design problem.
Another important goal of simulation in manufacturing systems Simulation in manufacturing systems is the use of software to make computer models of manufacturing systems, so to analyze them and thereby obtain important information. It has been syndicated as the second most popular management science among manu ...
is to quantify system performance. Common measures of system performance include the following:
* Throughput under average and peak loads
* System cycle time (how long it takes to produce one part)
* Use of resource, labor, and machines
* Bottlenecks and choke points
* Queuing at work locations
* Queuing and delays caused by material-handling devices and systems
* WIP storages needs
* Staffing requirements
* Effectiveness of scheduling systems
* Effectiveness of control systems
More examples of simulation
Automobiles
An automobile simulator provides an opportunity to reproduce the characteristics of real vehicles in a virtual environment. It replicates the external factors and conditions with which a vehicle interacts enabling a driver to feel as if they are sitting in the cab of their own vehicle. Scenarios and events are replicated with sufficient reality to ensure that drivers become fully immersed in the experience rather than simply viewing it as an educational experience.
The simulator provides a constructive experience for the novice driver and enables more complex exercises to be undertaken by the more mature driver. For novice drivers, truck simulators provide an opportunity to begin their career by applying best practice. For mature drivers, simulation provides the ability to enhance good driving or to detect poor practice and to suggest the necessary steps for remedial action. For companies, it provides an opportunity to educate staff in the driving skills that achieve reduced maintenance costs, improved productivity and, most importantly, to ensure the safety of their actions in all possible situations.
File:Car racing simulator - SBR Racing, Construma, 2015.04.17.JPG, Car racing simulator
File:Vehicle simulator.jpg, A soldier tests out a heavy-wheeled-vehicle driving simulator.
Biomechanics
A biomechanics simulator is a simulation platform for creating dynamic mechanical models built from combinations of rigid and deformable bodies, joints, constraints, and various force actuators. It is specialized for creating biomechanical models of human anatomical structures, with the intention to study their function and eventually assist in the design and planning of medical treatment.
A biomechanics simulator is used to analyze walking dynamics, study sports performance, simulate surgical procedures, analyze joint loads, design medical devices, and animate human and animal movement.
A neuromechanical simulator that combines biomechanical and biologically realistic neural network simulation. It allows the user to test hypotheses on the neural basis of behavior in a physically accurate 3-D virtual environment.
City and urban
A city simulator can be a city-building game
A city-building game, or town-building game, is a Video game genres, genre of simulation video game where players act as the overall planner and leader of a city or town, looking down on it from above, and being responsible for its growth and man ...
but can also be a tool used by urban planners to understand how cities are likely to evolve in response to various policy decisions. AnyLogic
AnyLogic is a multimethod simulation modeling tool developed by The AnyLogic Company (formerly XJ Technologies). It supports agent-based, discrete event, and system dynamics simulation methodologies.Christopher W. Weimer,
J. O. Miller, Raymond R ...
is an example of modern, large-scale urban simulators designed for use by urban planners. City simulators are generally agent
Agent may refer to:
Espionage, investigation, and law
*, spies or intelligence officers
* Law of agency, laws involving a person authorized to act on behalf of another
** Agent of record, a person with a contractual agreement with an insuran ...
-based simulations with explicit representations for land use
Land use is an umbrella term to describe what happens on a parcel of land. It concerns the benefits derived from using the land, and also the land management actions that humans carry out there. The following categories are used for land use: fo ...
and transportation. UrbanSim
UrbanSim is an open source urban simulation system designed by Paul Waddell of the University of California, Berkeley and developed with numerous collaborators to support metropolitan land use, transportation, and environmental planning. It has ...
and LEAM are examples of large-scale urban simulation models that are used by metropolitan planning agencies and military bases for land use and transportation planning
Transportation planning is the process of defining future policies, goals, investments, and spatial planning designs to prepare for future needs to move people and goods to destinations. As practiced today, it is a collaborative process that i ...
.
Christmas
Several Christmas-themed simulations exist, many of which are centred around Santa Claus
Santa Claus (also known as Saint Nicholas, Saint Nick, Father Christmas, Kris Kringle or Santa) is a legendary figure originating in Western Christian culture who is said to bring gifts during the late evening and overnight hours on Chris ...
. An example of these simulations are websites which claim to allow the user to track Santa Claus. Due to the fact that Santa is a legend
A legend is a genre of folklore that consists of a narrative featuring human actions, believed or perceived to have taken place in human history. Narratives in this genre may demonstrate human values, and possess certain qualities that give the ...
ary character and not a real, living person, it is impossible to provide actual information on his location, and services such as NORAD Tracks Santa
NORAD Tracks Santa, also called NORAD Santa Tracker, is an annual official program in which North American Aerospace Defense Command (NORAD) publishes the tracking of Santa Claus, who leaves the North Pole to travel around the world on his missi ...
and the Google Santa Tracker
Google Santa Tracker is an annual Christmas-themed entertainment website first launched on December 1st, 2004 by Google that simulates the tracking of the legendary character Santa Claus on Christmas Eve, using predetermined location informat ...
(the former of which claims to use radar
Radar is a system that uses radio waves to determine the distance ('' ranging''), direction ( azimuth and elevation angles), and radial velocity of objects relative to the site. It is a radiodetermination method used to detect and track ...
and other technologies to track Santa) display fake, predetermined location information to users. Another example of these simulations are websites that claim to allow the user to email or send messages to Santa Claus. Websites such as emailSanta.com
emailSanta.com is a Christmas-themed entertainment website run by Alan Kerr which simulates emailing Santa Claus. It also provides various other Christmas-themed simulations. Users compose their letter by filling out a blank form, then the webs ...
or Santa's former page on the now-defunct Windows Live Spaces
Windows Live Spaces was Microsoft's blogging platform and social network service. The site was originally released in early 2004 as MSN Spaces to compete with other social networking services, and re-launched in 2006 as a part of a shifting of com ...
by Microsoft
Microsoft Corporation is an American multinational corporation and technology company, technology conglomerate headquartered in Redmond, Washington. Founded in 1975, the company became influential in the History of personal computers#The ear ...
use automated programs or scripts to generate personalized replies claimed to be from Santa himself based on user input.
Classroom of the future
The classroom of the future will probably contain several kinds of simulators, in addition to textual and visual learning tools. This will allow students to enter the clinical years better prepared, and with a higher skill level. The advanced student or postgraduate will have a more concise and comprehensive method of retraining—or of incorporating new clinical procedures into their skill set—and regulatory bodies and medical institutions will find it easier to assess the proficiency and competency of individuals.
The classroom of the future will also form the basis of a clinical skills unit for continuing education of medical personnel; and in the same way that the use of periodic flight training assists airline pilots, this technology will assist practitioners throughout their career.
The simulator will be more than a "living" textbook, it will become an integral a part of the practice of medicine. The simulator environment will also provide a standard platform for curriculum development in institutions of medical education.
Communication satellites
Modern satellite communications systems ( SATCOM) are often large and complex with many interacting parts and elements. In addition, the need for broadband connectivity on a moving vehicle has increased dramatically in the past few years for both commercial and military applications. To accurately predict and deliver high quality of service, SATCOM system designers have to factor in terrain as well as atmospheric and meteorological conditions in their planning. To deal with such complexity, system designers and operators increasingly turn towards computer models of their systems to simulate real-world operating conditions and gain insights into usability and requirements prior to final product sign-off. Modeling improves the understanding of the system by enabling the SATCOM system designer or planner to simulate real-world performance by injecting the models with multiple hypothetical atmospheric and environmental conditions. Simulation is often used in the training of civilian and military personnel. This usually occurs when it is prohibitively expensive or simply too dangerous to allow trainees to use the real equipment in the real world. In such situations, they will spend time learning valuable lessons in a "safe" virtual environment yet living a lifelike experience (or at least it is the goal). Often the convenience is to permit mistakes during training for a safety-critical system.
Digital lifecycle
Simulation solutions are being increasingly integrated with computer-aided
Automation describes a wide range of technologies that reduce human intervention in processes, mainly by predetermining decision criteria, subprocess relationships, and related actions, as well as embodying those predeterminations in machine ...
solutions and processes (computer-aided design
Computer-aided design (CAD) is the use of computers (or ) to aid in the creation, modification, analysis, or optimization of a design. This software is used to increase the productivity of the designer, improve the quality of design, improve c ...
or CAD, computer-aided manufacturing
Computer-aided manufacturing (CAM) also known as computer-aided modeling or computer-aided machining is the use of software to control machine tools in the manufacturing of work pieces. This is not the only definition for CAM, but it is the most ...
or CAM, computer-aided engineering
Computer-aided engineering (CAE) is the general usage of technology to aid in tasks related to engineering analysis. Any use of technology to solve or assist engineering issues falls under this umbrella.
Overview
Following alongside the con ...
or CAE, etc.). The use of simulation throughout the product lifecycle
In Industry (economics), industry, product lifecycle management (PLM) is the process of managing the entire lifecycle of a product from its inception through the Product engineering, engineering, Product design, design, and Manufacturing, ma ...
, especially at the earlier concept and design stages, has the potential of providing substantial benefits. These benefits range from direct cost issues such as reduced prototyping and shorter time-to-market to better performing products and higher margins. However, for some companies, simulation has not provided the expected benefits.
The successful use of simulation, early in the lifecycle, has been largely driven by increased integration of simulation tools with the entire set of CAD, CAM and product-lifecycle management solutions. Simulation solutions can now function across the extended enterprise in a multi-CAD environment, and include solutions for managing simulation data and processes and ensuring that simulation results are made part of the product lifecycle history.
Disaster preparedness
Simulation training has become a method for preparing people for disasters. Simulations can replicate emergency situations and track how learners respond thanks to a lifelike experience. Disaster preparedness simulations can involve training on how to handle terrorism
Terrorism, in its broadest sense, is the use of violence against non-combatants to achieve political or ideological aims. The term is used in this regard primarily to refer to intentional violence during peacetime or in the context of war aga ...
attacks, natural disasters, pandemic
A pandemic ( ) is an epidemic of an infectious disease that has a sudden increase in cases and spreads across a large region, for instance multiple continents or worldwide, affecting a substantial number of individuals. Widespread endemic (epi ...
outbreaks, or other life-threatening emergencies.
One organization that has used simulation training for disaster preparedness is CADE (Center for Advancement of Distance Education). CADE has used a video game to prepare emergency workers for multiple types of attacks. As reported by News-Medical.Net, "The video game is the first in a series of simulations to address bioterrorism, pandemic flu, smallpox, and other disasters that emergency personnel must prepare for." Developed by a team from the University of Illinois at Chicago
The University of Illinois Chicago (UIC) is a public research university in Chicago, Illinois, United States. Its campus is in the Near West Side community area, adjacent to the Chicago Loop. The second campus established under the Universi ...
(UIC), the game allows learners to practice their emergency skills in a safe, controlled environment.
The Emergency Simulation Program (ESP) at the British Columbia Institute of Technology (BCIT), Vancouver, British Columbia, Canada is another example of an organization that uses simulation to train for emergency situations. ESP uses simulation to train on the following situations: forest fire fighting, oil or chemical spill response, earthquake response, law enforcement, municipal firefighting, hazardous material handling, military training, and response to terrorist attack
Economics
Simulations in economics and especially in macroeconomics
Macroeconomics is a branch of economics that deals with the performance, structure, behavior, and decision-making of an economy as a whole. This includes regional, national, and global economies. Macroeconomists study topics such as output (econ ...
, judge the desirability of the effects of proposed policy actions, such as fiscal policy
In economics and political science, fiscal policy is the use of government revenue collection ( taxes or tax cuts) and expenditure to influence a country's economy. The use of government revenue expenditures to influence macroeconomic variab ...
changes or monetary policy
Monetary policy is the policy adopted by the monetary authority of a nation to affect monetary and other financial conditions to accomplish broader objectives like high employment and price stability (normally interpreted as a low and stable rat ...
changes. A mathematical model of the economy, having been fitted to historical economic data, is used as a proxy for the actual economy; proposed values of government spending
Government spending or expenditure includes all government consumption, investment, and transfer payments. In national income accounting, the acquisition by governments of goods and services for current use, to directly satisfy the individual or ...
, taxation, open market operations
In macroeconomics, an open market operation (OMO) is an activity by a central bank to exchange liquidity in its currency with a bank or a group of banks. The central bank can either transact government bonds and other financial assets in the open ...
, etc. are used as inputs to the simulation of the model, and various variables of interest such as the inflation rate
In economics, inflation is an increase in the average price of goods and services in terms of money. This increase is measured using a price index, typically a consumer price index (CPI). When the general price level rises, each unit of curre ...
, the unemployment rate
Unemployment, according to the OECD (Organisation for Economic Co-operation and Development), is the proportion of people above a specified age (usually 15) not being in paid employment or self-employment but currently available for work d ...
, the balance of trade
Balance of trade is the difference between the monetary value of a nation's exports and imports of goods over a certain time period. Sometimes, trade in Service (economics), services is also included in the balance of trade but the official IMF d ...
deficit, the government budget deficit
Within the budgetary process, deficit spending is the amount by which spending exceeds revenue over a particular period of time, also called simply deficit, or budget deficit, the opposite of budget surplus. The term may be applied to the budg ...
, etc. are the outputs of the simulation. The simulated values of these variables of interest are compared for different proposed policy inputs to determine which set of outcomes is most desirable.
Engineering, technology, and processes
Simulation is an important feature in engineering systems or any system that involves many processes. For example, in electrical engineering
Electrical engineering is an engineering discipline concerned with the study, design, and application of equipment, devices, and systems that use electricity, electronics, and electromagnetism. It emerged as an identifiable occupation in the l ...
, delay lines may be used to simulate propagation delay
Propagation delay is the time duration taken for a signal to reach its destination, for example in the electromagnetic field, a wire, speed of sound, gas, fluid or seismic wave, solid body.
Physics
* An electromagnetic wave travelling through ...
and phase shift
In physics and mathematics, the phase (symbol φ or ϕ) of a wave or other periodic function F of some real variable t (such as time) is an angle-like quantity representing the fraction of the cycle covered up to t. It is expressed in such a s ...
caused by an actual transmission line
In electrical engineering, a transmission line is a specialized cable or other structure designed to conduct electromagnetic waves in a contained manner. The term applies when the conductors are long enough that the wave nature of the transmis ...
. Similarly, dummy load
A dummy load is a device used to simulate an electrical load, usually for testing purposes. In radio a dummy antenna is connected to the output of a radio transmitter and electrically simulates an antenna, to allow the transmitter to be adjust ...
s may be used to simulate impedance without simulating propagation and is used in situations where propagation is unwanted. A simulator may imitate only a few of the operations and functions of the unit it simulates. ''Contrast with'': emulate
Emulate, Inc. (Emulate) is a biotechnology company that commercialized Organs-on-Chips technology—a human cell-based technology that recreates organ-level function to model organs in healthy and diseased states. The technology has applications ...
.Federal Standard 1037C
Federal Standard 1037C, titled Telecommunications: Glossary of Telecommunication Terms, is a United States Federal Standard issued by the General Services Administration pursuant to the Federal Property and Administrative Services Act of 1949, ...
fluid dynamics
In physics, physical chemistry and engineering, fluid dynamics is a subdiscipline of fluid mechanics that describes the flow of fluids – liquids and gases. It has several subdisciplines, including (the study of air and other gases in motion ...
problems often require both mathematical and physical simulations. In these cases the physical models require dynamic similitude
Similitude is a concept applicable to the testing of engineering models. A model is said to have ''similitude'' with the real application if the two share geometric similarity, kinematic similarity and dynamic similarity. ''Similarity'' and '' ...
. Physical and chemical simulations have also direct realistic uses, rather than research uses; in chemical engineering
Chemical engineering is an engineering field which deals with the study of the operation and design of chemical plants as well as methods of improving production. Chemical engineers develop economical commercial processes to convert raw materials ...
, for example, process simulation
Process simulation is used for the design, development, analysis, and optimization of technical process of simulation of processes such as: chemical plants, chemical processes, environmental systems, power stations, complex manufacturing operati ...
s are used to give the process parameters immediately used for operating chemical plants, such as oil refineries. Simulators are also used for plant operator training. It is called Operator Training Simulator (OTS) and has been widely adopted by many industries from chemical to oil&gas and to the power industry. This created a safe and realistic virtual environment to train board operators and engineers. Mimic
In evolutionary biology, mimicry is an evolved resemblance between an organism and another object, often an organism of another species. Mimicry may evolve between different species, or between individuals of the same species. In the simples ...
is capable of providing high fidelity dynamic models of nearly all chemical plants for operator training and control system testing.
Ergonomics
Ergonomic simulation involves the analysis of virtual products or manual tasks within a virtual environment. In the engineering process, the aim of ergonomics is to develop and to improve the design of products and work environments.[Reed, M. P., Faraway, J., Chaffin, D. B., & Martin, B. J. (2006). The HUMOSIM Ergonomics Framework: A new approach to digital human simulation for ergonomic analysis. SAE Technical Paper, 01-2365] Ergonomic simulation utilizes an anthropometric virtual representation of the human, commonly referenced as a mannequin or Digital Human Models (DHMs), to mimic the postures, mechanical loads, and performance of a human operator in a simulated environment such as an airplane, automobile, or manufacturing facility. DHMs are recognized as evolving and valuable tool for performing proactive ergonomics analysis and design. The simulations employ 3D-graphics and physics-based models to animate the virtual humans. Ergonomics software uses inverse kinematics (IK) capability for posing the DHMs.simulation software
Simulation software is based on the process of modeling a real phenomenon with a set of mathematical formulas. It is, essentially, a program that allows the user to observe an operation through simulation without actually performing that operation ...
permits interactive, real-time simulation
Real-time simulation refers to a computer model of a physical system that can execute at the same rate as actual "wall clock" time. In other words, the computer model runs at the same rate as the actual physical system. For example, if a tank take ...
and evaluation through actual human input via motion capture technologies. However, motion capture for ergonomics requires expensive equipment and the creation of props to represent the environment or product.
Some applications of ergonomic simulation in include analysis of solid waste collection, disaster management tasks, interactive gaming, automotive assembly line, virtual prototyping of rehabilitation aids, and aerospace product design. Ford engineers use ergonomics simulation software to perform virtual product design reviews. Using engineering data, the simulations assist evaluation of assembly ergonomics. The company uses Siemen's Jack and Jill ergonomics simulation software in improving worker safety and efficiency, without the need to build expensive prototypes.
Finance
In finance, computer simulations are often used for scenario planning. Risk
In simple terms, risk is the possibility of something bad happening. Risk involves uncertainty about the effects/implications of an activity with respect to something that humans value (such as health, well-being, wealth, property or the environ ...
-adjusted net present value
The net present value (NPV) or net present worth (NPW) is a way of measuring the value of an asset that has cashflow by adding up the present value of all the future cash flows that asset will generate. The present value of a cash flow depends on ...
, for example, is computed from well-defined but not always known (or fixed) inputs. By imitating the performance of the project under evaluation, simulation can provide a distribution of NPV over a range of discount rates and other variables. Simulations are also often used to test a financial theory or the ability of a financial model.
Simulations are frequently used in financial training to engage participants in experiencing various historical as well as fictional situations. There are stock market simulations, portfolio simulations, risk management simulations or models and forex simulations. Such simulations are typically based on stochastic asset model
A stochastic investment model tries to forecast how returns and prices on different assets or asset classes, (e. g. equities or bonds) vary over time. Stochastic models are not applied for making point estimation rather interval estimation and th ...
s. Using these simulations in a training program allows for the application of theory into a something akin to real life. As with other industries, the use of simulations can be technology or case-study driven.
Flight
 Flight simulation is mainly used to train pilots outside of the aircraft.
Flight simulation is mainly used to train pilots outside of the aircraft.instrument approach
In aviation, an instrument approach or instrument approach procedure (IAP) is a series of predetermined maneuvers for the orderly transfer of an aircraft operating under instrument flight rules from the beginning of the initial approach to a lan ...
es in the actual aircraft may require significant time spent repositioning the aircraft, while in a simulation, as soon as one approach has been completed, the instructor can immediately reposition the simulated aircraft to a location from which the next approach can be begun.
Flight simulation also provides an economic advantage over training in an actual aircraft. Once fuel, maintenance, and insurance costs are taken into account, the operating costs of an FSTD are usually substantially lower than the operating costs of the simulated aircraft. For some large transport category airplanes, the operating costs may be several times lower for the FSTD than the actual aircraft. Another advantage is reduced environmental impact, as simulators don't contribute directly to carbon or noise emissions.
There also exist "engineering flight simulators" which are a key element of the aircraft design process
The aircraft design process is a loosely defined method used to balance many competing and demanding requirements to produce an aircraft that is strong, lightweight, economical and can carry an adequate payload while being sufficiently reliable to ...
.
Marine
 Bearing resemblance to
Bearing resemblance to flight simulator
A flight simulator is a device that artificially re-creates aircraft flight and the environment in which it flies, for pilot training, design, or other purposes. It includes replicating the equations that govern how aircraft fly, how they rea ...
s, a marine simulator is meant for training of ship personnel. The most common marine simulators include:GMDSS
The Global Maritime Distress and Safety System (GMDSS) is a worldwide system for automated emergency signal communication for ships at sea developed by the United Nations' International Maritime Organization (IMO) as part of the SOLAS Convention. ...
simulators
* ROV simulators
Simulators like these are mostly used within maritime colleges, training institutions, and navies. They often consist of a replication of a ships' bridge, with the operating console(s), and a number of screens on which the virtual surroundings are projected.
Military
Military simulations, also known informally as war games, are models in which theories of warfare can be tested and refined without the need for actual hostilities. They exist in many different forms, with varying degrees of realism. In recent times, their scope has widened to include not only military but also political and social factors (for example, the Nationlab series of strategic exercises in Latin America). While many governments make use of simulation, both individually and collaboratively, little is known about the model's specifics outside professional circles.
Network and distributed systems
Network and distributed systems have been extensively simulated in other to understand the impact of new protocols and algorithms before their deployment in the actual systems. The simulation can focus on different levels (physical layer
In the seven-layer OSI model of computer networking, the physical layer or layer 1 is the first and lowest layer: the layer most closely associated with the physical connection between devices. The physical layer provides an electrical, mechani ...
, network layer
In the seven-layer OSI model of computer networking, the network layer is layer 3. The network layer is responsible for packet forwarding including routing through intermediate Router (computing), routers.
Functions
The network layer provides t ...
, application layer
An application layer is an abstraction layer that specifies the shared communication protocols and interface methods used by hosts in a communications network. An ''application layer'' abstraction is specified in both the Internet Protocol Su ...
), and evaluate different metrics (network bandwidth, resource consumption, service time, dropped packets, system availability). Examples of simulation scenarios of network and distributed systems are:
* Content delivery network
A content delivery network (CDN) or content distribution network is a geographically distributed network of proxy servers and their data centers. The goal is to provide high availability and performance ("speed") by distributing the service spat ...
s
* Smart cities
* Internet of things
Payment and securities settlement system
Simulation techniques have also been applied to payment and securities settlement systems. Among the main users are central banks who are generally responsible for the oversight of market infrastructure and entitled to contribute to the smooth functioning of the payment systems.
Central banks have been using payment system simulations to evaluate things such as the adequacy or sufficiency of liquidity available ( in the form of account balances and intraday credit limits) to participants (mainly banks) to allow efficient settlement of payments. The need for liquidity is also dependent on the availability and the type of netting procedures in the systems, thus some of the studies have a focus on system comparisons.
Another application is to evaluate risks related to events such as communication network breakdowns or the inability of participants to send payments (e.g. in case of possible bank failure). This kind of analysis falls under the concepts of stress testing
Stress testing is a form of deliberately intense or thorough testing, used to determine the stability of a given system, critical infrastructure or entity. It involves testing beyond normal operational capacity, often to a breaking point, in orde ...
or scenario analysis
Scenario planning, scenario thinking, scenario analysis, scenario prediction and the scenario method all describe a strategic planning method that some organizations use to make flexible long-term plans. It is in large part an adaptation and gen ...
.
A common way to conduct these simulations is to replicate the settlement logics of the real payment or securities settlement systems under analysis and then use real observed payment data. In case of system comparison or system development, naturally, also the other settlement logics need to be implemented.
To perform stress testing and scenario analysis, the observed data needs to be altered, e.g. some payments delayed or removed. To analyze the levels of liquidity, initial liquidity levels are varied. System comparisons (benchmarking) or evaluations of new netting algorithms or rules are performed by running simulations with a fixed set of data and varying only the system setups.
An inference is usually done by comparing the benchmark simulation results to the results of altered simulation setups by comparing indicators such as unsettled transactions or settlement delays.
Power systems
Project management
Project management simulation is simulation used for project management training and analysis. It is often used as a training simulation for project managers. In other cases, it is used for what-if analysis and for supporting decision-making in real projects. Frequently the simulation is conducted using software tools.
Robotics
A robotics simulator is used to create embedded applications for a specific (or not) robot without being dependent on the 'real' robot. In some cases, these applications can be transferred to the real robot (or rebuilt) without modifications. Robotics simulators allow reproducing situations that cannot be 'created' in the real world because of cost, time, or the 'uniqueness' of a resource. A simulator also allows fast robot prototyping. Many robot simulators feature physics engine
A physics engine is computer software that provides an approximate simulation of certain physical systems, typically classical dynamics, including rigid body dynamics (including collision detection), soft body dynamics, and fluid dynamics. I ...
s to simulate a robot's dynamics.
Production
Simulation of production systems is used mainly to examine the effect of improvements or investments in a production system Production system may refer to:
* Computer Animation Production System (CAPS), developed by the Walt Disney Company and Pixar in the 1980s
* Production system (computer science), a program used to provide some form of artificial intelligence
* Pro ...
. Most often this is done using a static spreadsheet with process times and transportation times. For more sophisticated simulations Discrete Event Simulation
A discrete-event simulation (DES) models the operation of a system as a (discrete) sequence of events in time. Each event occurs at a particular instant in time and marks a change of state in the system. Between consecutive events, no change in th ...
(DES) is used with the advantages to simulate dynamics in the production system. A production system is very much dynamic depending on variations in manufacturing processes, assembly times, machine set-ups, breaks, breakdowns and small stoppages. There is much software
Software consists of computer programs that instruct the Execution (computing), execution of a computer. Software also includes design documents and specifications.
The history of software is closely tied to the development of digital comput ...
commonly used for discrete event simulation. They differ in usability and markets but do often share the same foundation.
Sales process
Simulations are useful in modeling the flow of transactions through business processes, such as in the field of sales process engineering
Sales process engineering is the systematic design of sales processes done in order to make sales more effective and efficient..
It can be applied in functions including sales, marketing, and customer service
Customer service is the assista ...
, to study and improve the flow of customer orders through various stages of completion (say, from an initial proposal for providing goods/services through order acceptance and installation). Such simulations can help predict the impact of how improvements in methods might impact variability, cost, labor time, and the number of transactions at various stages in the process. A full-featured computerized process simulator can be used to depict such models, as can simpler educational demonstrations using spreadsheet software, pennies being transferred between cups based on the roll of a die, or dipping into a tub of colored beads with a scoop.
Sports
In sports, computer simulation
Computer simulation is the running of a mathematical model on a computer, the model being designed to represent the behaviour of, or the outcome of, a real-world or physical system. The reliability of some mathematical models can be determin ...
s are often done to predict the outcome of events and the performance of individual sportspeople. They attempt to recreate the event through models built from statistics. The increase in technology has allowed anyone with knowledge of programming the ability to run simulations of their models. The simulations are built from a series of mathematical algorithms
In mathematics and computer science, an algorithm () is a finite sequence of mathematically rigorous instructions, typically used to solve a class of specific problems or to perform a computation. Algorithms are used as specifications for per ...
, or models, and can vary with accuracy. Accuscore, which is licensed by companies such as ESPN
ESPN (an initialism of their original name, which was the Entertainment and Sports Programming Network) is an American international basic cable sports channel owned by the Walt Disney Company (80% and operational control) and Hearst Commu ...
, is a well-known simulation program for all major sports
Sport is a physical activity or game, often competitive and organized, that maintains or improves physical ability and skills. Sport may provide enjoyment to participants and entertainment to spectators. The number of participants in ...
. It offers a detailed analysis of games through simulated betting lines, projected point totals and overall probabilities.
With the increased interest in fantasy sports
A fantasy sport (also known less commonly as rotisserie or roto) is a game, often played using the internet, where participants assemble imaginary or virtual teams composed of proxies of real players of a professional sport. These teams compete ba ...
simulation models that predict individual player performance have gained popularity. Companies like What If Sports and StatFox specialize in not only using their simulations for predicting game results but how well individual players will do as well. Many people use models to determine whom to start in their fantasy leagues.
Another way simulations are helping the sports field is in the use of biomechanics
Biomechanics is the study of the structure, function and motion of the mechanical aspects of biological systems, at any level from whole organisms to Organ (anatomy), organs, Cell (biology), cells and cell organelles, using the methods of mechani ...
. Models are derived and simulations are run from data received from sensors attached to athletes and video equipment. Sports biomechanics Sports biomechanics is the quantitative based study and analysis of athletes and sports activities in general. It can simply be described as the physics of sports. Within this specialized field of biomechanics, the laws of mechanics are applied in o ...
aided by simulation models answer questions regarding training techniques such as the effect of fatigue on throwing performance (height of throw) and biomechanical factors of the upper limbs (reactive strength index; hand contact time).
Computer simulations allow their users to take models which before were too complex to run, and give them answers. Simulations have proven to be some of the best insights into both play performance and team predictability.
Space shuttle countdown
 Simulation was used at
Simulation was used at Kennedy Space Center
The John F. Kennedy Space Center (KSC, originally known as the NASA Launch Operations Center), located on Merritt Island, Florida, is one of the NASA, National Aeronautics and Space Administration's (NASA) ten NASA facilities#List of field c ...
(KSC) to train and certify Space Shuttle
The Space Shuttle is a retired, partially reusable launch system, reusable low Earth orbital spacecraft system operated from 1981 to 2011 by the U.S. National Aeronautics and Space Administration (NASA) as part of the Space Shuttle program. ...
engineers during simulated launch countdown operations. The Space Shuttle engineering community would participate in a launch countdown integrated simulation before each Shuttle flight. This simulation is a virtual simulation where real people interact with simulated Space Shuttle vehicle and Ground Support Equipment (GSE) hardware. The Shuttle Final Countdown Phase Simulation, also known as S0044, involved countdown processes that would integrate many of the Space Shuttle vehicle and GSE systems. Some of the Shuttle systems integrated in the simulation are the main propulsion system, RS-25
The RS-25, also known as the Space Shuttle Main Engine (SSME), is a liquid-fuel cryogenic rocket engine that was used on NASA's Space Shuttle and is used on the Space Launch System.
Designed and manufactured in the United States by Rocketd ...
, solid rocket boosters
A solid rocket booster (SRB) is a solid propellant motor used to provide thrust in spacecraft launches from initial launch through the first ascent. Many launch vehicles, including the Atlas V, SLS and Space Shuttle, have used SRBs to give launch ...
, ground liquid hydrogen and liquid oxygen, external tank
The Space Shuttle external tank (ET) was the component of the Space Shuttle launch vehicle that contained the liquid hydrogen Rocket propellant, fuel and liquid oxygen oxidizer. During lift-off and ascent it supplied the fuel and oxidizer und ...
, flight controls, navigation, and avionics. The high-level objectives of the Shuttle Final Countdown Phase Simulation are:
* To demonstrate firing room
Firing may refer to:
* Dismissal (employment), sudden loss of employment by termination
* Firemaking, the act of starting a fire
* Burning; see combustion
* Shooting, specifically the discharge of firearms
* Execution by firing squad, a method of ...
final countdown phase operations.
* To provide training for system engineers in recognizing, reporting and evaluating system problems in a time critical environment.
* To exercise the launch team's ability to evaluate, prioritize and respond to problems in an integrated manner within a time critical environment.
* To provide procedures to be used in performing failure/recovery testing of the operations performed in the final countdown phase.
The Shuttle Final Countdown Phase Simulation took place at the Kennedy Space Center
The John F. Kennedy Space Center (KSC, originally known as the NASA Launch Operations Center), located on Merritt Island, Florida, is one of the NASA, National Aeronautics and Space Administration's (NASA) ten NASA facilities#List of field c ...
Launch Control Center
The Rocco A. Petrone Launch Control Center (commonly known as just the Launch Control Center or LCC) is a four-story building at NASA's Kennedy Space Center on Merritt Island, Florida, used to manage rocket launch, launches of launch vehicles from ...
firing rooms. The firing room used during the simulation is the same control room where real launch countdown operations are executed. As a result, equipment used for real launch countdown operations is engaged. Command and control computers, application software, engineering plotting and trending tools, launch countdown procedure documents, launch commit criteria documents, hardware requirement documents, and any other items used by the engineering launch countdown teams during real launch countdown operations are used during the simulation.
The Space Shuttle vehicle hardware and related GSE hardware is simulated by mathematical models
A mathematical model is an abstract description of a concrete system using mathematical concepts and language. The process of developing a mathematical model is termed ''mathematical modeling''. Mathematical models are used in applied mathemati ...
(written in Shuttle Ground Operations Simulator (SGOS) modeling language) that behave and react like real hardware. During the Shuttle Final Countdown Phase Simulation, engineers command and control hardware via real application software executing in the control consoles – just as if they were commanding real vehicle hardware. However, these real software applications do not interface with real Shuttle hardware during simulations. Instead, the applications interface with mathematical model representations of the vehicle and GSE hardware. Consequently, the simulations bypass sensitive and even dangerous mechanisms while providing engineering measurements detailing how the hardware would have reacted. Since these math models interact with the command and control application software, models and simulations are also used to debug and verify the functionality of application software.
Satellite navigation
The only true way to test GNSS
A satellite navigation or satnav system is a system that uses satellites to provide autonomous geopositioning. A satellite navigation system with global coverage is termed global navigation satellite system (GNSS). , four global systems are op ...
receivers (commonly known as Sat-Nav's in the commercial world) is by using an RF Constellation Simulator. A receiver that may, for example, be used on an aircraft, can be tested under dynamic conditions without the need to take it on a real flight. The test conditions can be repeated exactly, and there is full control over all the test parameters. this is not possible in the 'real-world' using the actual signals. For testing receivers that will use the new Galileo (satellite navigation)
Galileo is a satellite navigation, global navigation satellite system (GNSS) created by the European Union through the European Space Agency (ESA) and operated by the European Union Agency for the Space Programme (EUSPA). It is headquartered ...
there is no alternative, as the real signals do not yet exist.
Trains
Weather
Predicting weather conditions by extrapolating/interpolating previous data is one of the real use of simulation. Most of the weather forecasts use this information published by Weather bureaus. This kind of simulations helps in predicting and forewarning about extreme weather conditions like the path of an active hurricane/cyclone. Numerical weather prediction
Numerical weather prediction (NWP) uses mathematical models of the atmosphere and oceans to weather forecasting, predict the weather based on current weather conditions. Though first attempted in the 1920s, it was not until the advent of comput ...
for forecasting involves complicated numeric computer models to predict weather accurately by taking many parameters into account.
Simulation games
Strategy game
A strategy game or strategic game is a game in which the players' uncoerced, and often autonomous, decision-making skills have a high significance in determining the outcome. Almost all strategy games require internal decision tree-style think ...
s—both traditional and modern—may be viewed as simulations of abstracted decision-making for the purpose of training military and political leaders (see History of Go
History is the systematic study of the past, focusing primarily on the human past. As an academic discipline, it analyses and interprets evidence to construct narratives about what happened and explain why it happened. Some theorists categ ...
for an example of such a tradition, or Kriegsspiel
''Kriegsspiel'' is a genre of wargaming developed by the Prussian Army in the 19th century to teach battlefield tactics to officers. The word ''Kriegsspiel'' literally means "wargame" in German, but in the context of the English language it ref ...
for a more recent example).
Many other video games are simulators of some kind. Such games can simulate various aspects of reality, from business
Business is the practice of making one's living or making money by producing or Trade, buying and selling Product (business), products (such as goods and Service (economics), services). It is also "any activity or enterprise entered into for ...
, to government
A government is the system or group of people governing an organized community, generally a State (polity), state.
In the case of its broad associative definition, government normally consists of legislature, executive (government), execu ...
, to construction
Construction are processes involved in delivering buildings, infrastructure, industrial facilities, and associated activities through to the end of their life. It typically starts with planning, financing, and design that continues until the a ...
, to piloting vehicles (see above).
Historical usage
Historically, the word had negative connotations:
However, the connection between simulation and dissembling
A lie is an assertion that is believed to be false, typically used with the purpose of deception, deceiving or misleading someone. The practice of communicating lies is called lying. A person who communicates a lie may be termed a liar. Lies ...
later faded out and is now only of linguistic interest.[South, in the passage quoted, was speaking of the differences between a falsehood and an honestly mistaken statement; the difference being that for the statement to be a ]lie
A lie is an assertion that is believed to be false, typically used with the purpose of deceiving or misleading someone. The practice of communicating lies is called lying. A person who communicates a lie may be termed a liar. Lies can be int ...
the truth
Truth or verity is the Property (philosophy), property of being in accord with fact or reality.Merriam-Webster's Online Dictionarytruth, 2005 In everyday language, it is typically ascribed to things that aim to represent reality or otherwise cor ...
must be known, and the opposite of the truth must have been knowingly uttered. And, from this, to the extent to which a ''lie'' involves deceptive ''words'', a ''simulation'' involves deceptive ''actions'', deceptive ''gestures'', or deceptive ''behavior''. Thus, it would seem, if a simulation is ''false'', then the truth must be known (for ''something other than the truth'' to be presented in its stead); and, for the ''simulation'' to ''simulate''. Because, otherwise, one would not know what to offer up in a simulation. Bacon's essay '' Of Simulation and Dissimulation'' expresses somewhat similar views. Samuel Johnson
Samuel Johnson ( – 13 December 1784), often called Dr Johnson, was an English writer who made lasting contributions as a poet, playwright, essayist, moralist, literary critic, sermonist, biographer, editor, and lexicographer. The ''Oxford ...
thought so highly of South's definition, that he used it in the entry for simulation in his '' Dictionary of the English Language''.
See also
* Computer experiment
A computer experiment or simulation experiment is an experiment used to study a computer simulation, also referred to as an in silico system. This area includes computational physics, computational chemistry, computational biology and other simila ...
* Grey box model
* ''In silico
In biology and other experimental sciences, an ''in silico'' experiment is one performed on a computer or via computer simulation software. The phrase is pseudo-Latin for 'in silicon' (correct ), referring to silicon in computer chips. It was c ...
''
* List of computer simulation software
The following is a list of notable computer simulation software.
Free or open-source
* Advanced Simulation Library - open-source hardware accelerated multiphysics simulation software.
* ASCEND - open-source equation-based modelling environme ...
* List of discrete event simulation software
This is a list of notable discrete-event simulation software.
Commercial
Open source
See also
* List of computer-aided engineering software
This is a list of notable computer-aided engineering software.
See also
* Computational fl ...
* Merger simulation Merger simulation is a commonly used technique when analyzing potential welfare costs and benefits of mergers between firms. Merger simulation models differ with respect to assumed form of competition that best describes the market (e.g. differenti ...
* Microarchitecture simulation
Microarchitecture simulation is an important technique in computer architecture research and computer science education. It is a tool for modeling the design and behavior of a microprocessor and its components, such as the Arithmetic logic unit, AL ...
* Mining simulator
A mining simulator is a type of simulation used for entertainment as well as in training purposes for mining companies. These simulators replicate elements of real-world mining operations on surrounding screens displaying three-dimensional imag ...
* Monte Carlo algorithm
In computing, a Monte Carlo algorithm is a randomized algorithm whose output may be incorrect with a certain (typically small) probability. Two examples of such algorithms are the Karger–Stein algorithm and the Monte Carlo algorithm for mini ...
* Network simulation
In computer network research, network simulation is a technique whereby a software program replicates the behavior of a real network. This is achieved by calculating the interactions between the different network entities such as routers, switc ...
* Pharmacokinetics simulation
* Roleplay simulation
Roleplay simulation is an experiential learning method in which either amateur or professional roleplayers (also called interactors) improvise with learners as part of a simulated scenario. Roleplay is designed primarily to build first-person exp ...
* Rule-based modeling
Rule-based modeling is a modeling approach that uses a set of rules that indirectly specifies a mathematical model. The rule-set can either be translated into a model such as Markov chains or differential equations, or be treated using tools tha ...
* Simulated reality
A simulated reality is an approximation of reality created in a simulation, usually in a set of circumstances in which something is engineered to appear real when it is not.
Most concepts invoking a simulated reality relate to some form of compu ...
* Simulation language
A computer simulation language is used to describe the operation of a simulation on a computer.Fritzson, Peter, and Vadim Engelson.Modelica—A unified object-oriented language for system modeling and simulation" European Conference on Object-Orie ...
* Training simulation
In business, training simulation (also known as Simulation-based training) is a virtual medium through which various types of skills can be acquired. Training simulations can be used in a variety of genres; however they are most commonly used in c ...
* Web-based simulation Web-based simulation (WBS) is the invocation of computer simulation services over the World Wide Web, specifically through a web browser. Increasingly, the web is being looked upon as an environment for providing modeling and simulation applications ...
* Virtual reality
Virtual reality (VR) is a Simulation, simulated experience that employs 3D near-eye displays and pose tracking to give the user an immersive feel of a virtual world. Applications of virtual reality include entertainment (particularly video gam ...
* Simulation hypothesis
The simulation hypothesis proposes that what one experiences as the real world is actually a simulated reality, such as a computer simulation in which humans are constructs. There has been much debate over this topic in the Philosophy, philosophi ...
Fields of study
* Computational astrophysics
Computational astrophysics refers to the methods and computing tools developed and used in astrophysics research. Like computational chemistry or computational physics, it is both a specific branch of theoretical astrophysics and an interdiscip ...
* Computational chemistry
Computational chemistry is a branch of chemistry that uses computer simulations to assist in solving chemical problems. It uses methods of theoretical chemistry incorporated into computer programs to calculate the structures and properties of mol ...
* Computational fluid dynamics
Computational fluid dynamics (CFD) is a branch of fluid mechanics that uses numerical analysis and data structures to analyze and solve problems that involve fluid dynamics, fluid flows. Computers are used to perform the calculations required ...
* Computational physics
Computational physics is the study and implementation of numerical analysis to solve problems in physics. Historically, computational physics was the first application of modern computers in science, and is now a subset of computational science ...
* Futures studies
Futures studies, futures research or futurology is the systematic, interdisciplinary and holistic study of social and technological advancement, and other environmental trends, often for the purpose of exploring how people will live and wor ...
* Molecular dynamics
Molecular dynamics (MD) is a computer simulation method for analyzing the Motion (physics), physical movements of atoms and molecules. The atoms and molecules are allowed to interact for a fixed period of time, giving a view of the dynamics ( ...
* System identification
The field of system identification uses statistical methods to build mathematical models of dynamical systems from measured data. System identification also includes the optimal design#System identification and stochastic approximation, optimal de ...
Specific examples & literature
* Illustris project
The Illustris project is an ongoing series of astrophysical simulations run by an international collaboration of scientists. The aim is to study the processes of galaxy formation and evolution in the universe with a comprehensive physical model. ...
* Planet Simulator
* UltraHLE
UltraHLE is a discontinued emulator for the Nintendo 64. Emulating the Nintendo 64 (which was only three years old at the time) made it the first of the N64 emulators to run commercial titles at a playable frame rate on the hardware of the tim ...
* Simulacra and Simulation
''Simulacra and Simulation'' () is a 1981 philosophical treatise by the philosopher and cultural theorist Jean Baudrillard, in which he seeks to examine the relationships between reality, symbols, and society, in particular the significations ...
References
External links
Bibliographies containing more references
to be found on the website of the journa
''Simulation & Gaming''
{{Authority control
Mathematical and quantitative methods (economics)

 Historically, simulations used in different fields developed largely independently, but 20th-century studies of
Historically, simulations used in different fields developed largely independently, but 20th-century studies of  There is a wide variety of input hardware available to accept user input for virtual simulations. The following list briefly describes several of them:
* ''Body tracking'': The
There is a wide variety of input hardware available to accept user input for virtual simulations. The following list briefly describes several of them:
* ''Body tracking'': The  Flight simulation is mainly used to train pilots outside of the aircraft. In comparison to training in flight, simulation-based training allows for practicing maneuvers or situations that may be impractical (or even dangerous) to perform in the aircraft while keeping the pilot and instructor in a relatively low-risk environment on the ground. For example, electrical system failures, instrument failures, hydraulic system failures, and even flight control failures can be simulated without risk to the crew or equipment.
Instructors can also provide students with a higher concentration of training tasks in a given period of time than is usually possible in the aircraft. For example, conducting multiple
Flight simulation is mainly used to train pilots outside of the aircraft. In comparison to training in flight, simulation-based training allows for practicing maneuvers or situations that may be impractical (or even dangerous) to perform in the aircraft while keeping the pilot and instructor in a relatively low-risk environment on the ground. For example, electrical system failures, instrument failures, hydraulic system failures, and even flight control failures can be simulated without risk to the crew or equipment.
Instructors can also provide students with a higher concentration of training tasks in a given period of time than is usually possible in the aircraft. For example, conducting multiple  Bearing resemblance to
Bearing resemblance to  Simulation was used at
Simulation was used at